基于多基因遗传编程的凝析气藏露点压力估算方法

黄鑫 ，张芮菡 ，张烈辉 ，鲁友常 ，袁山 ，敬晓锋

（1.油气藏地质及开发工程国家重点实验室，四川 成都 610500；2.四川页岩气勘探开发有限责任公司，四川 成都 610041；3.中国石油西南油气田公司勘探开发研究院，四川 成都 610041；4.中国石油玉门油田分公司勘探开发研究院，甘肃酒泉735000）

0 引言

凝析气藏开发过程中，烃类流体的相态变化影响凝析气藏开发政策的制定，而准确预测凝析气藏露点压力是研究相态变化、调整开发政策的重要依据[1-4]。高于露点压力开发凝析气藏时，气藏储层流动为单相流动；低于露点压力开发时，饱和凝析气中的凝析油析出，气藏储层流动由单相流变为两相流。凝析油的析出带来两方面的改变：一是析出的凝析油占据渗流孔道，降低气相渗透率，加大了储层敏感性，改变了储层渗流环境，增加了储层开发难度[5-7]；二是凝析油的析出引起凝析气藏资源量的巨大损失，达到50%～70%[8]，大大降低了凝析气藏的采收率，造成天然气和凝析油双重资源上的损失。因此，建立合理可靠的凝析气藏露点压力计算方法，降低气藏反凝析损失，对凝析气藏高效开发有着重要意义。

目前国内外关于露点压力的计算可以分为室内实验法、状态方程法和经验公式法：1）室内实验法主要采用 PVT实验进行等组分膨胀（CCE）[9-10]和定容衰竭（CVD）[11-13]确定露点压力。实验过程中，地层流体测试样品需要进行复配重组，存在人为误差，容易造成样本数据失真，且实验测试费用昂贵，耗时较长，结果的准确性依赖样本数量和质量[14]。PVT实验过程中忽略了地层条件多孔介质界面效应的影响，也使得室内测试结果存在一定的偏差[15]。2）状态方程法是通过联立物质平衡方程和压降方程，推导出凝析气藏视地层压力和凝析气累计产量之间的关系式，根据2段斜率不同的直线交点确定露点压力。常用方法包括Peng-Robinson 状态方程[16]、Soave 状态方程[17]和 LHHSS 状态方程[18]。但状态方程法在预测过程中受限于不同馏分的劈分方式和表征方法[19]，露点压力的计算数值因状态方程和参数的选择不同而并不唯一[20-21]。3）经验公式法早期利用大量实验数据、组分数据等相关参数，通过多元回归方法建立经验方程[19，22]，产生相关系数，并需要大量的数据支持，对预测模型的数据来源和研究方法有较强的依赖。目前常用的研究方法包括机器学习领域中的神经网络[23-24]、遗传算法[25-26]、粒子群算法[27]、支持向量机技术[28-29]等。

以上3种方法均存在各自的局限性：室内实验法测试时间长，数据解释样本依赖性较强；状态方程法结构复杂，求解繁琐，存在半理论、半经验参数；经验公式法集合了目前非线性模型预测求解方法，但样本需求量大和隐式模型结构的缺点使得矿场快速应用存在障碍。由于强非线性关系及影响参数的不确定性等原因，需要开发出鲁棒性更好的理论工具来解决模型预测中的问题。生产过程中积累了大量的数据，利用数据驱动反演模型的思想建立“数据-模型-数据”耦合对应的显式模型，更有利于油田现场的便捷使用[30]。本文在多基因遗传编程理论[31]的基础上，选取储层温度、流体组分和实测露点压力为样本变量组建数据库，提出了一种凝析气藏露点压力显式模型计算方法。该方法可以利用单井级别数据进行小样本预测，也可以针对油田级大数据进行大样本预测，通过非线性模型回归出具有实际参数意义的显式数学模型。

1 多基因遗传编程基本原理

多基因遗传编程（MGGP）是遗传编程（GP）的一个变体[31]。这种算法是在遗传算法的基础上仿照自然界生物进化机制，通过模仿进化过程寻找用户指定任务的最优解，目前广泛应用于非线性模型的开发数据驱动[32]。与GP相比，MGGP可以使用训练数据集自动开发显式模型，无需事前定义模型结构。这样不仅可以促进数学模型的开发，还可以避免因受某些主观判断，尤其是有关模型结构的判断而导致的误差。MGGP主要具有两方面的优势：1）MGGP模型中的每个基因都是传统的GP基因，因此MGGP更加准确；2）每个MGGP基因只需要包含几个树深，因此每个基因中非线性项的阶数较低，MGGP通常更加紧凑。图1展示了利用MGGP方法进行模型进化的基本原理。

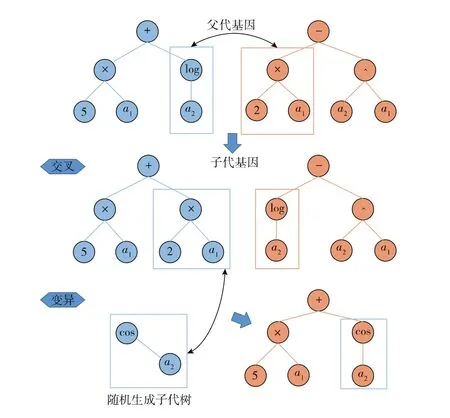
图1 MGGP子树层结构及进化过程示意

父代基因中随机生成2个基因（Gene1-1，Gene2-1），其数学表达式分别为

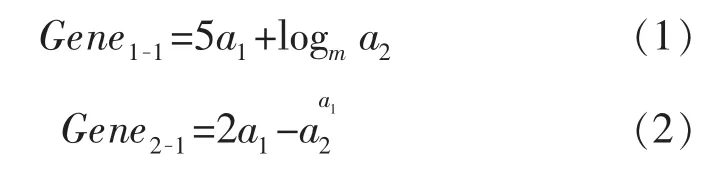
式中：a1，a2为模型输入参数；m为系统自动拟合底数。

由父代基因生成的模型适应性通常很差，在对数据的拟合方面误差较高，MGGP方法通过3种基本遗传算子（选择、交叉和变异），控制父代基因生成子代基因，在随机扰动情况下控制群体中的个体基因向最优解迁移。交叉父代基因（Gene1-1，Gene2-1）生成子代基因（Gene1-2，Gene2-2），其数学表达式分别为

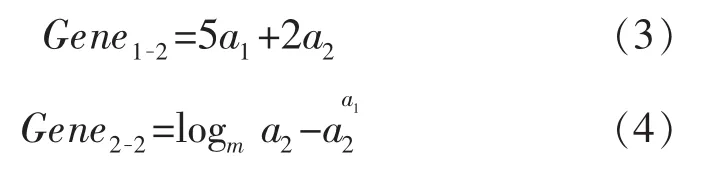
在基因突变过程中，Gene1-2中的子树被新元素所替代，通过基因变异产生子代基因（Gene1-3），其数学表达式为

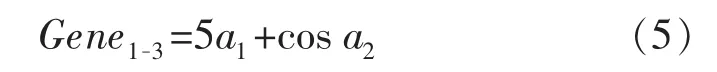
新生成的基因通过线性组合的方式即可生成基于MGGP的显性模型表达式。针对图1中的实例，显性模型的函数表达式为

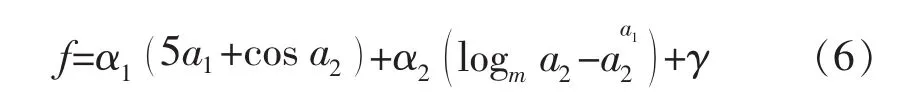
式中：α1，α2分别为 Gene1-3和 Gene2-2的权重系数；γ 为偏差。

选取均方根误差RMSE和决定系数R2作为模型的适应度函数进行模型性能评估：

式中：N为样本数量；i为样本序号；下标A，P，M分别表示实际值、预测值和平均值。

2 模型建立与求解

2.1 模型建立

取气藏温度 T、C1的摩尔分数 n（C1）、C2—6的摩尔分数 n（C2—6）、C7+的摩尔分数 n（C7+）、C7+的相对密度 Γ（C7+）、C7+的相对分子质量 M（C7+）等 6 个参数[33]作为模型自变量，分别用x1—x6表示；选取气藏露点压力pdew作为因变量，用y表示。选取文献[34]中给出的27组凝析气藏露点压力实测数据（见表1），构建基于MGGP的气藏露点压力计算原始数据库。

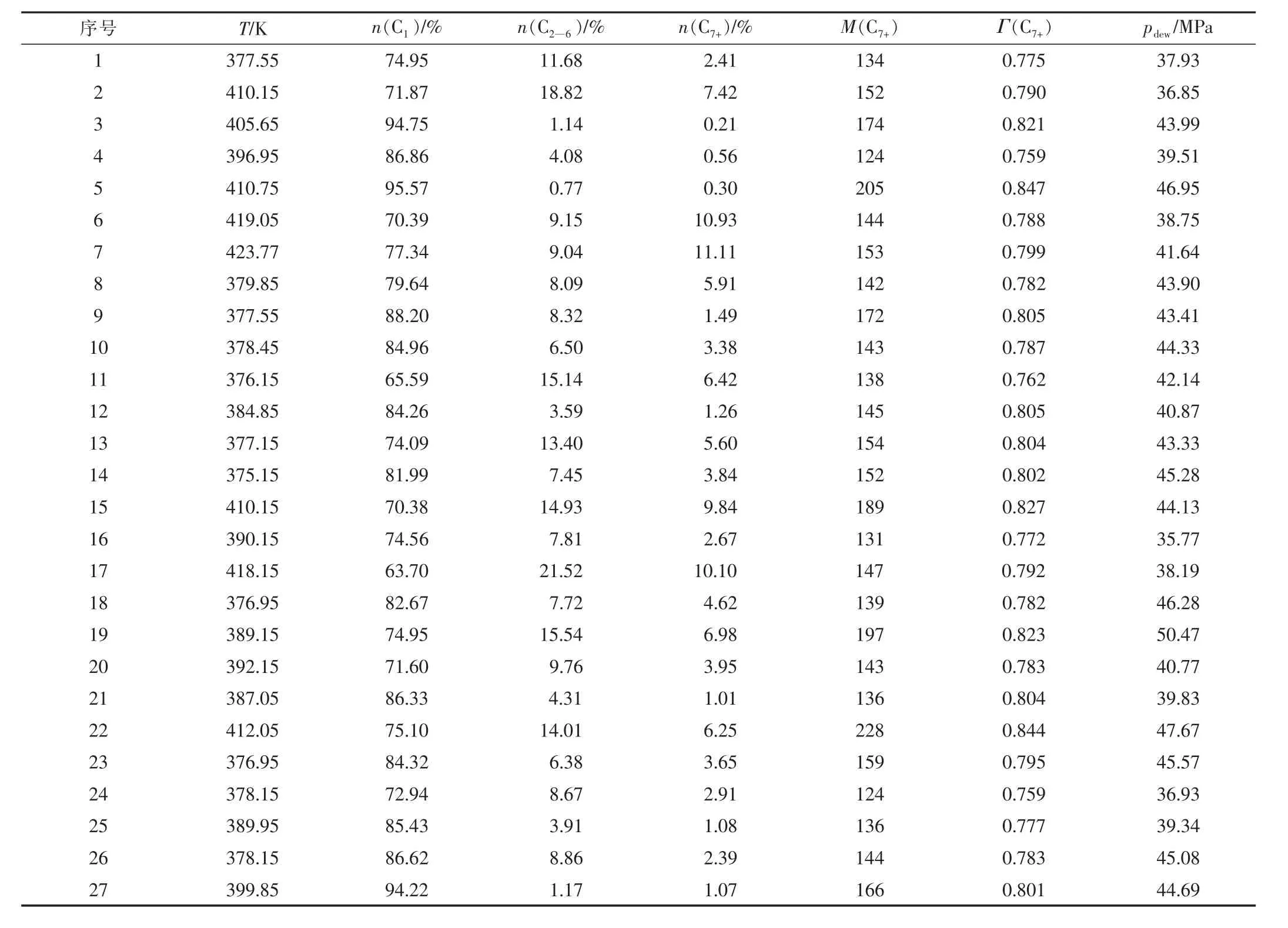
表1 凝析气藏露点压力测试数据

基于MGGP的凝析气藏露点压力计算过程在MATLAB环境下编程运行[35]。初始种群总数设置为500，最大生成代数为200，基因最大树深和最大基因数分别设置为3和5，交叉概率、遗传概率和变异概率分别为0.84，0.30，0.14。函数集是描述自变量和因变量之间函数关系的集合，本文函数集包括×，-，+，/，^，sin，cos，tan，tanh，log，exp 等。

将27组数据随机分为训练组和预测组，训练组包括20组数据，预测组包括7组数据。基于MGGP的凝析气藏露点压力预测模型计算流程如图2所示。

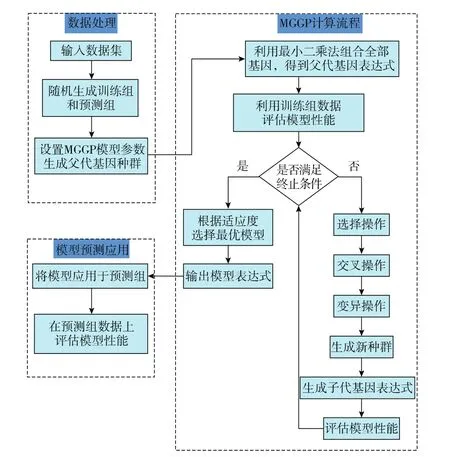
图2 基于MGGP的露点压力预测模型建模步骤

2.2 模型结果分析

图3为基于MGGP生成的子代模型及模型收敛情况。图3a中所有的点为基于MGGP模型通过27组数据“锻炼”生成的预测模型，确定子代最佳模型需要同时考虑预测精度和模型复杂度两方面。1-R2的值越小，表示预测精度越高；绿色点表示生成的模型中的非支配解，即不会同时存在一个最精确、最简单的解。计算结果给出了13个非支配解，其中A模型为所有预测模型中推荐的最优模型。为了与最优模型作比较，在13个非支配解中选择B模型和C模型与最优模型A进行对比分析。

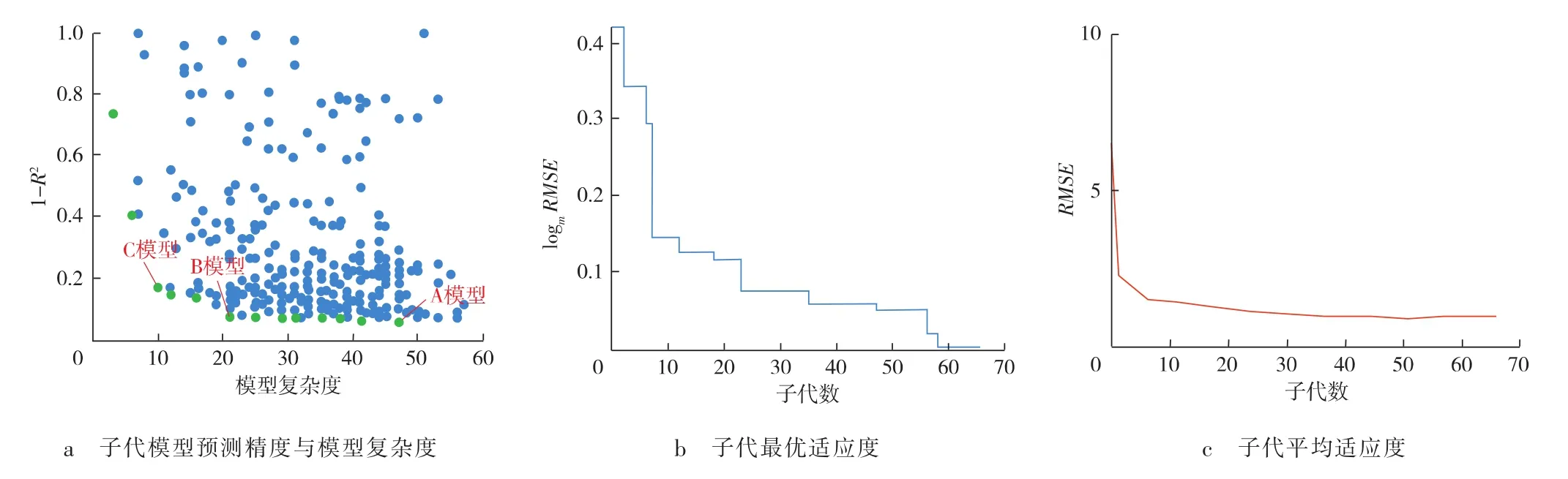
图3 基于MGGP生成的子代模型及模型收敛情况

图3b，3c表示种群在进化生成子代模型过程中子代适应度的收敛性。从图中可以看出：在模型演化开始，模型性能相对较差，随着子代数量的增加，RMSE迅速降低；迭代到20代之后，RMSE已经收敛到可接受的范围。

演化生成的子代模型通用表达式为

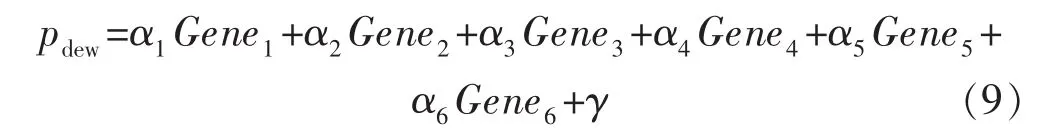
式中：α为基因在数学模型中的权重系数；下标数字表示基因序号。

表2给出了A，B，C 3个模型基因项的表达式（偏差项分别为13，72，71）。从表2可以看出，A模型由6个基因组成，是3个模型中复杂度最高的。这些通过选择、交叉和变异的遗传过程建立的模型，相比传统的数据统计回归生成的数学模型，能更加有效地检测出变量之间的隐藏关系，具有更好的适应性。

表2 基于MGGP生成的预测模型基因项数学表达式

A，B，C 3个模型训练组和预测组与实际数据的拟合情况见图4，而图5反映了训练组和预测组数据的线性相关性。

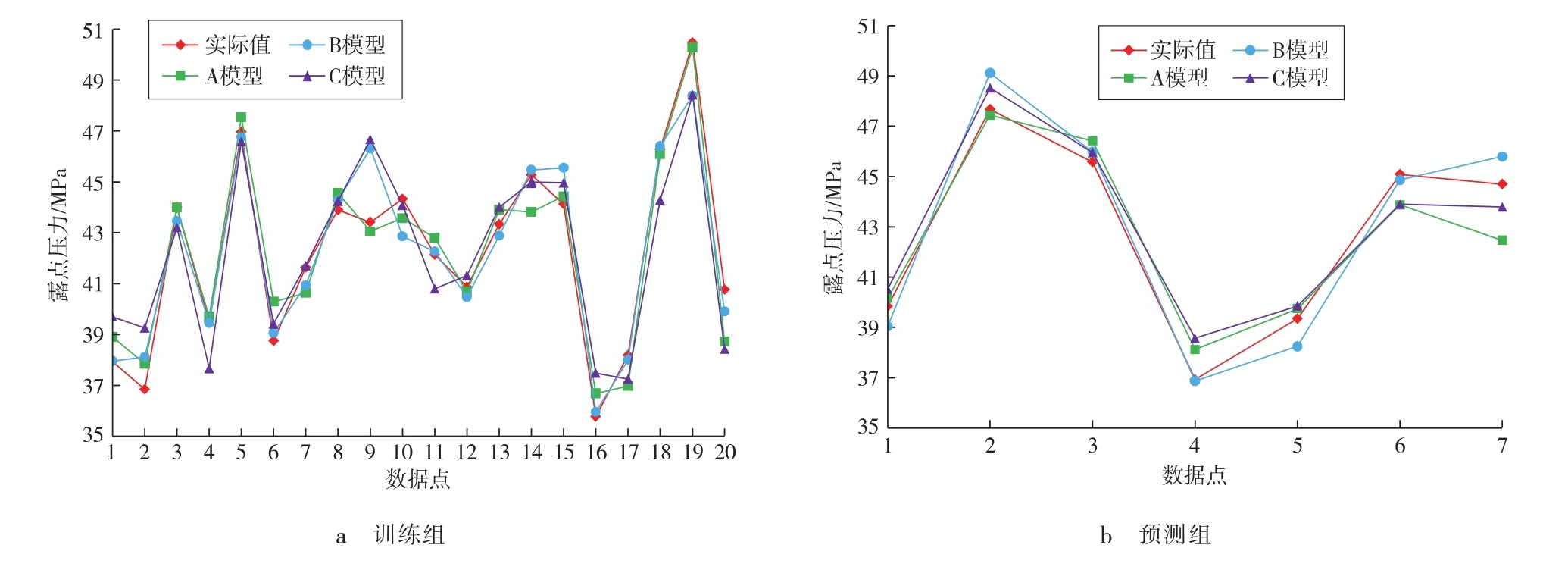
图4 基于MGGP生成的模型训练组、预测组与实测数据模拟结果

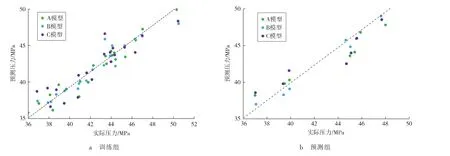
图5 基于MGGP生成的模型训练组、预测组对照散点图

由图4、图5可以看出：1）B模型的训练精度（R2=0.920）大于A模型（R2=0.905），且 B模型预测组的预测精度（R2=0.944）也要高于A模型（R2=0.937）。如果非常看重模型的复杂度，那么B模型要优于A模型，这就表明数据过度拟合带来了较大的风险，因此，在生成模型时要着重控制生成代数，避免数据的过度拟合。2）C模型在基因数量上要少于A模型和B模型，模型的复杂度也较低，从C模型的训练精度（R2=0.827）和预测精度（R2=0.892）上也可以反映出模型的训练不足给模型的开发方面带来了较大的不稳定性。3）A，B模型的预测组误差均小于7%，而C模型的预测组误差达到10%左右，性能较差。

通过上述分析可以发现，A模型和B模型均可用于凝析气藏露点压力的预测。若模型的复杂度是考虑的首要因素，则B模型是最优选择，但是A模型在模型复杂度和预测误差两方面均具有较好的泛化能力，因此，采用A模型进行凝析气藏露点压力的计算。

对表1中27组实测露点压力数据进行降序排列，采用Matlab中非线性回归预测置信区间函数nlpredci进行分析。图6是基于MGGP生成的A模型置信区间分析情况。从图6可以看出，A模型的预测结果很好地遵循了总体数据的分布趋势，露点压力数据在A模型预测曲线±95%的置信区间半宽内分布，表明A模型预测结果和实际数据之间具有良好的置信度。

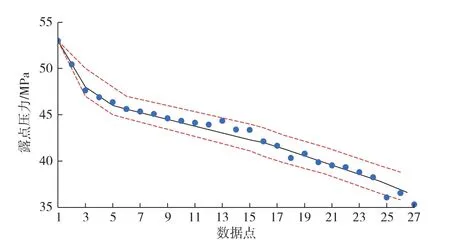
图6 A模型置信区间分析

3 模型验证

为了验证基于MGGP生成的模型的预测能力，选用文献[36]中给出的塔里木油田不同凝析气井露点压力测试数据，用A模型对15组现场数据进行拟合，计算露点压力。结果见图7、表3。由图7可看出，预测值和实际值比较吻合，最大预测误差为7.99%，最小预测误差为1.15%，平均预测误差为4.36%。结果表明，基于MGGP方法建立的凝析气藏露点压力预测模型具有良好的矿场适应性，可以快速进行露点压力预测。

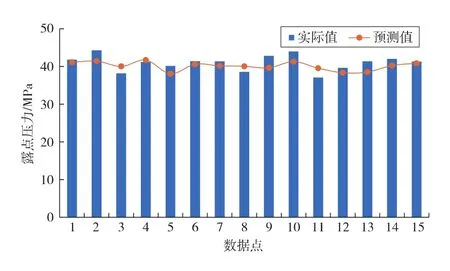
图7 A模型预测值与实际值对比

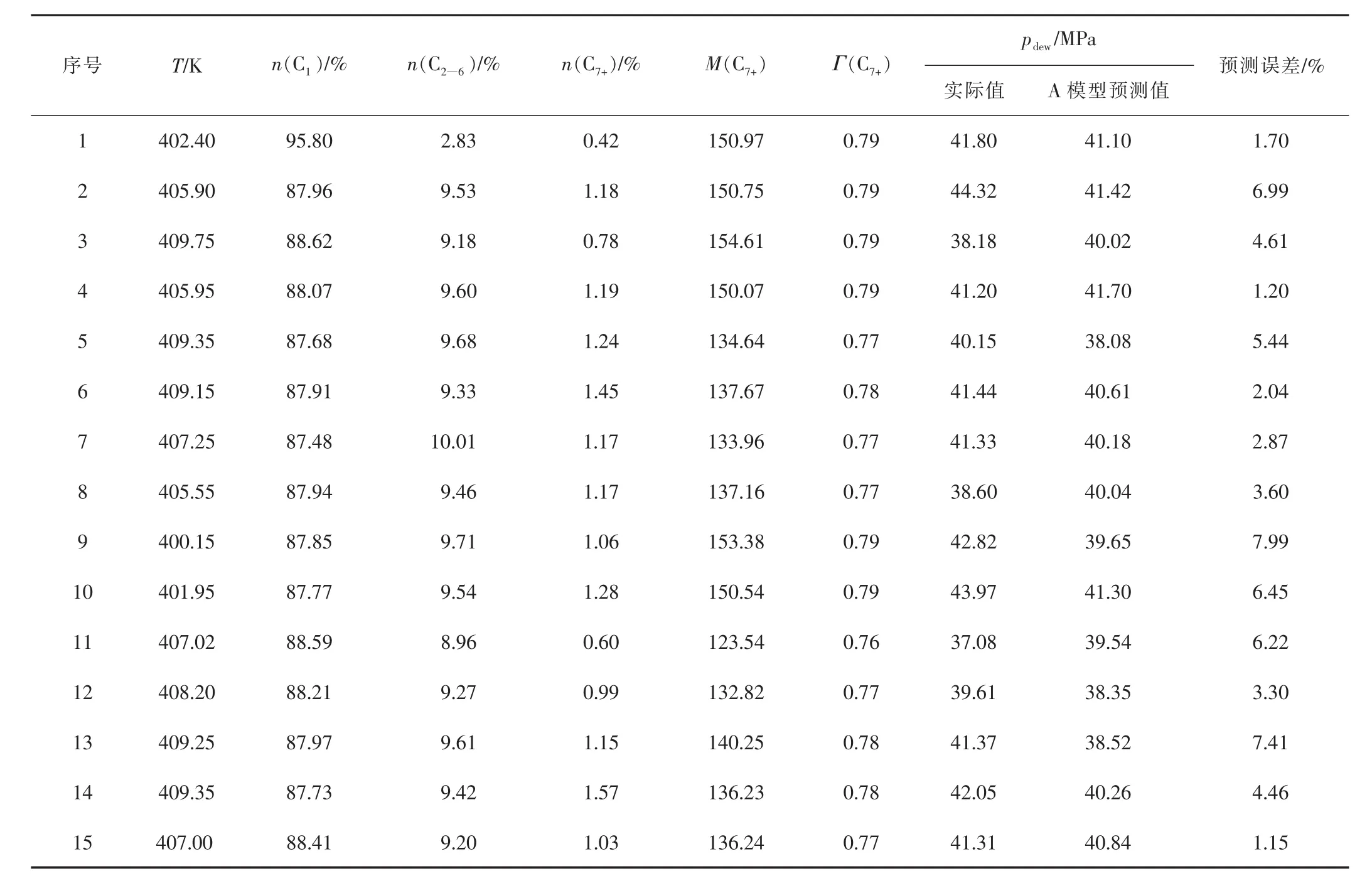
表3 不同凝析气井露点压力测试数据及预测数据

4 结论

1）基于多基因遗传编程的露点压力计算方法能够快速高效地建立显式数学模型，模型中不含经验参数，生成的数学模型具有良好的泛化能力和鲁棒性。

2）选用储层温度、流体组分和露点压力等7个参数，针对实际矿场数据“锻炼”生成数学模型，依据预测精度和模型复杂度可优选出适合实际矿场需要的数学模型，且过拟合预测风险较低。

3）利用优选出的数学模型对公开发表的矿场实际数据进行预测，预测结果表明，预测值和实际值最大误差为7.99%，最小误差为1.15%，平均误差为4.36%，预测精度满足现场使用条件。