基于测井数据的页岩可压性定量评价
杨宏伟,李军,柳贡慧,2,李玉梅,席岩,唐庚
(1.中国石油大学(北京)石油工程学院,北京 102249;2.北京工业大学机械工程与应用电子学院,北京100192;3.中国石油西南油气田分公司工程技术研究院,四川 广汉 618300)
基于测井数据的页岩可压性定量评价
杨宏伟1,李军1,柳贡慧1,2,李玉梅1,席岩1,唐庚3
(1.中国石油大学(北京)石油工程学院,北京 102249;2.北京工业大学机械工程与应用电子学院,北京100192;3.中国石油西南油气田分公司工程技术研究院,四川 广汉 618300)
可压性是指在压裂过程中页岩发生有效破裂的能力。目前对可压性的研究主要基于定性评价,或建立在岩石力学实验和压裂施工参数基础上的定量评价,难以完整连续地表征非均质性较强的页岩在水平井长水平段的可压性变化。基于测井数据,评价了页岩脆性指数、脆性矿物质量分数、断裂韧性、黏土矿物质量分数和总有机碳质量分数对可压性的影响,并利用层次分析法和模糊数学法,从定性和定量相结合的角度建立了页岩长水平段的连续可压性数学模型,且划分了可压性级别。该模型将可压性划分为3个级别:当可压性指数高于0.48时,页岩的可压性好;当可压性为0.32~0.48时,页岩的可压性中等;当可压性低于0.32时,页岩的可压性较差。研究表明,利用测井数据能够更全面细致地评价沿水平井长水平段的页岩可压性,对压裂设计和射孔参数设计具有更好的指导性。现场应用表明,该模型能够较准确连续地预测页岩可压性,且具有广泛的适用性。
页岩水平井;可压性数学模型;测井数据;层次分析法;模糊数学法
可压性是指在压裂过程中页岩发生有效破裂的能力,决定了压裂后裂缝的形态及裂缝网络的复杂程度,是储层改造体积的重要影响因素之一[1]。国外学者最早通过脆性指数来表征可压性,为可压性的定量评价提供了思路,但研究因素较单一[2-5]。随着研究的深入,M.J.Mullen,X.C.Jin等[6-7]基于岩石力学实验和压裂施工参数建立了不同的可压性定量评价方法;袁俊良、侯冰、唐颖等[1,8-9]利用岩石力学实验、页岩体积压裂评价和工程技术评价等,探索了页岩可压性评价体系。由于页岩在水平井长水平段的非均质性较强,这些方法难以完整、连续地表征页岩可压性在长水平段的具体变化,不能合理地指导水力压裂设计和射孔参数设计。本文基于测井数据来评价页岩脆性指数、脆性矿物质量分数、断裂韧性、黏土矿物质量分数、总有机碳质量分数(TOC)对可压性的影响,建立了页岩水平井长水平段的连续可压性数学模型,并对可压性级别进行划分,为水力压裂设计和射孔参数设计提供了理论依据。
1 页岩可压性影响因素评价
1.1 脆性指数
页岩脆性指数是可压性最重要的影响因素,主要通过弹性模量和泊松比来定量表征。弹性模量越大,泊松比越小,页岩脆性指数越大,可压性越好。目前,脆性指数的计算方法通常是采用Rickman等[3]提出的计算模型(见式(1))。利用声波测井数据可计算动态弹性参数,然后转换为静态弹性参数,进而计算页岩脆性指数。

式中:BI为脆性指数;YMBI为归一化的弹性模量;PRBI为归一化的泊松比;YMSC为静态弹性模量,10 GPa;PRC为静态泊松比。
1.2 脆性矿物和黏土矿物质量分数
脆性矿物和黏土矿物质量分数是影响页岩基质孔隙、微裂缝发育程度及含气性等的重要因素,决定了裂缝的发育形态,反映了页岩在水力压裂时形成复杂缝网体的能力[10]。脆性矿物质量分数越高,黏土矿物质量分数越低,越容易形成复杂缝网体。利用元素俘获能谱测井(ECS)数据可以较精确地分析页岩中石英、长石、碳酸盐岩、黄铁矿、黏土等矿物成分的质量分数[11]。
1.3 断裂韧性
断裂韧性是表征页岩储层压裂难易程度的重要因素,反映了压裂过程中裂缝形成之后维持裂缝向前延伸的能力[12]。水力裂缝主要是Ⅰ,Ⅱ型裂缝或者Ⅰ,Ⅱ型的复合型裂缝。金衍[13-14]基于力学实验和测井数据,建立了利用测井资料预测岩石Ⅰ型和Ⅱ型断裂韧性的数学模型:
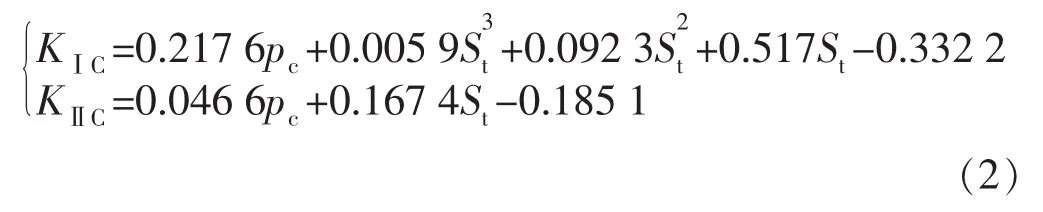
式中:KⅠC,KⅡC分别为Ⅰ型和Ⅱ型裂缝的断裂韧度,MPa·m1/2;pc为围压,MPa;St为岩石抗拉强度,MPa。
1.4 总有机碳质量分数
总有机碳质量分数反映的是页岩储层中有机质的质量分数和生烃能力,由于其并不能直接反映裂缝的起裂能力及扩展能力,在以往的可压性研究中常被忽略。路菁[15]依据岩石天然放射性差异,利用自然伽马能谱测井的总伽马与去铀伽马曲线重叠来识别富含有机碳井段,进而结合钍铀比(V(Th)/V(U)),建立了定量评价不同沉积环境页岩TOC的方法。该方法计算简单,精度也较高,计算式为
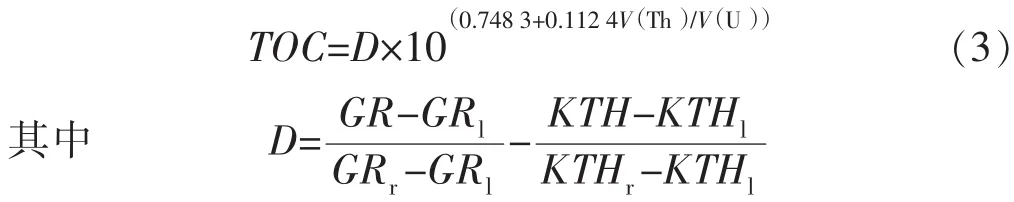
式中:D为GR与KTH两曲线的分离度;GR与KTH分别为自然伽马能谱测井的总伽马值与去铀伽马值,API;GRl,GRr分别为GR-KTH曲线重叠时GR曲线左、右刻度,API;KTHl,KTHr分别为GR-KTH曲线重叠时KTH曲线左、右刻度,API。
1.5 其他因素
可压性的影响因素还包括黏聚力、内摩擦角、天然裂缝和地应力差等。根据以往的研究经验,断裂韧性相比于黏聚力能更全面的反映可压性程度,而内摩擦角与脆性指数的影响规律相似;天然裂缝越发育的页岩储层可压性越好,但是天然裂缝在页岩储层中随机分布,且裂缝检测技术不完善,准确描述天然裂缝十分困难;地应力差在同一深度的页岩储层中变化不大,主要通过选择合理的射孔簇参数或压裂措施,减弱水平地应力差或使水平地应力发生反转,从而在压裂时形成较好的裂缝网络系统。所以,本文进行可压性定量评价时暂不考虑以上4种因素。
2 可压性综合评价模型的建立
水平井长水平段页岩非均质性较强,难以直接建立一种可压性与水平段长度、影响因素之间的确定关系。根据其他领域研究经验,利用层次分析法结合模糊数学法,建立水平井长水平段页岩可压性定量评价模型。
2.1 层次分析法确定可压性影响因素的权重
2.1.1 判断矩阵的建立
利用层次分析法分析问题时,首先需要将问题层次化,构造一个有层次的结构模型。根据页岩可压性与其影响因素的关系,建立结构模型(见图1)。

图1 页岩储层可压性影响因素层次结构
判断矩阵表示某一层的元素之间相对于上一层元素的重要性程度,可以利用1—9的比例标度来表示这种重要性程度[16](见表1)。
根据以往学者对可压性的研究,将可压性影响因素进行两两比较,可得判断矩阵A,如表2所示。
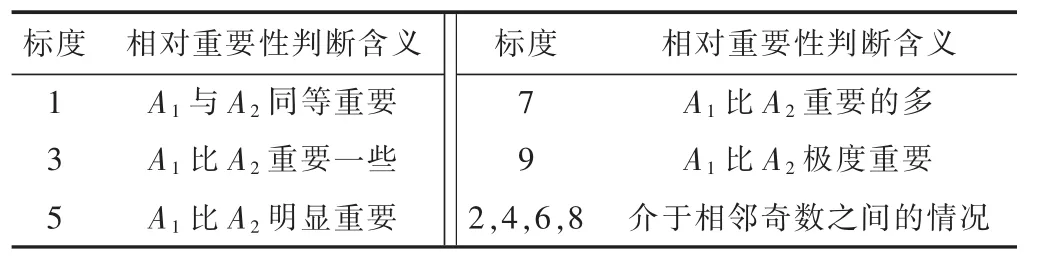
表1 标度及其含义
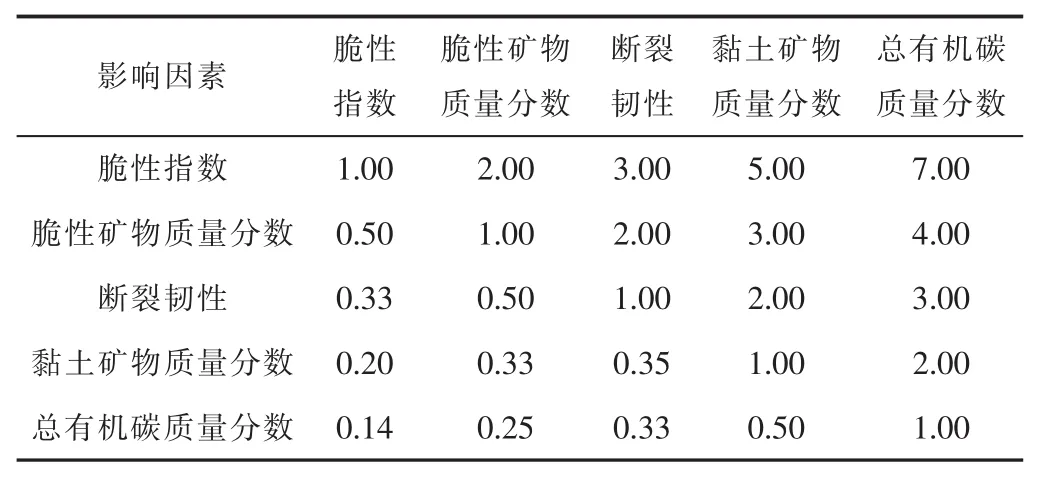
表2 判断矩阵A
2.1.2 权重向量的计算
利用和积法计算判断矩阵A的最大特征根及其对应的特征向量,从而确定可压性各影响因素的权重:
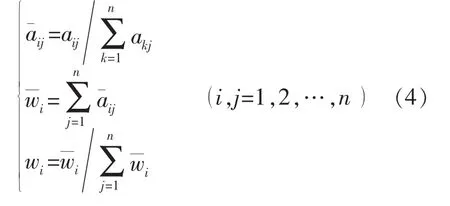
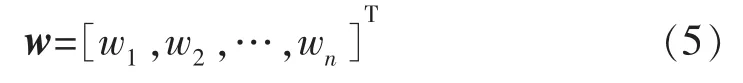
式中:aij为判断矩阵A的元素;w为所求的特征向量(即各个元素的权重值)。
可得 w=[0.45,0.25,0.15,0.09,0.06]T,即为所求的特征向量,即脆性指数、脆性矿物质量分数,断裂韧性、黏土矿物质量分数和TOC对应的权重值分别为0.45,0.25,0.15,0.09,0.06。
为了防止可压性影响因素之间存在自相矛盾,必须对判断矩阵A进行一致性检验。经检验,该判断矩阵A符合一致性要求。
2.2 模糊数学法确定可压性影响因素的模糊矩阵
2.2.1 因素集的建立
根据可压性评价目标,建立因素集:
U={脆性指数,脆性矿物质量分数,断裂韧性,黏土矿物质量分数,TOC}。
2.2.2 评价集的建立
选择页岩水平井水平段不同井深作为评价对象,定量评价不同井深页岩可压性的相对大小。评价集是评价对象出现各种可能的集合,可压性的评价集为V={井深1,井深2,井深3,…,井深m}。
2.2.3 隶属度的计算
由于可压性各影响因素之间的单位、量纲、数值范围均不同,为便于比较,需将各参数进行归一化处理。页岩的脆性指数、脆性矿物质量分数、TOC越大,页岩的可压性越好,与可压性呈正相关;而断裂韧性和黏土矿物质量分数越低,可压性越好,与可压性呈负相关。
对于正向指标进行归一化处理,取:

对于负向指标进行归一化处理,取:

式中:S为参数标准化值;X为参数值;Xmax为参数最大值;Xmin为参数最小值。
极值变换后,正、负向指标均化为正向指标,最优值为1,最劣值为0。
将归一化后的结果作为隶属度,因素集中第n个元素对评价集中第m个元素的隶属度表示为Rmn,以此建立模糊矩阵R(见表3)。
2.3 可压性综合评价数学模型的建立
为了全面评价长水平段不同井深处的页岩可压性,在单因素评价的基础上,将层次分析法和模糊数学法相结合,建立一个综合反映多因素影响下的不同井深处页岩可压性相对大小的数学模型,即:

式(8)即为可压性定量评价模型。FI为综合评价结果,反映了长水平段不同井深处页岩可压性的相对大小,亦可定义为可压性指数。可压性指数越大,可压性越好。式(8)的页岩可压性数学模型具有广泛适用性,可以在各个页岩气区块的水平井进行可压性评价时使用。

表3 由因素集和评价集元素构成的模糊矩阵R
3 页岩可压性级别划分
上述模型的计算结果只能反映长水平段不同井深处页岩可压性的相对大小,还不能直接确定页岩的可压性级别。通过对国内多个页岩气区块的水平井进行可压性计算,并将计算结果与压裂后的实际生产状况对比分析,可将页岩可压性划分为3个级别:当可压性指数高于0.48时,页岩的可压性好,压裂时容易形成好的裂缝网络,属于优质的页岩储层;当可压性指数为0.32~0.48时,页岩的可压性中等,压裂时需要采用黏度较小的压裂液或控制较高的缝内净压力,才能形成较好的裂缝网络;当可压性指数低于0.32时,页岩的可压性较差,压裂时通常不会形成理想的裂缝网络,且压裂后裂缝容易闭合,是较差的页岩储层。
4 实例分析
以四川盆地某口页岩气水平井H井为例。利用该井的测井资料,并采用上述模型分析其长水平段页岩储层的可压性。为避免数据量过大,以每50 m的间隔在长水平段上取点,并利用获取的测井数据计算每一井深对应储层的脆性指数、脆性矿物质量分数、断裂韧性、黏土矿物质量分数和TOC,然后对计算结果归一化,可得模糊矩阵R(见表4)。
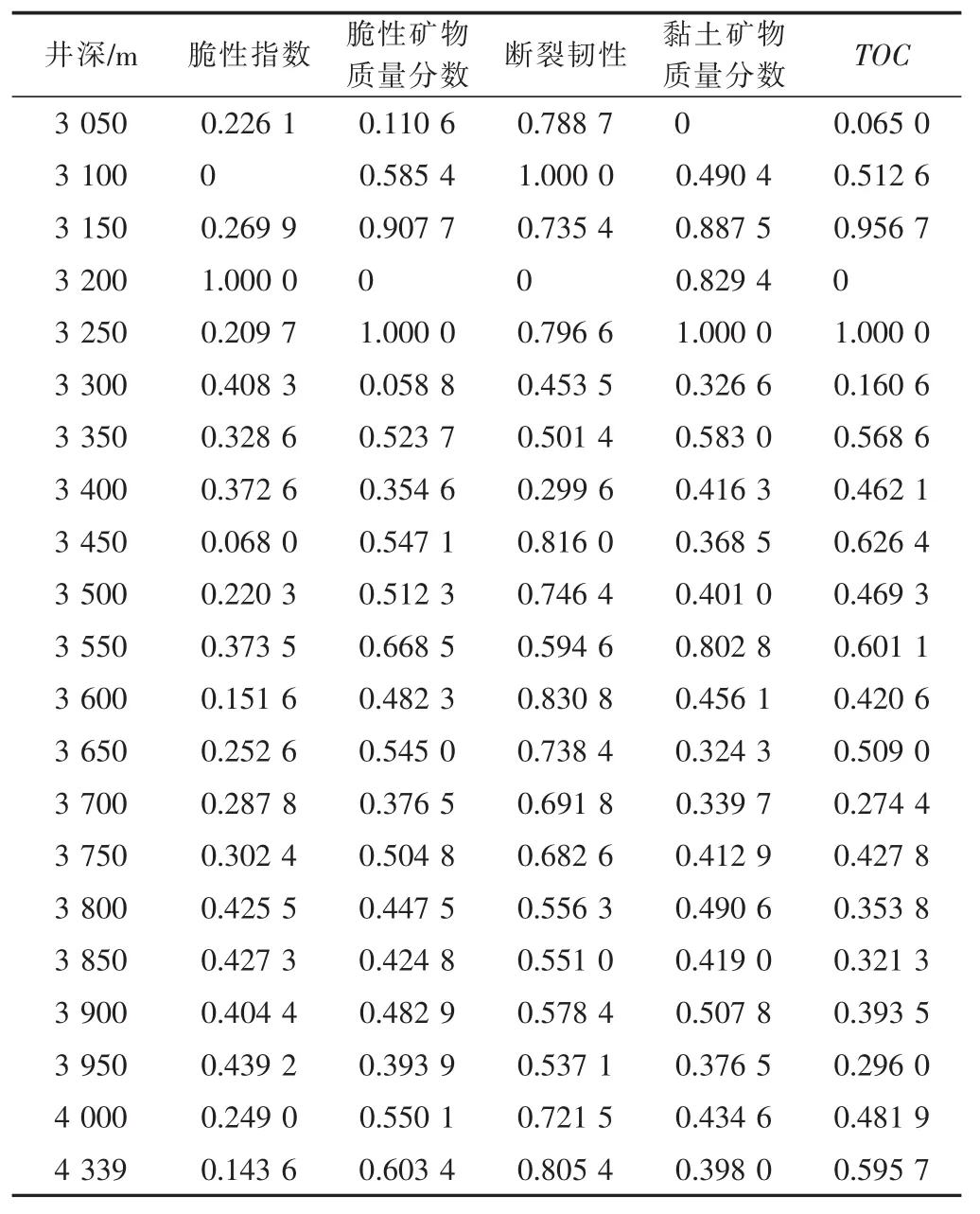
表4 H井长水平段可压性各影响因素值归一化后模糊矩阵
将模糊矩阵代入式(8),可得到页岩储层长水平段每一井深对应的页岩储层的可压性指数,即:

根据计算结果,绘制可压性沿水平段井深的变化曲线,如图2所示。
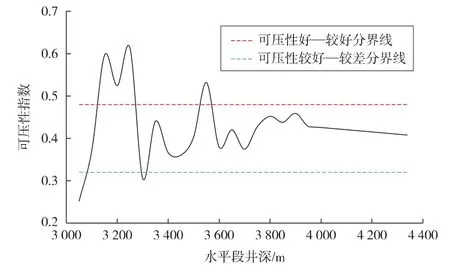
图2 H井长水平段页岩储层可压性变化曲线
图2表明,H井的可压性整体上较好,尤其在井深3 150~3 300 m,该段储层可压性指数超过0.48,是优质储层,压裂时容易形成复杂的裂缝网络系统。3 300~4 400 m范围内,页岩可压性中等,压裂时通过控制合理的压裂液排量和黏度,能够形成较好的裂缝网络。
图3为H井压裂后的微地震监测图。微地震事件点在水平面上和纵向上均有良好的分布,分布较密集,表明压裂后的效果整体较好,且距水平井跟端的裂缝网络明显好于趾端的裂缝网络。这与上述可压性数学模型预测的结果一致。
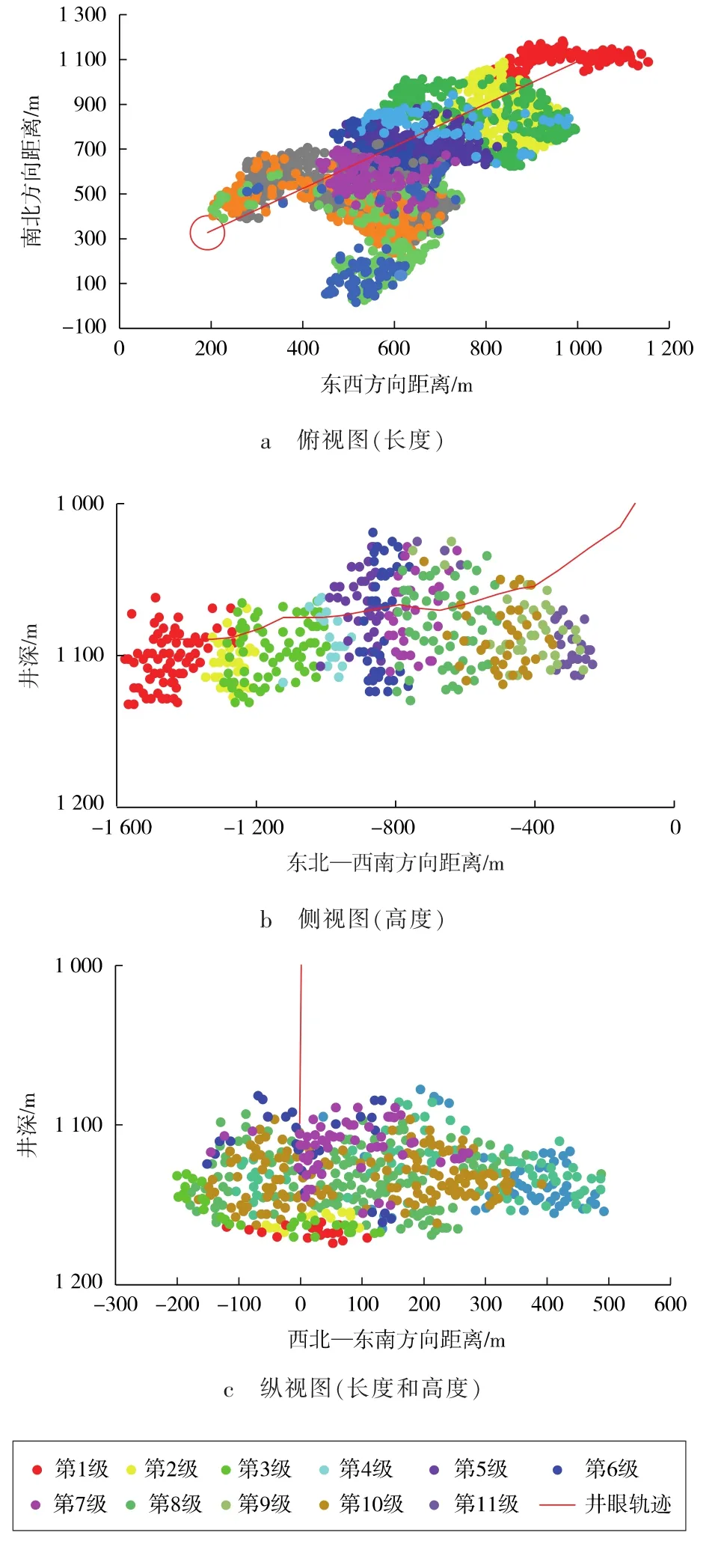
图3 H井压裂后微地震检测
5 结论
1)可压性的影响因素主要有页岩脆性、脆性矿物质量分数、断裂韧性、黏土矿物质量分数和TOC。利用层次分析法和模糊数学法,从定性和定量相结合的角度建立了连续的可压性数学模型,以表征水平段页岩可压性的相对大小。
2)运用该模型对国内多个页岩气区块的可压性计算结果与实际生产情况对比,可将可压性分为3个级别:可压性指数高于0.48,页岩可压性好,属优质页岩储层;可压性指数为0.32~0.48,页岩可压性中等,压裂后可形成较好的裂缝网络系统;可压性指数低于0.32,页岩可压性较差,是较差的页岩储层。
3)相对于岩石力学实验和现场施工参数,利用测井数据能够更全面、更细致地定量评价长水平段页岩储层的可压性,对压裂设计和射孔参数设计具有更好的指导性。现场应用效果表明,该数学模型能够准确地预测页岩储层的可压性,且该模型具有广泛的适用性,可在各个页岩气区块进行可压性评价时推广使用。
[1]袁俊亮,邓金根,张定宇,等.页岩气储层可压裂性评价技术[J].石油学报,2013,34(3):523-527.
[2]GRIESER W V,BRAY J M.Identification of production potential in unconventional reservoirs[R].SPE 106623,2007.
[3]RICKMAN R,MULLEN M J,PETRE J E,et al.A practical use of shale petrophysics for stimulation design optimization:all shale plays are not clones of the Barnett Shale[R].SPE 115258,2008.
[4]ALASSI H T,HOLT R M,NES O,et al.Realistic geomechanical modeling of hydraulic fracturing in fractured reservoir rock[R].SPE 149375,2011.
[5]KIAS E,MAHARIDGE R,HURT R.Mechanical versus mineralogical brittleness indices across various shale plays[R].SPE 174781,2015.
[6]MULLEN M J,ENDERLIN M B.Fracability index-more than just calculating rock properties[R].SPE 159755,2012.
[7]JIN X C,SHAH S N,ROEGIERS J C,et al.An integrated petrophysics and geomechanics approach for fracability evaluation in shale reservoirs[J].SPE Journal,2015,20(3):518-526.
[8]侯冰,陈勉,王凯,等.页岩储层可压性评价关键指标体系[J].石油化工高等学校学报,2014,27(6):42-49.
[9]唐颖,邢云,李乐忠,等.页岩储层可压裂性影响因素及评价方法[J].地学前缘,2012,19(5):356-363.
[10]孟召平,刘翠丽,纪懿明.煤层气/页岩气开发地质条件极其对比分析[J].煤炭学报,2013,38(5):728-736.
[11]郝建飞,周灿灿,李霞,等.页岩气地球物理测井评价综述[J].地球物理学进展,2012,27(4):1624-1632.
[12]赵金洲,许文俊,李勇明,等.页岩气储层可压性评价新方法[J].天然气地球科学,2015,26(6):1165-1172.
[13]金衍,陈勉,张旭东.利用测井资料预测深部地层岩石断裂韧性[J].岩石力学与工程学报,2001,20(4):454-456.
[14]金衍,陈勉,王怀英,等.利用测井资料预测岩石Ⅱ型断裂韧性的方法研究[J].岩石力学与工程学报,2008,27(2):3630-3635.
[15]陆菁,李军,武清钊,等.页岩油气储层有机碳含量测井评价方法研究及应用[J].科学技术与工程,2016,16(6):143-147.
[16]许树柏.实用决策方法:层次分析法原理[M].天津:天津大学出版社,1988:72.
(编辑 李宗华)
Quantitative evaluation of shale fracability based on logging data
YANG Hongwei1,LI Jun1,LIU Gonghui1,2,LI Yumei1,XI Yan1,Tang Geng3
(1.College of Petroleum Engineering,China University of Petroleum,Beijing 102249,China;2.College of Mechanical Engineering and Applied Electronics Technology,Beijing University of Technology,Beijing 100192,China;3.Engineering Technology Research Institute,Southwest Oil and Gas Field Company,PetroChina,Guanghan 618300,China)
Fracability is the capability of the shale that can be fractured effectively during fracturing process.At present,the research on the fracability is mainly through the qualitative evaluation and quantitative evaluation based on the rock mechanics test and fracturing construction parameters,which is difficult to fully characterize the variability of the shale fracability that has strong heterogeneity in horizontal wells.Based on the logging data,and by analyzing the influence of shale brittleness index,brittle mineral content,fracture toughness,clay mineral content and TOC content on the fracability and taking advantage of the analytic hierarchy process and fuzzy mathematics method,a fracability mathematical model of the long horizontal section of the shale is established by the combination of the qualitative and quantitative analysis and the level of shale fracability is divided.It is also indicated that fracability is divided into 3 levels according to this model,that is when the fracability index is higher than 0.48,shale fracability is good;when the fracability index is between 0.32 and 0.48,shale fracability is medium;when the fracability index is lower than 0.32, shale fracability is poor.The results show that the logging data can be more comprehensive and detailed to evaluate the fracability of the long horizontal interval of the shale,which provides a good guide for the design of fracturing and perforation parameter.Field application shows that the model can accurately predict the shale fracability and has a wide range of applicability.So this model can be used in the fracability evaluation of shale gas blocks.
shale horizontal well;mathematical model of fracability;logging data;analytic hierarchy process;fuzzy mathematical method
国家自然科学基金面上项目“长水平段非均质页岩储层非均匀分簇射孔优化研究”(51674272)
TE357.1+1
A
10.6056/dkyqt201703019
2016-11-28;改回日期:2017-03-12。
杨宏伟,男,1990年生,在读博士研究生,主要从事油气井岩石力学与数值模拟研究。E-mail:yhw0205@163.com。
杨宏伟,李军,柳贡慧,等.基于测井数据的页岩可压性定量评价[J].断块油气田,2017,24(3):382-386.
YANG Hongwei,LI Jun,LIU Gonghui,et al.Quantitative evaluation of shale fracability based on logging data[J].Fault-Block Oil&Gas Field,2017,24(3):382-386.

