Q960超高强钢多道焊接头残余应力的数值研究

郑 乔

(宝山钢铁股份有限公司中央研究院,上海 201999)

1 概述

随着国家碳达峰、碳中和发展战略的提出,大型重载装备的轻量化设计要求越来越高,对其关键承载部件应用超高强钢制造可以有效减轻结构重量,进而显著降低设备的运行能耗,达到节能减排的目的[1]。工程机械的生产制造离不开焊接过程,而超高强钢在焊接之后接头的性能会发生软化及脆化现象[2]。但事实上,除了性能退化问题之外,残余应力的预测和控制对超高强钢的焊接来说也非常重要,接头内部过大的残余应力会显著降低接头的疲劳性能。因此,准确预测超高强钢焊接接头残余应力,有利于灵活布置焊接接头,优化焊接结构件,提高结构件的服役寿命。但目前关于超高强钢焊接残余应力的研究报道较少。Sun[3]以S355高强钢为例,详细考虑了固态相变、加工硬化对焊接残余应力的影响,结果表明,单独考虑固态相变比加工硬化的预测准确性高,而同时考虑固态相变和加工硬化与试验结果更加吻合。

本文以Q960超高强钢为研究对象,采用模拟与试验相结合的手段,来研究Q960钢多道焊接接头的残余应力分布特征。基于有限元软件,开发了“热—冶金—力学”有限元模型。基于所开发的模型,计算多道重熔焊接接头的残余应力分布。同时,利用盲孔法测量稳定区域的残余应力分布,并与计算结果进行比较。此外,针对单道焊接头,还研究了固态相变对于焊接残余应力的分布以及大小的影响。

2 焊接试验

本试验采用的Q960超高强钢供货状态为热连轧横切板+热处理,金相组织为回火马氏体,如图1所示。焊接试件的尺寸为300 mm×200 mm×8 mm。焊前需要打磨试样表面的铁锈,同时,采用酒精清洗表面油渍。焊接时,利用非熔化极惰性气体保护焊(TIG)进行单道、两道以及四道重熔试验,详细的焊接工艺参数见表1。焊接完成后,采用盲孔法测量试样表面焊接残余应力分布,其中,应变片的布置如图2所示。

Fig.1 Q960的显微组织

图2 Q960超高强钢单道焊应变片布置

表1 焊接工艺参数

3 有限元数值模拟

本研究建立“热—冶金—力学”有限元模型,进行温度场、组织以及应力场的计算,其中,详细的计算流程如图3所示。需要注意的是,图中的虚线表示计算过程中未考虑力学计算对温度场—组织的影响。

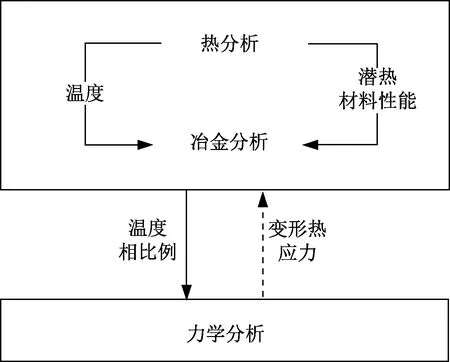
图3 热—冶金—力学耦合关系示意图

3.1 有限元模型

本研究采用“热—冶金—力学”耦合的有限元模型,模拟焊接过程中的温度场、组织含量以及残余应力分布。其中,三维有限元模型与实际焊接件的尺寸保持一致,为300 mm×200 mm×8 mm。模型中的单元总数为101 000,节点总数为112 014。数值计算时,为了平衡计算精度和效率,细化焊缝及热影响区附近的单元,最小单元尺寸为2 mm×0.5 mm×0.5 mm。为了防止模拟过程中有限元模型发生刚体位移,在三维有限元模型下表面的位置,采用三节点六自由度的拘束方式,如图4所示。

图4 三维有限元模型

3.2 热源模型

计算温度场时,采用有限元软件中提供的双椭球移动热源模型来模拟焊接过程中的熔池形态。移动热源模型的前后1/4椭球的热流密度如式(1)、(2):

(1)

(2)

式中:Qf,Qr分别为前、后1/4椭球热输入 (Qf/Qr=1.2);af,ar,b,c分别为双椭球热源模型的形状参数(af/ar=0.6)。

Q960超高强钢利用摆动TIG重熔的方式获得焊接接头,利用软件自带的热源模型无法获得与实际情况相符合的熔池形貌,因此,需要对热源模型进行修正。修正后的摆动移动热源模型和热源热流密度分布如图5[4]所示。本研究将三个并排放置的双椭球热源定义为一个摆动热源,中心热源的相对坐标系设定为(xi,yi,zi),热源在左右摆动过程中的相对坐标系设定为(xi-x0,yi,zi),(xi+x0,yi,zi),其中,x0为焊接过程中焊枪左右摆动的距离,3个热源的能量分配系数分别为η1,η2,η3,并且三者之和为1。

图5 双椭球热源模型和摆动热源热流密度分布

3.3 温度场计算

焊接是局部快速加热冷却的过程,因此,在焊接过程中,热量会在工件中传导,也会与周围的环境进行热量的交换。为了模拟实际焊接过程中电弧产生的热量在工件中的传导,其控制方程如式(3):

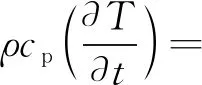
(3)

式中:ρ为材料的密度;cp为比热容;T为温度;t为时间;∇为拉普拉斯算子;qarc为焊接热源热流密度。

焊接件通过对流的方式与环境交换热量遵循Newton定律式(4):

qa=-ha(Ts-Ta)

(4)

式中:qa为焊接件与环境之间的热量交换;ha(25W·m-2·K-1)为对流交换系数;Ts为焊接件表面温度;Ta为环境温度。

焊接件通过辐射所损失的热量可按照如式(5)控制方程计算:

qh=-εσ[(Ts+273)4-(Ta+273)4]

(5)

式中:ε为热辐射系数(计算中取值为0.8);σ(5.67×10-8W·m-2·K-4)为Stefan-Boltzmanm常数。

3.4 组织计算

在焊接热循环的作用下,Q960超高强钢焊缝及热影响区的组织由奥氏体转变成贝氏体和马氏体组织。数值模拟时,奥氏体转变成贝氏体的过程,主要通过式(6)Johnson-Mehl-Avrami方程表述:

θ=θeq[1-exp(-ktn)]

(6)

式中:θeq为平衡状态下相的体积分数;k为活化率,与温度密切相关;n为Avrami指数,与相变类型有关。

奥氏体转变成马氏体的过程为非扩散型相变过程,可以通过式(7)Koistinen-Marburger方程表示:

θ=1-exp[-b(Ms-T)] (Ms≥T)

(7)

式中:b为马氏体转变速率,是与材料相关的常数;Ms为马氏体开始转变温度。

3.5 应力计算

材料的总应变包括弹性应变、热应变、塑性应变、相变塑性应变和蠕变应变。计算时,弹性行为遵守各向同性Hooke定律,屈服准则服从Von Mises准则。由于超高强钢加工硬化不显著,本文采用的计算模型为理想弹塑性模型。但是,Q960超高强钢焊后会发生贝氏体和马氏体相变,因此,必须要考虑相变塑性应变的影响。而焊接过程中,材料在高温的停留时间较短,可以忽略蠕变应变带来的影响。数值模拟时,应力场计算的应变增量表示如式(8):

Δεtotal=Δεe+Δεth+Δεpc+Δεtp

(8)

式中:Δεe为弹性应变增量;Δεpc为塑性应变增量;Δεth为热应变增量;Δεtp为相变塑性应变增量。

4 结果与讨论

4.1 有限元模型的验证

焊接过程中,摆动热源的移动,以及焊接件上瞬时状态的温度分布,见图6。其中,定义温度高于1 450 ℃的区域为熔池,730～1 450 ℃的区域为热影响区,低于730 ℃的区域为母材。图7为焊缝截面峰值温度分布与实际焊接接头的对比。由图7可知,数值模拟结果与实际焊接接头熔池形貌吻合良好,验证了有限元模型温度场计算的准确性。

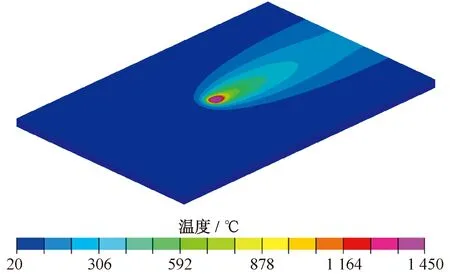
图6 焊接过程瞬时温度分布

图7 焊缝截面峰值温度分布

为了研究应力场计算的准确性,沿着图4中的直线L1,测量焊接试样上表面的残余应力分布。其中,图8为单道重熔残余应力分布的计算结果与试验值的对比。由图8可知,利用所开发的热—冶金—力学有限元模型,能够有效预测Q960超高强焊接残余应力的分布。值得注意的是,试验值与数值模拟结果存在一定的差异,主要原因是Q960数值模拟的热物理性能参数测量比较昂贵,本文所用的是普通高强钢的热物理性能参数,因此计算时相的比例存在一定误差,进而影响模拟结果。此外,残余应力测量时,试验者和设备本身都可能会造成一定的试验误差。

图8 沿L1上纵向和横向残余应力分布

4.2 焊接残余应力数值模拟结果

图9为不考虑固态相变时纵向和横向的残余应力分布。由图9(a)可知,不考虑固态相变,焊缝及热影响区域存在着较大的纵向拉伸残余应力,峰值达到1 000 MPa。而横向残余应力的数值相对较小,只有300 MPa。但是,中央截面上横向残余应力沿板厚方向上呈现“压—拉—压—拉”的分布,见图9(b)。图10(a)、(b)分别为考虑固态相变时纵向和横向的残余应力分布。由图10(a)所示,考虑固态相变时,焊缝及热影响区的纵向残余应力较低,只有300 MPa。而拉伸残余应力峰值出现在熔池底部的热影响区,峰值达到1 000 MPa。由图10(b)可知,中央截面上的横向残余应力峰值区域位于熔池底部的热影响区,且整个截面上的横向残余应力沿板厚方向上呈现“拉—压—拉—压”。

图9 不考虑固态相变时纵向和横向残余应力分布

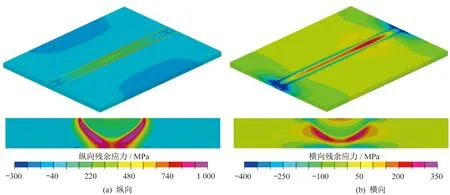
图10 考虑固态相变时纵向和横向残余应力分布

对比图9(a)和图10(a)可知,考虑固态相变能够显著降低焊缝中纵向拉伸残余应力的大小,但不能改变残余应力的正负号[5]。比较图9(b)和图10(b)可知,考虑固态相变,不但能改变横截面上横向残余应力的分布,还能使横向残余应力的峰值大小发生变化。在工程上,预测焊接接头或者结构的残余应力时,不考虑固态相变的影响所得到的残余应力值,具有一定的指导意义,但是整体结果偏保守。

图11(a)、(c)分别为两道和四道焊接纵向残余应力分布。由图11可知,高应力区域位于焊缝底部的热影响区,而焊缝中心应力数值相对比较小。随着焊道数的增加,前面焊道形成的残余应力会发生重新分布,主要表现为最后一道焊侧,平行于焊缝的端部位置的压应力逐渐增大。值得注意的是,焊缝中心的最大残余应力出现在第一道焊的焊缝中。图11(b)、(d)分别为两道和四道焊接横向残余应力分布,其中,最后一道焊缝中心的横向残余应力峰值最大,达到160 MPa。单道重熔时,见图10(b),中央截面的应力沿板厚方向上呈现出“拉—压—拉—压”;但是随着焊道数的增加,最后一道焊的横向残余应力沿板厚方向上分布为“拉—压—拉”。需要注意的是,由于几何端部效应的影响,在焊道的起始和结束位置存在着较大的横向压缩残余应力,达到-400 MPa。

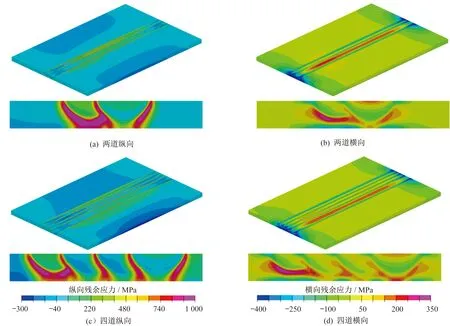
图11 两道和四道焊的残余应力分布

图12(a)和图12(c)分别为两道和四道焊中央截面上表面纵向残余应力分布,由图可知,纵向残余应力在热影响区位置出现局部拉应力峰值,而焊缝中心纵向残余应力显著下降,且焊缝中心的纵向残余应力峰值均为第一道焊缝中。图12(b)、(d)分别为两道和四道焊中央截面上表面横向残余应力分布,由图可知,焊缝中心的横向残余应力呈“阶梯上升趋势”,且在热影响区位置出现局部压应力峰值。

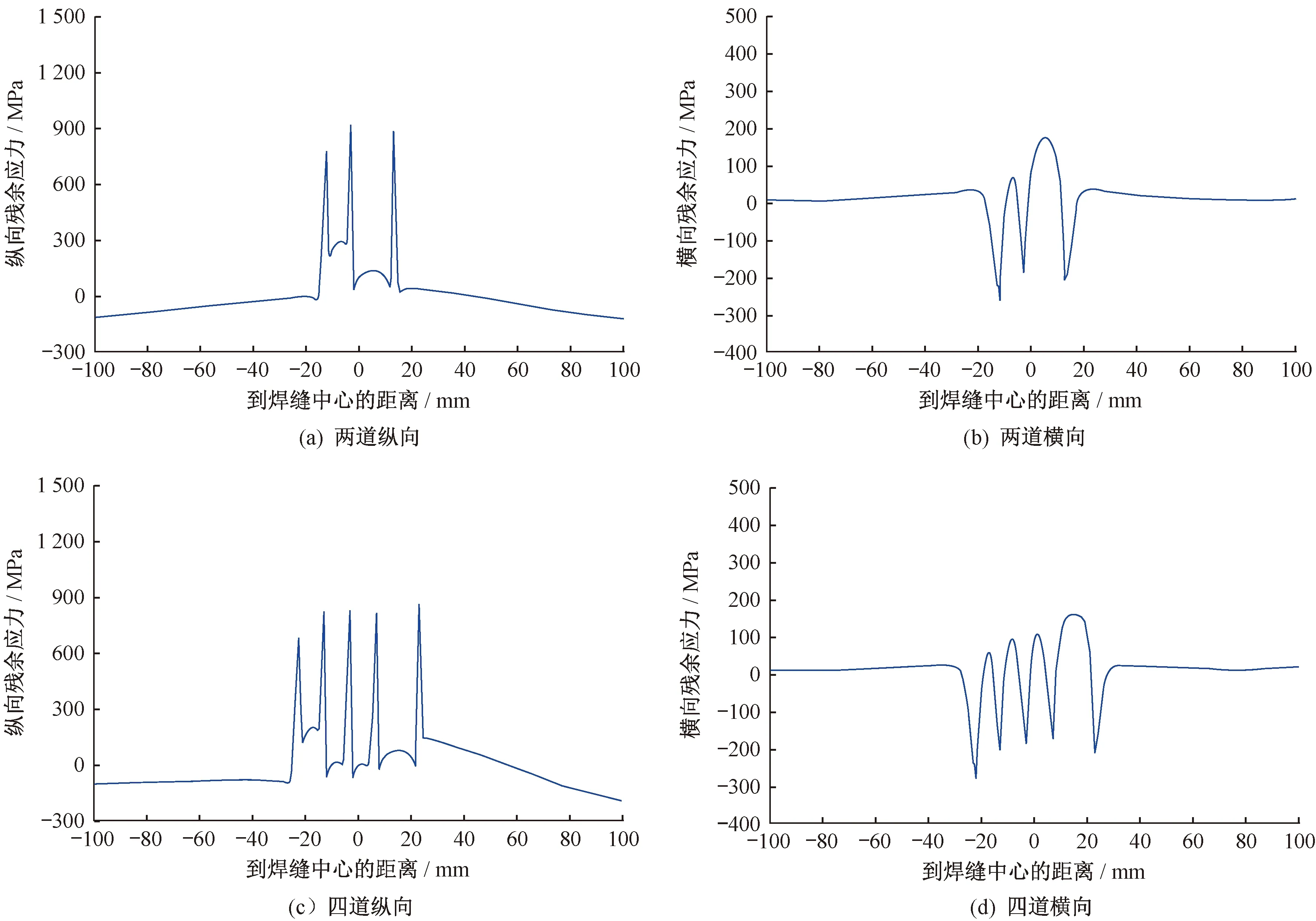
图12 中央截面上表面残余应力分布

5 结论

(1) Q960超高强钢单道重熔焊接接头温度场、残余应力分布的数值模拟与试验结果基本吻合,说明本文中的数值模拟方法具有较高的准确性。

(2) 考虑固态相变的影响,能够显著降低焊缝中纵向拉伸残余应力的大小,但不能改变残余应力数值的符号;对横向残余应力而言,不但能改变横截面上的分布,还使得应力峰值大小发生变化。

(3) 纵向残余应力在热影响区出现局部应力峰值,而焊缝中心纵向应力值显著下降;焊缝中心的横向残余应力呈“阶梯”趋势上升,且在热影响区位置出现局部压应力峰值。

致谢感谢重庆大学邓德安教授对本文研究工作的指导以及对数值模拟算例的帮助。