涉水振动、噪声控制橡胶（上）

侯永振

涉水振动、噪声控制橡胶（上）

侯永振

主要论述涉水振动和噪声控制橡胶涉及的有关原理及相关技术，包括衰减共振、隔离高频振动、附加阻尼处理、噪声控制（相对于减、隔振和附加阻尼处理）与水中应用橡胶的关系和相关影响。

减振；隔振；阻尼；噪声；橡胶；动态力学性能；水声

1 概述

通过衰减或隔离振动，从而对振动与噪声进行控制的方法有减振、隔振和附加阻尼处理，附加阻尼处理又包括自由型阻尼处理和约束型阻尼处理等。

减振是侧重衰减共振振幅，隔振则是指隔离高频振动，附加阻尼处理是借助材料的附加阻尼来衰减弯曲振动，最终都是要达到控制振动与噪声的目的。无论是减振、隔振，还是附加阻尼处理都是利用了橡胶的一些综合性能外加某种特殊性能，如动态力学性能。因此，动态力学性能是联系橡胶与减、隔振及附加阻尼处理之间的桥梁。

橡胶应用于水声学方面的吸声处理，是通过橡胶材料将辐射的声波尽可能多地吸收掉，达到降低回波信号的目的。

2 涉水振动控制中的减、隔振与橡胶

从振动力学角度，橡胶减、隔振器可等效视为振动系统的减振或隔振支撑来进行研究。

一维机械振动的振动力学模型（积极隔振）如图1所示。

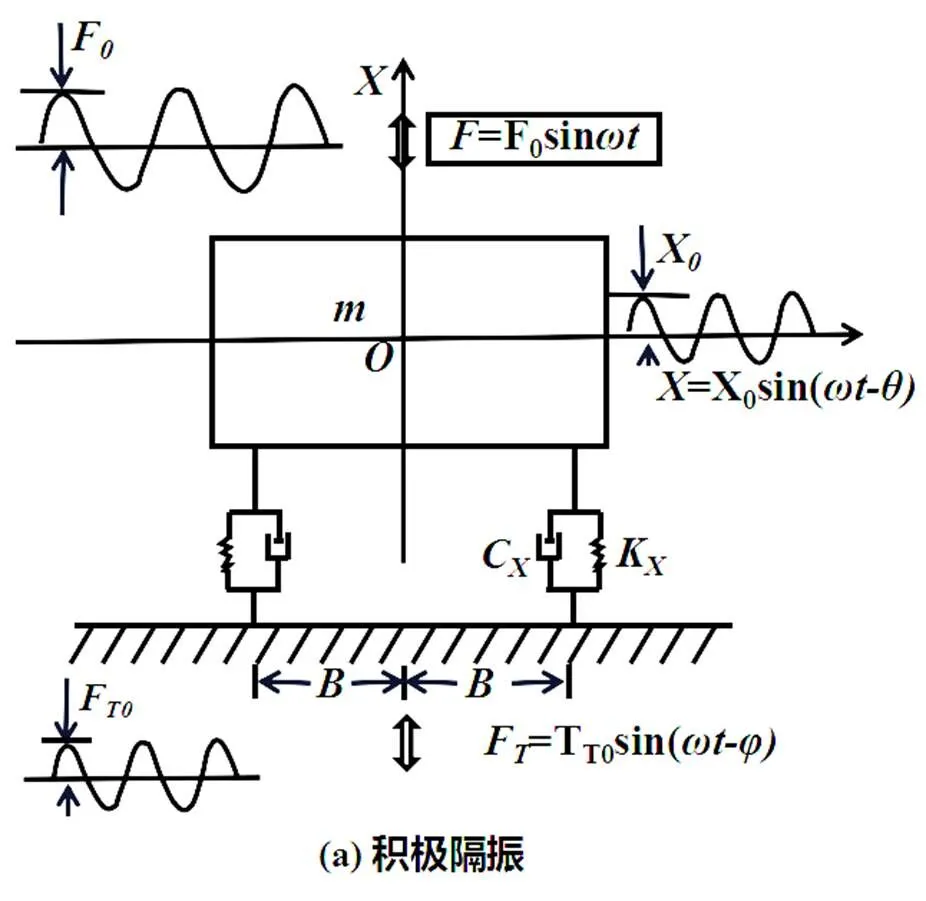
图1 单自由度机械振动的力学模型

这是一个有阻尼的强迫振动，阻尼来源于橡胶材料（包括阻尼橡胶材料）。仅考虑垂直方向的一个自由度的运动情况。

在图1中作用在物体上一共有四种力(假设力向上为正)：

1）扰动力（激励力）：F0·sinωt

2）物体重力(荷载)：-W

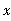
图中：F0为扰动力（激励力）的幅值，FT0为传递力的幅值，X0为物体振动的幅值。

根据牛顿定理，对图1所示的系统可列出如下的物体运动微分方程式：

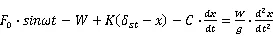
经过整理可化简为:

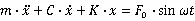
这就是强迫振动的运动方程式。就小阻尼的隔振系统来说，方程式（2）的全解为:

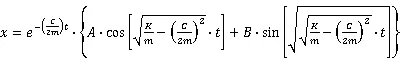
公式（3）的曲线表示为图2。

上式中第三项为特解，是有阻尼的强迫振动，一般实际问题中只注意强迫振动部分：

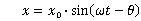
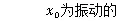
θ为振动的相位角。

则：

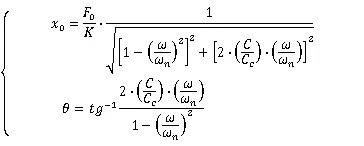
式（7）表明振动物体的响应是频率的函数，在各种频率范围内的响应特性，如表1所示。

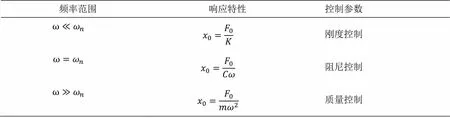
表1 各种频率范圈内的响应特性

此表指出了每一种系统参数——质量、刚度和阻尼，只能在有限的频带范围内有效地控制响应，如阻尼只在共振区显出其功效。

经过处理，得出如下的经典振动传递率表达式

由（9）式决定，绝对传递率是系统频率比Z和阻尼比的函数。函数表达式作出的曲线图如图3所示。

减振或隔振橡胶应用，就是需要研究橡胶材料阻尼等随这个阻尼比和频率比变化的曲线族，涉水橡胶则要研究橡胶在附加水中应用条件下的材料阻尼等性能随阻尼比和频率比变化的曲线族，吸水、透水、水解、以及由水的静压力作用等直接或间接引起的物理变化，包括通过刚度或材料弹性模量引起的应力应变变化和化学变化，都会对最终的衰减共振或隔离高频振动产生影响。

由图3可以看出：

根据固有频率公式：

在设计橡胶或橡胶金属减振器或隔振器时，很重要的一点就是，需要考虑橡胶材料弹性模量在附加水的影响条件下，随温度变化的K值的影响。比如，聚氨酯橡胶可能就会因为其附加水的条件影响，弹性模量随温度变化，通过对材料与制品刚度K值的影响，造成曲线随温度变化漂移。

在稳态振动中，橡胶材料经历一个正弦交变应力振动周期损耗的能量，或由于分子链段内摩擦运动将振动能或声能转化为热能耗散在周围环境的能量，关系式如下：

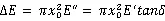
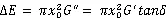
式（11）是拉伸模式的表达式，式（12）是剪切模式的表达式。

（11）和（12）式表明在每一循环周期中，单位体积试样损耗的能量正比于损耗弹性模量和应变振幅的平方；或正比于贮能弹性模量、应变振幅的平方及损耗因子。

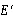
高耐磨炭黑含量：1.30%；2.20%；3.15%；4.10%；5.5%

图4 填充高耐磨炭黑的丁基橡胶胶料的δ随应变振幅的变化的曲线

不论是用作衰减共振，还是用于隔离高频振动，拟或既考虑衰减共振又考虑隔离高频振动，因为必须考虑橡胶承力，及其所涉及的疲劳老化和失稳问题，所以，这类应用主要是利用橡胶在高弹态（橡胶态）的动态力学性能，包括阻尼性能，处于高弹态的橡胶的阻尼要显著低于处于玻璃化转变区的橡胶自身的阻尼。

几种橡胶处于高弹态的损耗因子（用于表征橡胶处于高弹态的阻尼）见表2。

表2 几种橡胶处于高弹态的损耗因子

在一定程度上或从某一角度看，可以通过橡胶的回弹性来间接地粗略判断材料的相对阻尼，回弹性高则橡胶的阻尼低。橡胶回弹性（冲击弹性）随温度变化的典型曲线见图5。

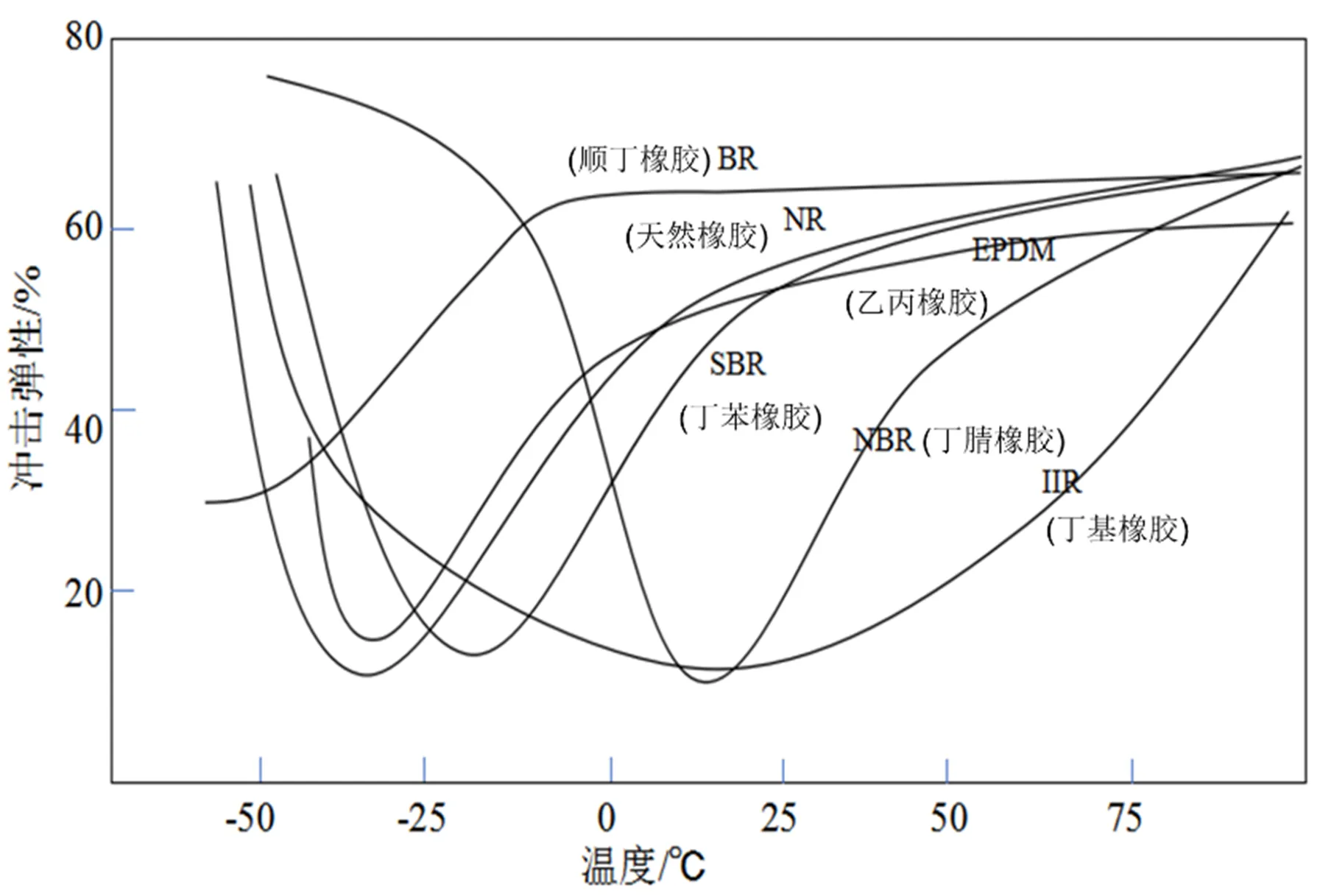
图5 橡胶冲击弹性随温度变化的典型曲线

恒定频率下，橡胶材料随温度升高依次进入玻璃态区、玻璃化转变区、橡胶态（高弹态）区以及粘流态区而呈现出的动态力学性能变化图见图6。

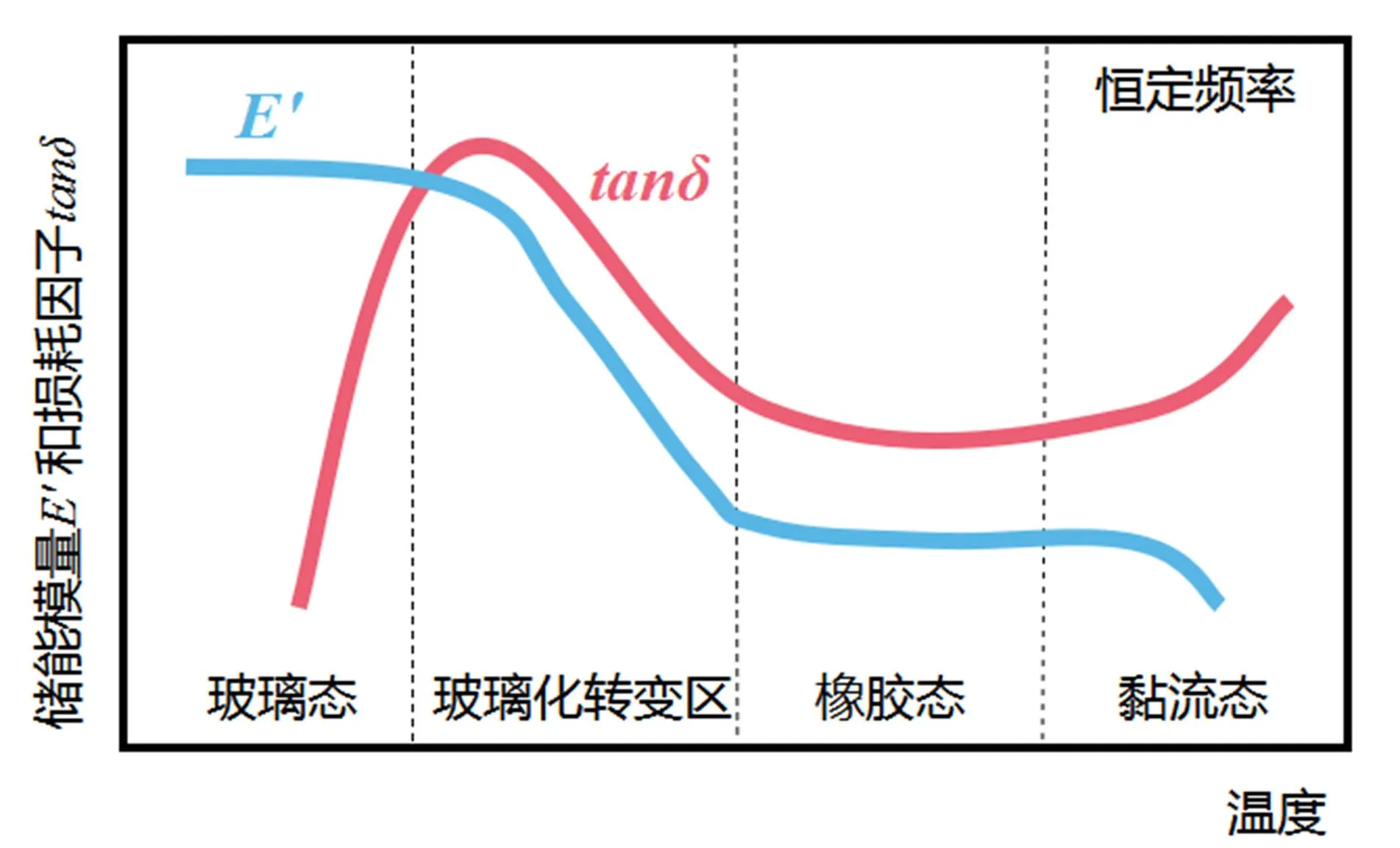
图6 橡胶材料随温度升高依次进入玻璃态区、玻璃化转变区、橡胶态（高弹态）区以及粘流态区而呈现出的动态力学性能变化

常用橡胶材料随温度升高依次进入玻璃态区、玻璃化转变区、橡胶态（高弹态）三区而呈现出损耗性能（表征参数为tanδ）变化的曲线见图7（Tg为玻璃化转变温度）。

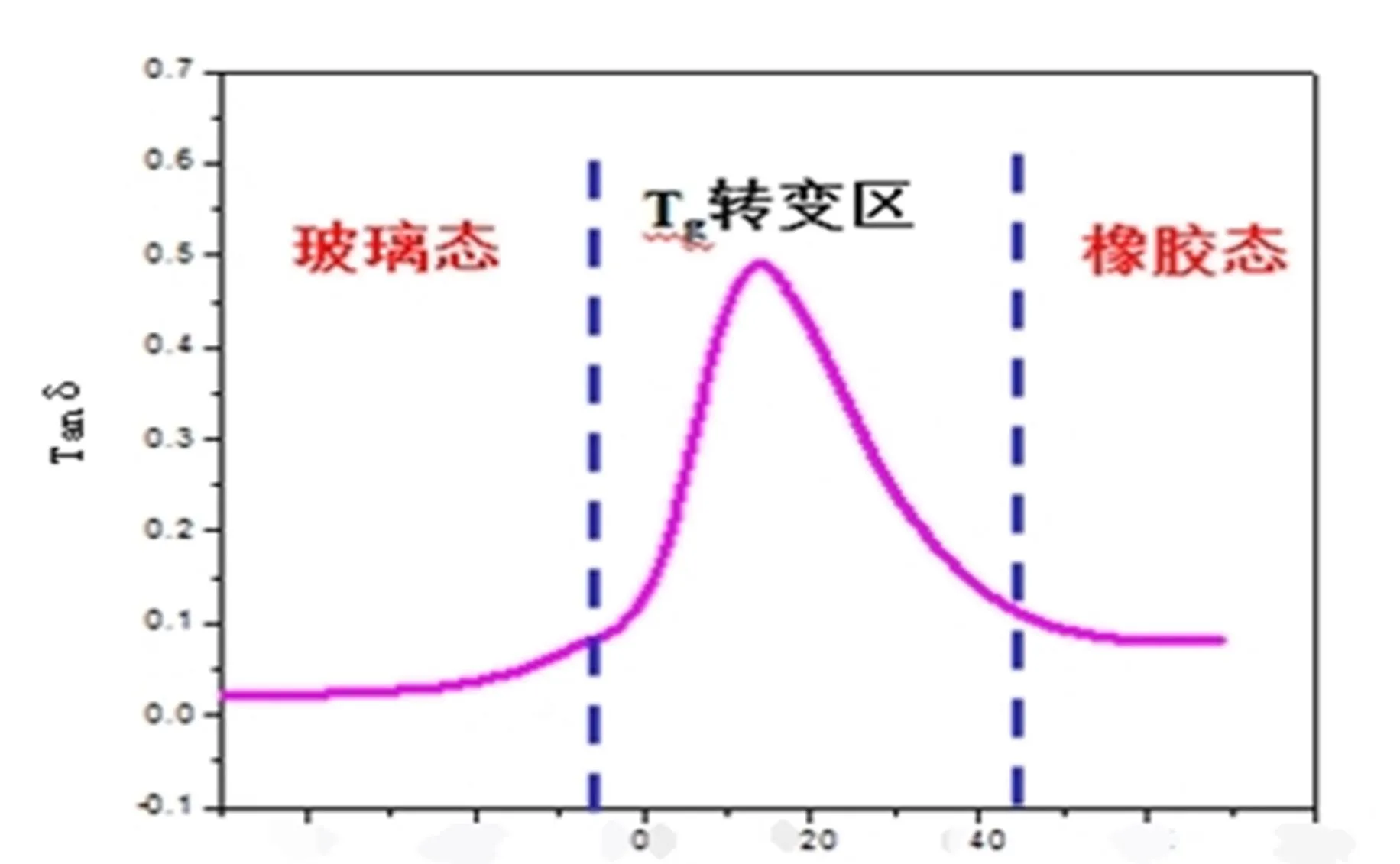
温度/℃

常用橡胶材料在恒定温度下随频率升高依次进入橡胶态（高弹态）、玻璃化转变区、玻璃态区三区而呈现出的动态力学性能（E′、E″、tanδ）变化曲线见图8。

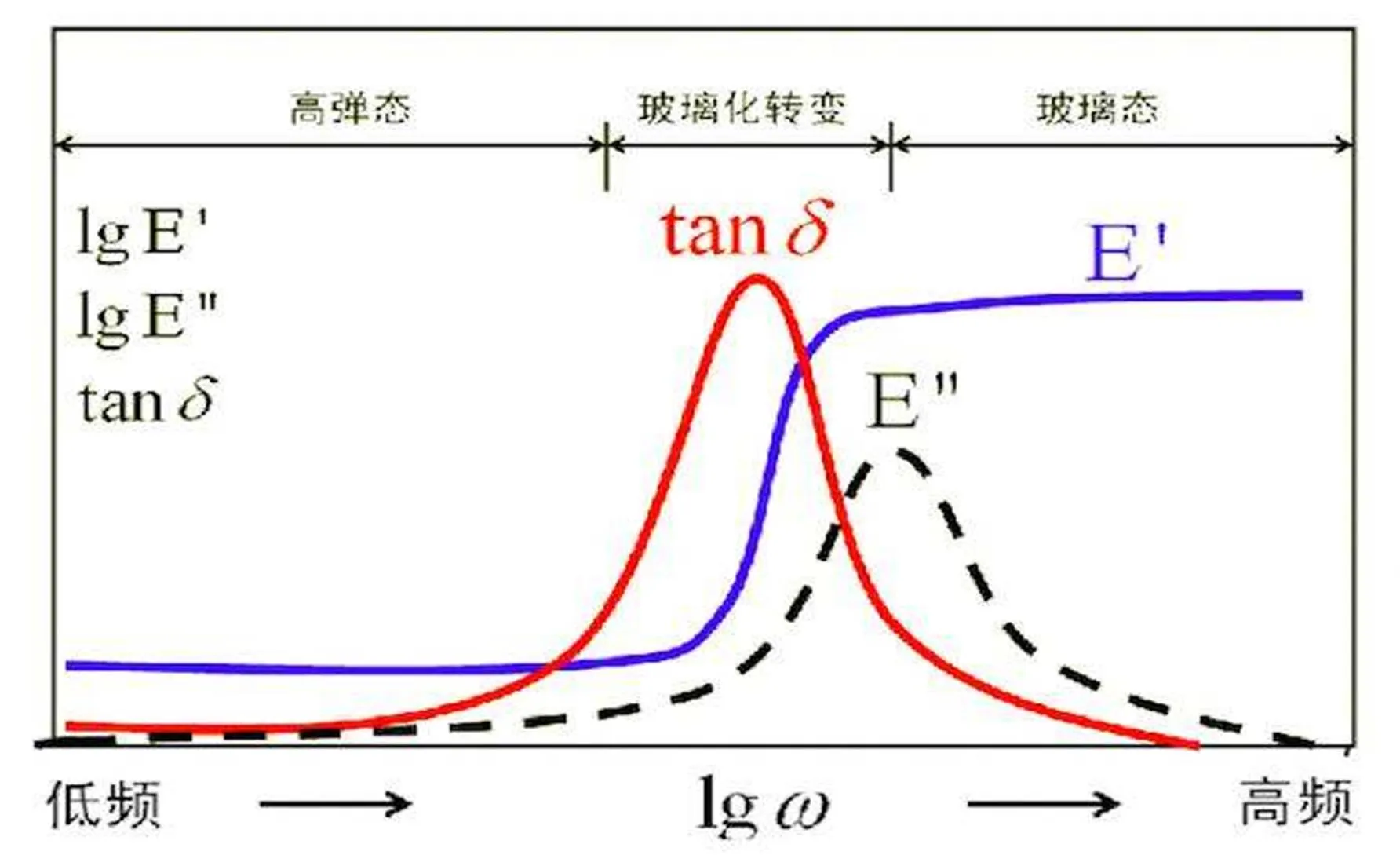
图8 常用橡胶材料在恒定温度下随频率升高依次进入橡胶态（高弹态）、玻璃化转变区、玻璃态区三区而呈现出的动态力学性能（E′、E″、tanδ）变化曲线

典型的动态力学性能三维曲面图见图9。

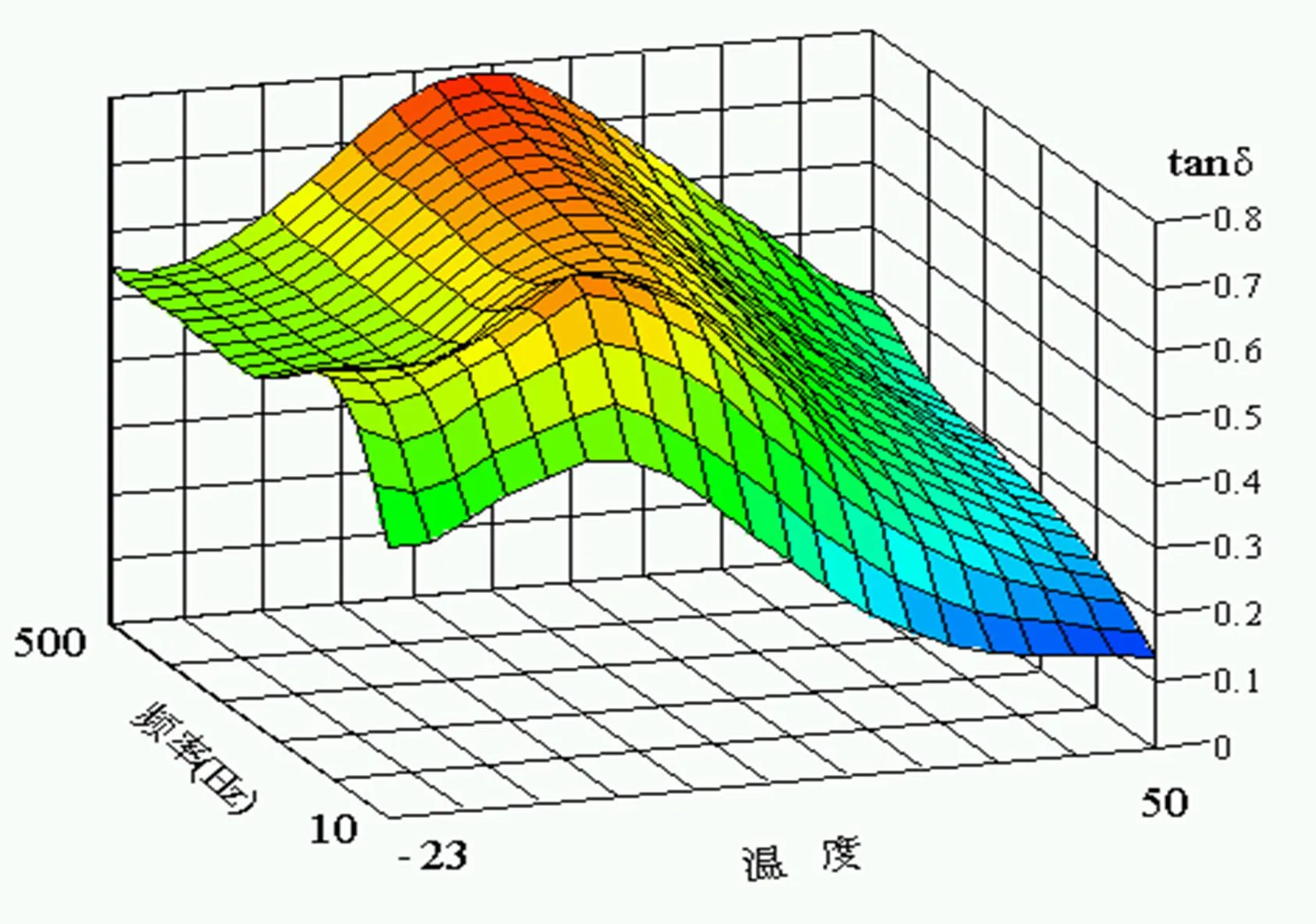
图9 典型动态力学性能三维曲面图

某种橡胶材料用作减、隔振时，由于温度变化而对传递率（TA）曲线随频率变化造成的漂移影响见图10。

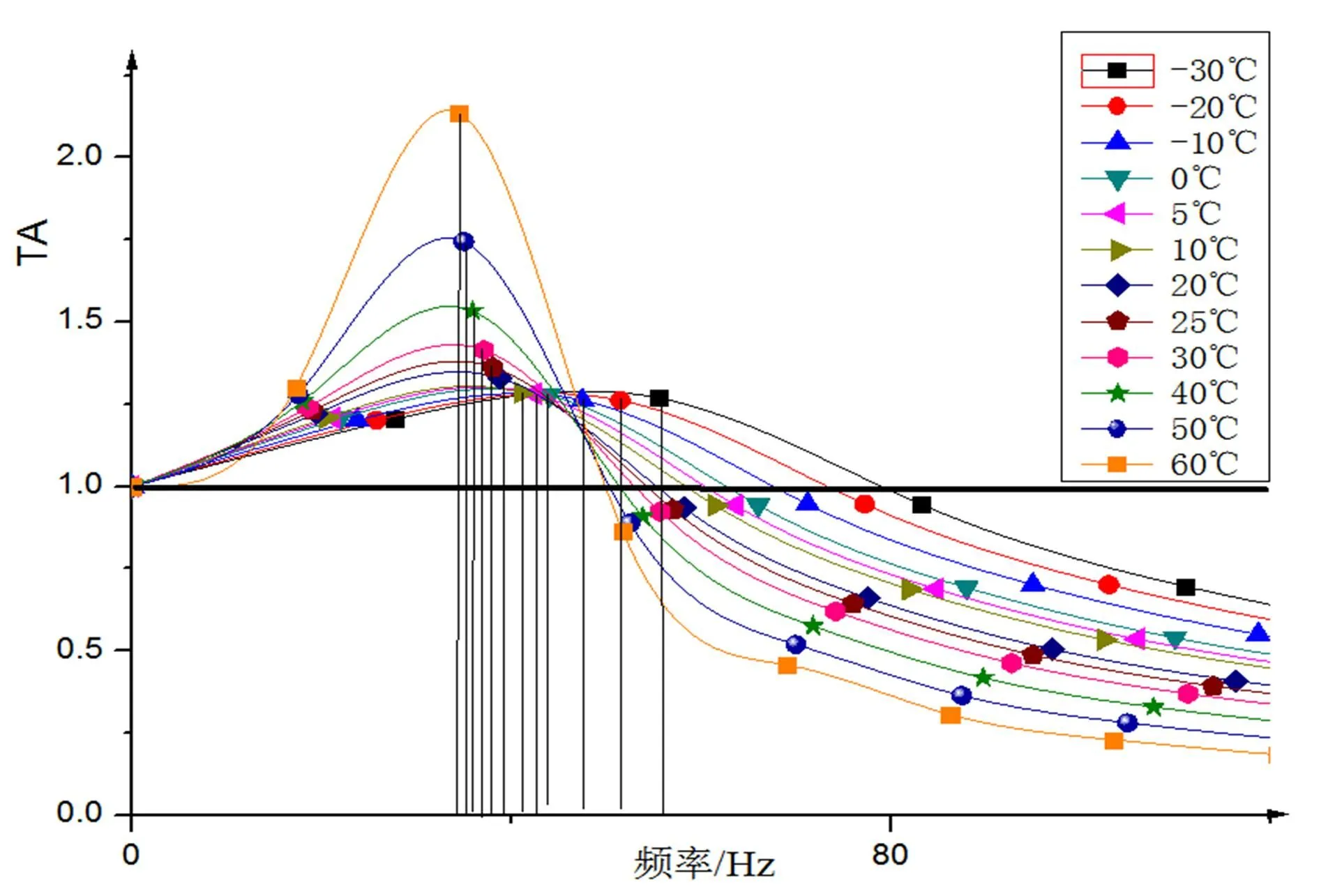
图10 胶料动态力学性能随温度变化对减振和隔振性能随频率变化造成的漂移影响曲线

减、隔振器的性能优劣与是否实用，取决于附加水中应用条件下的结构设计、橡胶材料阻尼和刚度随温度、频率及应变振幅变化和物理化学变化比如疲劳老化综合优化的结果。这其中有些工作可以通过振动模态分析与有限元模拟等来进行预估。

从其复杂性和对问题分解的角度看，有必要把减、隔振器的结构设计、振动模态分析和有限元模拟作为一个研究维度来进行研究；把橡胶的分子模拟、材料选择与配方设计，加工工艺、性能研究，尤其是动态力学性能研究作为一个维度来进行研究；以及把涉水应用的减、隔振性能以及声学性能研究作为另外一个维度来进行研究。

(未完待续)

侯永振，正高级工程师，主要从事阻尼与声学橡胶材料及制品、橡胶防腐蚀衬里、胶黏剂与密封腻子等研究。