课堂教学中对一题多解的点滴感悟

刘培聚 孙海燕 郭 丹

(黑龙江省安达市任民镇中学校 151423)

孙海燕(1976.11-),中学一级教师,从事初中数学教学研究.

郭丹(1994.9-),中学二级教师,从事初中数学教学研究.

近期，在讲授相似三角形的判定与性质的习题课中有如下的精彩片段：

片段一：如图1，在△ABC中，AB=AC,以AC为直径的⊙O交AB于点D，交BC于点E.

(1)求证：BE=CE；

(2)若BD=2，BE=3，求AC的长.

问题(1)比较简单，连接AE，利用直径所对的圆周角是直角，结合等腰三角形的三线合一解决问题，或者连接OE，利用三角形中等边对等角证明OE∥AB，从而使问题得到解决.

问题(2)，我预设的是利用相似三角形的判定与性质解决问题.但康同学的解法是：如图2，连接CD，利用勾股定理求出CD2=32，再在Rt△ADC中设AB=AC=x,则AD=x-2，由勾股定理列方程得x2=(x-2)2+32，解方程求出AC的长.

康同学能在两个直角三角形中各用一次勾股定理解决求边长的问题，说明他已经能够灵活运用勾股定理来解题了.对于康同学的解法，我给予了肯定与赞同.同时，我又启发学生思考还有没有其它解法？通过给予学生足够的交流探究的时间，学生们找到了利用相似三角形的知识解决问题的方法，思路如下：

如图3，连接DE, 利用圆的内接四边形内对角互补，可证得∠BDE=∠C,又由∠B为公共角可证得△BDE∽△BCA,根据对应边成比例，求出线段AB的长，即得到AC的长.

由此可见，在课堂教学过程中，不断给予学生鼓励和赞许，使得他们能够有信心多思考，有勇气表达自己的想法.这样，教师才能根据课堂反馈的信息，针对学生的掌握情况，制定有效的教学计划,从而达到事半功倍的效果.

片段二：已知：如图4,在△ABC中，∠BAD=∠C,∠DAE=∠EAC.

由于正在学习相似三角形，因此我的预设是学生可以利用相似和平行线分线段成比例定理解决问题.但阮同学经过思考后认为三角形的形状固定，面积唯一，可以利用面积法解题.证法如下：

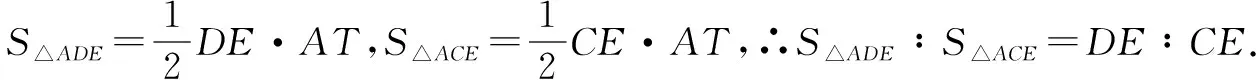
经过思考后，郝同学认为，利用平行线构造相似三角形，同时可以得到等腰三角形，转移线段，从而解决问题.思路如下：

在上述过程中，学生经过启发，能够在已有知识的基础上尝试利用一题多解的思路去解决问题，这与平时注重训练学生先独立审题， 再小组合作，深入探究是分不开的.训练时老师一定要沉住气，不能急于一时，你若代替学生说，他们以后就不会努力认真思考，更不会另辟蹊径，长此以往，学生自主解决问题的能力也随之下降.所以对学生的思维训练不能急于求成，课堂点拨之后，要给足学生思考的时间，要坚持培养学生独立解题能力.

片段三：如图7，矩形EFGO的两边在坐标轴上，点O为平面直角坐标系的原点，以y轴上的某一点为位似中心，作位似图形ABCD，且点B,F的坐标分别为(-4,4)，(2,1)则位似中心的坐标为____.

隋同学的想法是用待定系数法求出直线BF对应的函数解析式，进而求出与y轴的交点坐标.解法如下：

此题的解法也不局限于运用函数思想.于是我又启发学生思考能否利用求线段长的方法求位似中心的坐标呢？学生独立思考后，邱同学给出了如下解法：

设直线BF交y轴于点H，证明△BCH∽△FGH，由点B(-4，4)和F(2，1)可得BC=4,FG=2,CG=3.由相似的性质可得CH∶GH=BC∶FG=2∶1.∴HG=1，∴OH=2.即位似中心的坐标为(0，2).

在课堂教学中给学生时间探究，鼓励学生多方位的思考问题，寻找不同的解题思路，并且总结所用的方法，找出其联系和区别，看似多用了一些时间，但是对学生的思维训练是水滴石穿的磨砺，且贵在坚持，让学生从“学会”到“会学”.

我所展示的几个片段在我们的日常教学中，一定都常见，那就让我们把它们好好留存，并对其进行编辑整合，去其糟粕，留其精华,使它如钻石般璀璨.通过一题多解，开阔学生的视野，挖掘学生数学思维的深度，把培养学生的学习技能和方法指导实施在有效的课堂中，学生的创新探究精神会因为教师的放手去做，达到新的高度.

总之，通过不断的积累，使得学法和教法都能够有所提升，虽然这是一个很漫长的培养过程，但是一定要坚持去做.多给学生时间，也是给自己的教法更大的空间.点滴感悟与反思，旨在更好的成长，我知道教法之路漫漫其修远兮，吾将上下而求索.