考虑级配空间随机特性的堆石坝变形应力分析

朱 晟，卢知是

(1.河海大学水文水资源与水利水电工程科学国家重点实验室，江苏 南京 210098；2.河海大学水工结构研究所，江苏 南京 210098 )

近年来，西部地区一批300 m级高心墙堆石坝即将开工建设，高堆石坝的变形控制问题成为设计研究的重点。已有研究表明，堆石料的级配分布显著影响其物理性质和力学行为，且随荷载增大，相关性明显提高。陈镠芬等[1]通过三轴剪切试验发现堆石料级配的分形维数越大，各围压下峰值强度越大；赵婷婷等[2]基于颗粒流方法进行数值试验，认为分形维数可用于量化分析堆石料力学特性；加力别克等[3]通过三轴压缩试验，得出分形维数与其抗剪强度、破坏比、切线模量等邓肯E-B模型参数之间存在二次函数关系；朱晟等[4]分析了级配与抗剪强度、剪胀性、压缩性及颗粒破碎之间的规律，建立了广义塑性模型参数与分形维数之间的函数关系。

目前高坝的变形与应力研究成果，绝大部分以各分区坝料采用单一级配的假定为基础。然而堆石料级配存在分布上的空间变异性，且受自然条件、岩石性状、填筑过程等因素影响，表现出结构上的不确定性，按单一级配计算不能完全反映工程实际。Vanmarcke[5]用齐次正态随机场模拟土性剖面，建立了岩土参数随机场模型。我国专家学者如张征等[6]将地质学方法应用于岩土参数分析，拓展了随机场理论及应用；蒋水华等[7]提出了考虑空间变异性的非均质边坡可靠度分析方法；刘鑫等[8]采用随机极限平衡法发现边坡破坏的演化与土体参数的空间分布密切相关；杨鸽等[9]在对筑坝料随机场进行地震响应分析时，得出忽略材料不确定性的方法会较大程度低估坝坡危险性。

已有的随机有限元研究主要针对边坡稳定问题，而对于级配参数空间随机分布的研究成果较为稀缺。为此，本文引入地质统计学方法，结合施工填筑检测资料，模拟级配参数的空间随机分布，进行考虑级配效应的变形与应力研究，为高心墙堆石坝的变形控制问题提供新的思路。

1 坝壳料级配分形分布模型

已有研究成果[10-13]表明，粗粒土在不同的粒度范围内均表现出良好的分形性状，分形维数D已成为表征岩土材料物理力学性质的重要指标。对于堆石料，采用颗粒质量的分形分布模型，即

(1)

式中：P(di)——小于di的颗粒质量占比；di——颗粒直径；dmax——最大粒径。

结合建设中的两河口心墙堆石坝检测级配，采用分形分布拟合坝料的颗粒级配曲线如图1所示，相关系数均大于0.989，基本满足分形分布。

图1 两河口心墙堆石坝填筑级配曲线Fig.1 Grading curve of Lianghekou rockfill dam

对堆石料、过渡料检测级配的分形维数值分别进行K-S正态分布检验，双侧相伴概率值p分别为0.395、0.194，均大于0.05，因而各分区分形维数D满足正态分布。由于心墙、垫层、反滤料分形维数的变异系数均小于1%，级配差异相对较小，故本文着重研究堆石料、过渡料等粗粒料的空间随机分布，假定其他分区填料为单一级配，计算时参数作均一化处理。

表1 分形维数D统计特性

分形分布模型能够定性、定量描述已知级配检测点的信息，然而难以掌握空间其他位置点的信息，大坝整体结构仍存在很大的未确知性，需进一步研究分形维数D在坝体内的空间分布。

2 级配空间变异结构分析

地质学中，以空间坐标x1、x2、x3为自变量的随机函数Z(x1,x2,x3)=Z(x)称为区域化变量[6]，其方差为

Var[Z(x)-Z(x+h)]=E[Z(x)-Z(x+h)]2=2γ(h)

(2)

式中：h——检测点间距；E——期望值；γ(h)——变异函数，用来描述空间点之间的差异性和相关性。

散布于坝体内、与空间位置相关的级配参数即可看作区域化变量。选取两河口心墙堆石坝距左岸坝肩335.94 ～ 347.79 m(最大断面坝段)的检测级配共54组，空间位置如图2所示。由于两河口工程尚处于在建阶段，故本文研究只应用1/3坝高以下的检测级配资料，通过计算较低高程处分布的坝料测点的空间相关性，近似模拟整个断面级配的空间分布。

图2 大坝填筑检测级配分布(单位：m)Fig.2 Detecting point distribution of dam material gradation (unit: m)

为保证随机模拟精度，需试算合理的变异函数理论模型。利用GS+、Arcgis等地质统计学软件计算变异函数，根据样本值计算γ(h)的估计量γ*(h)，用理论变异函数模型对γ*(h)做回归拟合，并选定误差最小模型作为理论模型。计算时需设置最大步长和Lag步长等参数，最大步长为分离距离的最大值hmax，通常为L/2(L为区域内沿某方向的最大尺度)[14]。该堆石坝散布的检测点间距最大值为894 m，故选择447 m作为最大步长值。由于计算数据量要求对应每个样本间距值的点对至少为30对，经试算选定合理步长值为65.6 m。以堆石料为例，变异函数理论模型及模型参数模拟结果见表2。

表2 变异函数理论模型及参数模拟结果

区域化变量的相关程度有对应的分级标准[14]，当块金系数C0/(C0+C)≤25%、=25%～75%、>75%时，分别对应强烈、中等、微弱的3种空间相关程度等级。根据表2，球状、指数、高斯模型的块金系数分别为16.15%、8.69%和18.88%，表明分形维数具有强烈的空间自相关性。其中，指数模型离差平方和更小、R2更大、块金系数更小，故选定指数模型作为堆石料分形维数D的变异函数理论模型，如图3所示，横轴为步长值限定下的所有点对距离的平均值，纵轴为对应于离散点的变异函数值。

图3 变异函数指数模型拟合曲线Fig.3 Fitting curve of exponential model for variogram

计算得到堆石料级配参数的变异函数指数模型拟合公式为

γ(h)=0.000 229+0.000 118 9(1-e-h/63.9)

(3)

重复上述步骤对过渡料进行变异函数计算，选择高斯模型为变异函数理论模型，公式为

γ(h)=0.001 13+0.011 69[1-e-(h/236.4)2]

(4)

将空间距离h作为主要参数，借助变异函数理论模型明确了空间各位置点参数间的相关性和依赖性，在此基础上对分形维数D的空间分布进行随机模拟。

3 级配空间随机分布模拟

3.1 随机有限元离散方法

采用中心点法对坝壳料级配参数的空间分布作离散化处理。将最大断面坝段视为空间几何域V，并划分为n个子单元V1、V2、…、Vn，用Z(x)在Vi(i=1,2,…,n)中点xi的值Z(xi)来表征单元体Vi的特征，即可离散得n个随机变量Z(x1)、Z(x2)、…、Z(xn)。为便于计算分析，依据坝体有限元剖分网格对分形维数D进行空间离散，采用空间8节点等参单元，共811个单元、1 625个节点，如图4所示，沿垂直于坝轴线从上游到下游为x轴正向，沿坝体高程方向为y轴正向。

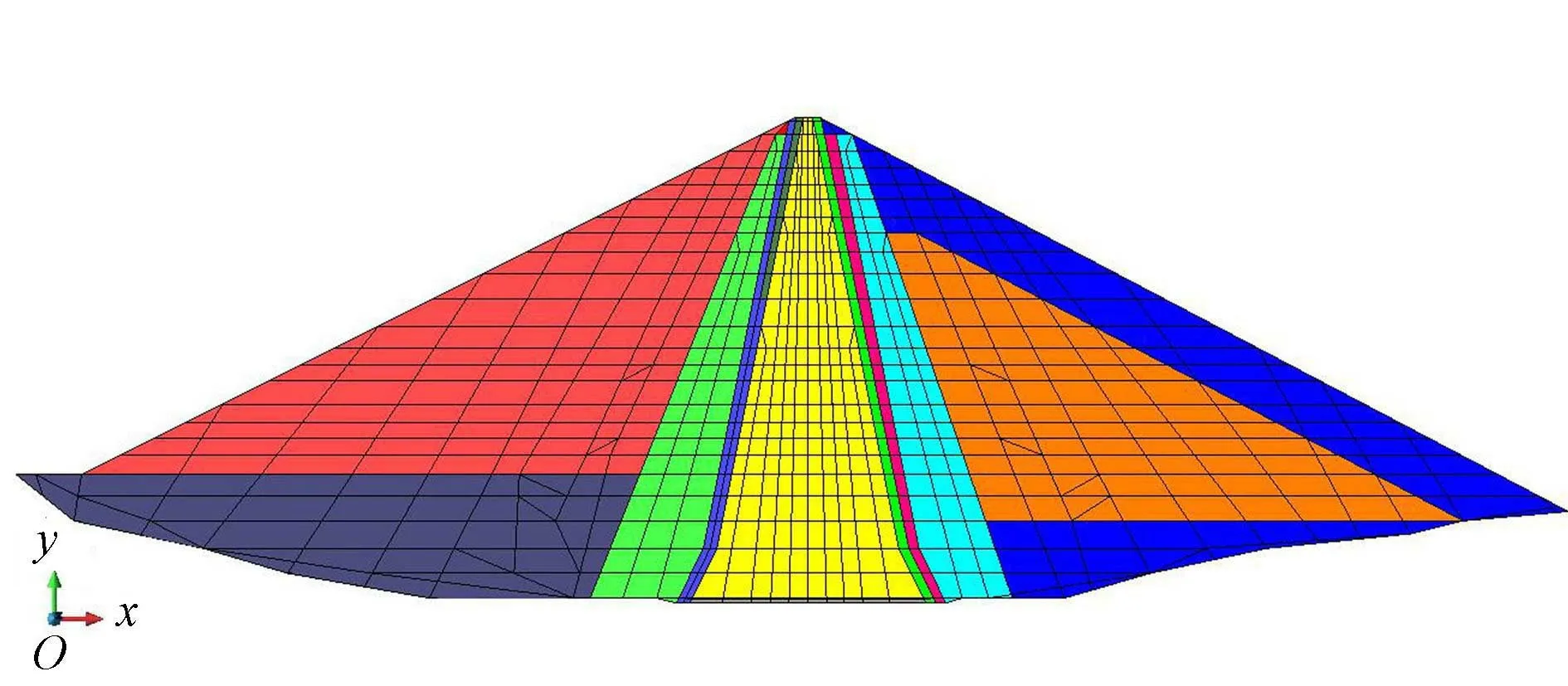
图4 大坝有限元网格剖分示意图Fig.4 Finite element meshing of the dam

3.2 克里金估计方法

克里金估计方法通过对已有数据加权线性组合，采用拉格朗日乘数法求解可得分形维数D在无偏性条件和估计方差最小原则下的线性估计量[15-16]，是较优秀的线性无偏估计方法。估计采用克里金估计方法对坝体内未检测的级配不确知点进行随机估计，将估得的Z*(xi)值赋给Vi对应的随机变量Z(xi)。

由于克里金估计方法对正态分布的数据预测精度最高，且分形维数D服从正态分布，因此精度能够得到保证[17]。对堆石料、过渡料级配空间离散单元进行随机内插，将某次估计结果绘制成空间随机分布图如图5所示，受空间不同位置点的相关性影响，级配参数表现出局部随机性和整体结构性，这是空间变异性的主要特征。由于级配测点集中于坝体较低高程，较高高程处的离散点间距h较大，空间依赖性降低，一定程度上影响了较高高程处的模拟精度。

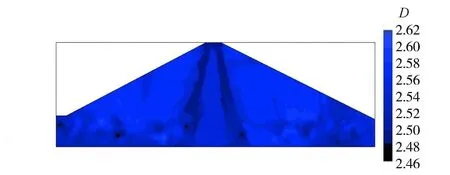
图5 坝料级配参数的空间随机分布Fig.5 Spacial random distribution of gradation parameter of dam material

3.3 随机模拟精度验证

用交叉证实法验证空间随机模拟的精度，其原理为：将各已知点Z(x)暂时从数据系列中除去，根据其他已知点测值、克里金估计方法和变异函数理论模型计算该位置处的估计值Z*(x)，并将Z*(x)放回数据系列，对各点依次遍历可得Z*(x1)、Z*(x2)、…、Z*(xn)的新数据系列，并将其与原始数据系列Z(x1)、Z(x2)、…、Z(xn)进行统计比较。对图5模拟结果进行交叉验证，结果如表3所示，堆石料、过渡料的标准差分别为0.085和0.076，数值较小，相关系数分别为0.785和0.712，认为变异参数模型合理，插值精度较高。

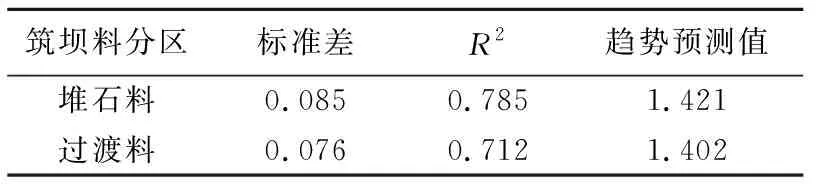
表3 交叉验证精度评价

4 心墙堆石坝随机有限元静力分析

4.1 静力计算

考虑到单次模拟的随机性，应重复以上方法对分形维数D的空间分布进行多次随机模拟，并将模拟结果应用于有限元计算，直至主要计算值统计结果趋于稳定。材料的本构模型选取广义塑性模型。朱晟等[4,18]以国内外典型高坝的试验资料为依据，建立了广义塑性模型参数与分形维数之间的函数关系式，可用于考虑填筑级配影响的土工计算。

基于文献[4,18]中一一对应关系，可得考虑随机特性的广义塑性模型参数，并针对各次模拟进行静力计算分析。借鉴Griffiths等[17]对于随机模拟稳定的判定方法，绘制主要计算结果的滑动平均值(running average)随模拟次数n的波动曲线，设第i次模拟得到的计算结果为ri，则滑动平均值定义为

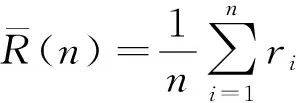
(5)

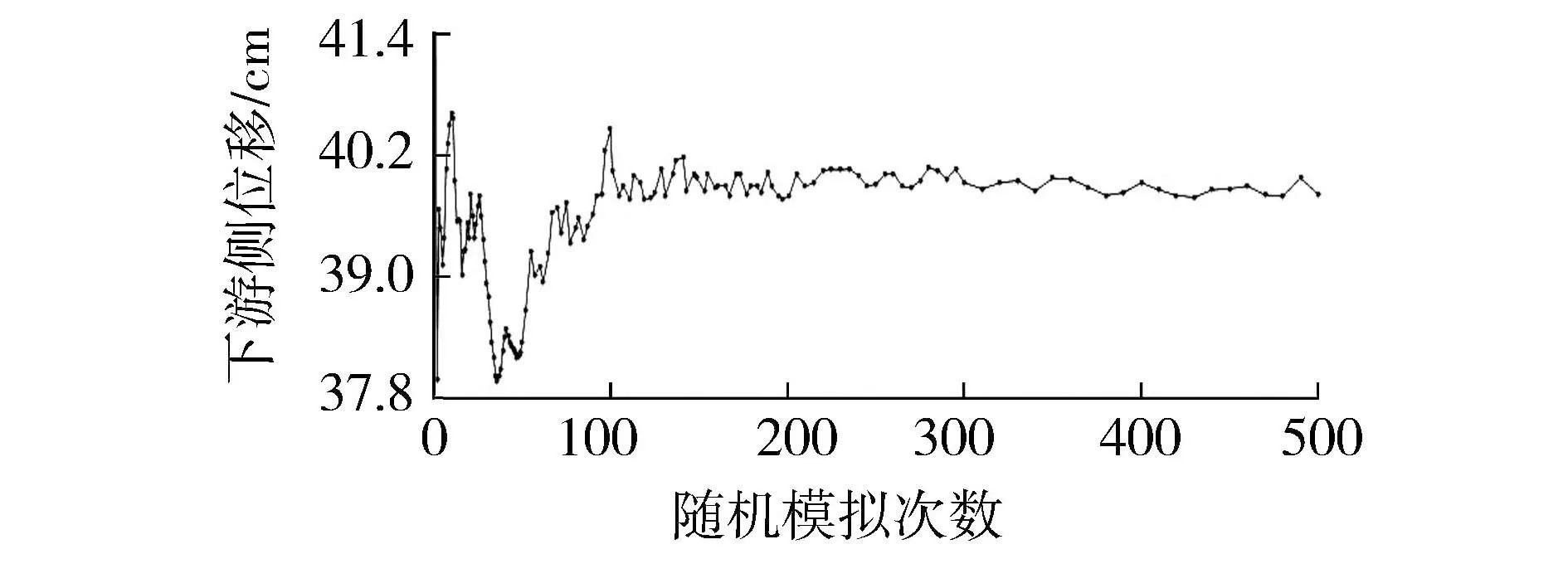
图6 下游侧位移的滑动平均值随模拟次数的波动示意图Fig.6 Fluctuation diagram of moving average with simulation number for displacement in downstream

表4 材料随机参数统计特性

4.2 计算结果统计分析

4.2.1 变形和应力

图7为第50次随机模拟得到的位移和应力分布。对500组考虑随机特性的静力计算结果做K-S正态分布检验，得下游侧位移、上游侧位移、最大沉降量、第一主应力、第三主应力假设检验的显著性概率分别为0.932、0.474、0.864、0.580和0.973，均高于0.05，满足正态分布。

图7 第50组随机有限元方法计算结果Fig.7 Results of 50th group of stochastic finite element calculation

确定性有限元方法的计算结果与随机模拟结果的统计均值对比如表5所示，随机方法计算得到最大沉降量均值、下游侧位移和上游侧位移分别为363.95 cm、40.119 cm和39.072 cm，均大于确定性有限元计算结果，相对误差为10%左右。由于考虑随机性得到的各组计算值均服从正态分布，且正态分布具有对称特性，即p(xi，μ)=50%，若忽略堆石坝结构的不确定性，仅按单一参数进行有限元计算，则有超过50%的可能性会低估坝体变形和应力，不利于探究更为安全经济的高堆石坝设计方案。因而认为考虑随机特性进行稳定分析和结构设计时，结果偏于安全和可靠。

表5 随机性有限元与确定性有限元计算结果对比

4.2.2 心墙的拱效应

由于拱效应的作用将使心墙竖向应力降低，从而导致心墙内产生裂缝或水力劈裂，合理评估心墙拱效应是高坝变形控制中十分重要的问题。采用拱效应系数来表征拱效应强弱程度[19]，定义为

(6)

式中：R——拱效应系数；σy——竖向土压力；γ——土体容重；hs——上覆土层高度。

绘制确定性方法和随机性方法[20-23]的拱效应系数R等值线图如图8所示，可见随机有限元方法计算得到的拱效应系数R与常规有限元方法的等值线分布较为接近，能定性表征实际工程中的拱效应问题，验证了随机模拟方法的合理性；两种方法计算结果均呈现出两侧大、中间小的分布规律，即位于心墙中部的土体拱效应更为显著，相对于两侧更易于产生裂缝或发生水力劈裂；从高程分布上看，位于心墙1/2高程处拱效应系数R值较低，拱效应作用更为显著；拱效应系数R越小，表示拱效应越强。随机性方法计算得到的拱效应系数最小值为0.664 5，较传统方法计算得到的最小值0.688 0偏小，表明应用随机性方法进行设计计算，更有利于坝体结构安全与稳定。

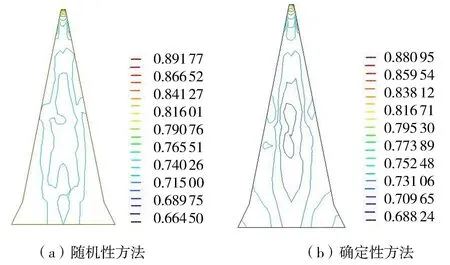
图8 拱效应系数R分布等值线Fig.8 Contour map of arch effect coefficient

5 结 论

a.分形分布可较好地表征级配空间分布，选定指数型、高斯型变异函数理论模型分别描述堆石料、过渡料级配分形维数D的空间变异结构，且块金系数均小于或等于25%，表现出强烈的空间相关性和依赖性。

b.采用中点映射法进行随机场模拟与离散，结果表明，随机模拟达500次时，计算结果趋于稳定。

c.通过工程实例验证，级配分布的随机特性对高堆石坝应力、变形影响明显。相较于材料参数均一的确定性有限元方法，考虑级配参数空间随机特性时，沉降更大，拱效应更明显，有利于探讨更为安全经济的高堆石坝设计方案。