基于Hessian矩阵和支持向量机的CT图像裂纹分割

邹永宁，张智斌，李 琦，余浩松

（1.重庆大学 光电工程学院，重庆400044；2.重庆大学 光电技术及系统教育部重点实验室ICT研究中心，重庆400044）

1 引 言

裂纹分割对工业计算机层析成像（Comput⁃ed Tomography，CT）图像处理具有重要意义，其分割精度和分割准确度直接影响到后期的裂纹测量、分类和显示等。但是，CT图像中的噪声、伪影等干扰会不同程度的对裂纹分割造成影响，因此工业CT图像分割仍是一个具有挑战性的问题。

目前，许多学者提出了各式各样的图像分割方法，且有些方法已应用于CT图像裂纹分割。魏彤［1］等人结合自适应增强算法与分水岭分割算法，实现了图像中的盲道定位。王珏［2］等人使用小波变换增强图像的对比度，然后用RSF模型完成了分割。陈恺［3］等人结合二维熵多阈值分割与萤火虫算法实现了图像的分割。宋巧君［4］等人在双边滤波的基础上结合Black-hat变换和Otsu算法完成了裂缝分割。李玉［5］等人提出了一种利用高斯混合模型的多光谱图像模糊聚类分割方法，实现了高分辨率多光谱图像分割的问题。王雪虎［6］等人提出一种结合先验稀疏字典和空洞填充的方法实现了CT图像肝脏分割。李鹏［7］等人综合考虑图像的灰度像素特征与裂缝的几何纹理特征，提出了结合聚类分析和区域生长算法的路面裂缝分割算法。谢杨灏［8］等人将CT序列图像视为连续变化的视频序列，使用光流网络模型与区域聚类方法完成了分割。王慧倩［9］等人根据CT序列图像的层间相关性与CT图像的最大类熵完成了分割。王艳［10］等人利用遗传算法优化裂缝PCNN模型，实现了裂缝分割。

尽管以上方法都具有较好的分割结果，但均具有一定的局限性，如基于深度学习的方法过度依赖训练样本、结构复杂；基于水平集的方法参数复杂、分割速度慢；基于阈值分割或聚类分析的方法对噪声敏感。支持向量机（Support Vec⁃tor Machine，SVM）在处理小样本、非线性、高维模式识别等问题上有着其独特的优势，而基于Hessian矩阵的多尺度滤波在增强线状结构问题上具有较好的效果，因此本文结合基于Hessian矩阵的多尺度滤波及SVM完成CT图像中的裂纹识别与分割，运用基于Hessian矩阵的多尺度滤波方法获得CT图像中的线状结构，运用SVM分类算法识别图像中裂纹所在的图像块，最后使用自适应阈值分割算法完成裂纹分割，从而提高CT图像中裂纹分割算法的抗干扰性和准确性。

2 原理与方法

2.1 基于Hessian矩阵的多尺度滤波

基于Hessian矩阵的多尺度线状滤波方法当前已有广泛的应用［1，9，11-12］。在二维图像I中，每个像素点I(x，y)处的Hessian矩阵基本形式为：

其 中：Ixx，Iyy，Ixy，Iyx分 别 是 二 维 图 像 在 像 素 点(x，y)处的二阶差分，且有Ixy=Iyx。则QHessian是二维对称正定矩阵，有两个特征值λ1，λ2以及对应的特征向量，其中最大的绝对特征值表示最大的局部灰度变化，其对应的特征向量所指的方向代表了图像变化的方向。

Frangi A F［13］等人结合Hessian矩阵特征值提出了Frangi滤波器：

由于图像的二阶差分对噪声非常敏感，且通常图像中包含有多种尺度的线状结构，仅使用单尺度不能很好地检测出各个尺度的线状结构。因此，可将Hessian矩阵的差分运算与高斯函数结合，通过改变高斯函数的空间尺度因子来获得不同尺度下的线状增强滤波。根据高斯函数的卷积性质可知，高斯滤波器与二阶差分图像的卷积等价于高斯滤波器的二阶导数与原图像的卷积，则Hessian矩阵中各元素的计算公式可表示为：

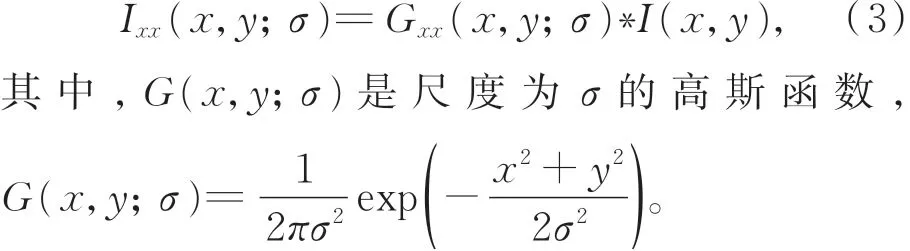
通过分析图像中目标线状结构的尺寸，设置尺度因子σ的迭代范围为[σmin，σmax]，选取在多尺度下像素点的最大响应值作为该点的输出，最后将图像中各像素点处的输出进行融合，即可得到原图像经过多尺度滤波后的增强图像，其数学表达式为：

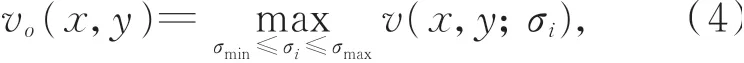
其中，v(x，y；σi)为在尺度σi下，像素点I(x，y)处的最大响应值。

2.2 支持向量机

支持向量机是在有序风险最小化的基础上发展起来的一种专门的小样本统计理论，至今已被成功应用于各种领域［14-17］。支持向量机的本质是二次型方程求最优解，其学习的基本思想是寻找一个最优的超平面，该超平面能够正确分开数据集（使分类错误率为0），且使得两类数据之间的间隔最大。

支持向量机的分类问题可分为线性可分和线性不可分两种情况，线性不可分的情况是由线性可分发展而来的。以图1中二维空间中两种数据分类为例，在图1（a）和图1（b）中，实心点和空心点分别表示两类样本，其中线性可分的情况如图1（a）所示，图中H为找到的最优分类线，H1，H2为与两类样本相切的直线，位于切线H1和H2上的样本即为支持向量；线性不可分的情况如图1（b）所示。

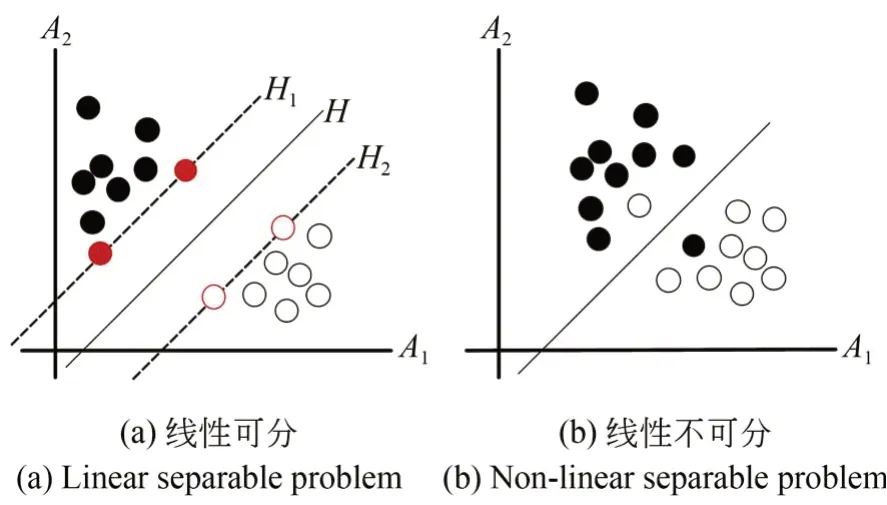
图1 简单分类问题Fig.1 Simple separation problem

2.3 灰度共生矩阵

灰度共生矩阵（Grey-Level Co-occurrence Matrix，GLCM）是在假定图像中各像素间的空间分布关系包含了图像纹理信息的前提下，提出的具有广泛性的纹理分析方法。GLCM通过统计在方向θ上间隔d的一对像素点灰度出现的统计规律来反映图像在方向、间隔、变化幅度及快慢上的综合信息。

一般不直接使用灰度共生矩阵计算，而是使用在其基础上获取的二次统计量［18］，研究发现由GLCM得到的二次统计量中仅有能量、对比度、相关性、逆差矩这4种特征是不相关的，且这4个特征既便于计算，又能得到较高的分类精度［19］，因此本文采用这4种特征来表示图像的裂纹信息，这四种特征的定义如下：

（1）能量：又叫角二阶矩，反映了图像灰度分布均匀程度和纹理粗细度。若灰度共生矩阵的元素值相近，则能量小，表示纹理细致。

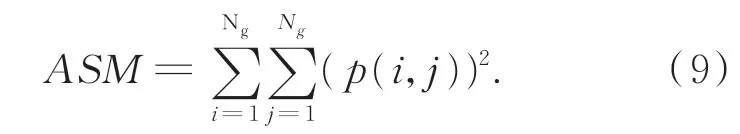
（2）相关性：反应局部灰度相关性，用来度量图像的灰度级在行或列方向上的相似程度，其值越大相关性也越大。

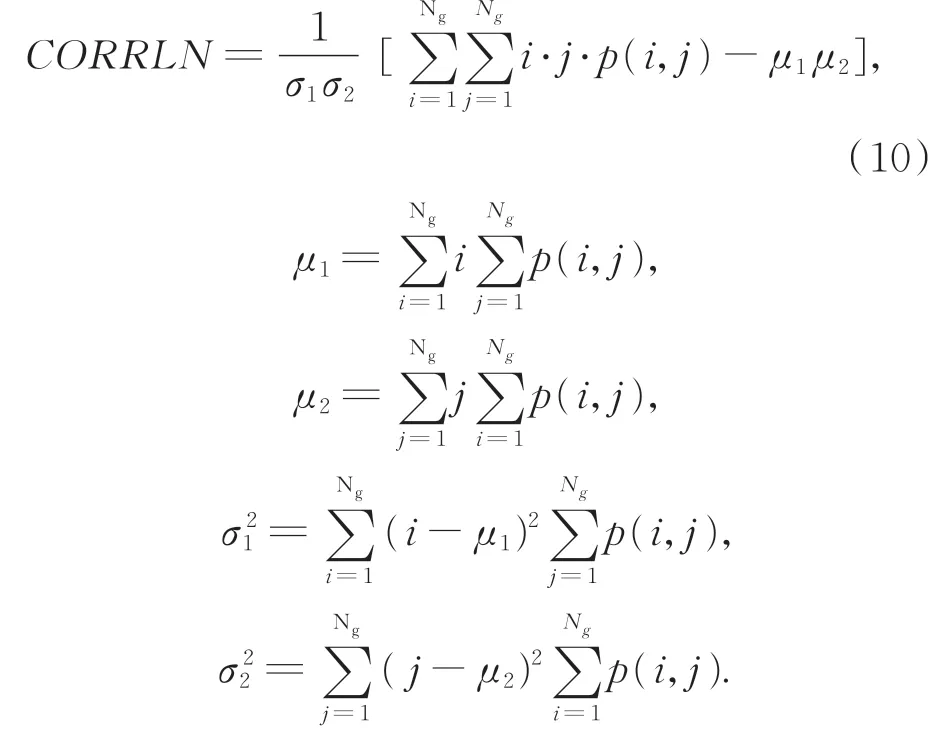
（3）对比度：反映图像的清晰程度，是图像矩阵值的分布情况和图像的局部变化，其值越大表示纹理基元对比度越强、沟纹越深、图像越清晰。

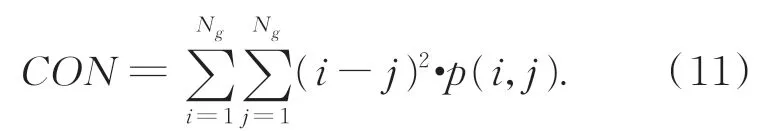
（4）逆差矩：度量图像的纹理局部变化，其值越大则图像纹理越规则。

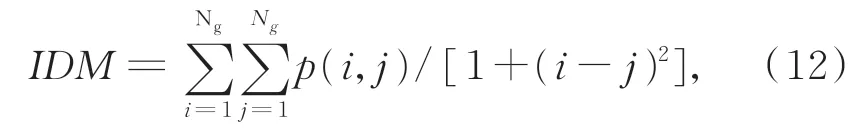
其中：p为共生矩阵，N g为共生矩阵的阶数，i和j分别表示共生矩阵的行和列，μ1，μ2表示均值，σ21，σ22表示方差。

3 基于Hessian矩阵和SVM的CT图像裂纹分割方法

基于Hessian矩阵和SVM的CT图像裂纹分割方法可分为3个步骤：（1）使用训练集图像训练SVM分类模型；（2）使用SVM分类模型定位裂纹所在的图像块；（3）使用自适应阈值分割得到裂纹。其详细步骤如下所示：

（1）训练集中的每幅图像均采用图2所示的步骤处理，其中前景区域包括工件和裂纹区域，所有的后续处理步骤只考虑前景区域内的像素点；基于Hessian矩阵的多尺度滤波方法可以获得图像中的线状结构；然后增强线状图像的对比度并分割为若干尺寸相同的小图像并按小图像中有无裂纹分为两类。当所有训练集图像均已分割为小图像并分为两类后，再使用特征提取方法提取两类小图像的特征，得到两个特征矩阵；最后选择适当的SVM参数，利用前面得到的两个特征矩阵训练SVM分类模型。

图2 图像预处理Fig.2 Image pre-processing

（2）测试图像使用图2所示的预处理步骤处理，得到若干由测试图像分割得到的小图像；再从小图像中提取与（1）中相同的特征；然后用（1）中得到的SVM分类模型对特征矩阵预测；最后将预测为无裂纹的图像块区域像素置零，其他区域像素保留不变，得到图像P1。

（3）使用自适应阈值分割方法得到图像P1中的裂纹结构。

3.1 图像的预处理

在训练SVM分类模型前，先对CT图像预处理，预处理流程如图2所示。图2中前景区域是指所有工件和裂纹区域，为了加快识别分割的速度且防止背景中的噪声对识别和分割带来干扰，前景区域之外的像素点不参与后续的计算。

由于样本图片对比度低，且存在噪声、伪影等干扰，本文在预处理阶段首先使用基于Hes⁃sian矩阵的多尺度线状滤波方法提取原CT图像中的线状结构，并对得到的线状图像进行对比度增强。

然后将线状图像分割为若干尺寸相同的小图像，以提高识别算法的正确率与处理效率，并将得到的小图像按有无裂纹分为两类。

3.2 训练SVM分类模型

训练SVM分类模型需要确定一组参数，包括SVM的类型、核函数的类型、惩罚因子等。其中核函数是支持向量机算法的核心，常用的核函数有线性核函数、多项式核函数、径向基函数（Radial Basis Function，RBF）、Sigmoid核函数。根据本文研究对象的特征，选择RBF核函数，这是一种径向对称标量函数，高斯函数是最常用的径向基函数。

与RBF核函数紧密相关的有两个参数：惩罚因子c和γ。惩罚因子在误分类样本和分界面简单性之间进行权衡，低的c值使分界面平滑，高的c值通过增加模型自由度以选择更多支持向量来确保所有样本都被正确分类。而参数γ定义了单个训练样本的影响大小，值越小影响越大。本文使用网格搜索方法获得最佳的c和γ。

3.3 定位裂纹所在图像块与裂纹分割

对测试图像进行预处理，预处理的过程如图2所示，得到线状图像P2。预处理结束后将得到N幅子图像，提取所有子图的特征向量得到由N个特征向量组成特征矩阵，再利用上一步得到的SVM分类模型对特征矩阵预测，预测结果为一个仅由元素1和-1组成的N维列向量，本文SVM训练时选择有裂纹子图像的特征矩阵为正样本，因此预测结果为1和-1分别表示对应的子图像中有裂纹和无裂纹的情况。然后只保留P2中预测为有裂纹的图像块，最后使用自适应阈值分割方法分割得到图像P2中的裂纹结构。

4 实验结果与分析

本文的实验环境是在型号配置为Inter®Core™i7-8700 3.20GHz CPU、16GB RAM、Win⁃dows10系统的计算机下，采用MATLAB结合C++语言在MATLAB 2018a平台上实现的。本文主要研究对象是钢轨CT图片与石油岩心CT图片，其中钢轨CT图像含有较严重的伪影，石油岩心CT图像中存在明显的噪声且裂纹对比度低，典型的钢轨CT图像和石油岩心CT图像如图3。钢轨CT样本共60幅，石油岩心CT样本共58幅，部分样本图像如图4。

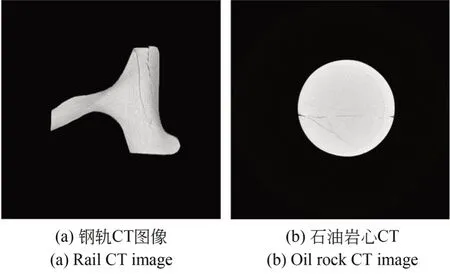
图3 工业CT切片图像Fig.3 Typical industrial CT images

图4 部分CT样本图片Fig.4 Partial sample CT images

提取并增强图3（a）、3（b）中的线状结构，结果如图5所示，可以看出：图5（a）、5（b）中较好的保留了原图中的线状结构，且裂纹处对比度较高。虽然图5（a）、5（b）中裂纹结构已比较明显，但直接使用自动阈值分割方法的话，仍会受到图中伪影和噪声的干扰，导致分割结构不佳。图5中两张样本图片使用自动阈值分割的结果如图6所示。

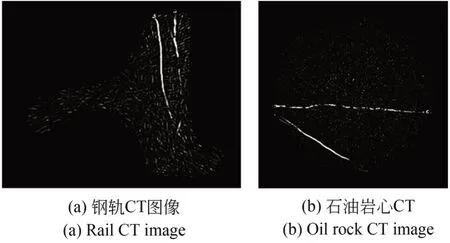
图5 形态学运算后滤波结果图Fig.5 Filtering results after morphological operation

图6 自动阈值分割结果Fig.6 Automatic threshold segmentation results

为获得更好的分割结果，本文将线状图像分割为小图像，通过判断小图像中是否含有裂纹，从而将裂纹所在的范围缩小。图7为将线状图像分割为小图像并分类的效果图。

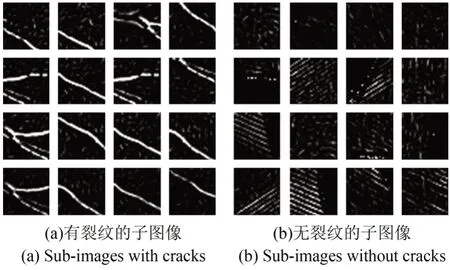
图7 部分子图像Fig.7 Partial of sub-images

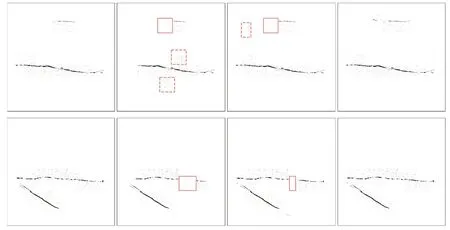
图像识别中常用的特征有：GLCM特征［20-21］、HOG特征［22-23］、Hu不变矩特征［20，24］、LBP特征［25-26］。为验证GLCM特征的有效性，分别使用以上4种特征训练SVM模型和预测，实验结果如图8所示。图8中每行的4幅图像为同一测试图像依次使用GLCM特征、LBP特征、HOG特征、Hu特征的识别效果，图（b）～（d）中虚线标记的部分为在图（a）的基础上增加的误识别的区域；实线标记的部分为在图（a）的基础上漏识别的区域。误识别指SVM分类模型将无裂纹子图识别为有裂纹子图；漏识别指SVM分类模型将有裂纹子图识别为无裂纹子图。可以看出，4种特征中，使用GLCM特征训练的SVM分类模型识别的正确率最高。

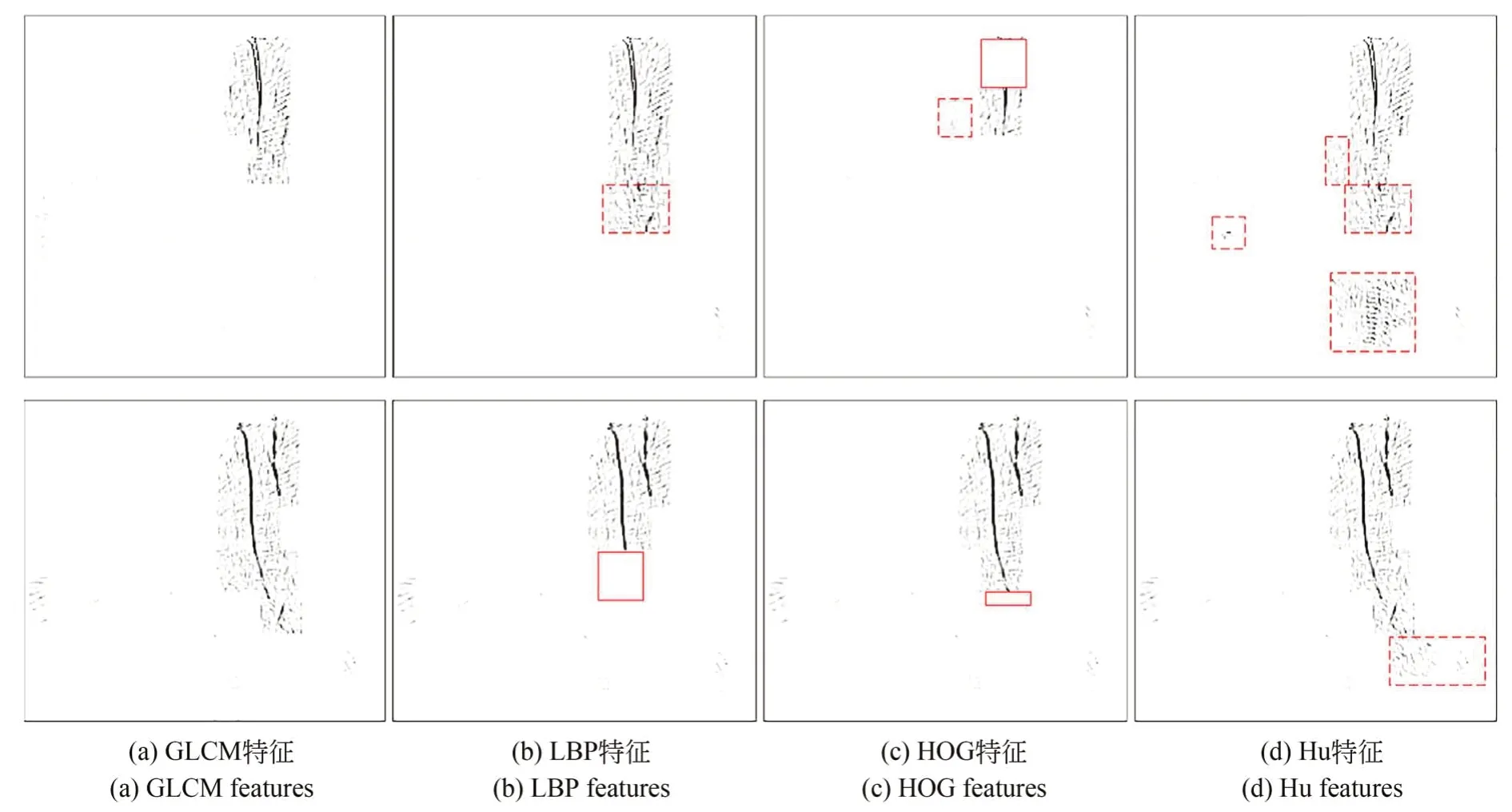
图8 不同特征识别结果Fig.8 Recognition results of different features

为验证本文分割方法的有效性，将本方法与RSF（Region-Scalable Fitting）方法、数学形态学分割、Otsu（自适应阈值分割）分割方法作对比。经实验，直接使用RSF、数学形态学、Otsu方法不能分割出图像中的裂纹，因此本文先提取并增强原图中的线状结构，再在线状图像上进行RSF、数学形态学及Otsu分割，其结果图像如图9所示。图9（a）为原图，图9（b）～9（d）分别为使用本文方法、RSF方法、数学形态学方法、Otsu方法分割的结果，图9（c）中绿色标记的区域为RSF方法分割得到的裂纹。由4组实验可以看出，当裂纹对比度低时（如第一行与第二行），Otsu方法分割完整性最差，RSF方法次之，本文方法最佳；当噪声、伪影较为严重时（如第三行与第四行），Otsu分割正确性最差，RSF次之，本文方法效果最好。且在实验过程中发现，RSF方法参数较多，需要多次手动调整获得最佳值，数学形态学方法也需要多次手动调整才能获得最好的分割效果。

图9 不同算法分割结果Fig.9 Segmentation results of different algorithms

本文定义SVM模型的识别率为SVM模型识别子图像有无裂纹的准确率，即SVM模型识别准确率=正确识别的子图像数/总子图像数×100%，其计算步骤为：首先将所有测试图像分割为小图像，然后利用SVM分类模型分类，最后统计分类结果中正确识别的子图像数量。表1为由测试集中10幅岩心CT图像与10幅钢轨CT图像计算出的SVM模型识别率。

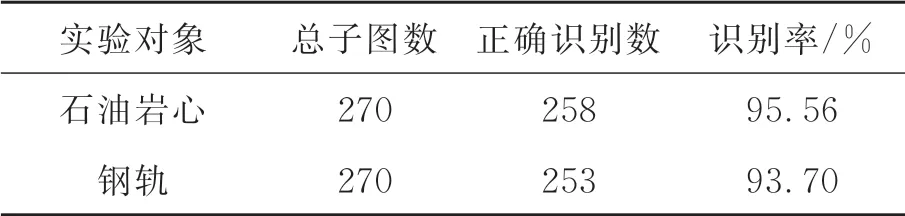
表1 不同对象识别准确率统计表Tab.1 Statistical table of different object on recognition rate

为验证本文模型的泛化能力和鲁棒性，选择了一个新的岩石CT图像作为测试样本，如图10（a）所示。新样本未出现在训练集图像中，图10中红色区域标注的区域为待分割的裂纹。使用本文方法分割图中裂纹，结果如图10（b）和10（c）所示，结果显示本文模型具有较好的泛化能力和鲁棒性。

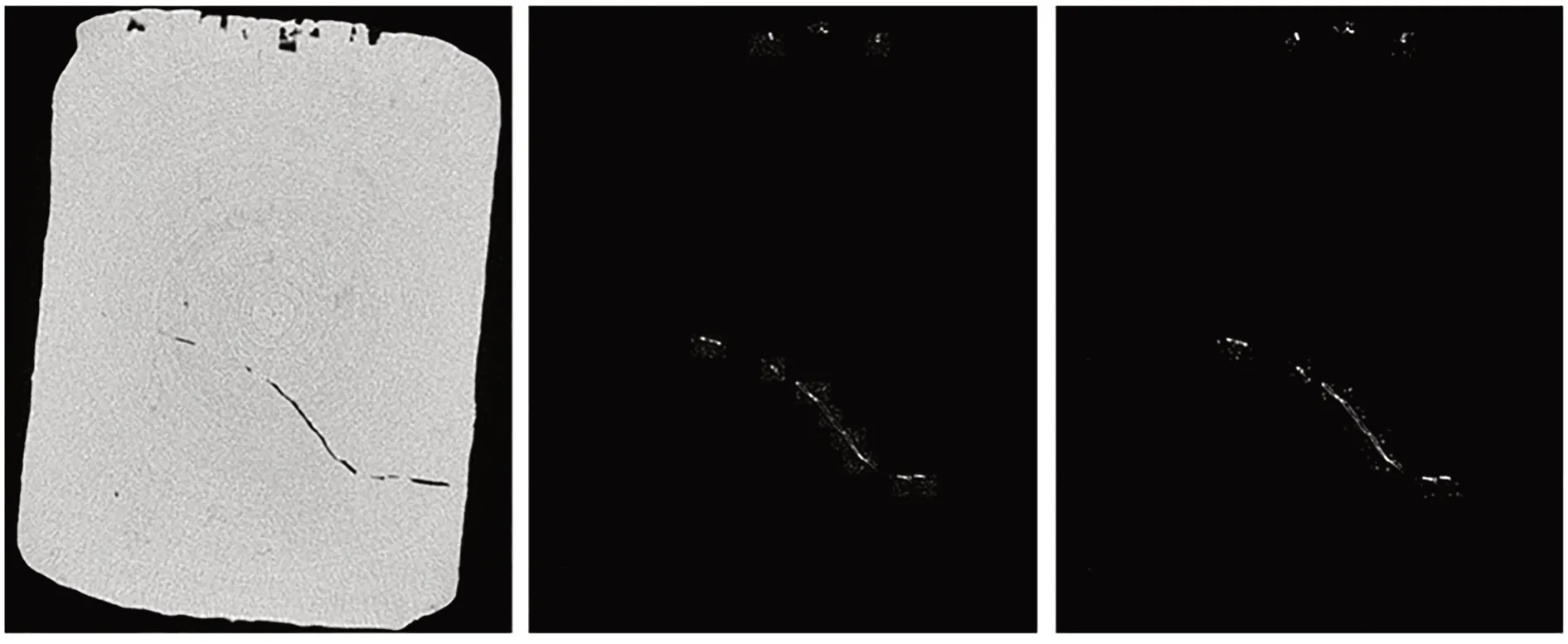
图10 模型泛化能力与鲁棒性验证Fig.10 Model generalization ability and robustness verification

实验结果表明，本文方法具有较好的抗干扰性与鲁棒性，即在图像对比度低或图像中伪影严重时，仍能获得较好的分割结果；利用SVM算法识别裂纹图像块的准确率达到了94.5%。

5 结 论

为实现CT图像裂纹精确分割，解决图像中金属伪影、噪声等干扰，本文联合基于Hessian矩阵的多尺度滤波和支持向量机的算法优势，提出了基于Hessian矩阵和支持向量机的CT图像裂纹分割方法，并对方法进行了有效性验证。基于Hessian矩阵的多尺度滤波方法可以突出图像中的裂纹结构，增加裂纹的对比度；基于SVM的分类方法可以识别图像中带裂纹的图像块。将本文方法与RSF方法、数学形态学方法、Otsu方法分割的结果进行对比，结果表明，基于Hessian矩阵与SVM的裂纹分割方法具有较好的抗干扰性且算法参数简单，图像识别率达到了94.5%，是一种有效、可行的方法，具有实际工程应用价值。