高桩码头基桩损伤的光纤光栅传感阵列识别
舒岳阶,吴 俊,周世良,王俊杰
(1.重庆交通大学 西南水运工程科学研究所,重庆400016;2.重庆交通大学 内河航道整治技术交通行业重点实验室,重庆400074;3.重庆西科水运工程咨询中心,重庆400016)
1 引 言
基桩是高桩码头最重要的承力构件,大部分位于水下。在外界不利环境和荷载的作用下,基桩会不可避免地发生性能衰退并产生损伤,若不能及时检测基桩中的损伤并消除其不良影响,损伤可能进一步演化并导致高桩码头结构失效破坏。现有的高桩码头基桩检测方法主要分为三类,即传统基桩检测方法[1-2]、基于动力的基桩损伤检测方法[3]和基于挠度的损伤检测方法[4]。
传统基桩检测方法包括静载法、钻孔取芯法、超声波法和高低应变法等[1-2]。这些方法一般用于基桩的定期检测,定性判定桩身是否存在损伤,无法准确定位损伤、以及评估损伤程度,部分方法不仅现场难以实施,检测过程还会对基桩产生损伤。
基于动力的基桩损伤检测方法,利用损伤发生前后结构动力特性参数的改变来诊断结构损伤[5],且研究成果较多[6]。在码头损伤检测方面,魏文馨[7]采用数值分析构建了基于模态的内河框架墩式码头桩、柱、撑等的损伤指标,并用神经网络对码头结构构件的损伤进行识别。孙熙平等[8-10]提出了一种适用于环境激励下高桩码头模态参数识别的ERA方法,能够比较准确地识别基桩损伤部位,但在计算模态应变能时需要有限元模型全部自由度的完整振型模态信息。基于动力的基桩损伤检测方法在实际应用中仍然无法克服模态参数识别不够精确、高阶模态难以获得、模态参数受环境因素影响大等问题。
基于挠度的静态损伤检测方法认为损伤导致结构挠度发生变化[11],目前在高桩码头中未见报道,但在其他结构损伤中有相关研究。该方法进行损伤识别的思路有两种:一种是以实测静态挠度与有限元模型计算静态挠度的差异最小化为约束条件,采用最小二乘迭代方法[12]或自适应参数分组方法[13],不断更新修正FEM模型,然后以修正后的FEM模型参数作为当前的结构参数,并与初始结构参数进行比较,从而识别损伤,但该思路计算量大,不适合工程应用;另一种是直接从挠度中提取结构损伤特征,建立挠度与损伤的关系,据此实现损伤识别,唐盛华[14]、Le N T[15]、Ma Q[16]、佟兆杰[17]等将该方法应用于简支梁损伤识别中,通过理论分析和数值计算验证了该方法的可行性。
综上,基于挠度与损伤关系的静态损伤识别方法,不需要获取结构高阶模态,也不需要复杂的有限元迭代计算,适合于工程应用。但是,在高桩码头基桩损伤检测方面却未见相关报道。其原因主要有两点,一是现有研究对象通常为简支梁,高桩码头基桩的受力特性与简支梁完全不同,尚不清楚高桩码头基桩损伤后的特征表现;二是高桩码头基桩大部分位于水下,常规挠度测量方法,如水准仪、位移计等,难以安装并测量基桩轴身的挠度变化,基于应变估计挠度的方法不适合于有损结构的挠度测量[18-21],基于光纤形状传感技术的基桩挠度监测还有待研究[22]。
针对高桩码头基桩挠度难以测量,静态损伤特征不明的问题,本文提出在基桩上对称布置两列光纤光栅(Fiber Bragg Grating,FBG)应变传感器阵列,通过该阵列监测基桩的轴向应变变化,并计算基桩挠度,从挠度中提取损伤特征,从而实现损伤识别。该方法不依赖优化算法,计算简便,可应用于高桩码头桩基的损伤检测。
2 高桩码头基桩损伤识别原理
2.1 基于光纤光栅分布式传感的基桩挠度测量方法
静态损伤检测方法认为,挠度包含了结构损伤信息,通过监测结构挠度的变化情况可判断损伤位置和程度。高桩码头基桩大部分位于水下,常规挠度测量方法难以施测。现有研究提出了一系列利用应变估计挠度的方法,Kim,N.S.[18]基于弹性力学原理,Hui Xu[19]假定挠度为多项式函数,强小俊[20]推导了竖向挠度的差分计算方法,裴华富[21]通过梁的弯曲理论公式和差分算法等分别提出了挠度估算方法。这些方法的理论基础是材料力学各向同性的假设,仅限于无损伤结构挠度的估算。光纤形状传感技术是近年来光纤传感领域一个新的研究方向[22],其原理是利用若干路在空间上具有特定排布的光纤组合在一起测量对象曲率,重构对象的形状和空间位移。该技术应用于航天结构[23]、医学检测[24]、桥梁构件位移测量[25]和软体机器人控制[26]等场合,但在高桩码头基桩这种大型结构挠度测量中的应用还有待探索。
本文采用两列光纤光栅应变传感器,对称安装在基桩桩身上,基于应变与曲率的几何关系、曲率与挠度的几何关系,实现了基桩损伤条件下的轴身挠度测量。基桩上的光纤光栅应变传感器阵列布置如图1所示,将基桩沿轴向等分为n段,每段长为Δl,采用成桩过程预植或成桩后表面安装的方式,沿基桩轴向对称布置n对光纤光栅应变传感器,任一分段对称布置的两个传感器的连线与水平作用力F平行。

图1 光纤光栅传感器阵列布置形式Fig.1 Layout of fiber Bragg grating sensor arrays
假设基桩满足梁弯曲变形的平面假设,即变形后横截面仍保持为平面且垂直于变形后的梁轴线,且沿基桩横截面高度方向上的应变呈线性分布。取基桩第i段,未损伤情况下,中性轴与梁轴线重合;若基桩产生损伤,损伤截面处的中性轴与梁轴线不重合,且中性轴位置随损伤程度的变化而变化[27],如图2所示。

图2 损伤对中性轴位置的影响Fig.2 Effect of damage on position of neutral axis
在水平力作用下,基桩第i段对称布置的两支FBG的应变值分别为:

式 中:ΔλBli,ΔλBri为 考 虑 温 度 补 偿 后 左 右 两 支FBG的波长变化,λBli,λBri分别为左右两支FBG的初始中心波长,Kεli,Kεri分别为左右两支FBG的应变系数,i=1,2,…,n。
根据几何关系,该段实测曲率κm(i)为:

其中d为基桩直径。由于挠度是曲率的二重积分,即:
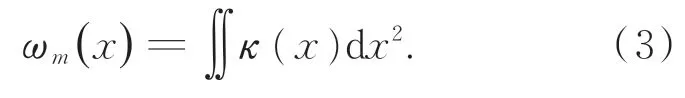
由于式(2)是离散序列,采用数值计算方法对式(2)进行二重积分,得到基桩挠度序列为ωm(i)。该方法不依赖于材料力学中各向同性的基本假设,对于未损伤基桩和损伤基桩的挠度测量均适用。
2.2 高桩码头基桩损伤的静态挠度特征
高桩码头基桩底部嵌入地基,基桩顶部与码头上部结构相连并承受三向应力作用。假设损伤测试前后基桩顶部的三向应力状态不变,在该应力状态的基础上,再施加一较小水平作用力F,基桩仍处于弹性变形阶段。根据力学叠加原理,可不考虑初始三向应力状态。此时,基桩可等效为悬臂梁。建立的基桩坐标系如图3所示,以嵌固分界面处基桩底部圆心为坐标原点,基桩轴向为x轴,基桩径向两互相垂直方向分别为y轴和z轴。水平作用力F与y轴平行。由于损伤识别不同于承载力测试,不需要加载到极限状态。损伤识别中加载的水平作用力较小,基桩力学性能保持在线弹性阶段。
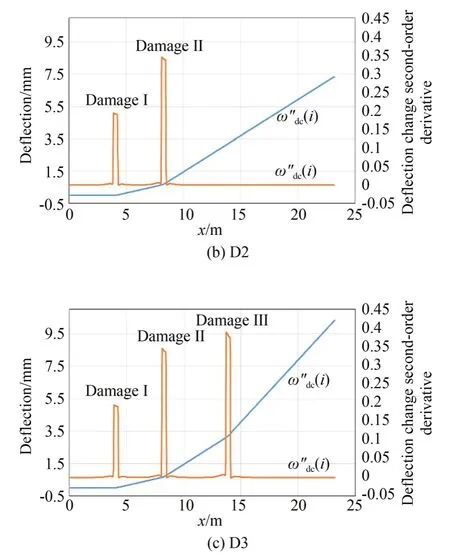
设基桩存在m个损伤,损伤位置序列为[aj,aj+bj],j=1,2,3…m,其中a1 图3 基桩坐标系与损伤示意图Fig.3 Pile coordinate system and damage diagram 一般认为,损伤导致结构抗弯刚度发生变化,损伤区域的抗弯刚度为Ej I,E j为损伤位置处的弹性模量,I为截面惯性矩,Ej与未损伤时的初始弹性模量E0的关系为: 式中αj为损伤系数。αj=1表示完全损伤,αj=0表示无损伤。 梁的挠度曲线方程为: 式中:ω为挠度,F为水平作用力,l为基桩岩土分界面以上总长。边界条件为:ω(0)=0,ω′(0)=0,且满足挠度连续性原则。根据式(5)可得无损伤条件下的基桩挠度方程为: 同样,根据式(5)及边界条件,计算损伤条件下的基桩挠度方程ωd(x)。定义挠度变化ωdc(x)=ωd(x)-ωh(x),且 设βj=αj/(1-αj),得到: 图4 基桩多损伤挠度变化Fig.4 Multi-damage deflection curve of pile 即损伤位置处的θ(x)为常数,且仅与损伤程度有关,未损伤区域为0,据此可通过θ(x)计算各个损伤的损伤程度αj。 综上,基桩损伤的挠度特征如表1所示,根据该特征,可首先利用ω′′dc(x)进行损伤定位,然后利用θ(x)进行损伤程度识别。 表1 基桩损伤的挠度特征Tab.1 Deflection characteristics of damaged piles 光纤光栅传感器阵列将基桩划分为n段,根据基桩损伤特征判断每段的损伤情况。首先,根据式(2)测量相同水平作用力下,损伤前、后基桩挠度序列分别为ωh(i),ωm(i)。则挠度变化序列(i)为: 图5 ω′′dc(i)与ω′′dc(x)的关系Fig.5 Relationship betweenω′′dc(i)andω′′dc(x) 式中Δl为基桩分段长度,同时也是传感器阵列中相邻两只传感器的间距。由式(15)可知,光纤光栅传感器阵列分布越密,损伤定位精度越高。 在确定损伤位置的基础上,采用θ(i)进行损伤程度计算,理论上每个损伤区间内的θ(i)为常数,由于测量误差的影响,实测θ(i)不是常数,以损伤区域内θ(i)的平均值计算损伤程度。设某个损伤区域分段为[j,j+k],则损伤程度αj为: 综上,高桩码头基桩分段损伤识别步骤如下: (1)在基桩轴向对称布置两列式光纤应变传感器; (2)在同一水平荷载条件下,测试初始未损伤基桩的轴向应变分布、以及损伤后基桩的轴向应变分布,并计算挠度; (5)根据式(16)确定每个分段的损伤程度。 为了验证本文提出的损伤识别方法,以重庆新生港码头嵌岩灌注桩为原型,建立了ABQA⁃US单桩损伤数值分析模型。桩长37.8 m,嵌入中风化岩层12.5 m,直径2 500 mm,C30钢筋砼嵌岩灌注桩。前排基桩钢筋笼受弯钢筋为64根直径28 mm的二级钢筋,保护层厚度80 mm;外层箍筋为直径10 mm的一级钢筋,间隔200 mm;内层箍筋为直径28 mm的一级钢筋,间隔2 000 mm。 钢筋与混凝土本构模型均采用线弹性本构模型,弹性模量分别为200 GPa和30 GPa,泊松比分别为0.3和0.2。混凝土单元类型为C3D8R,钢筋单元类型为T 3D2。桩土分界面处为固定支撑。在基桩顶部给基桩施加一个较小的水平力(120 k N),使基桩处于线弹性变形阶段。 通过减小局部区域基桩混凝土的弹性模量来模拟基桩损伤,混凝土预设损伤程度为α′。根据式(1),混凝土损伤后的弹性模量为: 式中:Ec为混凝土实际的弹性模量,Ec0为混凝土无损伤的弹性模量。 由于基桩是钢筋与混凝土的混合体,需要将混凝土预设损伤程度换算得到基桩的实际损伤程度。根据弹性模量等效原理,基桩的等效弹性模量Ea为: 式中:Es,As分别为基桩中钢筋的弹性模量和合横截面积;Ac为基桩中混凝土的横截面积。 那么基桩的实际损伤程度为: 式中Ea0,Ea分别为损伤前、后基桩的等效弹性模量。根据式(18)可将混凝土的损伤程度换算得到基桩的实际损伤程度。 依次设置了3个损伤,分别为Damage I,Damage II和Damage III,各损伤的位置及预设损伤程度α′、实际损伤程度α见表2。损伤区域的高度为0.4 m,在水平方向上贯穿整个基桩。共计算了4个工况:D0工况无损伤,D1工况包括1个损伤(Damage I),D2工况包括2个损伤(Damage I and II),D3工况包括3个损伤(Damage I,II and III)。 表2 损伤参数Tab.2 Damage parameters 每个工况计算完成后,以0.02 m的间隔,分别提取基桩左右两侧表面的应变分布,模拟光纤光栅传感器阵列测点。左侧应变提取点的坐标序列为(-1.24,0,k),右侧应变提取点序列为(1.24,0,k),k=0,0.02,0.04,…,23.2 m。计算挠度变化序列及其二阶数值微分,结果如图6所示。损伤位置处挠度变化发生转折,未损伤位置的挠度变化为直线;挠度变化的二阶数值微分在损伤位置处存在突变,与理论分析相符。 图6 各个工况的挠度变化及其二阶数值微分Fig.6 Deflection variation and its second order numerical differential under various damage cases 根据式(12)确定各工况中的损伤位置,如表3所示。计算得到的损伤位置与实际损伤位置基本相同,定位误差为0.02 m。若按照0.1 m的间隔重新提取左右两侧的应变,并计算各工况中的损伤位置,如表4所示,定位误差降低到0.1 m,与理论分析相符。 表3 计算的损伤位置与实际损伤位置的对比(间隔0.02 m)Tab.3 Comparison between calculated damage location and actual damage location(interval of 0.02 m) 表4 计算的损伤位置与实际损伤位置的对比(间隔0.1 m)Tab.4 Comparison between calculated damage location and actual damage location(interval of 0.1 m) 进一步,根据式(19)计算各个工况下不同损伤的损伤程度,并与基桩的实际损伤程度相比较,如表5所示。实际损伤程度与测量损伤程度的相对误差最大为3.3%,两者基本吻合。 表5 测量的损伤程度与实际损伤程度的对比Tab.5 Comparison of measured damage degree to actual damage degree 根据相似性原理,以重庆新生港码头嵌岩灌注桩为原型,制作了单桩结构物理模型,并进行了嵌岩灌注桩的损伤测试实验。单桩结构的模型尺寸如图7所示,模型长度比尺为20,模型桩总长1 890 mm、桩径125 mm、嵌岩段625 mm、悬臂段1 265 mm。按截面积比尺缩小原则,受弯钢筋采用8根直径为4 mm的钢筋模拟,箍筋采用间距100 mm、直径为2 mm的钢筋模拟。桩身混凝土采用M 30水泥砂浆,水泥砂浆的配比(质量比)为1(42.5R)∶1.76(砂,粒 径 为0.5~1.0 mm):0.32(水),弹性模量为17.1 GPa。实验槽长度为1.5 m,宽度为1.5 m,高度为1.2 m。地基材料采用C15混凝土模拟,材料配比为1(水泥32.5R)∶2.08(砂,粒径为0.5~1.0 mm)∶3.95(石子,最大粒径为20 mm)∶0.58(水),采用RMT-150C岩石力学实验系统测试其抗压强度为14.1 MPa。 图7 单桩结构模型Fig.7 Structure model of single pile 沿基桩轴向对称粘接16对光纤光栅应变传感器(32支),组成光纤光栅传感器阵列,布置位置如图8所示。基桩两侧FBG编号分别为LF⁃BG1~LFBG16,RFBG1~RFBG16。其 中LF⁃BG1~LFBG8、LFBG9~LFBG16、RFBG1~RF⁃BG8、RFBG9~RFBG16分别串联,同时各路再串联一支FBG作为温度补偿用。黏接胶为聚力JL-109金属焊接胶。LFBG1和RFBG1距地基表面10 cm,其他FBG间距7 cm。在实验基桩顶部和侧面安装高精度轮辐式压力传感器,分别测量水平和竖向作用力。压力传感器型号为HZC-01,精度为0.05%,过载能力为100%,量程5 t。采用反力架和千斤顶对基桩进行水平和竖向力的加载。反力架最大竖向荷载6 t,最大水平荷载1 t。 图8 模型实验桩身传感器布置示意图与现场照片Fig.8 Layout diagram and field photos of pile sensors in model test 4.2.1 FBG应变传感器的标定 FBG粘贴到基桩上后,依次施加如下分级竖向 荷 载:0(0 MPa),200(0.163 1 MPa),400(0.326 1 MPa),600(0.489 2 MPa),800(0.652 2 MPa),1 000(0.815 3 MPa),并记录各个FBG的中心波长,计算各级荷载所对应的理论应变,以此对各个FBG进行标定。 4.2.2 无损伤时轴向应变分布测试 在基桩顶部施加水平荷载300 N,测量无损伤状态下的基桩轴向应变分布。该水平力较小,以保证基桩混凝土材料处于线弹性阶段。 依次制造不同尺寸的损伤,并测试各损伤工况下的轴向应变分布。施加的水平荷载仍为300 N。通过在基桩表面水平钻孔的方式模拟基桩损伤,共制造了6个损伤(Damage 1~6),孔口位置、孔深和孔径如表5所示。其中,Damage 1与Damage 2,Damage 3与Damage 4,Damage 5与Damage 6在同一截面上对称布置。由于难以建立孔洞与刚度损失之间的直接对应关系,定义横截面损伤系数η: 式中:d为孔洞直径,h为孔的深度,D为基桩直径。以该参数表征孔洞对基桩造成的损伤程度。各个损伤的η值见表1。 测量工况总共有S0~S6 7个,其中S0工况中无损伤,S1工况中的损伤包括Damage 1,S2工况中的损伤包括Damage 1和Damage 2,…,S6工况中的损伤包括Damage 1~Damage 6。 表6 损伤参数Tab.6 Damage parameters 计算S1~S6工况下的挠度变化及其二阶数值微分,结果如图9所示。受光纤光栅应变传感器测量误差的影响,无法从挠度变化中明显分辨出损伤位置,但挠度变化的二阶数值微分在损伤位置处存在突变,据此可以判断损伤的位置,各个孔洞的真实轴向位置(距地基表面的高度)与识别的损伤位置如表7所示。孔的位置位于识别的损伤范围之内。由于应变传感器布设间隔为7 cm,因此损伤定位分辨率为7 cm。然后,计算各个工况下所有损伤断面(包含1个或两个孔洞)的损伤程度,并与式(20)计算得到的断面损伤系数进行比较,如表8所示。测量得到的损伤程度α与横截面损伤系数η之间的关系曲线如图10所示,两者呈线性关系,说明本文提出的方法可对损伤进行定量评估。 图9 各个工况的挠度变化及其二阶数值微分Fig.9 Deflection variation and its second order numerical differential under various damage cases 图10 损伤程度与横截面损伤系数的关系Fig.10 Relationship between damage degree and cross section damage coefficient 表7 损伤真实位置与识别的位置Tab.7 Real location and identified location of damage 表8 损伤程度的计算结果T ab.8 Calculation result of damage degree 本文针对高桩码头基桩的损伤识别,提出采用对称布置的两列光纤光栅传感器阵列,通过该传感器阵列监测基桩结构的轴向应变变化,并计算基桩挠度,从挠度中提取损伤特征,从而实现损伤识别。理论分析表明,利用两列对称布置的光纤光栅传感器阵列,可得到水平作用力下的基桩挠度变化,对于损伤前、后的基桩均适用。基桩挠度在损伤前后具有显著变化特征,挠度变化的二阶导数可用于损伤定位,挠度变化的二阶导数与未损伤挠度变化的二阶导数之比可用于损伤程度计算。数值计算结果与理论分析基本相符,损伤程度的相对误差最大为3.3%,损伤定位分辨力与光纤光栅应变传感器的间距相等。物理模型实验表明,受测量噪声的影响,光纤光栅传感器阵列得到的挠度变化在损伤位置未出现明显的转折,但通过挠度变化的二阶导数仍然能够检测到损伤位置,实测损伤区域与预设损伤(孔洞)的位置相符,且实测损伤程度与截面损伤系数呈线性关系,线性度达到0.887 5。本研究对于高桩码头和类似工程中基桩的损伤识别具有重要意义。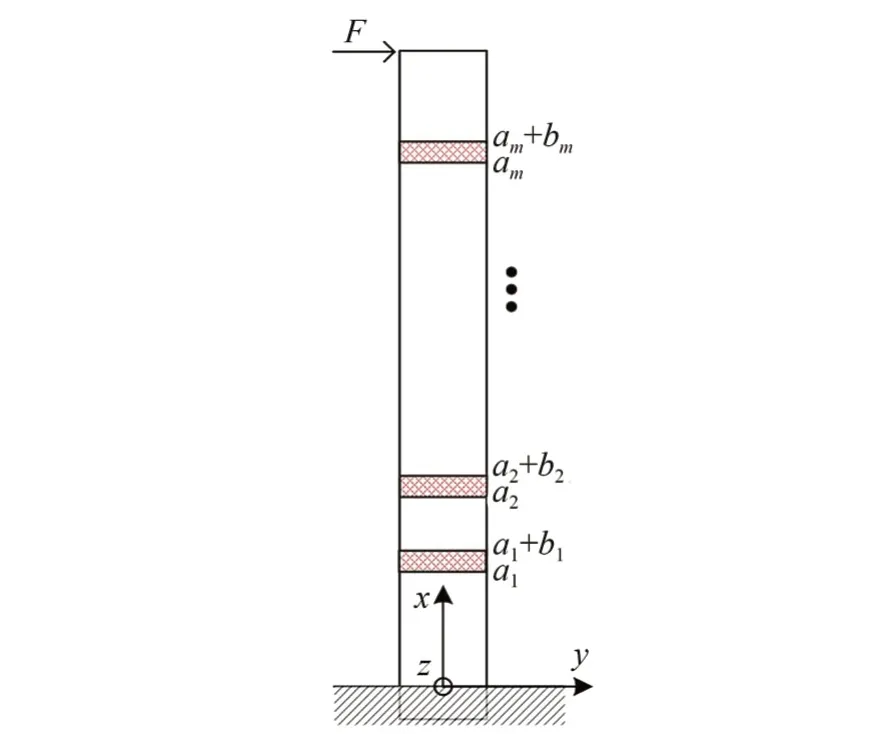
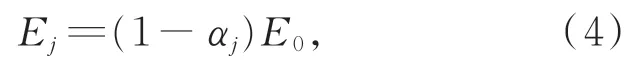
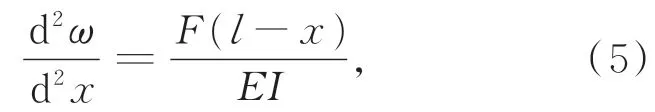
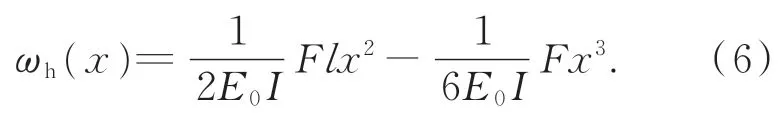


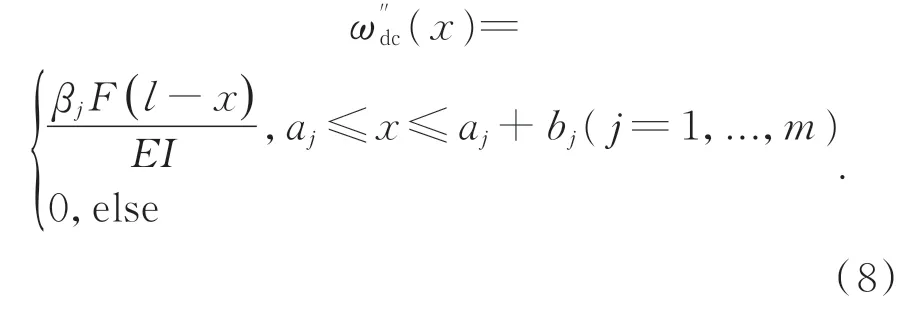


2.3 高桩码头基桩分段损伤识别




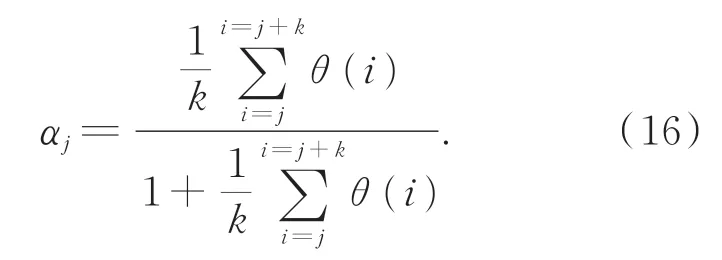
3 数值模型实验验证
3.1 有限元数值模型
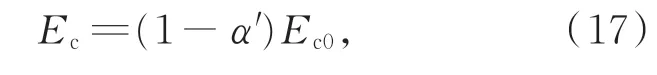



3.2 实验结果与分析




4 实 验
4.1 基桩结构模型


4.2 实验过程


4.3 实验结果与分析




5 结 论

