双波长离轴数字全息成像技术研究
葛 磊, 文永富*, 程灏波
1. 北京理工大学光电学院, 北京 100081; 2. 北京理工大学深圳研究院, 广东 深圳 518057
数字全息显微术(digital holographic microscopy,DHM)是数字全息术中非常重要的应用,它可以实现对物体三维形貌的定量、无损伤、非接触、快速、全视场观察,是一种新型光学显微术[1-3]。传统的DHM通常使用单一波长来记录目标物体的全息图,这对于表面光滑或表面光学高度不超过一个波长的物体特别有效。当物体的光学厚度大于一个波长时,由于提取相位信息时引入了反正切函数,其重建的相位图分布在[-π,π]之间,形成包裹相位。通常,需要相位解包裹算法来获得明确的相位图[4]。
常见的数值相位解包裹算法有基于可靠性的相位解包裹[5]、最小范数法和最小二乘法相位解包裹等[6]。而且,当前数值解包裹算法都存在一定的问题,计算复杂耗时,当被测物体本身有间断或者表面梯度很大时,数值解包裹算法可能引入不可预料的误差,影响重建像的空间分辨率与时间分辨率,很难实现准确的三维成像[7]。为了解决这些问题,人们提出了双波长数字全息技术[8-19],该技术可以获得具有更长的合成波长相位展开图。双波长数字全息显微术是用两个不同波长的激光进行记录,分别获取每个波长对应的相位图,再求出两者的相位差,即为等效波长的相位图。如果两波长合成的等效相位图大于经过物体的最大光程差,则可以直接获得物体真实连续的相位分布,而无需进行相位解包裹运算。由于合成波长比两个单一波长中的任何一个都长,这种方法大大扩展了测量的相位范围。
本文提出了一种结合二向色镜的可调离轴配置的双波长离轴无透镜全息成像系统,以记录双波长全息图,包括一次拍摄中不同波长的两个空间载波频率。该系统对于双波长全息图中两个载频的调整是灵活的,特别适用于需要根据物体空间频谱选择载频的情况。由于同时记录两个波长信息,且无需复杂的相位解包裹计算,该系统也可对三维物体进行实时测量。首先,本文介绍了双波长离轴全息记录和重建原理;其次,双波长相位解包裹进行数值模拟;最后,将该系统分别对相位型物体和振幅型物体进行实验测量,结果表明本文所提出的光路系统在测量微米级高度和阶跃型物体具有一定优势,且结构简单、调整灵活。
1 基本原理
1.1 离轴全息成像原理
在全息记录过程中,假设物光和参考光为平面波,其分别可以表示为
O(x,y)=o(x,y)exp[jφo(x,y)]
(1)
R(x,y)=r(x,y)exp[jφr(x,y)]
(2)
式中,o(x,y)、r(x,y)分别表示物光波和参考光波的振幅分布,φo(x,y)、φr(x,y)分别表示物光和参考光的相位分布。被测物体的物光波和参考光波在CCD上进行干涉,形成干涉全息图,其干涉条纹的强度分布见式(3)。
IH(x,y)=(O+R)2
=|O|2+|R|2+2·|O·R| cos(Δφ+x·ksinα)
(3)
式中,IH(x,y)为CCD上记录的全息图,Δφ为物光和参考光的相位差,k=2π/λ为波数,α为物光和参考光的离轴干涉角。被测物体的物光波和参考光波的干涉分量为式(3)第3项,对应频谱的±1级,包含了物光波的振幅和相位信息。
同样,当采用双波长(λ1和λ2)同时记录时,CCD上获得的干涉强度可用式(4)描述。

(4)
式(4)中的第3项和第6项分别表示被测物体的物光波与参考光波(λ1)的干涉分量和参考光波(λ2)的干涉分量,即分别对应λ1频谱的±1级和λ2频谱的±1级。
得益于离轴干涉装置,离轴记录的数字全息图可以实现频谱分离,即“零级像”和“孪生像”能够分开,因此也可以获得更好的再现像质量。假设被测物体的最大空间频率为fM,那么离轴记录时参考光和物光的夹角α应该满足以下条件:
sinα=3fMλ
(5)
在全息再现过程中,可以通过算法将被测样品的全部信息恢复出来。全息再现算法有菲涅耳积分变换法、卷积法、角谱法等,本文采用角谱法对全息图重建,由于其在推导过程中不存在限制近似条件,故该方法可以实现对衍射光波的准确描述。角谱算法对全息图重建得到的物光波复振幅分布为
(6)
式中,fx=x/λd,fy=y/λd,d为再现距离,λ为波长,F{·}、F-1{·}分别表示傅里叶变换和傅里叶逆变换。
最终再现像的光强和相位分布为
I(x,y;d)=|O(x,y;d)|2
(7)
(8)
式中,Im表示取复振幅的虚部,Re表示取复振幅的实部。
1.2 双波长相位解包裹
由于在提取相位信息时引入了反正切函数,因此当样品的高度或经过物体的最大光程差大于入射光的波长时,会产生2π模糊,即相位会包裹在[-π,π]或[0,2π]之间。为了获得样本的准确相位,需要对相位进行解包裹[4]。本文将双波长技术用于相位解包裹。当样品的台阶高度大于单个波长时,引入了合成波长,在该波长处计算物体的高度。通过使用合成波长技术,不需要额外的相位展开算法,如图2、图3所示。该技术可以显著减少计算时间并避免相位解包裹算法带来了一些问题。
双波长相位解包裹方法的实质是通过两个波长的相位图相减得到新相位图,新相位图相当于由一个更大的等效波长所得到的,因此当物体的光学高度小于这个等效波长时,相位图将不再出现包裹。以反射式装置为例,假设物体的高度为h,那么对于波长λi记录下的数字全息图,数值重建得到的相位分布可以表示为
(9)

在全息重建中,包裹相位通常是由于测量的光学高度大于一个波长而引起的。当mi的值大于零且不确定时,单波长相位图中总是存在相位模糊,因此必须通过一些相位解包裹算法来解决。根据双波长数字全息成像原理,如果合成波长Λ大于样品的光学高度,则可以通过减去两个包裹的单波长相位来获得解包裹相位[9-11,20,21]。合成波长可用式(10)表示,展开的相位图φΛ由式(11)计算。
(10)
(11)
双波长相位展开实际上取决于合成波长的值。需要注意的是,如果合成波长小于待测样品的光学厚度,则仍然存在相位模糊。这意味着两个波长之间的差异太大而无法实现相位解包裹,在这种情况下|m2-m1|>0。当两个单波长包裹相位的差值为负值时,需要加2π来求解相位跳变,此处为|m2-m1|=1。例如,在下面的第一个实验中,两个波长(450 nm和635 nm)的合成波长为1.54 μm,小于要测量的磁流变抛光得到的光学表面深度,因此会有残留的包裹相位。但在第二个实验中,合成波长远远大于USAF分辨率表面图案镀铬的厚度(约90 nm)。
由式(11),待测物体的高度可以表示为
(12)
式(12)中的相位差即相当于用等效波长Λ获取的相位。显然,等效波长Λ要比λ1和λ2大,而且λ1和λ2相差越小,Λ就越大。因此,只要选取合适的λ1和λ2,保证Λ大于物体表面光学高度,通过双波长相位解包裹就能得到展开的正确相位。双波长相位解包裹具体流程如图1所示。
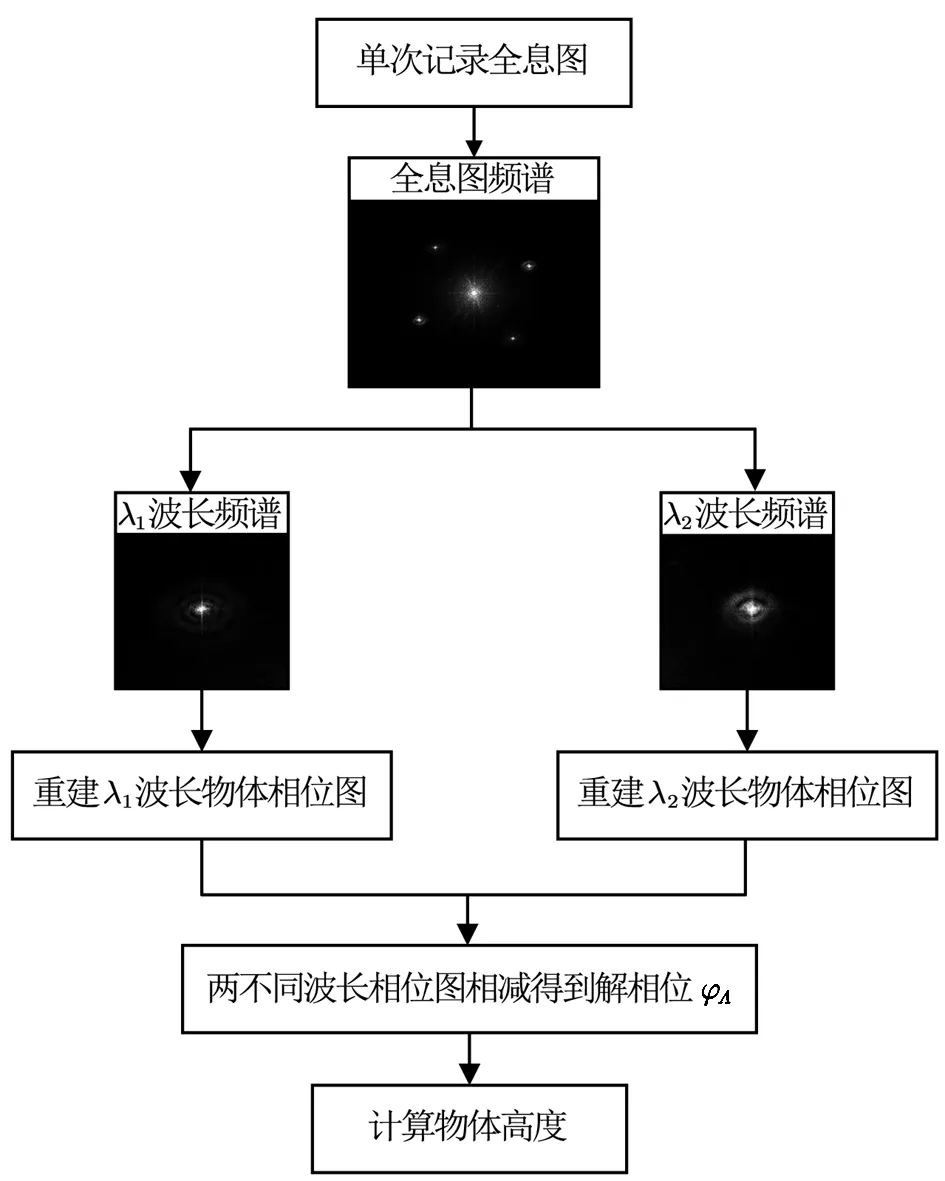
图1 双波长离轴全息无透镜成像相位解包裹流程图
2 数值模拟
数值模拟采用的两个波长分别为λ1=450 nm和λ2=500 nm,可以计算得到其合成波长Λ=λ1λ2/|λ1-λ2|=4.5 μm。首先,模拟复杂的反射式高斯面[I(x,y)=0.12*peaks(1024)],物体高度和深度均在1 μm左右,那么光经物体表面反射后产生的最大光程约为4 μm,其值超过λ1和λ2两个波长,但小于合成波长Λ。因此,利用双波长技术,无需对该物体进行相位解包裹即可恢复其真实的相位信息,如图2(c)所示。同样,如果光经物体表面反射后产生的最大光程差超过了合成波长,那么利用双波长技术得到的仍是包裹相位。其次,数值解包裹算法可能对表面梯队很大的物体失效,因此这里对倾斜阶梯型物体双波长相位解包裹进行了数值模拟,如图3所示。此倾斜阶梯型物体高度为0.8 μm,从图3(a)、图3(b)中可以明显地看到相位的包裹。对两个波长的包裹相位进行相减,得到合成波长相位图,即图2、图3(c)所示。可以看到相位已完全展开,不再有包裹。这是因为,模拟样本的光学高度小于合成波长,两波长的包裹相位相减后不会有相位间断,即相减过程中没出现负值,因此也无需对出现的负值补偿2π。图2、图3(d)为被测物体的双波长解相位后重建的三维高度图。

图2 双波长相位解包裹数值模拟复杂高斯表面(所有图像像素均为1024×1024)(a) 450 nm波长得到的相位图; (b) 500 nm波长得到的相位图; (c) 合成波长的相位图像; (d) 物体的三维分布

图3 双波长相位解包裹数值模拟倾斜阶梯型物体(所有图像像素均为1024×1024)(a) 450 nm波长得到的相位图; (b) 500 nm波长得到的相位图; (c) 合成波长的相位图像; (d) 物体的三维分布
通过重建的三维高度图可以直观地看出双波长解相位可以拓展测量范围,相较于单波长(可见光)一般测量范围在400 nm,双波长测量可以将范围拓展3~10倍,甚至更多。且该过程没有复杂的计算、计算量小,是较为理想的解包裹算法。
3 实验装置
为了验证双波长离轴全息无透镜成像系统的可行性,实验采用反射式离轴数字全息系统。两个用于记录的激光器分别为λ1=450 nm和λ2=635 nm的半导体激光器,根据式(10)计算可得两波长的合成波长为Λ=1.54 μm。所用CCD为黑白相机,其分辨率为2592×1944,像素尺寸为2.2 μm×2.2 μm。实验装置如图4所示。

图4 双波长离轴无透镜全息成像系统示意图
两激光器发出的激光经非偏振分光棱镜BS1后合为一束,保证两个波长的激光传输路径严格一致,之后经过聚光镜(L1,f=30 mm)和准直镜(L2,f=50 mm)进行扩束准直,中间采用视场光阑减少杂散光。光束准直后由物镜(25×0.65NA)进行傅里叶变换,经过小孔滤波后由L3(f=50 mm)进行傅里叶逆变换。准直光束经分束器BS2分为两路,一路照射样本,一路照射二向色镜(透射带370~480 nm,反射带520~610 nm,HGSP-500-D25,广州恒洋电子科技有限公司)。物光由样本反射后经分束器直接投射到CCD(daA2500-14 μm,Basler)上,参考光由二向色镜分为两条彼此分离的光路:两条各含一个波长的参考光光路,通过调整M1和M2在两个波长中引入正交的载波。两个波长参考光均以不同夹角与物光形成离轴干涉,干涉图样如图5(a)所示。图5(b)显示了双波长全息图的频谱。λ1和λ2的+1级频谱分别用蓝色和红色方框标记。为了重建双波长全息图,可以选择不同波长的+1阶频谱,然后利用角谱法再现,得到原始物波场Eo1和Eo2,其强度图分别为图5(c)和图5(d)。为了减少λ1和λ2之间的串扰,一般调整干涉条纹方向使其正交干涉,如图5(a)所示。

图5 磁流变抛光表面全息图和重建强度图(a) 双波长离轴数字全息图; (b) 对应(a)的傅里叶频谱; (c)、(d) 分别为对λ1=450 nm和λ2=635 nm的重建强度图
4 结果与讨论
以下所有结果均根据图1所示的数值重建流程获得。图6(a1)显示了λ1=450 nm的磁流变抛光表面的重建包裹相位图。利用离散余弦变换(DCT)进行相位展开操作,展开的相位图如图6(a2)所示,其中相位范围扩展到[-25,5](单位:弧度),样品的三维表面形貌如图6(a3)所示,对应的高度分布曲线如图6(a4)所示。从图6(a1)~图6(a4)可以看出,样品并非光滑的,具有圆环形的凹陷。根据式(9),样品的真实深度可以计算为h=(φ·λ)/4π。
图6(b1)~图6(b4)显示了λ2=635 nm重建的包裹相位、展开的三维相位图、三维高度图和对应的高度分布曲线。由于λ2相比λ1更大,其包裹相位条纹显得较为稀疏,如图6(b1)所示,其中相位范围扩展到了[-15,5](单位:弧度)。可以看到的是,相比较图6(a3)物体的三维高度,图6(b3)无明显变化。但样本测量时噪声的存在,一定程度影响了测量精度,同样干扰了后面双波长重建的效果。主要原因是,未对样本进行预处理,例如去倾斜和去除背景。
图6(c1)显示了Λ=1.54 μm重建的包裹相位图。可以看到,相较于图6(a1)和图6(b1)中6个包裹相位环,图6(c1)中仅有2个包裹相位条纹。图6(b2)和图6(b3)为相位展开的三维图和物体三维高度图,其中相位范围拓展到[-17,7](单位:弧度),对应的高度分布曲线如图6(c4)所示。
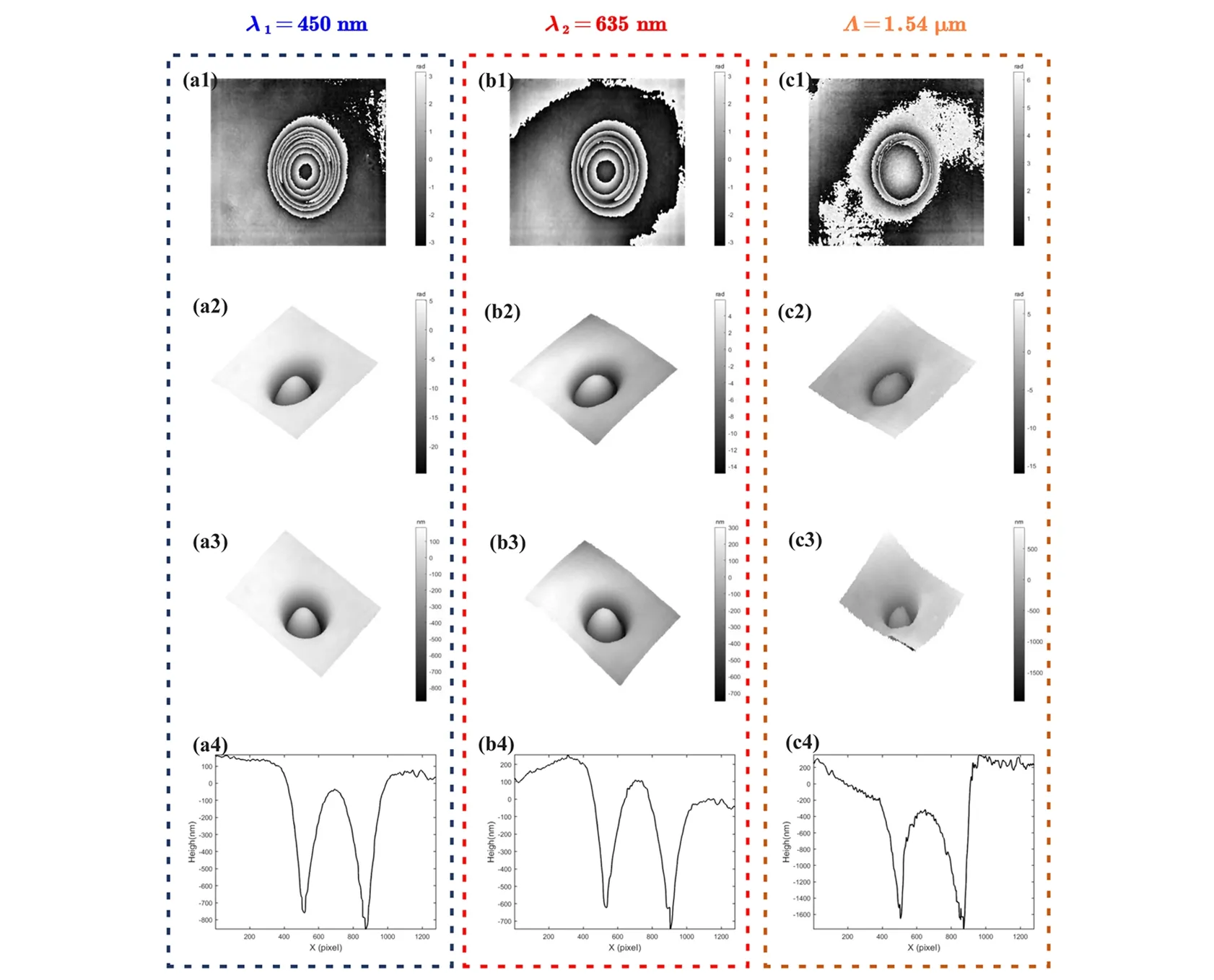
图6 磁流变抛光表面测量结果(a1,b1,c1)分别为λ1、λ2和Λ重建包裹相位图;(a2,b2,c2)分别为λ1 、λ2和Λ重建的解包裹相位图;(a3,b3,c3)分别为λ1、λ2和Λ重建三维高度图;(a4,b4,c4)分别为λ1 、λ2和Λ重建高度分布曲线
需要注意的是,当合成波长仍小于物体高度或者经过物体的最大光程差时,双波长技术解相位得到的仍是包裹相位。因此,人们希望合成波长尽可能大,这样即可避免解相位的问题。根据式(10),增大合成波长意味着减小|λ1-λ2|的值。然而当λ1和λ2之间差值过小会造成如下问题:一方面,系统对二向色镜的规格要求更高,容易造成两波长之间的串扰,加重级次的重叠伪影,从而降低重建像的分辨率;另一方面,随着合成波长增大,对应的测量噪声也会相应放大。从图6可以看到,图6(c1)~图6(c4)比图6(a1)~图6(a4)和图6(b1)~图6(b4)有着更多的相位噪声。事实上,这是因为在计算合成波长的过程中,物光O1、O2中的相位噪声同样被放大了,尽管测量的深度得到了极大的拓展。因此,具体操作时,一般先评估样本的高度,再选择合适的双波长数字全息系统进行测量。或者,先标定双波长系统的测量误差,然后在重建时,利用软件对测量误差进行补偿。
图7显示了USAF 1951分辨率板的测量结果。λ1和λ2重建的包裹相位分别为图7(a1)和图7(b1),与之相对比的合成波长Λ的相位为图7(c1)。可以看到,合成波长的相位图已没有包裹相位。在折射率或梯度分布较大的情况下,这更便于样品的相位展开操作。图7(c3)显示了从合成波长获得的样品表面形貌,结果与从λ1和λ2单波长获得的结果基本一致,但多了很多噪声。这是因为,双波长技术在扩展了测量范围的同时,也同步放大了噪声。对于高度在100 nm左右的样品,采用双波长技术时需注意噪声的放大问题。例如,当λ1=500 nm和λ2=502 nm差距只有2 nm时,虽然可以获得足够大的合成波长(Λ=125 μm),但噪声也会放大Λ/λ1倍,即在单波长测量的1 nm的噪声也会变成250 nm的噪声,这对测量只有100 nm高度的样本误差是致命的。因此,在实际测量过程中,尤其需要注意双波长噪声的问题。因此,我们可以采取以下措施来降低噪声放大的影响:首先,可以在系统中添加旋转毛玻璃或者选择低相干光源照明,降低系统的相干噪声;其次,预估测量样本的高度,选择合适的双波长以得到与物体高度大致匹配的合成波长;最后,对双波长全息系统的测量误差进行标定,在后续重建时对测量误差进行补偿。

图7 USAF分辨率板测量结果(a1,b1,c1)分别为λ1、λ2和Λ重建包裹相位图;(a2,b2,c2)分别为λ1、λ2和Λ重建解包裹相位图; (a3,b3,c3)分别为λ1、λ2和Λ重建三维高度图;(a4,b4,c4)分别为λ1、λ2和Λ重建高度分布曲线
5 总结
我们提出了一种基于二向色镜分光的反射式双波长离轴无透镜数字全息显微系统,可以单次采集两个离轴干涉图,拓展测量深度且无需相位解包裹运算。结果表明,该系统可以有效克服传统相位展开和重建算法在微结构成像中的局限性。该结构不仅可以提高全息图的频谱利用率,也大大减少了两个波长之间的串扰,且方便引入载波,调整简单。由于双波长技术在拓展测量深度的同时也会放大相位噪声,因此双波长测量时相位噪声的抑制就很有必要。例如,后续可以采用旋转毛玻璃来进一步降低相干噪声,或者采用低相干光源照明。

