基于VMD-GST的TEO的煤矿供电线路单相接地故障测距方法

田锦绣，崔迎春，付 昱

（1.潞安化工集团有限公司李村煤矿，山西长治 046000；2.国网白城供电公司，吉林白城 137000；3.辽宁工程技术大学电气与控制工程学院，辽宁葫芦岛 125105）

0 引言

煤矿电气化的发展极大地推进了煤矿产业，但也导致其供电系统日益复杂，各种煤矿井下供电线路犬牙交错［1］，使得系统在实际运行期间，易发生各种线路故障问题［2］。然而，煤矿井下的供电线路处在积水、烟雾等极其恶劣的环境下［3］，使得井下供电线路的故障定位更难确保精确度和可靠性［4］。我国煤矿井下供电线路故障定位的发展较缓，大多依旧采用井下工人查找定位故障［5］，这使得工人的安全难以得到有效的保证，且人工查找存在故障效率低、定位困难大以及可靠性差等现实问题。因此，煤矿井下供电线路的快速、准确定位于煤矿产业的安全运行具有深远的意义。

国内、外煤矿井下供电保护的相关研究者对供电线路故障定位成果内容，大致可分为阻抗法和行波法。覃剑等［6］和Q Shi等［7］利用线路两端电压分布规律，定位故障位置，该类方法无需两端数据通信，但其易受过渡电阻和线路参数不对称的影响较大，导致该方法的测距精度较低。P C Fernandes等［8］将行波分为零模与线模分量，并将上述两个分量的波头到达时间之差以此来确定故障位置，但该方法要以零模分量波速为唯一确定值的情况下才能得以保证，这也就使得该方法的适用性较差。

国内、外对煤矿井下供电线路故障定位的研究存在着各种各样的不足，且该问题制约着煤矿工业的发展。因此本文针对上述煤矿井下定位方法的各种不足，提出基于VMD-GST-TEO的故障定位方法，能快速、可靠地定位煤矿井下供电线路的故障，能有效保证故障地快速定位，为煤矿的安全发展奠定了坚实的基础

1 故障行波在供电线路的传播

对煤矿井下供电线路分析时，常用均匀分布参数线路［9］，如图1所示。

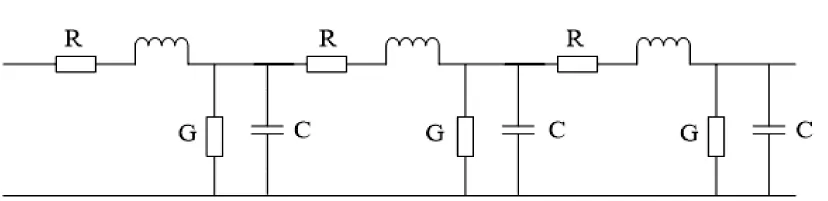
图1 供电线路分布参数

因均匀分布参数线路难以定量分析行波的变化［10］，因此本文将分布参数线路相应地化简（即不再考虑分布参数线路中的电阻和电导），即可定量且清晰地对故障传输行波过程进行分析，由均匀分布参数线路简化后的无损线路如图2所示。将图中的线路的电压u与电流i通过偏微分方程进行联立并求解，可以得到：

图2 无损线路分布参数

由式（1）可知，电压和电流行波分量在供电线路的传输过程中与将实际的行波波速有着密切的关系，因此，对行波的分析需要建立在波速固定的情况下，据此本文规定行波的波速为v＝2.98×105km／s。

图3所示为煤矿井下供电线路的简化电路，当故障行波在供电线路中传播时，因变压器对行波存在阻挡作用，因此在本文分析中变压器即可等效成开路，由于各支路与主干路之间由变压器连接构成，所以仅能分析主干线的故障行波，而无法分析支路的故障行波。因此本文的故障定位仅适用于煤矿井下供电线路的主干线。

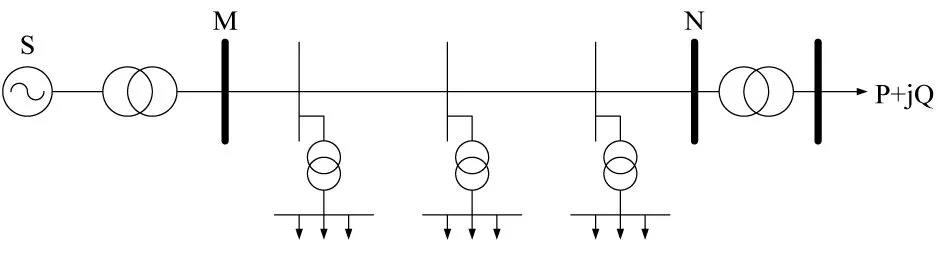
图3 煤矿井下输电线路结构

2 基于VMD的故障行波分解

故障初始行波含有大量的干扰信号，使得对其的分析将受到巨大的影响。采用VMD算法对初始故障行波进行分解，可不受其干扰信号和频率的影响，所以可以得到清晰的局部特征信号且拥有较强的鲁棒性，同时VMD相应于其他处理算法，可更好地避免端点效应。

VMD算法的目标函数是模态分量的带宽之和。VMD算法构造变分问题的具体步骤有以下3步：首先由Hilbert变换将初始故障信号f分解成若干个模态函数uk（t）；再将上述处理的模态函数uk（t）所固定的单边频谱转换到基频带中，同时计算出模态函数的中心频率e－jωkt；最后得出解调信号梯度的平方范数，估计各模态信号带宽。综合上述，VMD的约束变分问题的表达式为：

式中：｛uk｝＝｛u1，…，uk｝，为初始信号经VMD所分解得到的K个IMF分量；｛ωk｝＝｛ω1，…，ωk｝，为上述各分量的频率中心。

再通过拉格朗日乘法算子λ（t）和二次惩罚因子α，将式（2）的约束问题转变为无约束问题，即增广拉格朗日表达式，如式（3）所示：

为便于分析，本文构造煤矿井下供电线路单相接地故障时暂态行波信号，如式（6）所示，其波形如图4所示。

图4 原始信号波形

将式（6）表示的故障信号经K＝3层的VMD算法分解成3个独立的模态分量，如图5所示。

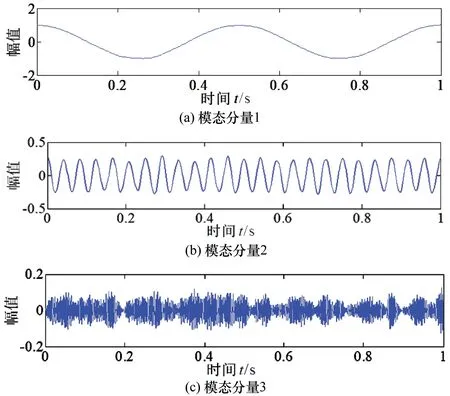
图5 K＝3时的模态分量

将图4和图5相比较，可知图5中的模态分量一与图4构成的原始信号最为相近，且当K＝3时，信号的频谱如图6所示。由图可知，当VMD的分解层次为K＝3时，分解的模态分量中的频谱图由高、中、低等频率分量波峰构成，且各个频率段中的波峰有着显著的区别，不易混淆，分解的效果好，能保存较多的原始信号特诊，因此模态分解个数取K＝3。

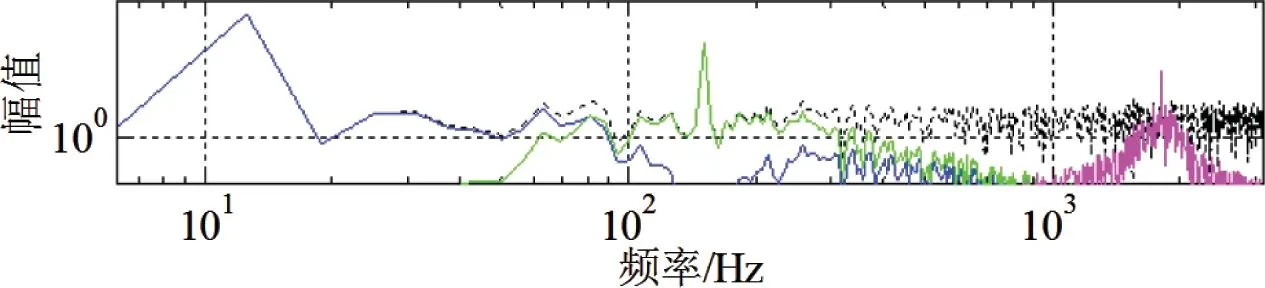
图6 K＝3模态分量频谱

3 故障行波波头的标定

前小节分析故障行波经由经K＝3的VMD分解得到3个不同的模态分量，但受制于VMD算法的本质，仅依靠VMD算法将无法识别波形的突变点，而初始行波的波头检测对于供电线路故障的定位具有巨大的意义。因此需进一步将VMD分解后的模态分量再进一步采用广义S变换来处理，以得到固定频率段的信息，以便于Teager能量算子法能可靠地对故障行波的波头进行标定。

3.1 广义S变换

常规的S变换的表达式如下：

为调节高斯时窗的宽度，向高斯标准差中引入调节因子g，新定义的σ（f）如下：

为了获得较好时频分辨率的适应性，本文以改变g值为手段，通过改变相应的g值来变化高斯时间窗的形状，综合式（7）～（8），可得广义S变换表达式：

通过式（9）得出的广义S变换，即可将经VMD分解后的煤矿井下供电线路的故障行波更进一步细化分解成特定频率的分量，并通过计算得出S模矩阵，继而能进一步采用为Teager能量算子法标定波头。

3.2 基于Teager能量算子的波头标定

由上述VMD－GST处理后的供电线路故障行波，还需通过Teager能量算子法对故障行波的波头进行相应的检测。下式为VMD－GST处理后所获得单频率信号：

式中：ωc为载波频率；q（t）为频率调制偏差；ωm为最大频率偏差；φ（t）为时变相位；θ为初始相位；a（t）为时变幅值。

其中瞬时频率可表示为：

因此信号s（t）的Teager能量算子可表示为：

通过Teager能量算子法能处理故障行波的单分量，可有效识别供电线路故障行波的波形突变时刻，根据突变时刻即可相应地标定初始行波波头。

4 仿真分析

在PSCAD／EMTDC中搭建如图7所示的煤矿井下供电系统，其中该系统为单端交流系统，电压等级为6 kV。

图7 煤矿井下供电系统

在煤矿井下供电系统中，设置A相在距送电侧7.5 km处发生接地故障。此时所测得的两侧关于A相的电流如图8所示。

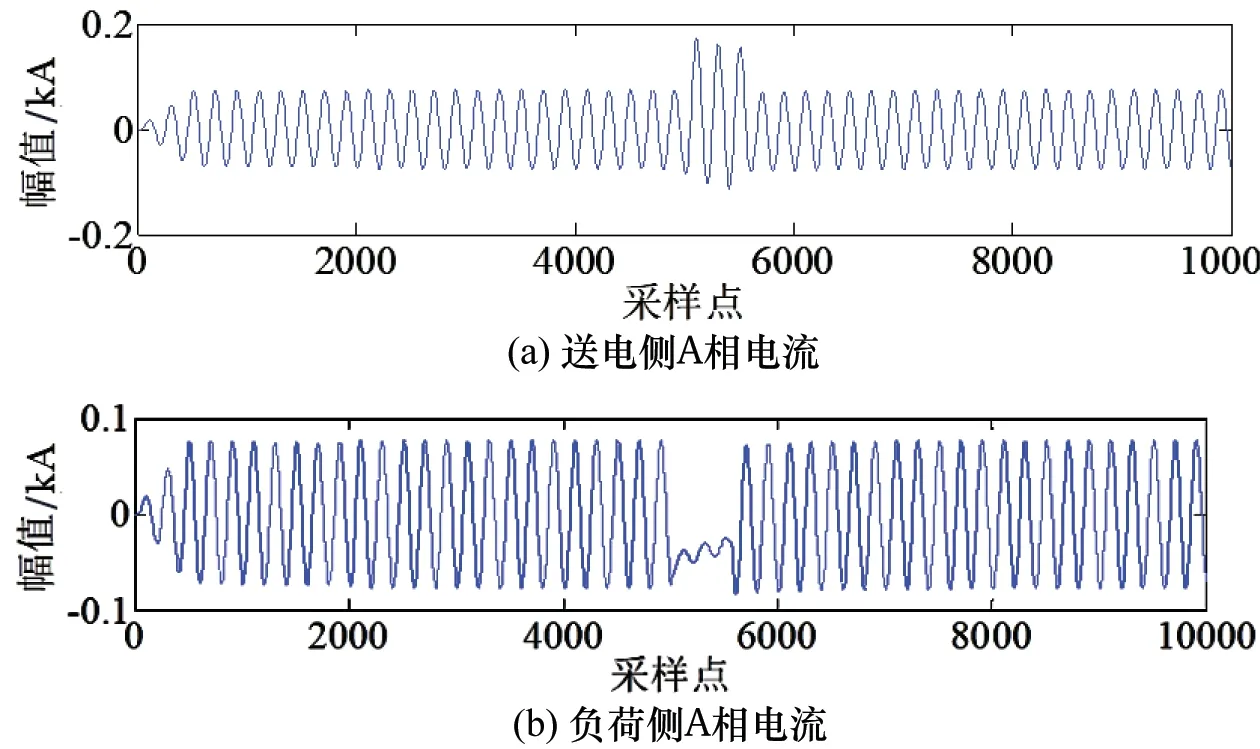
图8 单相短路两侧A相电流

采用VMD算法将图8中的两侧A相故障电流分解，得到两侧的各个模态分量如图9～10所示。由图可知，送电侧和负荷侧的模态分量二的波形的波动情况要远大于其余二种模态分量，且可明显观察到模态分量二含有较为丰富的频率幅值信息。

图9 送电侧电流模态分量

图10 负荷侧线模电流模态分量

因此选择模态分量二作为广义S变换的输入信号，经过相应的变换处理，得到两侧分量的S模矩阵；再通过Teager能量算子法对波形的突变点进行检测，并得到初始行波波头达到两侧的时间，Teager能量算子法处理后的结果如图11所示。由图11综合可知，送电侧和负荷侧行波波头到达两侧的时间点分别为5 025和5 017，且因采样频率为1 MHz，行波波速为v＝2.98×105km／s。将上述参数代入行波测距公式，得出的结果如下：

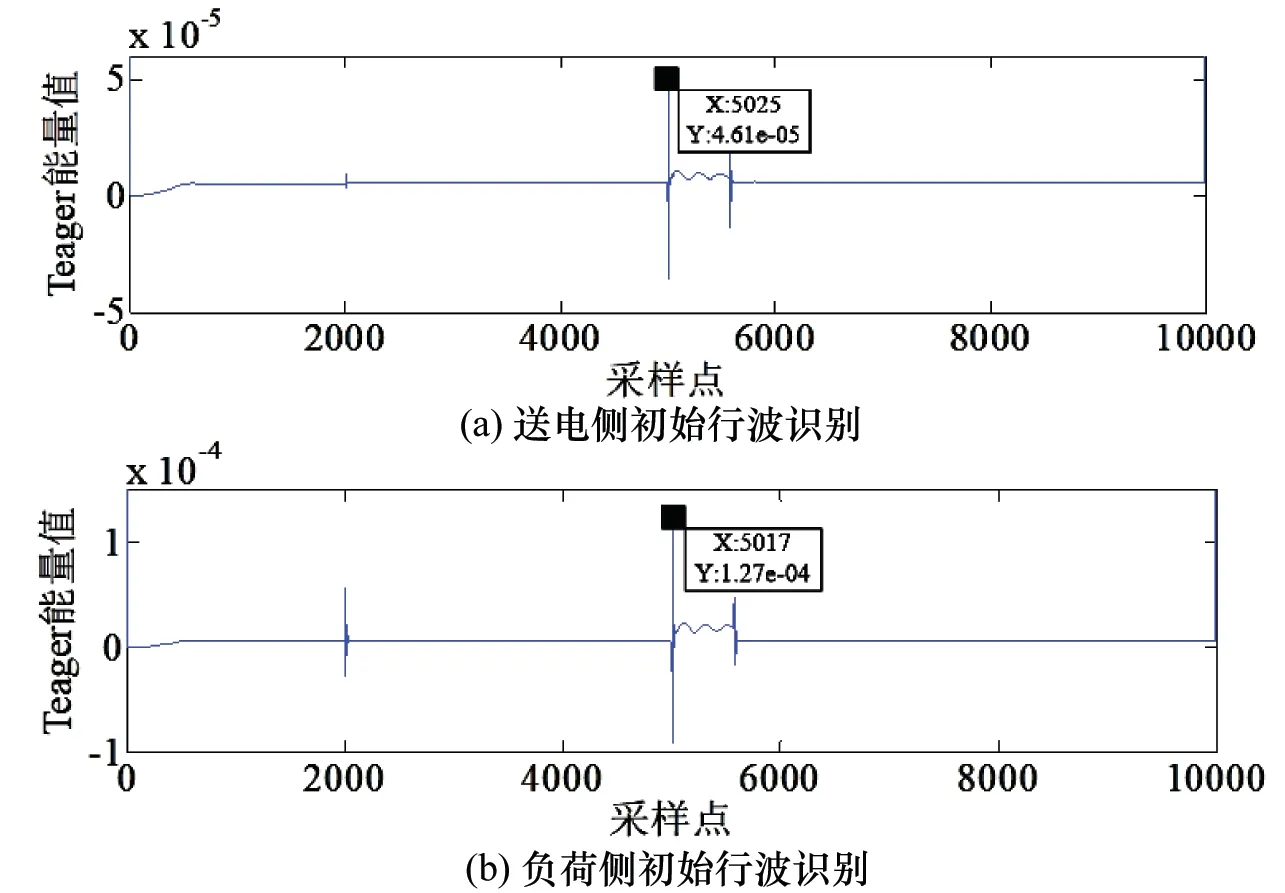
图11 两侧行波识别

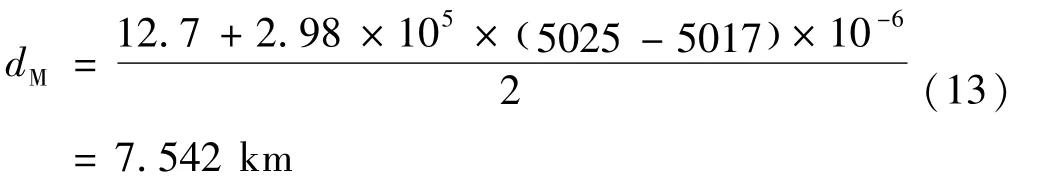
故障点距离送电侧的计算距离为7.542 km，实际为7.5 km，误差为0.542 km，相对误差率为4.3%，因此该故障测距方法于单相接地而言具有较高的测距精度。

5 结束语

本文以煤矿供电系统为例，针对线路故障后的定位精度差问题，提出了基于VMD－GST－TEO的煤矿井下输电线路故障定位方法。首先针对煤矿供电线路的行波传输特征，由此特征将分布参数模型转换成无损均匀模型来分析处理；再通过VMD算法将初始故障信号进行3层分解，得出波动最大的IMF为处理信号，再将其通过广义S变换进一步分解出固定频率的分量；最后再经由Teager能量算子对初始行波波头标定。

通过对PSCAD／EMTDC平台搭建的井下6 kV交流模型中的A相接地故障仿真模拟实验，得出基于VMD－GST－TEO的煤矿井下供电线路故障定位有较高的可靠性。