基于LCC的谐振式无线电能传输负载无关性研究
万祖岩,陈 星,张永超
(大连理工大学机械工程学院,辽宁大连 116024)
0 引言
旋转部件在线监测系统中,为了监测旋转物体的运行状态,便于分析、设计、控制、诊断,需要在旋转部件上安装传感器、信号调理电路、处理器以及无线数据发射电路[1]。这些电路均需要电能,给这些电路的供电方式主要有电池、接触式导电滑环电能传输、非接触式电能传输等供电方式[2]。采用电池方式进行供电时,需要定期充电或更换电池,无法保证系统长期有效在线。采用导电滑环供电时,由于旋转物体本身的运动,会产生导线摩擦、发热等问题,很难保证在旋转部件上长时间使用[3]。而无线电能传输技术(Wireless Power Transmission,WPT)可以避免这些问题的出现,具有无摩擦、使用寿命长、性能可靠等优点,是旋转部件长期在线监测系统需要解决的关键问题之一[4-5]。
本文主要应用感应耦合电能传输技术为旋转部件的在线监测系统进行无线供电,探究此技术能否对负载进行稳压输出。目前有相关文献对无线供电系统的稳压输出进行过研究,但大多数是采用控制电路对其进行闭环控制[6-7],本文主要通过采用设计参数的方法使电路给负载的输出电压具有较好的负载无关性。
本文采用较为常用的LCC型补偿电路,对其基本原理进行探究,计算得出系统负载值以及各线圈通过电流的计算公式和系统输出电压的计算公式,通过公式得出系统谐振频率、电感等各部分电路参数,分析出负载变化对系统稳压输出的影响。基于电路参数,对电路进行仿真和实验,验证分析结果的正确性。
1 电路构成
在ICPT系统中,通常采用增加谐振补偿网络的方式补偿系统中的无功功率,提高ICPT系统的有功功率传输能力[8]。在众多复合谐振拓扑结构中,比较典型的有两种结构——LCL型和LCC型。LCC型谐振补偿先将一个电感L和一个电容C串联,再和另一个电感C并联,既能隔阻直流分量,又能减少滤波电容中的电流脉动,增大发射线圈电流以提升ICPT系统传输距离。
LCC型ICPT电路的拓扑结构如图1所示。图中S1~S4为MOSFET开关管与直流电源构成电压型逆变电路;D1~D4为反并联二极管;Lp1、Cp1和Cp2一起构成发射线圈侧的补偿谐振网络;Lp2为发射线圈,Ls为接受线圈;Cs为接收线圈侧并联补偿电容;R为系统等效负载电阻,Ip和Io为发射线圈电流和负载电流。

图1 LCC型ICPT系统拓扑结构Fig.1 Topological structurediagramof LCCICPTsystem
2 原理分析
电路工作在谐振状态时,谐振网络对高次谐波有很大的抑制作用。同时,对方波周期信号,n次谐波的幅值为基波幅值的1/n。因此,在对电路进行分析时,可以仅考虑逆变后得到电压的基波分量对电路的作用[9]。根据傅里叶技术,逆变后得到电压u1的基波分量的有效值为:

为了便于分析,将图1系统拓扑结构图逆变电源以及各个电感的内阻等效出图2所示电路。

图2 ICPT系统等效电路图Fig.2 ICPTsystemequivalent circuit diagram
在图2中,RLp1、RLp2和RLs分别为补偿电感内阻、发射线圈内阻和接收线圈内阻。则接收侧总阻抗Zs为
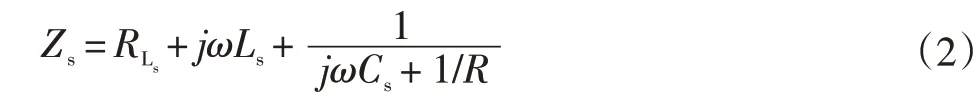
在谐振状态下,接收侧总阻抗在发射端的反映阻抗Zr为[10]:

则将系统接收侧等效发射侧的等效电路模型如图3(a)所示,根据诺顿定理进一步等效为图3(b)所示。
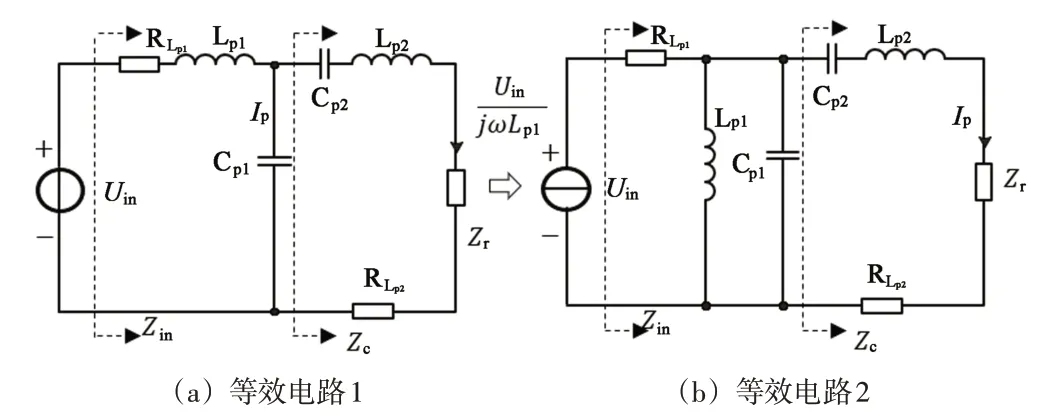
图3 发射端等效电路Fig.3 Transmitter equivalent circuit
在谐振状态下,图3(a)中阻抗Zc为:

在ICPT系统中,由于发射线圈和接受线圈品质因数较高,故可以忽略其内阻,并且在谐振状态下,Ls和Cs相当于开路,故接收侧总阻抗Zs为:

由式(8)和(11)可知,发射线圈的电流仅与输入的电压有关,即当系统负载变化时,发射侧线圈可保持恒定的电流,有利于形成稳定的磁场。由式(12)可得,系统输出电压具有负载无关性,易于实现恒压控制。
3 电路设计
根据式(8)利用Matlab计算得输出电压Uo在不同谐振频率下随负载改变的变化曲线如图4所示。由图可知,系统的输出电压在谐振频率为85 kHz时具有较好的负载无关性,不随负载的变化发生较大改变。

图4 输出电压U o在不同谐振频率下随负载变化曲线Fig.4 The curve diagram of the outputvoltage U o changing with the load under different resonance frequencies
根据实际工况,旋转部件在线监测系统所需输出功率为P0=10 W,设定直流输入电压Vin=15 V,旋转部件各元器件要求输出电压Vout>5 V,增加一定裕量确定Vout=15 V。并确定变压器匝数比以及各个元器件参数。
根据系统的输入以及输出需求,计算得出变压器匝数比N=1。根据公式计算得出变压器发射侧电感为117μH。根据公式Cs(min)=Iin/(8f·ΔUout)可得,输出的电压纹波ΔUout=0.05 V时,Cs(min)=1.02μF,取Cs=1.35μF 。由式(6)计算可得,接收侧电感Ls=102μH;发射补偿电感Lp1=102μH;发射侧补偿电容Cp1=1.35μF,Cp2=1.18μF。互感M=91μH。得出LCC型谐振网络仿真电路参数如表1所示。
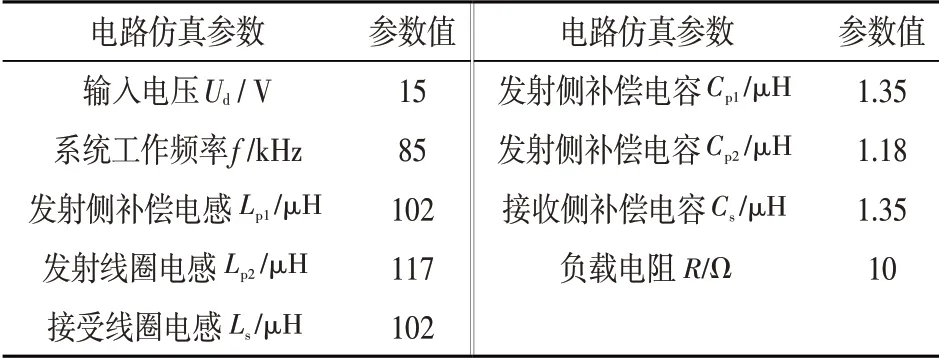
表1 系统电路仿真参数Tab.1 Simulation parametersof systemcircuit
4 仿真分析
基于以上分析过程,使用Simulink对本文电路进行仿真,仿真参数如表1所示,电路系统整体仿真图如图5所示。

图5 LCC型电路系统整体仿真图Fig.5 Overall simulation diagram of LCCtype circuit system
在图5中,给定输入电压为Ud=15 V,输出交流电频率为85 kHz,在t=0.3 s处断开开关使负载10Ω突变到20Ω,图6所示为仿真得出的发射线圈电流Ip的波形。

图6 LCC型负载电阻由10Ω突变到20Ω发射线圈电流波形Fig.6 Thetransmitcoil current waveform of LCCtype load resistance changes from10Ωto 20Ω
为了进一步验证LCC型补偿电路的有效性,将串-并联补偿电路进行对比仿真分析。给定输入电压为Ud=15V,输出交流电频率为85 kHz,在t=0.3 s处断开开关使负载10Ω突变到20Ω,图7所示为仿真得出的发射线圈电流Ip的波形。由图6可得,LCC型补偿电路中原边发射线圈电流不随负载的改变发生变化;而由图7可知,普通的串-并联型补偿电路发射线圈电流稳态赋值在负载电阻突然变化的时候发生较为明显的改变。通过对比仿真分析可知,在两线圈距离固定,线圈间耦合系数一定,电源的输出频率固定时,当负载电阻发生变化时,LCC型补偿网络系统中流发射线圈电流基本保持不变,有利于形成稳定的磁场。
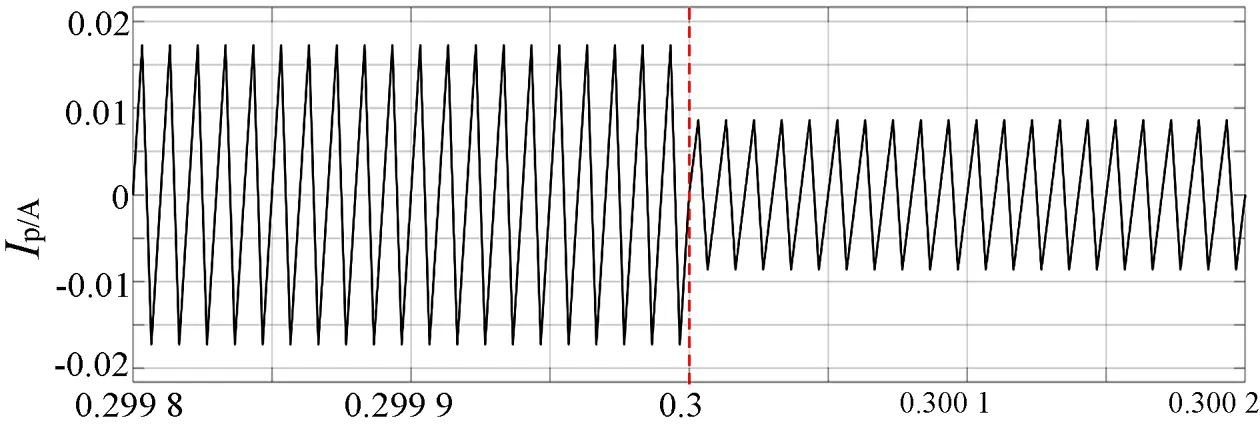
图7 串-并联型电阻由10Ω突变到20Ω发射线圈电流波形Fig.7 The transmitcoil current waveform of series-parallel resistance changes from10Ωto20Ω
5 实验分析
为验证上述分析,根据表1中所示参数以及图5的仿真模型搭建实验平台。实验中给定输入电压为Ud=15V,输出交流电频率为85 kHz,采用接入串联电阻来实现负载电阻的突然增大,观察发射线圈电流Ip的变化情况,实验测试结果如图8~9所示;观察系统整体输出电压的变化情况,如图10所示。

图8 LCC型负载电阻由10Ω突变到20Ω发射线圈电流波形Figure.8 The transmitcoil current waveformof LCCtype load resistancechangesfrom10Ωto20Ω
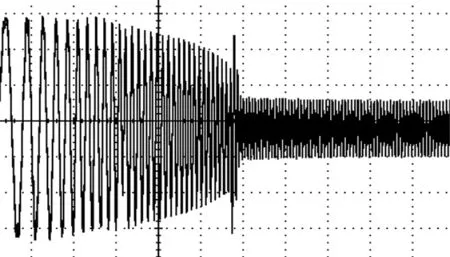
图9 串-并联型电阻由10Ω突变到20Ω发射线圈电流波形Fig.9 The transmitcoil current waveform of series-parallel resistance changes from10Ωto20Ω
测试上述实验波形的仪器为ETA公司的ETA-5301A电流探头和Micsig公司的tBook-mini示波器。由图8、9和图10可知,实验结果证实了仿真结果的正确性。该结果表明在LCC型谐振补偿电路中,当负载改变时,发射线圈电流不随之变化,能够在电路原边形成稳定的磁场,有利于电路稳定运行。同时,该电路也可以保证整个系统的输出电压无明显变化,具有较好的负载无关性,验证了上述理论分析的正确性。
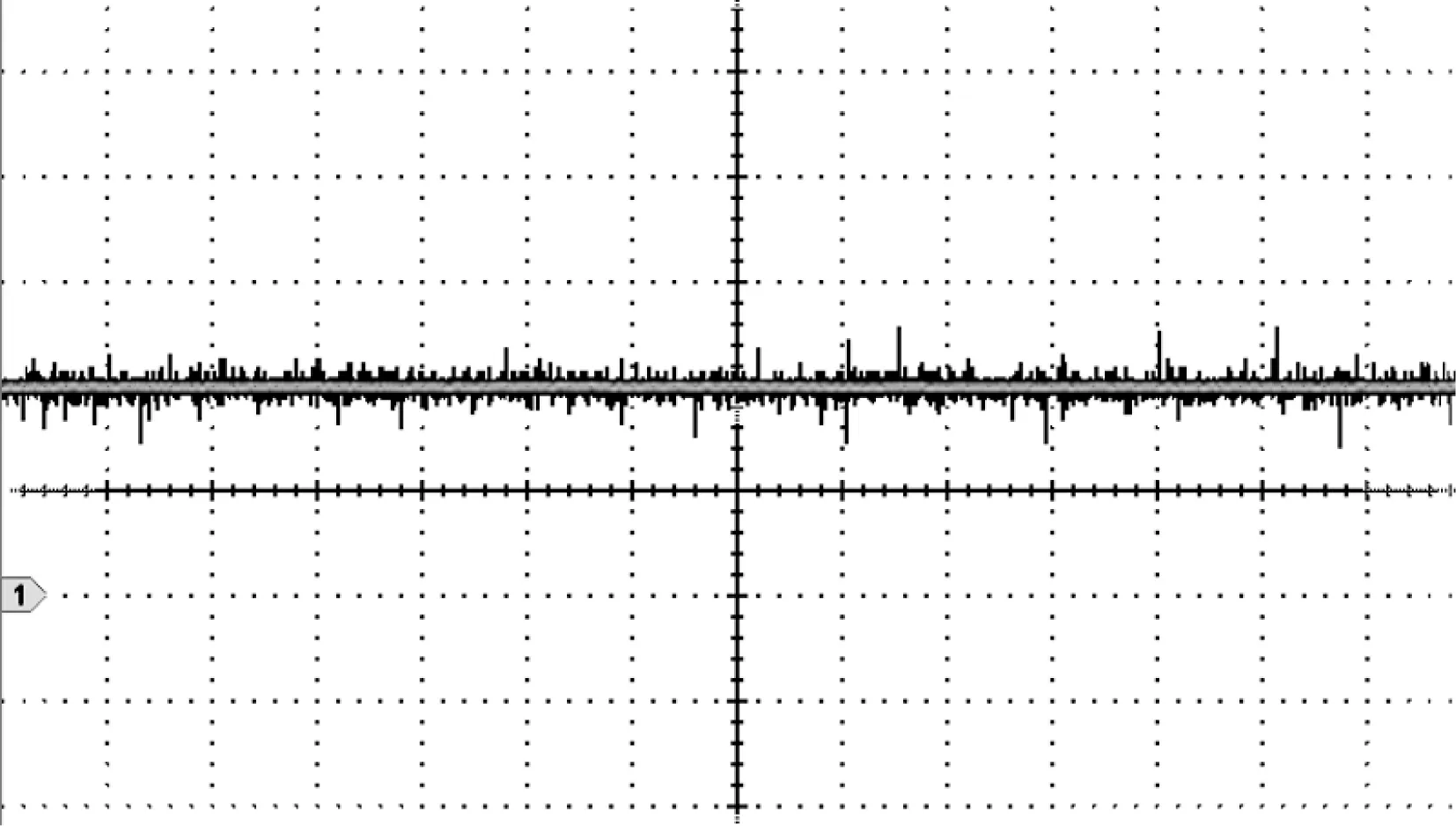
图10 负载变化时输出电压波形Figure.10 Output voltagewaveformwhen theload changes
6 结束语
本文以LCC型谐振补偿网络的ICPT电路模型为研究对象,通过分析其互感模型,得出电路中输出电流表达式,并通过仿真分析,得出了系统工作频率对负载无关性的影响,找出最适合系统的工作频率,并以此工作频率为基础,提出一套ICPT电路系统的参数配置方案与传统串-并联补偿的ICPT电路进行对比仿真分析和实验研究。分析和实验结果表明,在额定条件下,在负载发生突变时,发射线圈电流不会发生突变,有利于电路稳定;系统输出电压基本保持不变。由此可验证本文参数配置下的LCC型谐振补偿网络的ICPT电路系统具有较好的负载无关性。

