天体运动教学中应该重视的拉格朗日点*

吕俊君

(九江市同文中学 江西 九江 332000)

近年我国成功发射了人类历史上第一颗地月中继卫星，并赋予其极具中华传统文化特色的名字“鹊桥”.后续，“鹊桥”将进入环绕地月拉格朗日L2点的使命轨道，完成嫦娥四号与地球之间中继通讯的任务.一时之间拉格朗日点成为学术界热烈讨论的话题，在中学的天体运动教学中，也出现了大量以拉格朗日点为背景素材的试题.那么拉格朗日点具备怎么样的特征，“鹊桥”为什么能够绕L2点做匀速圆周运动，教学中应该如何处理这类问题呢？

1 平面圆形限制性三体问题

如图1所示为一孤立的双星系统，设两星体质量分别为M和m,星体间距离为R，双星靠着相互的万有引力围绕系统的质心做匀速圆周运动.质心O到星球M距离为x1，到星球m距离为x2，则有

图1 双星系统

如果在该双星系统中，放入第3个质量为m0的小物体，小物体不影响M与m的受力情况与运动状态，但小物体同时受到M与m的万有引力作用并能够与他们保持相对静止，以共同的角速度绕质心做匀速圆周运动，小物体应该放在什么位置？这就是“平面圆形限制性三体问题”，该问题有5个特解.1767年数学家欧拉根据旋转的二体引力场推算出其中的3个点(特解)L1，L2，L3，1772年数学家拉格朗日推算出另外两个点(特解)L4和L5；但后来习惯上将这5个点都称为“拉格朗日点”[1].如图2所示，L1点、L2点与L3点均在两星体的连线上，L4点与L5点则分别与两星体构成等边三角形.下面对这5个点进行讨论.

图2 拉格朗日点

1.1 拉格朗日L1点的位置

设拉格朗日L1点处放置一质量为m0的小物体可以在M与m共同的引力作用下绕O点做匀速圆周运动，并和M，m保持相对静止.

设L1点到星体m的距离为x，令x=kR，对物体m0分析，由牛顿运动定律可得

(1)

对m分析，由牛顿运动定律可得

(2)

其中

(3)

由式(1)～(3)联立解得

(4)

可以看出，式(4)即为拉格朗日L1点的通解方程，只要知道M与m的质量之比，就可以求出k值，下面以日地系统为例计算.

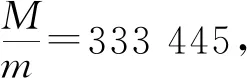
y=(1-k3)(1-k)2-333 445[k2-k2(1-k)3]

通过赋值方法寻找到y为零时k的数值，利用MICROSOFT OFFICE EXCEL工作表对k赋值，计算出以下结果[2]，如表1所示.

表1 日地系统L1点赋值

当k≈0.009 97时，y≈0.因此拉格朗日L1点距离地球约x=kR=1.49×109m处，即拉格朗日L1点在距离地球约149万公里处.

在地月系统中，地球质量

M=5.965×1024kg

月球质量

m=7.349×1022kg

两者质量之比

地球与月球距离R=3.844×108m，构造函数

y=(1-k3)(1-k)2-81.2[k2-k2(1-k)3]

同样通过赋值法求出k数值，如表2所示.

表2 地月系统L1点赋值

当k≈0.151时，y≈0.因此拉格朗日L1点距离月球约x=kR=5.80×107m处，即拉格朗日L1点在距离月球约5.80万公里处.

1.2 拉格朗日L2点的位置

设L2点到星体m的距离为x，令x=kR，对物体m0分析，由牛顿运动定律可得

(5)

对m分析，由牛顿运动定律可得

(6)

其中

(7)

由式(5)～(7)联立解得

在日地系统中，通过赋值法可得k≈0.010 03，因此拉格朗日L2点距离地球约x=kR=1.50×109m处，即拉格朗日L2点在距离地球约150万公里处；在地月系统中，通过赋值法可得k≈0.168，因此拉格朗日L2点距离月球约x=kR=6.46×107m处，即拉格朗日L2点在距离月球约6.46万公里处.

1.3 拉格朗日L3点的位置

设L3点到星体m的距离为x，令x=kR，对物体m0分析，由牛顿运动定律可得

(8)

对m分析，由牛顿运动定律可得

(9)

其中

(10)

由式(8)～(10)联立解得

在日地系统中，通过赋值法可得k≈2.000，因此拉格朗日L3点距离地球约x=kR=2.99×1011m处；在地月系统中，通过赋值法可得k≈1.993，拉格朗日L3点离月球的距离x=7.66×108m.

1.4 拉格朗日L4和L5点的验证

物体m0同时受到M与m的引力作用，设合力方向交M与m的连线于O点，O点距离M的距离设为x，如图3所示.

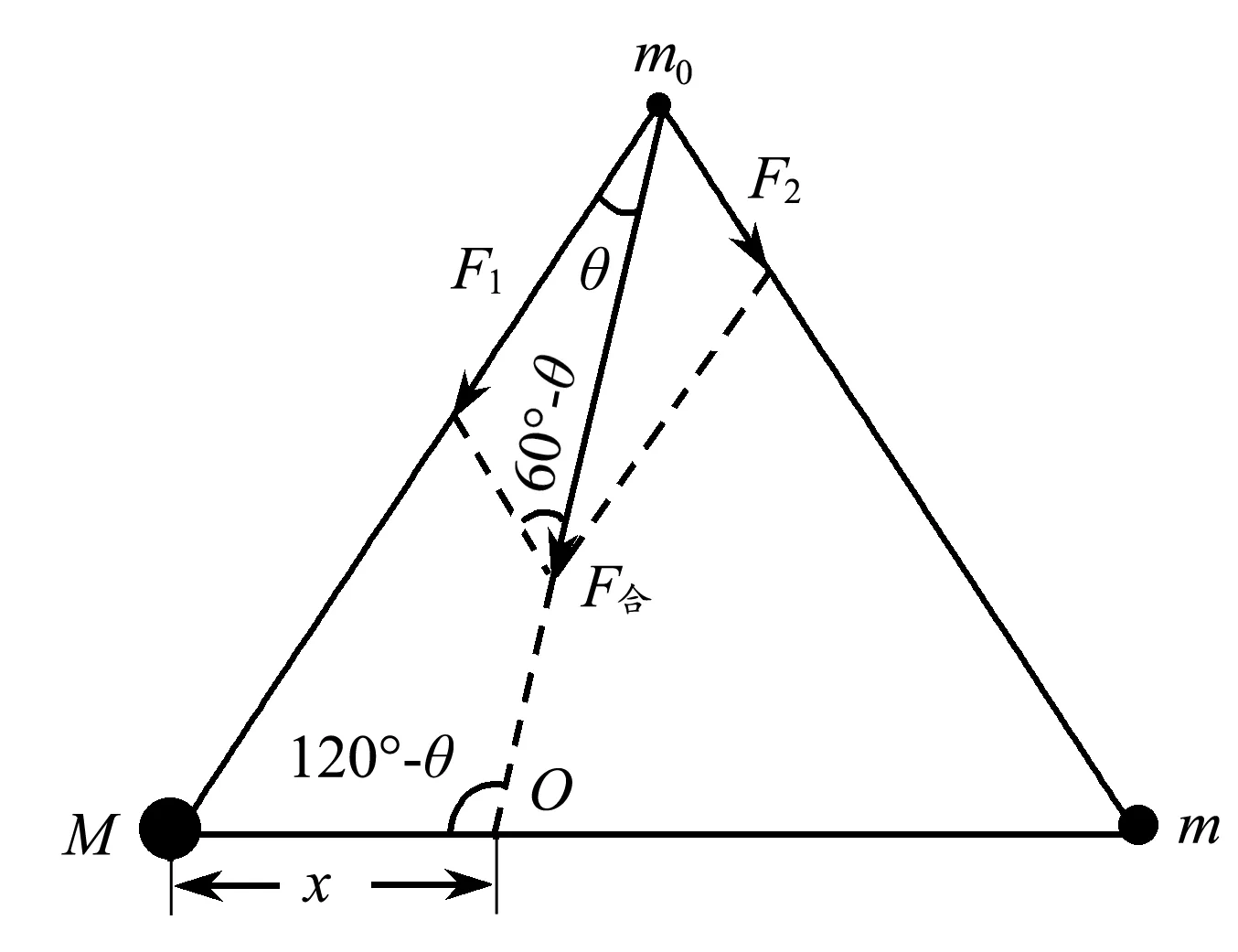
图3 拉格朗日L4和L5点

在力三角形中，由正弦定理可得

通过计算整理,得

(11)

在几何三角形中，由正弦定理得

(12)

将式(11)代入(12)并约去sinθ解出

可以发现，O点的位置就是M与m系统的质心位置，说明，m0将围绕M与m系统的质心做匀速圆周运动，与M和m保持相对静止.

2 “鹊桥”绕地月系统L2点的运动

为了探测月球背面的情况，必须在月球背面放置探测器，然而探测器的信号无法直接传输给地球.为了解决这一问题，需要一颗中继卫星传递信号，构成地球和探测器间的桥梁，这就是“鹊桥中继卫星”(简称“鹊桥”).它的运动可以简化为绕地球公转的同时围绕拉格朗日L2点自转.然而L2点没有任何物体，为何会绕其运行呢？不妨从动力学角度进行分析.

设地球质量为M，月球质量为m，“鹊桥”质量为m0.L2点距离月球为x，地月间距为R.m0的受力情况如图4所示，其中地球对m0的引力大小为

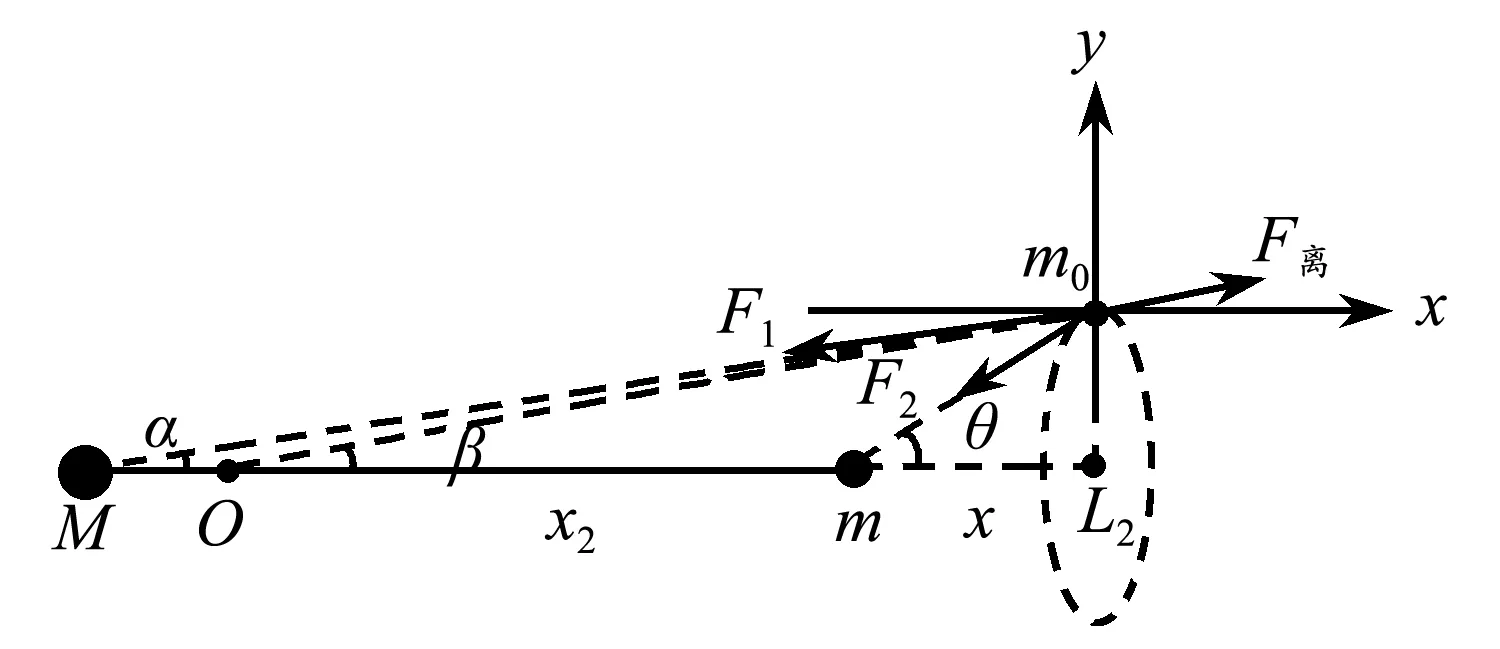
图4 鹊桥在旋转参考系中的受力示意图

月球对m0的引力大小为

按照图中所示建立x,y坐标轴并将各个力正交分解，在x轴方向有

Fx=F离cosβ-F1cosα-F2cosθ=

由于地月系统的质心O离月球很近，且L2点到月球的距离远大于月球的半径，只需要很小的θ角就可以避开月球的阻挡实现中继信号传输[3].可以近似认为cosα≈1，cosθ≈1，可以化简为

由1.2中方程(5)可知Fx=0.

在y轴方向有

Fy=F离sinβ-F1sinα-F2sinθ=m0ω2(x+x2)

由于α与β极小，故tanβ≈0，cosα≈1，cosθ≈1，可得

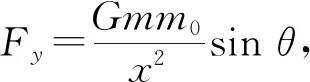
考虑到sinθ≈tanθ，可以求得

这就是“鹊桥”的自转周期大小，可以发现其周期为一定值.

3 天体运动教学中的拉格朗日点

上面的分析均基于系统围绕质心做圆周运动，事实上在日地系统中，由于太阳的质量远远大于地球质量，系统的质心相当靠近太阳.因此在中学阶段，可将太阳看成静止状态，地球绕太阳做匀速圆周运动，地月系统中也是同理.在此基础上，可以归纳出天体运动教学中常见的拉格朗日点模型特征如表3所示.

表3 常见的拉格朗日点模型特征

基于模型特征，中学物理对拉格朗日点通常有如下考查.

3.1 考查拉格朗日L1点

【例1】如图5所示，拉格朗日点L1位于地球和月球的连线上，处在该点的物体在地球和月球引力的共同作用下，可与月球一起以相同的周期绕地球运动.据此，科学家设想在拉格朗日点L1建立空间站，使其与月球同周期绕地球运动.以a1,a2分别表示该空间站和月球向心加速度的大小，a3表示地球同步卫星向心加速度的大小.则以下判断正确的是( )

图5 例1题图

A.a2>a3>a1B.a2>a1>a3

C.a3>a1>a2D.a3>a2>a1

解析：由于空间站和月球的角速度相同，月球轨道半径大于空间站轨道半径，根据a=ω2r可知，a2>a1.同步卫星的周期为1天，月球周期约27天，而且两者均只受到地球的吸引力，说明同步卫星的轨道半径小于月球.

3.2 考查拉格朗日L2点

【例2】如图6所示，地月拉格朗日L2点在地球与月球的连线上，若卫星在L2点，受到地球与月球两大天体的引力作用，能与月球保持相对静止.已知地球质量和地月距离，若要计算L2点与地球的距离，只需要知道的物理量是( )

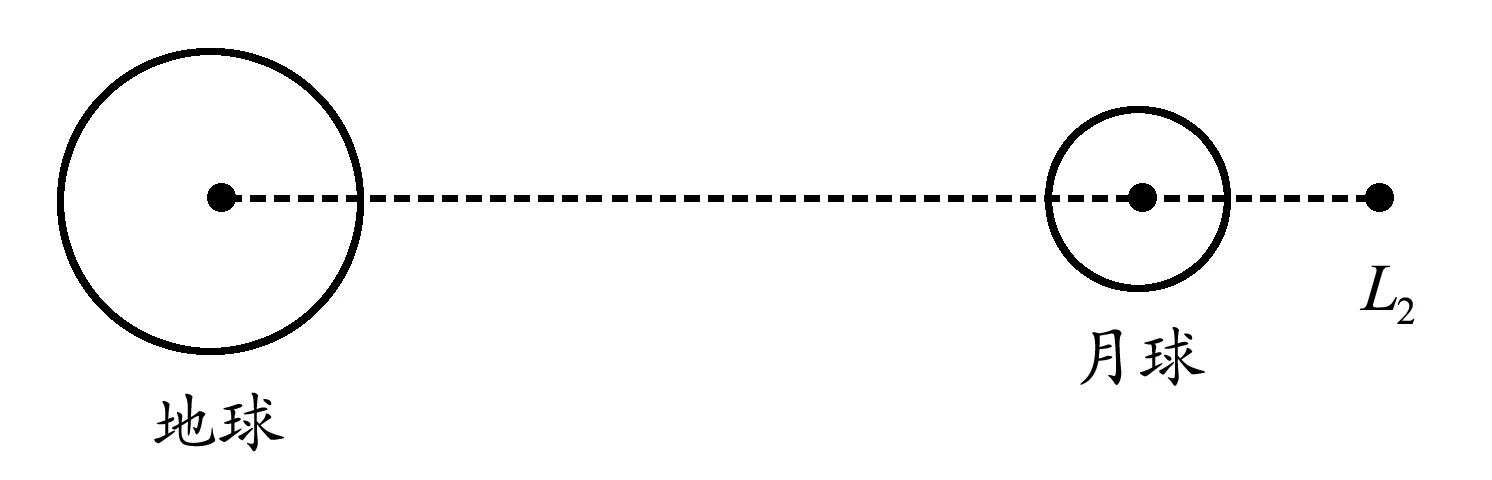
图6 例2题图

A.月球的质量 B.卫星的质量

C.月球绕地球的运行周期 D.引力常量

解析：设地球质量为M，月球质量为m，卫星质量为m0，月地距离为R，拉格朗日点到地球距离为x，其中只有M与R为已知量.

卫星以角速度ω绕地球运动，卫星同时受到太阳与地球的引力.据万有引力定律和牛顿定律，得

(13)

月球绕地球运动的角速度也为ω，根据万有引力定律和牛顿定律，有

(14)

由式(13)与式(14)联立解得

(15)

由式(15)可知，在M与R已知的情况下，只需知道月球质量m，即可求出x，正确答案为A.

点评：本题对卫星和地球分别列出动力学方程，学生需要去思考，为了求出x，需要知道哪些物理量，考查了逆向思维能力.

3.3 考查拉格朗日L4与L5点

【例3】两个靠得很近的天体绕着它们连线上的一点(质心)做匀速圆周运动，构成稳定的双星系统.双星系统运动时，其轨道平面上存在着一些特殊的点，在这些点处，质量极小的物体(如人造卫星)可以相对两星体保持静止，这样的点被称为“拉格朗日点”.现将地-月系统看作双星系统，如图7所示，O1为地球球心，O2为月球球心，它们绕着O1O2连线上的O点以角速度ω做圆周运动.P点到O1与O2距离相等且等于O1O2间距离，该点处小物体受地球引力FE和月球引力FM的合力F，方向恰好指向O，提供向心力，可使小物体也绕O点以角速度ω做圆周运动.因此，P点是一个拉格朗日点.现沿O1O2连线方向为x轴，过O1与O1O2垂直方向为y轴建立直角坐标系；A,B,C分别为P关于x轴、y轴和原点O1的对称点.D为x轴负半轴上一点，到O1的距离小于P点到O1的距离.根据以上信息可判断( )

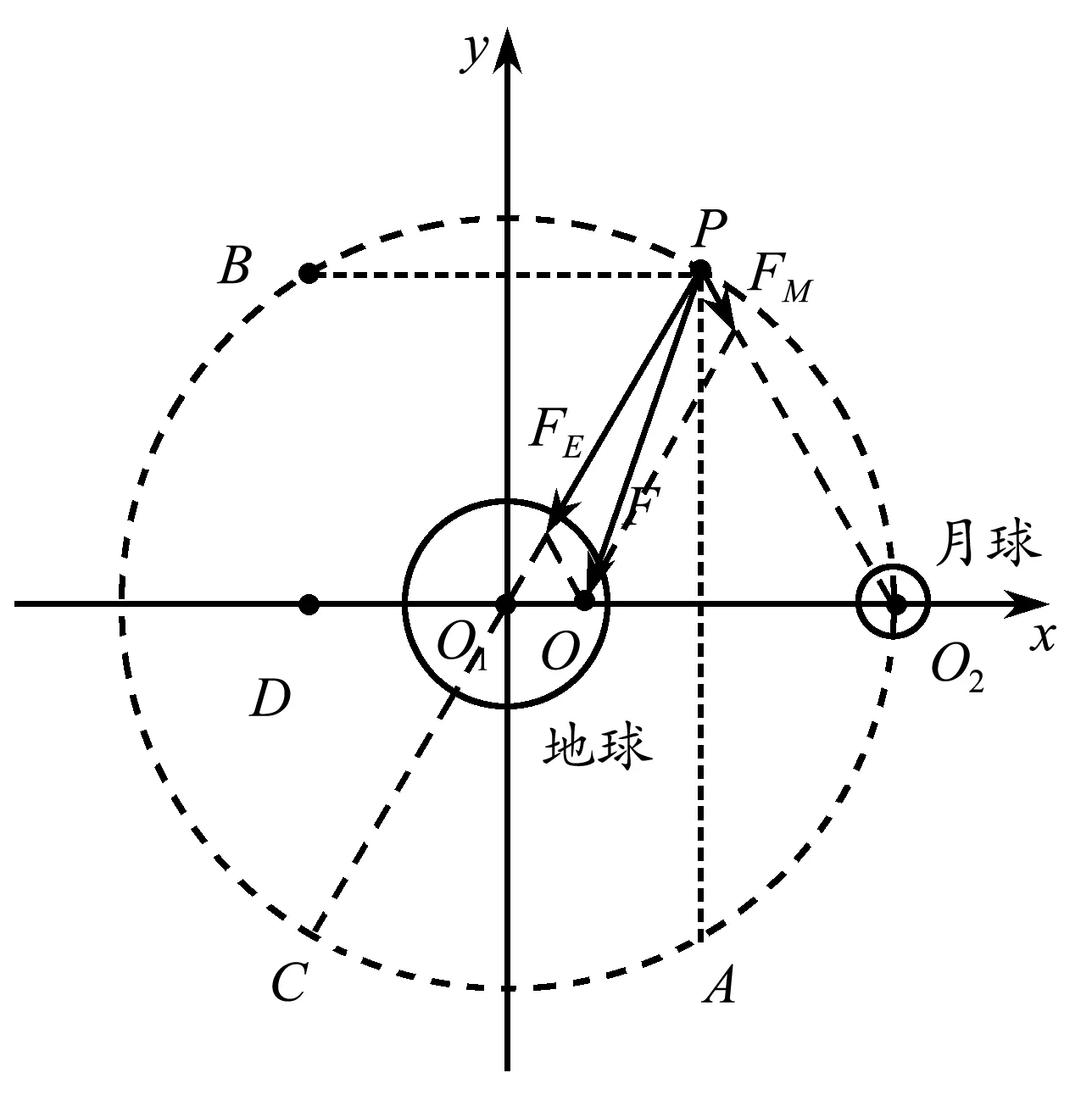
图7 例3题图

A.A点一定是拉格朗日点

B.B点一定是拉格朗日点

C.C点可能是拉格朗日点

D.D点可能是拉格朗日点

解析：根据题中条件可知，P点处小物体受到地球和月球吸引力的合力指向地月系统的质心，和月球以相同的角速度绕地球做匀速圆周运动.根据对称性可知，A点必然是拉格朗日点.B点和P点受到地球的引力大小相等，但受到月球引力比P点处受到月球引力小，其合力方向不可能指向地月系统的质心，考虑到对称性可知，B点与C点均不可能是拉格朗日点.物体如果放在D点，同时受到地球和月球的吸引力，而地球在D点产生的引力加速度大于在月球处产生的引力加速度，说明放在D点处的物体的加速度一定大于月球，因此不能与月球保持相对静止.因此答案为A.

点评：质心是中学阶段不做要求的知识点，本题先介绍了质心的概念并解释了P点是拉格朗日点的原因，要求学生运用所学的知识判断其他点是否为拉格朗日点.学生需要理解新的知识并学会应用它解决新的问题，很好地考查了知识迁移能力.

3.4 鹊桥中继卫星的运动情景

【例4】2019年1月3日，嫦娥四号成功着陆在月球背面开始了对月球背面区域的科学考察之旅.由于月球在绕地球的运行过程中永远以同一面朝向地球，导致地球上的任何基站信号都无法直接穿透月球与嫦娥四号建立联系，为此，我国特意于2018年5月21日成功发射了嫦娥四号中继星“鹊桥”，如图8所示，若忽略除地球和月球外其它天体的影响，运行在地月引力平衡点(地月第二拉格朗日点)的“鹊桥”的运动可简化为同时参与了以L2点为中心的自转和与月球一起绕地球的公转两个运动，以确保嫦娥四号和地球之间始终能够正常地进行通讯联系.以下关于月球和中继星“鹊桥”运动的认识中正确的是( )

图8 例4题图

A.月球的自转周期与其绕地球的公转周期一定是相同的

B.“鹊桥”的公转周期一定大于月球的公转周期

C.“鹊桥”自转的周期一定等于其绕地球公转的周期

D.“鹊桥”绕L2点自转的向心力一定是地球和月球对其万有引力的合力

解析：题干中明确指出，月球在绕地球的运行过程中永远以同一面朝向地球，因此月球的自转周期与其绕地球的公转周期一定是相同的，故A正确；“鹊桥”的公转周期与月球相同，故B错误；题干中没有给出“鹊桥”自转周期的信息，因此“鹊桥”自转周期不一定等于其绕地球公转的周期，故C错误；“鹊桥”同时参与了以L2点为中心的自转和与月球一起绕地球的公转两个运动，“鹊桥”绕L2点自转的向心力由地球和月球对其万有引力、惯性离心力三者的合力，故D错误.因此答案为A.

点评：“鹊桥”同时参与了绕地球的公转与绕L2点的自转，除了学习过物理竞赛的同学，大部分同学都无法转换参考系分析这类问题.但考虑到“鹊桥”同时参与了两个圆周运动，可以定性得到D选项是错误的.A选项也具有隐蔽性，需要学生准确地抓住“月球在绕地球的运行过程中永远以同一面朝向地球”这句话的隐含条件.

4 结束语

研究拉格朗日点可以促进对深空探测技术的突破和掌握，对空间探测的未来发展将起到重要的推动作用[4].我国对该项技术的研究处于世界前列，在教学中渗透相应内容，不仅可以加强学生对天体运动知识的运用，同时有利于树立爱国主义情怀，增强民族自豪感.拉格朗日点在教学中应该重视.