复杂成层土中管桩振动特性分析
王明珠, 杨冬英, 曹雁飞, 陈经伟
(苏州科技大学土木工程学院, 苏州 215011)
学者们针对桩-土振动理论开展了大量研究,在成层土中桩基的振动研究中,王奎华[1]、吴文兵等[2]基于广义Voigt模型,研究了成层土土层参数对桩顶振动特性的影响。何伟杰等[3]研究了大直径桩在成层单相介质土中的纵向振动特性。刘林超等[4]、杨骁等[5]基于饱和多孔介质理论与Novak等[6-7]薄层法,对成层饱和土中单桩的振动问题进行研究。
管桩是近年来出现的一种新型桩,凭借其优势得到广泛应用,同时它的动力特性也得到重视[8]。但是在初期对于管桩的研究是考虑桩侧土为单相介质土或饱和土,崔春义等[9]基于多圈层平面应变模型对单相介质土中管桩的振动特性进行了研究。应跃龙等[10]引入渗透系数,研究了饱和黏弹性地基土中管桩的纵向振动,并讨论了实心桩与管桩桩顶曲线的差异性。文献[11-13]建立了饱和土与管桩的耦合振动模型,分析了施工效应及水的体积分数的影响。为了接近实际土层,将实心桩桩侧成层土的考虑应用到管桩的研究中。崔周飞[14]视管桩桩侧为成层单相土,分析了软硬土层的影响。汤范杨等[15]视管桩桩侧为成层饱和土,进行了土塞相关问题的研究。但是目前为止成层土中管桩的振动研究相对单一,或者纯粹考虑单相介质,或者考虑完全饱和,对实际由于地下水位变化而使桩侧土单相和饱和情况变化的复杂成层土,尚未有学者对这类土中管桩的动力问题进行研究。
为此,假设桩侧土层根据地下水位面,将地下水位面以上视为单相土,以下视为饱和土,建立单相土和饱和土与管桩的耦合振动模型,探究地下水位面变化和地下水位面一定时管桩壁厚、桩周土的性质对桩顶动力响应的影响。
1 数学模型与基本假定
考虑桩侧土体受在地下水位影响导致土层是单相介质和饱和介质的情况,建立管桩与桩侧土耦合振动模型。为了简化计算,将土体分为两层,视地下水位以上为单相介质土,地下水位以下为饱和土,同时桩端视为黏弹性支承,桩顶受到任意激振力的作用,建立单相-饱和复杂成层土-管桩的数学模型,如图1所示。将管桩沿纵向分段,从底部往上根据土层分层编号,每段桩长与成层土层厚度相同。
基于所建模型作出如下假定:①桩周土(单相土与饱和土)视为黏弹性体,桩端视为黏弹性支承;②桩周土(单相土与饱和土)两个土层间的相互作用忽略不计;③管桩为圆形等截面体,其材料视为黏弹性,相邻桩段符合位移连续条件及力平衡;④管桩与桩周土位移连续且桩-土振动满足小变形。
2 土体的动力响应
2.1 饱和土体的动力响应
根据饱和多孔介质理论[16-17]以及下层土体的动力控制方程为[18-19]

q(t)为桩顶竖向激振力;管桩的长度为H,H=h1+h2;内半径为r1;外半径为r2;单相土层厚度为h1;饱和土层厚度为h2;管桩的 外壁剪切应力为τ图1 数学模型Fig.1 Mathematical model

(1)



(2)

(3)

对微分方程[式(2)]进行求解可得其通解为

(4)
式(4)中:K0(λ1r)、I0(λ1r)分别为零阶的第一类及第二类虚宗量的Bessel函数;C1、D1为待求的复系数,与所研究区域土体的边界条件有关。
不考虑无限远处土体的位移,则D1=0,可得

(5)
任意一点土体的竖向剪切应力τ为
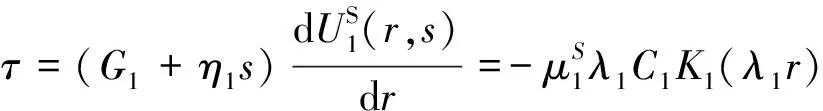
(6)
式(6)中:η1为饱和土体阻尼系数;K1(λ1r)为一阶的第二类虚宗量Bessel函数,由此可得单位长度上饱和土体对管桩的剪切复刚度为

(7)
式(7)中:r2为管桩的外半径。
2.2 单相土体的动力响应
单相土体的振动方程为
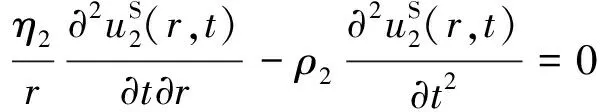
(8)
对式(8)采用Laplace变换并进行整理可得
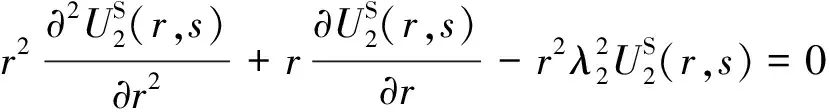
(9)
对式(9)进行求解可得其通解为
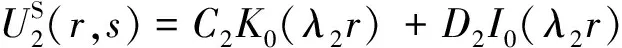
(10)
式(10)中:K0(λ2r)、I0(λ2r)分别为零阶的第一类及第二类虚宗量的Bessel函数;C2、D2为待求的复系数。
不考虑无限远处土体的位移,则D2=0,可得

(11)
任一点土体的竖向剪切应力τ为

(12)
式(12)中:K2(λ2r)为一阶的第二类虚宗量Bessel函数,由此可以得到单位长度上单相介质土体对管桩的剪切复刚度为

(13)
3 管桩的纵向振动方程与求解
任取管桩的微元体进行分析,则管桩的纵向振动方程为
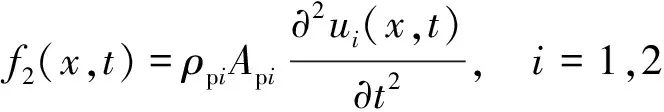
(14)
式(14)中:ui(x,t)为第i段管桩的桩身位移;f1(x,t)、f2(x,t)分别为管桩内侧及外侧的摩擦阻力;r1为管桩的内半径;r2为管桩的外半径;Epi、Api、ρpi、ηpi分别为第i段管桩的杨氏模量、截面面积、桩身密度、桩身材料阻尼。
桩顶边界条件与桩底边界条件分别为
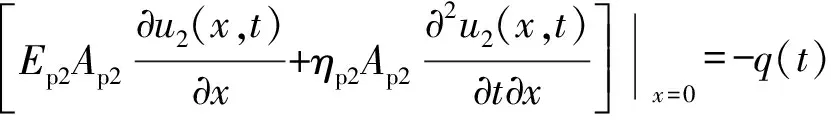
(15)

(16)
式(16)中:kp为弹簧系数;δp为阻尼系数。
应满足的初始条件为

(17)
连续条件为
ui(x,t)|x=hi=ui+1(x,t)|x=hi
(18)

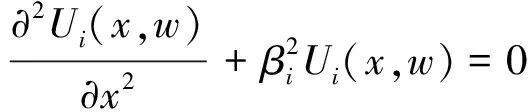
(19)
对式(19)进行求解可得
Ui(x,w)=Micos(βix)+Nisin(βix)
(20)
式(20)中:Mi、Ni为待求常数,可根据边界条件求得。
对桩底的边界条件采用Laplace计算可得
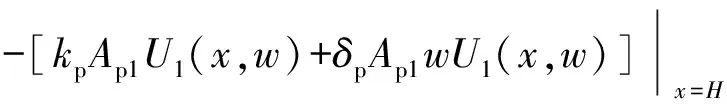
(21)
按照位移阻抗的概念(力与位移的比值)可以得出第1段管桩桩底处的函数表达式为
-[Ap1(kp+δpw)]
(22)
进行整理并无量纲化可得

(23)


(24)
式(24)中:l1为第一段管桩的长度。
按照位移阻抗的概念(力与位移的比值)可以得出第1段管桩桩顶处的函数表达式为
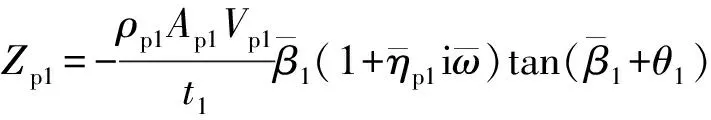
(25)
根据递推关系可以得到桩顶的位移阻抗表达式为

(26)
对式(26)采取无量纲化可得
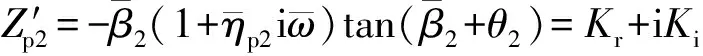
(27)
式(27)中:Kr为无量纲动刚度;Ki为无量纲动阻尼。
桩顶速度导纳Hv的表达式为
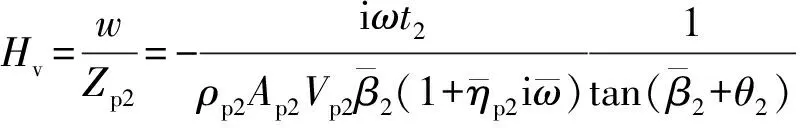
(28)
将式(28)进一步无量纲化得
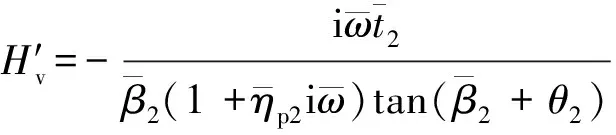
(29)
假设桩顶所受的振动力为

(30)
式(30)中:T0为脉冲宽度。
对q(t)采取Laplace变换可得

(31)
式(31)中:Q为q(t)的Laplace变换。
根据卷积定理得出桩顶时域表达式为
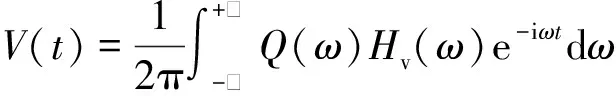
(32)
对式(32)进行无量纲化可得

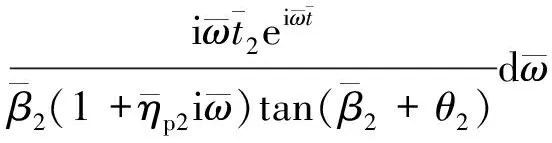
(33)
4 相关参数分析
桩土参数不同往往对桩基础的振动特性产生影响,以下进行两种情况下的相关桩土参数对管桩振动特性的影响研究。第一种是地下水位面变化的影响研究,第二种是地下水位面一定下管桩参数影响研究。
计算时桩土参数取值如下:桩周土体(下层饱和土)的参数:土体密度为2 000 kg/m3,剪切波速Vs1为200 m/s,水的体积分数为0.33;桩周土体(上层单相土)参数:土体密度为1 800 kg/m3,剪切波速Vs2为180 m/s,两土层阻尼比均为0.05;管桩的参数:管桩长度为12 m,内、外半径分别为0.3 m,0.5 m,桩身密度为2 500 kg/m3,纵波波速为4 000 m/s,泊松比0.25,桩身材料阻尼为0。弹簧系数无量纲化取为0.1,阻尼系数无量纲化取为0.06,脉冲宽度为0.8 ms。
4.1 地下水位面影响
桩侧整体土层厚度12 m为定值,地下水位面距桩底的距离为h1,即桩侧饱和土层厚度为h1,另h1取0、3、6、9、12 m。
图2呈现的是地下水位面改变与桩顶速度时域曲线及幅频曲线的关系。
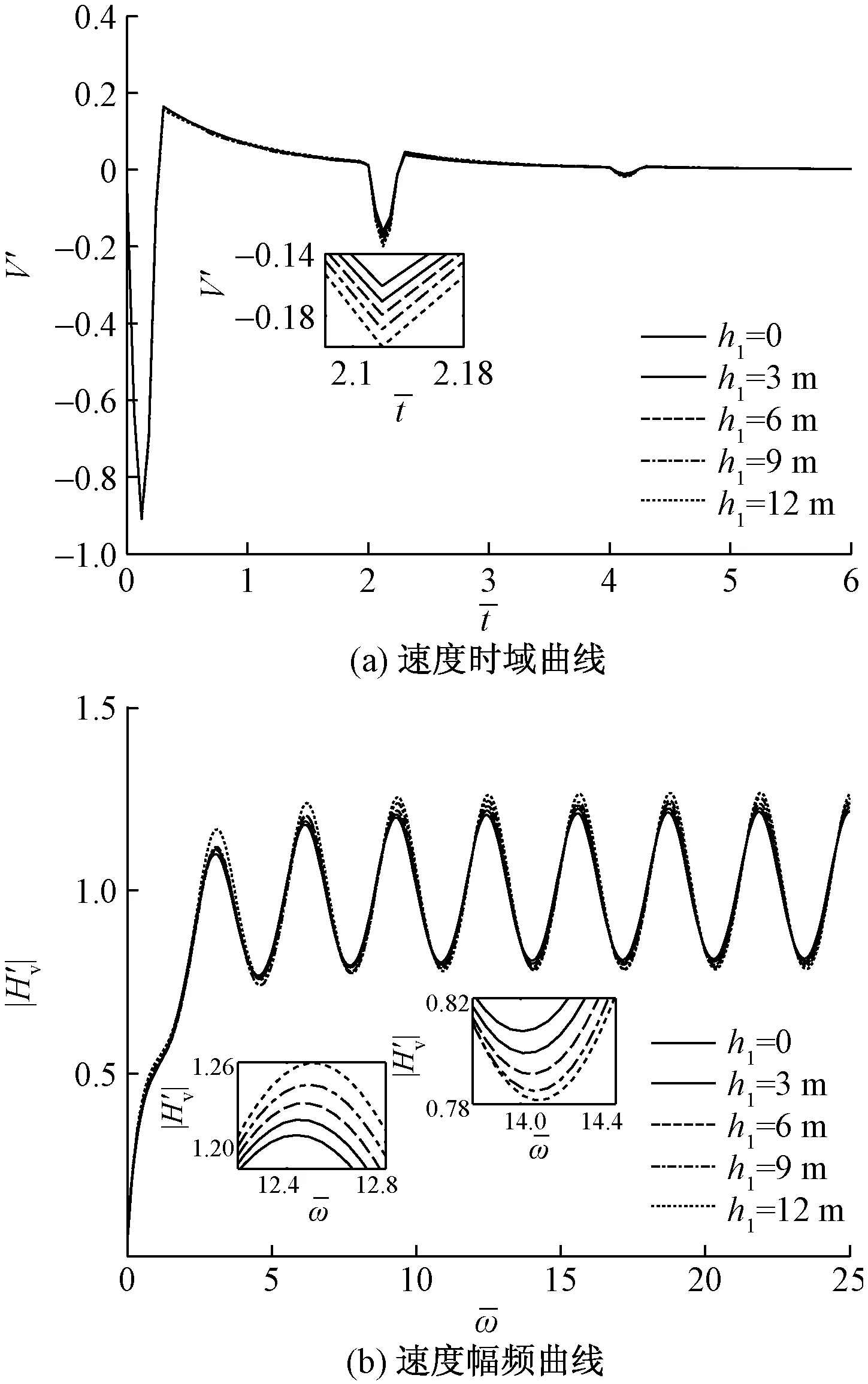
|H′v|为速度导纳H′v的模;为无量纲频率; V′为时域响应无量纲因子;为无量纲时间因子图2 地下水位面对桩顶速度的影响Fig.2 Influence of groundwater level on pile top velocity
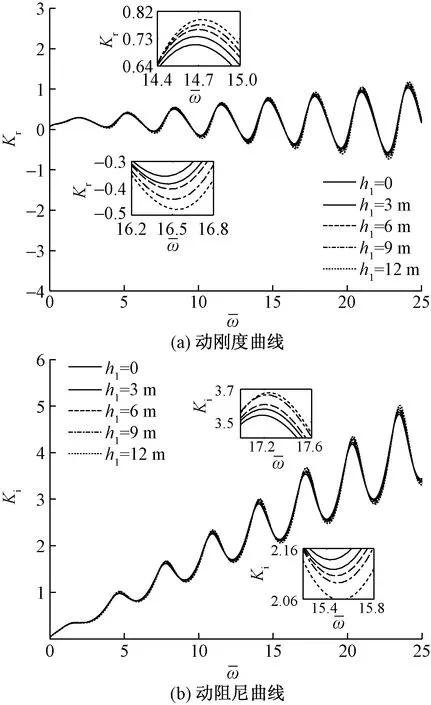
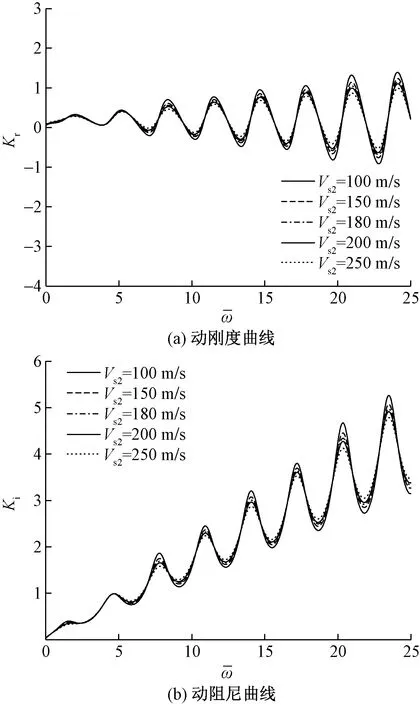
图3 地下水位面对桩顶阻抗的影响Fig.3 Influence of groundwater level on pile top impedance
当地下水位面在桩底时,此时饱和土层厚度为0,也就是桩周土为均质单相土时,时域曲线反射信号幅值相对较小,随着地下水位面的升高,反射信号幅值逐渐增大,这是由于土体的含水量不断增多,土体对管桩的约束力慢慢减弱,吸收能量的能力也降低,形成了曲线幅值越来越大的现象;速度幅频曲线表现出地下水位面越高、饱和土层厚度越大幅值越大的情形,是振动能量吸收降低造成的。
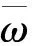
4.2 管桩壁厚改变的影响
地下水位面在距桩底6 m时,分析管桩壁厚改变对桩顶振动特性的影响,所得桩顶速度曲线与阻抗曲线如图4、图5所示,分析过程中管桩外半径为0.5 m保持不变。
图4(a)反映出管桩外半径不变时,壁厚b越大,桩尖同向反射信号越强。由此可见,随着壁厚的不断增大,管桩截面积也变大,纵波传播速度快,消耗的能量少,故反射幅值较为明显;从图4(b)中看出,壁厚为0.1 m时,速度导纳曲线与其他曲线在波动幅度上存在明显的差异,其波动幅度最小,壁厚越大曲线的波动幅度越大。
由图5可以看出,壁厚对桩顶阻抗存在较大的影响,壁厚最小为0.1 m时动刚度、动阻尼曲振荡幅值很小,随着壁厚的增加幅值增大,同时从单一曲线看振动幅值随着无量纲频率的增大逐渐上升增加。
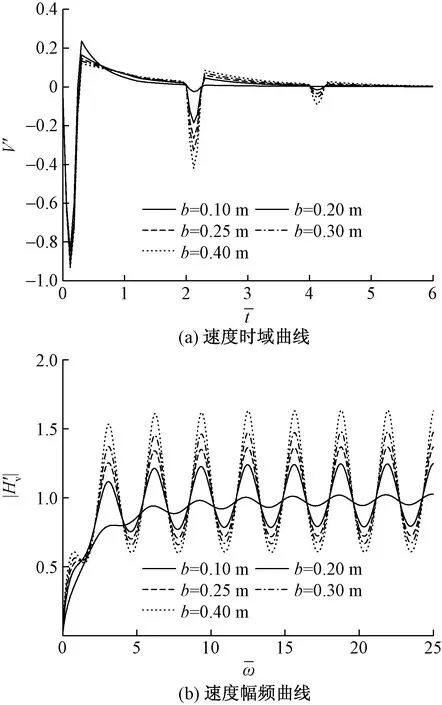
图4 管桩壁厚对桩顶速度的影响Fig.4 Influence of pipe pile wall thickness on pile top velocity

图5 管桩壁厚对桩顶阻抗的影响Fig.5 Influence of pipe pile wall thickness on pile top impedance
4.3 不同桩周土中管桩振动特性的对比
将桩周土分为成层单相土、成层饱和土、单相-饱和复杂成层土,对桩顶的振动情况进行对比分析。其中单相-饱和复杂成层土中地下水位面在距桩底6 m处(饱和土层厚度和单相土层厚度都为6 m)。以单相-饱和复杂成层土为基础,首先,令下层饱和土中水的体积分数为0,其余参数保持不变,使其成为成层单相土;其次,在参数不变的情况下将上层单相土变成饱和土,使其成为成层饱和土。
从图6(a)中可以看出,桩周土的性质对桩顶的振动特性存在一定的影响,桩周土不同时,桩尖反射的幅值存在明显的差异,当桩周为成层单相土时,反射波振幅最小,下层土变为饱和土层时,振幅变大直至桩周土变为成层饱和土时振幅最大。从图6(b)可以看出,不同桩周土作用下产生的幅频曲线上下振荡呈规律性变化,不同之处在于振幅大小,表现出成层饱和土中桩顶的振动幅度最大,成层单相土中桩顶的振动幅度最小的情形。
图7中动刚度、动阻尼曲线都表现出随着共振频率的增大振动幅值逐渐增大的现象,并且三者的波动频率一致。此外,桩周由成层单相土变化到成层饱和土时,由于土体含水量不断增多,纵波传播消耗的能量减少,导致桩周为成层单相土、单相-饱和复杂成层土时桩顶的振幅远小于桩周为成层饱和土时的振幅。
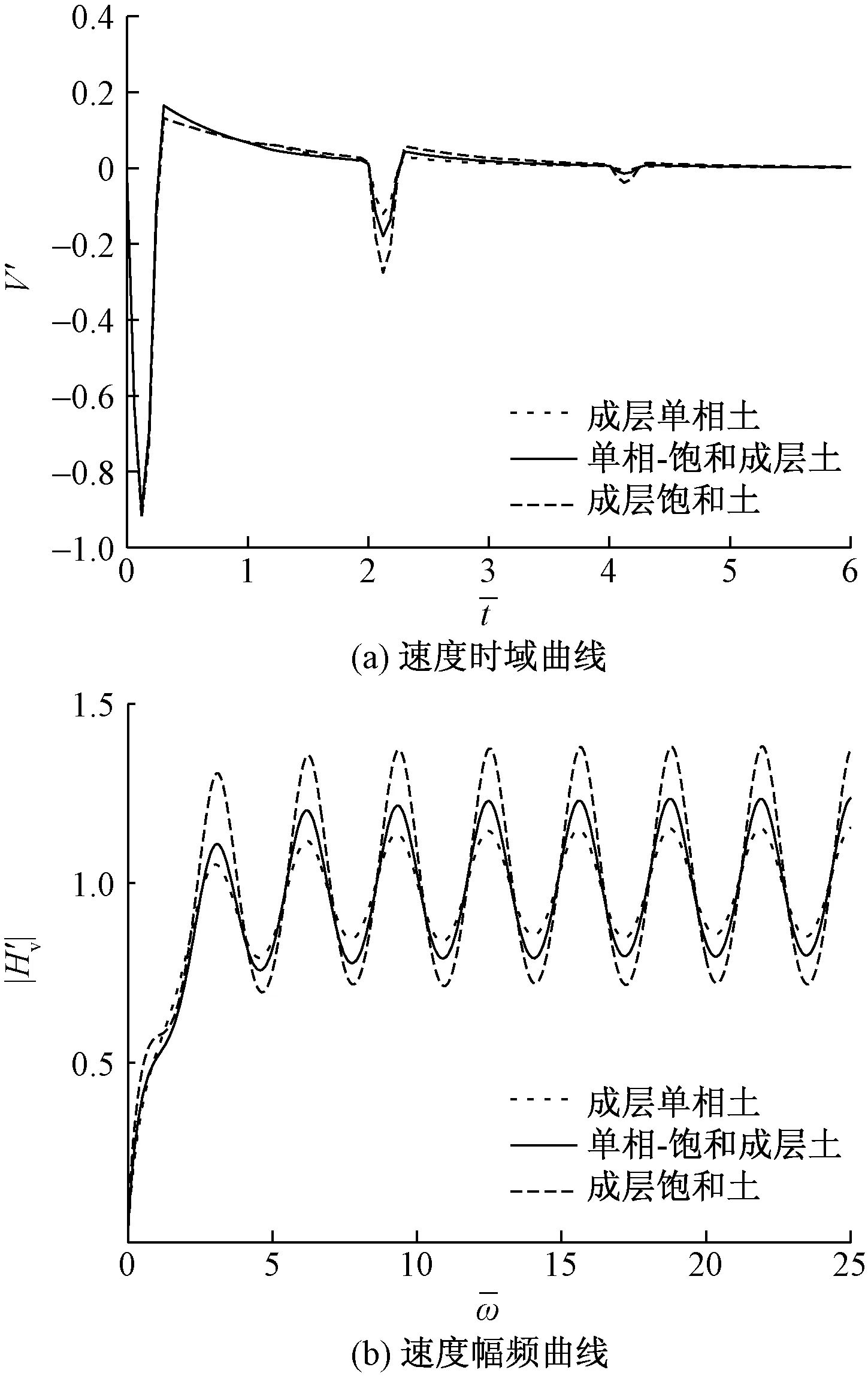
图6 不同桩周土对桩顶速度的影响Fig.6 Influence of different soil around pile on velocity of pile top
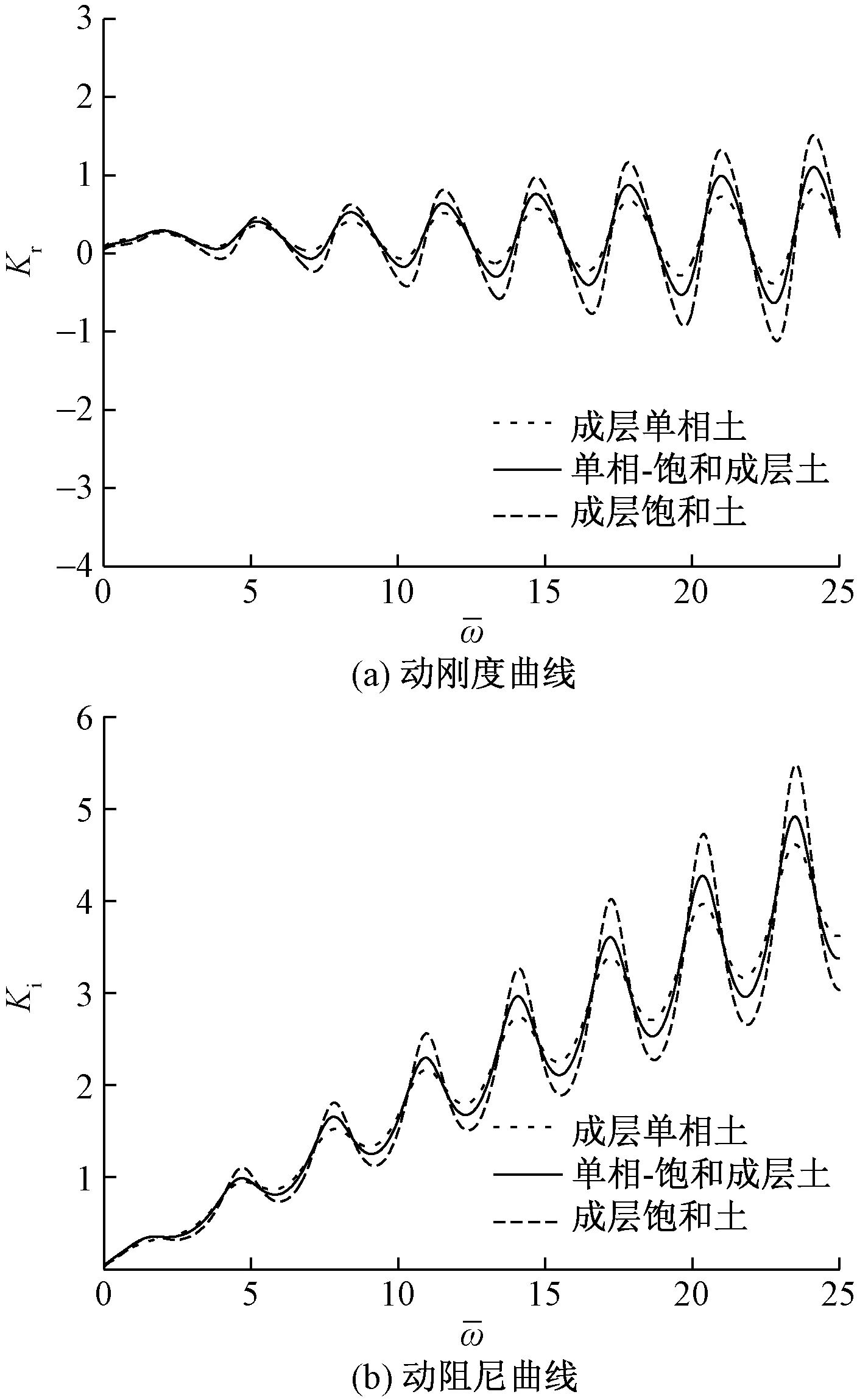
图7 不同桩周土对桩顶阻抗的影响Fig.7 Influence of different soil around pile on impedance of pile top
4.4 软硬土层的影响
以上是考虑桩周为纵向两层的非均质土,为了明确软硬土层对桩顶响应的影响,进一步将桩周土纵向分为三层(饱和土体分为等厚度的两层,单相土层不变),第一层饱和土和第三层单相土的参数同上一致,第二层饱和土通过改变土体剪切波速实现软硬土层变化。Vs1=200 m/s,当Vs1>Vs2时,说明土层为上软下硬;当Vs1=Vs2时,说明土层均质;当Vs1 图8显示桩周软硬土层会对桩顶曲线产生明显的影响。由图8(a)可知,桩顶接收到桩底反射信号之前,首先收到了土层交界处传递的微小信号波,当第一层土的性质优于第二层时,微小信号波为同向反射,当第一层土的性质差于第二层时,微小信号波为反向反射。同时也可得到,土的剪切波速越大,土体的性质越好,传递反射信号会消耗更多的能量,因此反射信号幅值越小。由图8(b)可知,第二层土为软土层时得到幅频曲线的幅值显著大于均质土时的幅值,而第二层为硬土层时,曲线幅值相对于均质土较小。 图9为软硬土层对桩顶阻抗的影响。动刚度曲线和动阻尼曲线随着剪切波速的增大,土体的性质逐渐变好,相反幅值越小。饱和土层存在软硬土层时与均质饱和土的计算结果存在较大差异,由此可见软硬土层这个因素对桩顶阻抗的影响不容忽视。 图8 软硬土层对桩顶速度的影响Fig.8 Influence of soft and hard soil on pile top velocity 图9 软硬土层对桩顶阻抗的影响Fig.9 Influence ofsoft and hard soil on pile top impedance 以地下水位面为界,进行单相-饱和复杂成层土中管桩的纵向振动研究,具体分析了地下水位面变化、管桩壁厚和桩周土参数的影响,得出如下结论。 (1)地下水位面变化对桩顶振动特性有一定的影响,并且地下水位面在桩底位置时,曲线的幅值最小,随着地下水位面逐渐升高,曲线的振荡幅值也越大。 (2)管桩壁厚较小时动刚度、动阻尼曲线趋近于一条直线,随着壁厚的增大,曲线波动幅度增大,幅值增大;成层单相土、单相-饱和复杂成层土、成层饱和土三种桩周土的曲线振动幅度依次增大,且前两者的峰值远小于第三种情况,由此可知管桩壁厚及桩周土体性质的影响不可忽略。 (3)桩周的饱和土层无论是存在软土层还是硬土层,桩顶的速度曲线和阻抗曲线都与均质饱和土层的曲线存在显著差异,由此得到桩周土的复杂成层性能够对管桩桩顶动力特性造成影响,并且影响程度由土体的性质决定。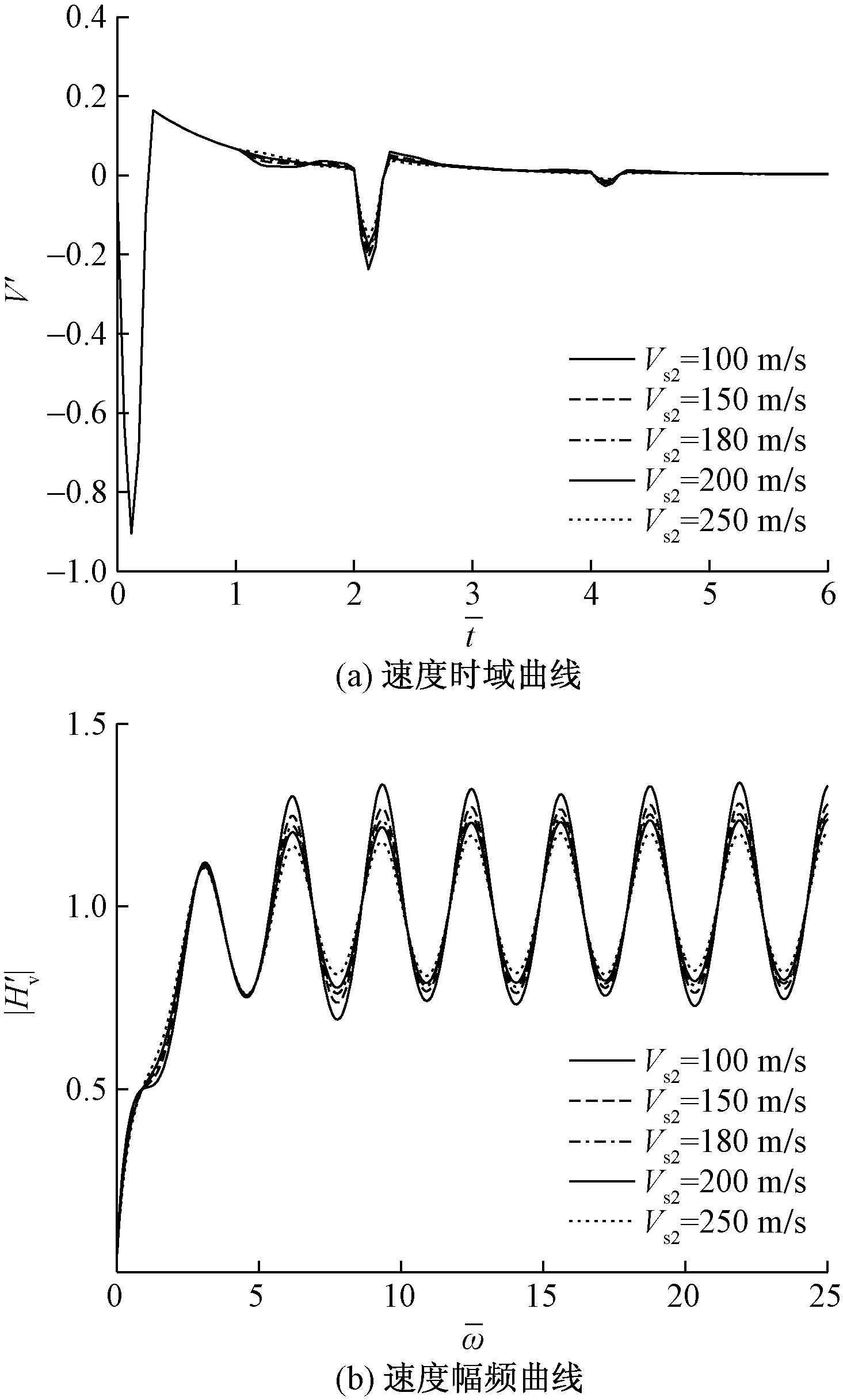
5 结论

