基于模糊免疫PID定型机拉伸张力控制技术

岳跃腾， 赵世海

(天津工业大学机械工程学院， 天津市现代机电装备技术重点实验室， 天津 300387)

定型机是在规定的张力、温度作用下对织物进行工艺加工，使其到达稳定状态的设备[1]。近年来中国相关企业利用国外技术成熟的定型机控制系统进行研制，但因技术水平有限，研制出的定型机控制系统在稳定性、精准度上远落后于同等标准下的国外定型机控制系统[2-3]，并且在织物加工过程中，对织物纵向拉伸的处理是定型的关键步骤，不仅可以使织物到达所需的尺寸，还能改善织物的内部结构，这对织物的拉伸强度和稳定性极其有利，但是拉伸张力的波动会对织物的质量及后续的加工产生影响[4]。如果张力过大，织物会出现破裂，引起织物强度降低发生变形;反之张力过小，织物内应力不易被消除，会使其出现皱褶，产生弯曲，达不到合适的定型尺寸[5]，所以保持拉伸张力控制系统的稳定性及控制精度尤为重要。

由于常规PID(proportion integral differential)操作简单，因此被广泛应用在定型机张力控制系统中。但是其存在很大的不足，实际工业生产中通常是非线性的，并且随时间的推移而变化，且其具有信号提取不准确、达到稳定时间慢等局限性，一旦内外环境发生变化，系统就会受到干扰[6-7]。所以对于拉伸张力控制这类具有强干扰及强耦合的非线性时变系统[8]，采用常规PID控制已不能达到理想控制效果，则需改进控制器，适应当前工艺的需求。近年来，越来越多的控制方法被应用在张力控制中，如谭宝成等[9]将变结构遇限削弱积分PID技术解决定型中张力稳定控制问题；张立冬等[10]利用PI (proportion integral )变频调速来实现恒张力控制，但是以上方法均建立在精确的数学模型基础上，并且在实际生产中会有多种因素不能具体体现在数学模型中，从而会影响这些方法的使用。

因此针对定型机拉伸张力控制的问题，结合生物免疫系统的启发，为实现对定型机拉伸张力系统的调控，从而取得性能优异的织物，设计一种基于模糊控制+免疫算法+PID控制的联合控制系统的技术[11-13]，通过MATLAB模拟仿真和应用测试表明该技术可以解决系统抗干扰能力弱以及动态性能差等问题，能够保证系统稳定运行。

1 张力数学模型的建立

以定型机拉伸张力为对象进行分析，在定型过程中对织物进行纵向拉伸使其张力恒定，目的是让其拥有设定的尺寸及更佳的定型效果。从定型工艺可知，主动辊和拉伸辊之间会产生织物的拉伸张力，而主动辊和拉伸辊会使织物处于绷紧状态，此时纵向张力达到初始张力值，它们之间产生的速度差造成织物伸长变形，从而出现拉伸张力。其中拉伸示意图如图1所示。

图1 定型机拉伸示意图

设m1、m2为织物质量，g1、g2为物质密度(织物单位长度质量)，v1、v2分别为主动辊和拉伸辊所带动织物的速度(即为织物线速度)。可得织物拉伸单位伸长量为

am=am2-am1=(g2v2-g1v1)dt

(1)

式(1)中：a为织物宽度；t为时间变量。

织物单位伸长量所对应的织物单位质量为

am=g2dΔl

(2)

式(2)中：Δl为织物伸长量。

由式(1)和式(2)可得

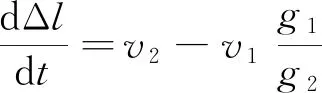
(3)

主动辊和拉伸辊端口织物长度质量满足

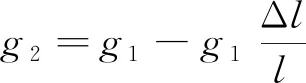
(4)

式(4)中：l为织物长度。

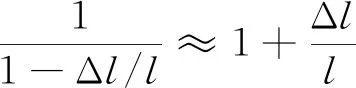
(5)

由式(4)和式(5)可知速度差和伸长量的关系为

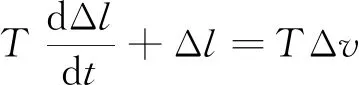
(6)

式(6)中：T为时间常数；Δv速度差。

根据胡克定律可知

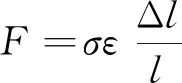
(7)

式(7)中：F为织物张力；σ为横截面积；ε为弹性模量。

由以上各式可知拉伸张力和速度之间满足

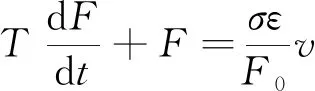
(8)

式(8)即为织物拉伸张力模型，在定型过程中，系统通过张力反馈信号来调整拉伸速度，以此保证张力恒定。

本文设计的定型机张力控制系统如图2所示，采用张力传感器来测试控制对象的张力，人机操作界面用来监控设备及参数的设定，通过A/D转换器将模拟量转换成数字量输入到PLC中，采用模糊免疫PID(proportional integral derivative)算法进行运算，且将控制算法运行出的数据通过D/A转换器转变成模拟量，最后将模拟量通过执行机构输出到被控对象。

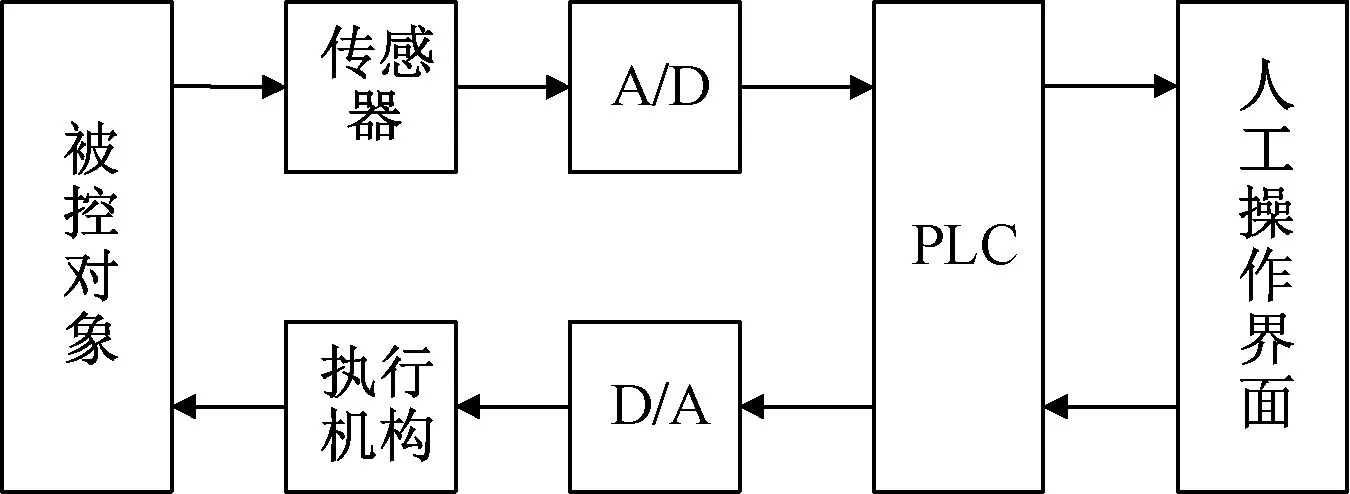
图2 定型机张力控制系统

2 模糊免疫PID控制器的设计

2.1 免疫反馈原理

免疫是指人体自身的免疫系统识别自身相互排斥的物质，即入侵的抗原，并产生对异物具有抗性的抗体，生物免疫系统主要由抗体分子和淋巴细胞组成，而淋巴细胞是由骨髓中的B细胞和胸腺中的T细胞(分为正细胞Th和负细胞Ts)组成[14]。当抗原入侵生物时，它与特定细胞发生反应并被消除，所产生的信号被传递到Th和Ts细胞。Ts细胞会抑制Th细胞的产生，两者共同刺激B细胞的产生，从而消除抗原使系统逐步达到平衡趋于正常。

基于上述反馈原理，现设第k代抗原(Ag)出现的数量为δ(k)，由正细胞Th和负细胞Ts对B细胞产生的刺激分别记为Th(k)和Ts(k)，B细胞所受的总刺激记为B(k)。

Th(k)=K1δ(k)

(9)

Ts(k)=K2f[B(k),ΔB(k)]δ(k)

(10)

式(10)中：K1为激励因子；K2为抑制因子；f()为非线性函数，表示T细胞所承受抑制量大小。

可得B细胞所受的总刺激表示为

B(k)=Th(k)-Ts(k)=

{K1-K2f[B(k),ΔB(k)]}δ(k)=

K{1-ηf[B(k),ΔB(k)]}δ(k)

(11)

式(11)中：K=K1为控制反应速度；η=K2/K1为控制稳态效果。

通过合理的调整η和K，可使本系统响应速度变快，超调量变小。

免疫反应的功能是既要保持系统的稳定，又要对入侵的抗原快速做出反应，这因为抗原会对生物本身造成伤害，需要对其立刻消除，然而抗体浓度过大也会对生物本身造成伤害，因此应进行调节控制，所以使生物本身所受伤害最小即为免疫系统的目标。同样在控制系统的动态调节中，其目的也是在保证系统本身的前提下可以迅速消除偏差，这与上述讨论的免疫系统目的是一致的，故将两个系统进行比较会得到相似之处如表1所示。

表1 免疫系统与控制系统的比较

通过比较控制系统与免疫系统的联系可知，式(11)可写为

U(k)=B(k)=KP1e(k)=

K{1-ηf[u(k),Δu(k)]}e(k)

(12)

式(12)中：KP1为比例系数。式(12)可以看作一个免疫控制器。

考虑常规PID控制算法为

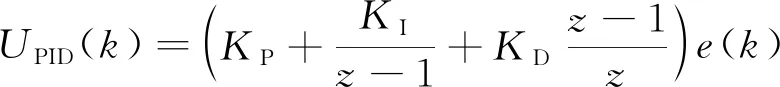
(13)

将免疫算法运用到PID控制中，可得免疫PID控制规律，即

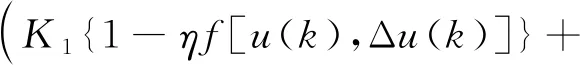
(14)

2.2 非线性函数f(·)的自适应调整

基于模糊控制器作为一个万能控制器，其可逼近任何非线性函数，所以可用该控制器构造[15]非线性函数f[u(k),Δu(k)]。

两个输入变量u(k)和Δu(k)是通过两个模糊集进行模糊化，两个模糊集表示为{正，负}，符号代表为{P，N}。输出变量f(·)的模糊化是通过三个模糊集进行，其模糊集表示为{正，零，负}，符号代表为{P，Z，N}。以上隶属函数均定义在整个实数集范围内,隶属度函数如图3、图4所示。

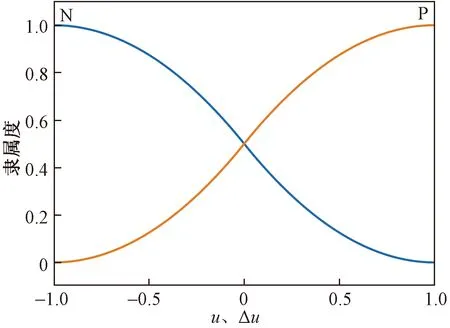
图3 输入变量u和Δu的隶属函数

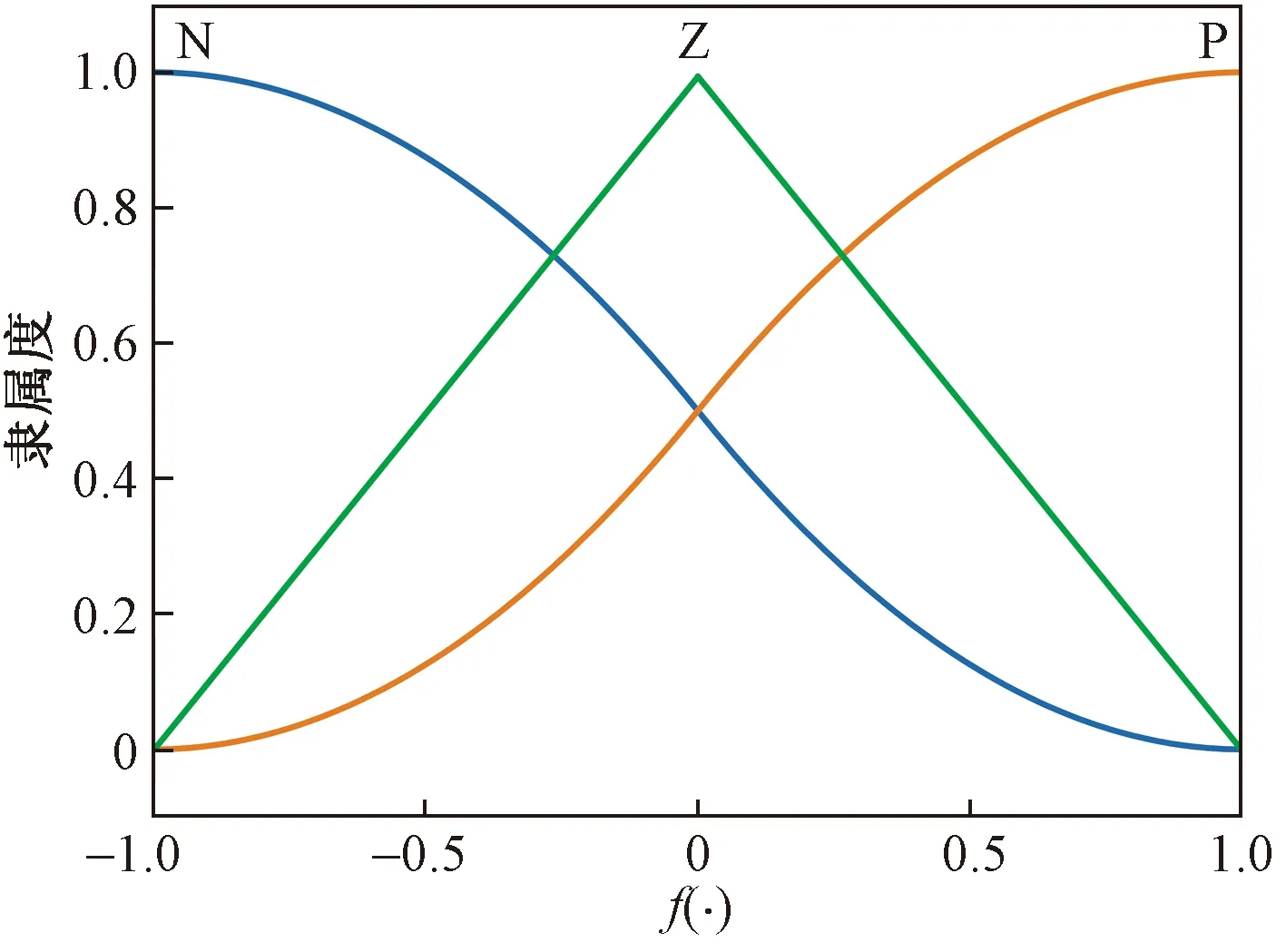
图4 输出变量f(·)的隶属函数

模糊控制器采用如下规则。

(1) ifuis P and Δuis P thenf(u, Δu) is N;

(2) ifuis P and Δuis N thenf(u, Δu) is Z;

(3) ifuis N and Δuis P thenf(u, Δu) is Z;

(4) ifuis N and Δuis N thenf(u, Δu) is P。

2.3 积分系数和微分系数的模糊调节

在PID控制理论中，比例环节调节系统的精度，积分环节减少系统的误差，微分环节改进系统的特性，但比例系数会随输出变化，微分和积分不是实时调整的，会使控制器不能满足系统的需求。为了满足张力偏差e(k)和偏差变化ec对系统的需要，使它拥有优良的特性，提高控制系统的自适应性，则通过模糊控制原理整定微分与积分系数，对比例系数采用免疫调节。使用Mamdani模糊推理及Centroid反模糊化法继续调节积分和微分系数，通过实时调整得到两个系数表达式为

(15)

式(15)中:KI和KD分别为积分和微分系数；KI0和KD0为控制器参数的初值；ΔKI和ΔKD为输出变量。

该模糊控制是以拉伸张力的设定值与实际值的偏差e(k)及偏差变化率ec作为输入，控制器中的积分和微分环节的变量ΔKI和ΔKD作为输出，输入及输出的子集均为{负大，负中，负小，零，正小，正中，正大}，子集中各元素的符号代表为{NB,NM,NS,ZO,PS,PM,PB}。

设定e和ec的论域均为(-3，3)；ΔKI的论域为(-0.3，0.3)；ΔKD的论域为(-3，3)。将规定好的数值经仿真后，得到输入变量e和ec的隶属函数以及输出变量ΔKI和ΔKD的隶属函数如图5、图6和图7所示。

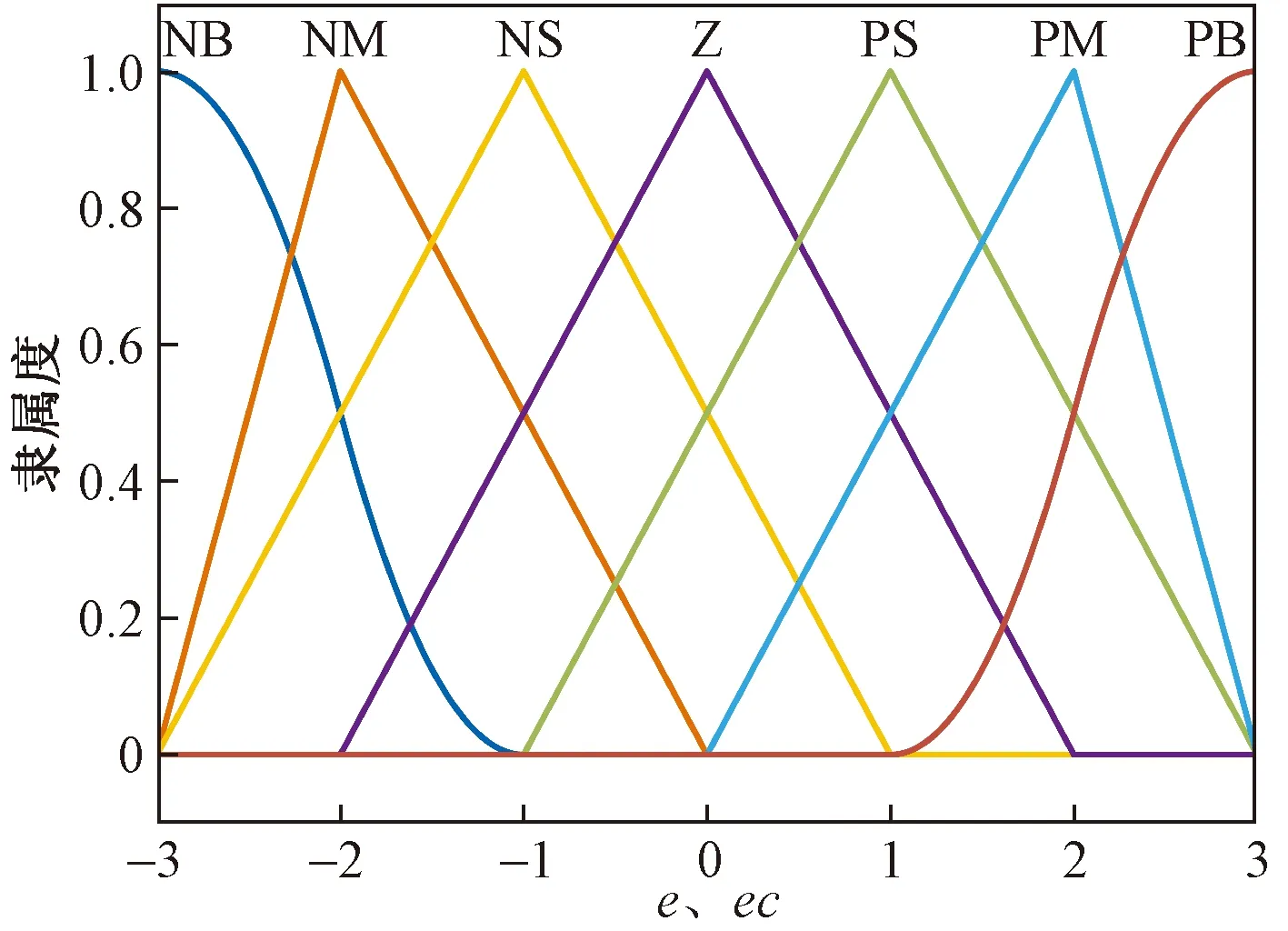
图5 输入变量e和ec的隶属函数

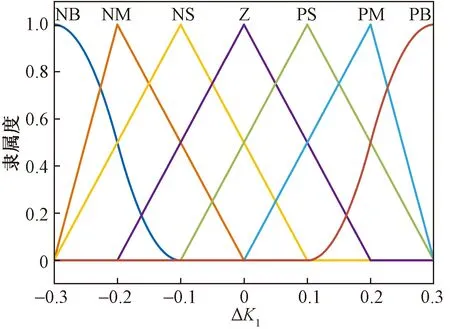
图6 输出变量ΔKI的隶属函数

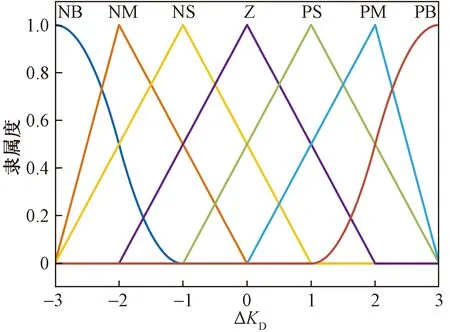
图7 输出变量ΔKD的隶属函数

根据生物免疫机制制定得到ΔKI和ΔKD的控制规则如表2所示。

表2 模糊控制规则表

综上所述，传统PID控制结合免疫机理以及模糊原理对其3个系数的调节使系统具有很好的适应性。结合式(9)～式(15)可得该控制器的总体控制式为

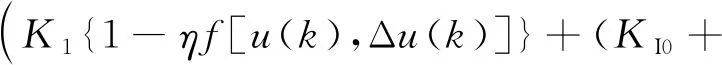
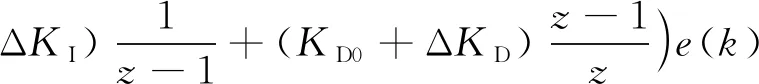
(16)

模糊免疫PID控制图如图8所示。

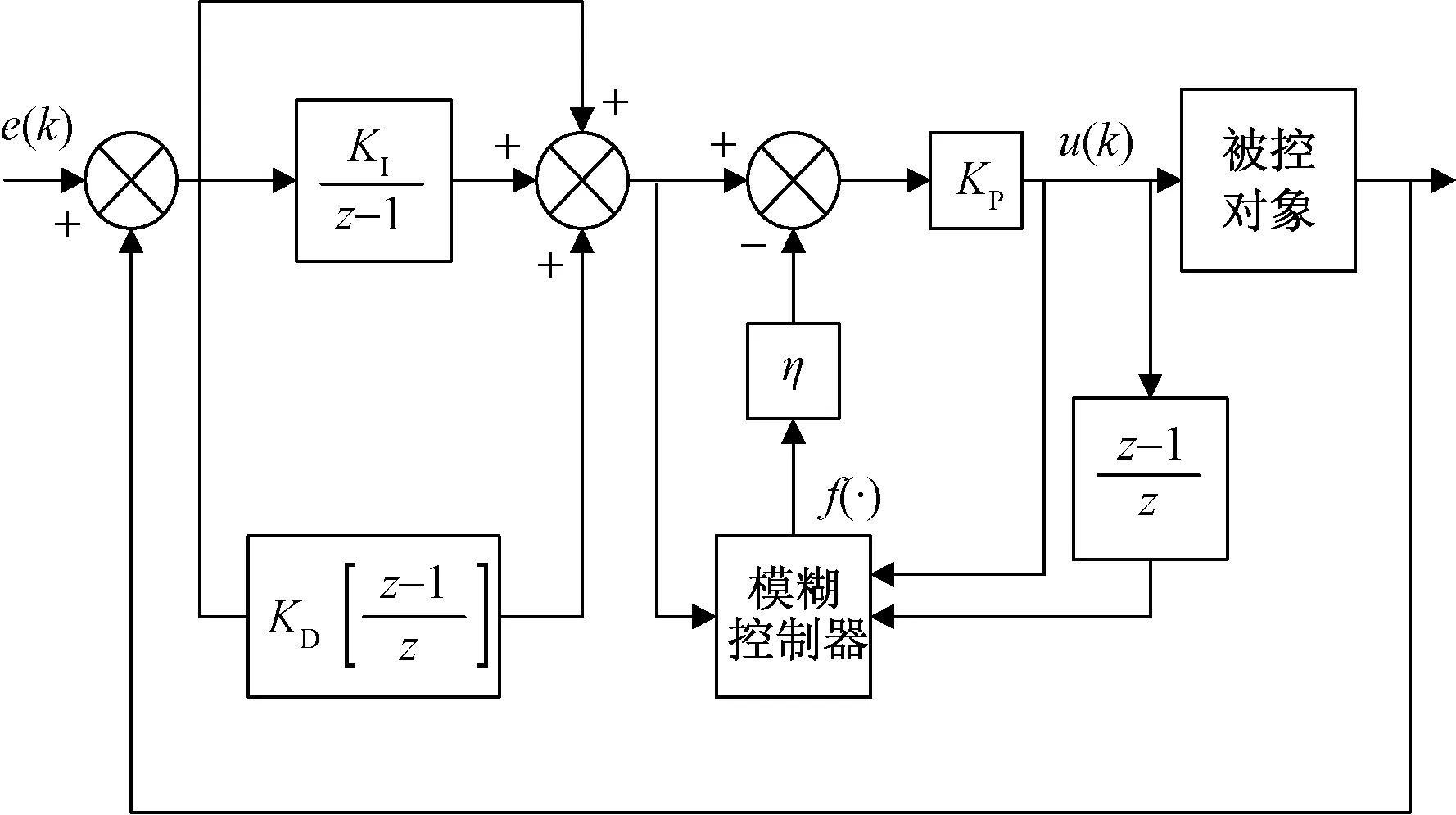
图8 模糊免疫PID结构图

3 仿真分析及实验验证

3.1 仿真分析

设定以25 N为定型机初始张力F，仿真总时间t=20 s，在设计本系统时，通过参数整定法整定一组PID参数：KP=3.8、KI=0.03、KD=1.34，模糊PID参数与PID算法设定值一致，通过免疫控制器和传统PID控制器的增益关系调整免疫控制器的参数：K=0.8、η=0.4。根据上述得到的参数通过MATLAB软件分别对常规PID，模糊PID及模糊免疫PID进行仿真对比分析，观察其达到稳定时间的快慢以及震荡的幅度，以此验证三种算法的优越性。将三种算法的仿真结果导出曲线图，仿真对比结果如图9所示。

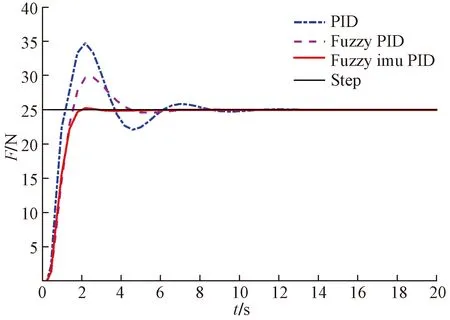
图9 三种算法仿真曲线

由图9可以看出，在定型过程中拉伸张力在三种算法控制下得到的波动是不同的，在常规PID控制下到达稳定时间在10 s左右，超调量达到38.2%，这在生产中绝对不被允许的，会使织物定型不均，出现折痕甚至撕裂，严重情况下可能会造成机器损坏。在模糊PID控制下，较常规相比系统的超调量明显下降，调节时间也降低到6 s左右，但超调仍有17.8%，由于本系统要求超调量在5%以下，因此模糊PID控制仍有较大的不足。通过仿真发现在模糊免疫PID控制时，系统超调量只有1.6%左右，基本接近无超调，到达稳定时间也较快，满足产品生产中的要求，也极大改善了系统的性能。

在实际生产中，外部环境的变化也会对张力控制系统产生影响，为了验证本系统的抗干扰性能，在12 s时加入阶跃扰动，仿真曲线如图10所示。

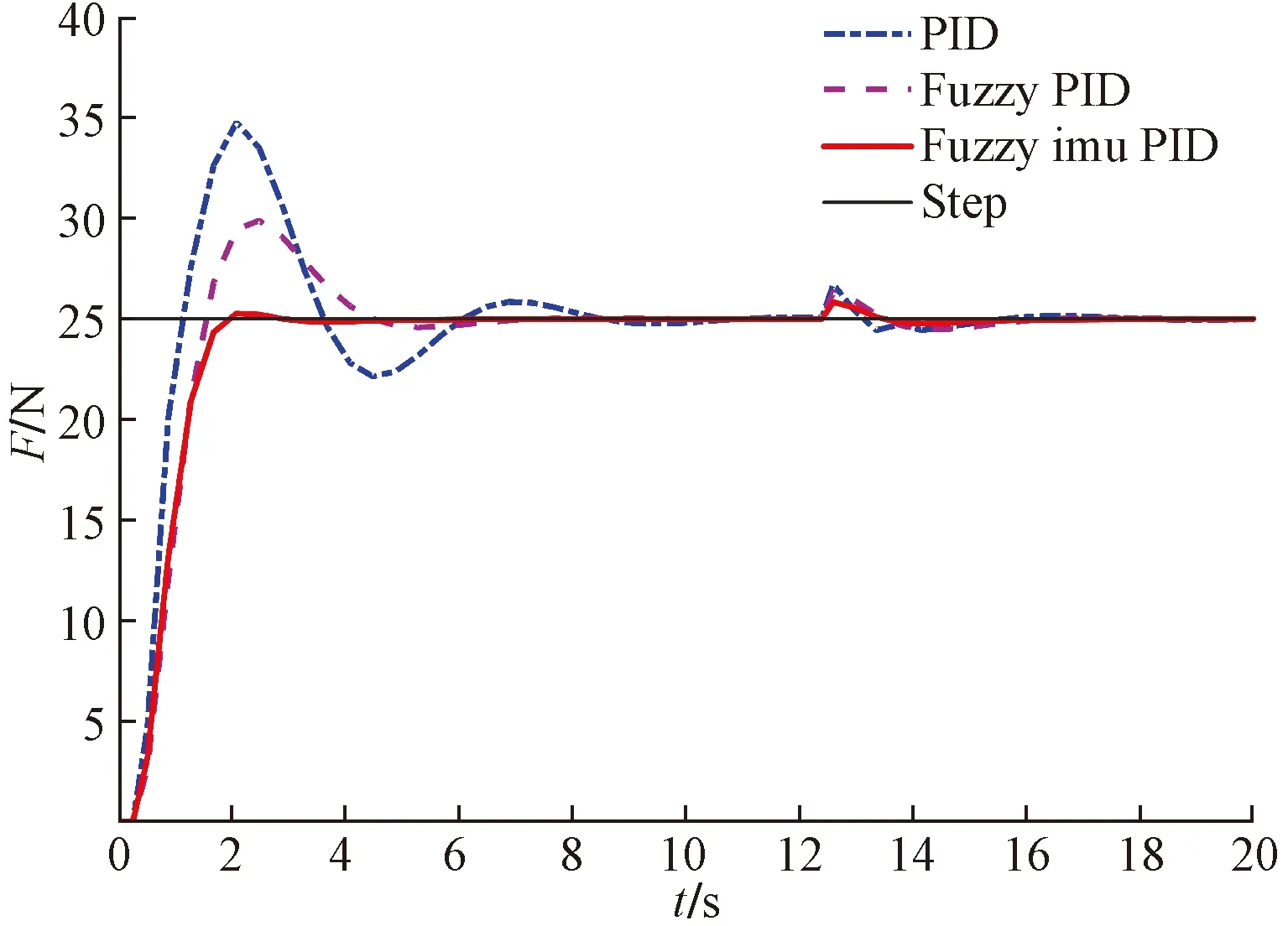
图10 加入扰动后三种算法仿真曲线

通过仿真曲线的分析，常规PID不能较快达到稳定，超调依然较大，不能及时对扰动做出调整。模糊PID达到稳定时间比常规PID快，但震荡依旧较大。利用模糊免疫PID控制时，张力所受扰动的影响较小，能及时做出调整到达稳定，抗干扰性能有了很大的提升。

根据拉伸张力数学模型可知，速度变化对张力具有直接影响，为对优化后的模糊免疫PID控制器性能进一步验证，现选取系统稳定运行后的某个10 s阶段作为仿真对象，将在4 s时加入一个幅值为20 r/min，频率为1 Hz的正弦信号作为模拟速度的干扰，由于前述已经介绍了到达稳定状态的情况，因此只观察速度波动的影响，将模糊免疫PID分别于常规PID和模糊PID进行对比分析，观察拉伸张力在不同控制器下的响应曲线如图11所示。

由图11可知，当运行速度发生变化时，在模糊免疫PID控制下，拉伸张力仅出现微小的波动，几乎可以忽略不计。但是在常规PID和模糊PID控制下，伴随速度的变化张力都会出现明显的波动，通过对比图11(a)、图11(b)的曲线可知，相较于常规PID和模糊PID控制，该控制器具有更强的抗负载干扰能力。

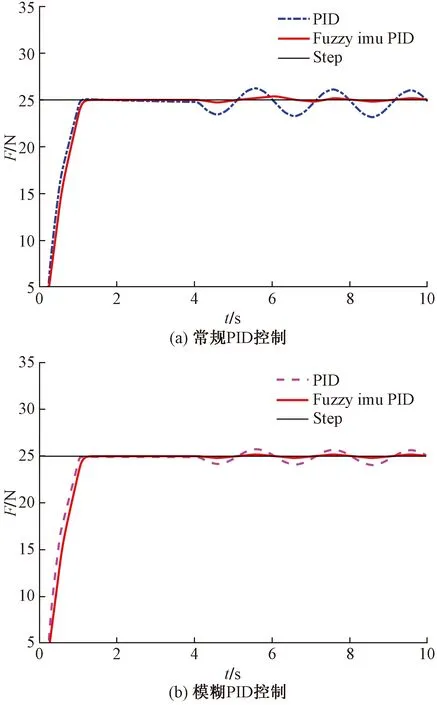
图11 速度波动时张力变化对比曲线

3.2 实验验证

为了证明该控制器的可行性，测试模糊免疫PID控制器对定型机拉伸张力系统的控制效果，对本系统进行张力控制实验。在实验操作中，张力偏差e和偏差变化率ec是使用Step7软件编程进行判断的，用于输入和输出的模糊控制规则表通过PLC编程存储在数据块中，根据数据块中调用适当的参数来收集和处理现场数据，搭建实验平台对本张力系统进行验证，实验平台如图12所示。

图12 实验平台

由图12可知，本实验平台主要由控制面板、张力传感器、拉伸装置、牵出装置以及扎辊等组成，其采用三菱张力传感器LX-005TD，通过Frofibus-DP作为控制器与设备之间的连接，同时带有精简系列控制面板，样机配备了西门子S7-300PLC，可搭配模糊免疫PID算法对张力进行控制。通过张力传感器获得的张力信号，与张力初始值比较得到偏差，利用PLC对偏差进行数据处理，输出控制信号传递给被控对象，完成实验进程。

选择幅宽为30 cm的织物，张力初始值设置为25 N，采样时间为70 s，每隔5 s记录一组数据，比较改造前后的实验结果，即常规PID和模糊免疫PID算法的对比分析。现将具体实验数据输入到如表3所示。

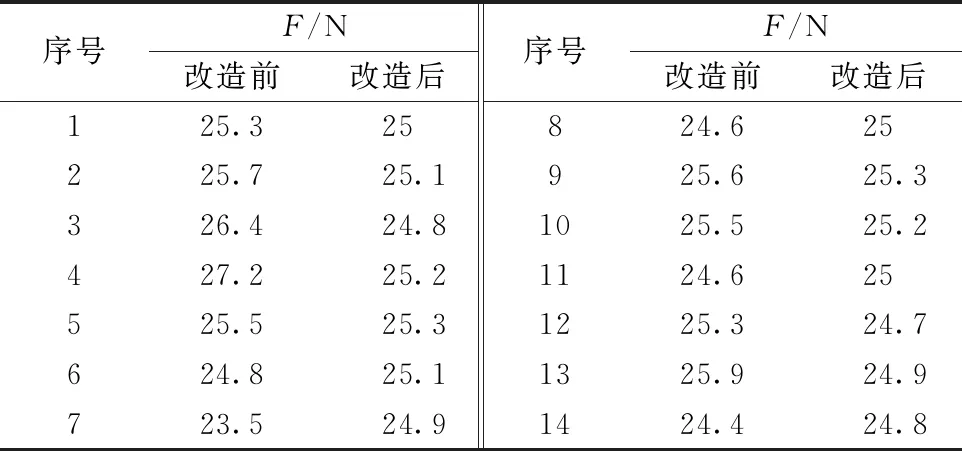
表3 实验数据

为便于观察本系统改造前后张力的变化情况，将实验数据绘制成折线图如图13所示。

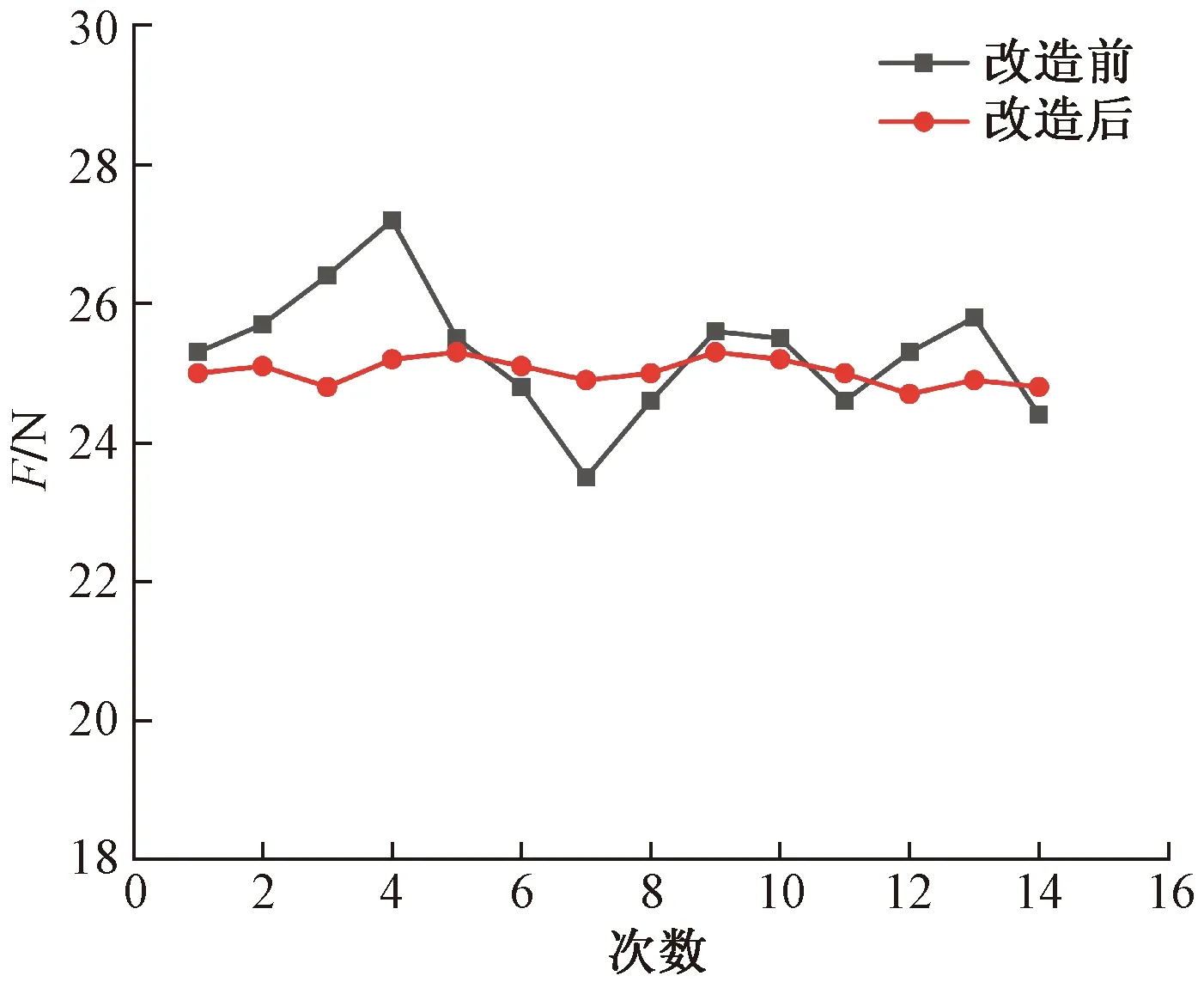
图13 张力分析实验图

由图13可知，改造前本系统即PID控制张力波动较大，振幅明显，本文设计的模糊免疫PID控制器下的张力始终在一定范围内变化，控制精度控制在2%以内，满足系统的要求。

4 结论

本文设计了模糊免疫PID控制器，将该控制器运用在定型机张力控制系统中，通过拉伸张力数学模型，再结合MATLAB分析验证并搭建仿真模型得出仿真结果可得如下结论。

(1)使用常规PID进行控制时，被调量不能及时反映系统受到的扰动，到达稳定时间也很慢，不能有效抑制系统内外因素变化引起的张力波动，无法保证高精度控制要求。

(2)模糊PID控制虽然可以使人们的操作经验和专家知识以规则的形式存在于系统中，但是它们缺乏自学习能力。由仿真结果可知，相比PID控制，系统性能虽然提高了很多，但还是存在超调量偏大与调节时间增加的问题。

综上，模糊免疫PID控制就是把常规PID与模糊控制结合起来，综合了模糊控制善于处理非线性问题和免疫具有自学习能力的优点，可以改进拉伸张力系统的弊端，更好地满足生产的需要。