不同卸荷路径下的页岩蠕变特性试验研究

王空前， 谢东武

(1.郑州财经学院土木工程学院， 郑州 450000； 2.同济大学土木工程学院地下建筑与工程系， 上海 200092)

岩石流变力学与地下硐室设计、施工和运营安全紧密关联，同时也是当下的研究热点内容之一[1-2]。地下硐室围岩在受扰动前处于三向应力状态，工程实践表明硐室开挖后岩体时效变形显著，围岩随着时间发展，变形位移不断累积，最终可能导致硐室坍塌，因此研究岩石三轴卸荷蠕变特性具有重要意义[3-4]。本研究背景为某深埋矿井巷道，巷道开挖后围岩蠕变现象显著，最终导致塌方，故而研究岩石的卸荷蠕变力学特性很有必要。

目前关于岩石卸荷蠕变特性的研究已取得一定成果：张龙云[5]以花岗岩为研究对象，开展三轴卸荷流变试验，研究其卸荷流变变形、速率和强度等变化；石振明等[6]以绿片岩为试验对象，设计恒定轴压分级卸围压应力路径下，开展蠕变试验，分析轴向、侧向蠕变规律；黄兴等[7]开展砂质泥岩恒轴压逐级卸围压蠕变试验，研究卸荷流变中偏应力-应变关系及流变应变变化规律，分析砂质泥岩的扩容效应；杨超等[8]针对裂隙大理岩试样，开展恒轴压分级卸围压三轴卸荷蠕变试验，研究试样在不同裂隙倾角下的卸荷蠕变应变，探索完整岩石与裂隙岩体间卸荷蠕变的相关关系。目前卸荷应力路径下的岩石蠕变特性研究相比常规加载应力路径下较少，开展岩石卸荷蠕变试验是系统性认识岩石流变特性的有效途径之一。

由于目前的岩石卸荷流变试验多为恒轴压卸围压的应力路径，与工程实践中应力释放方式存在一定偏差，故设计轴压与围压等比卸荷的应力路径，与传统应力路径进行对比试验。其中，等比卸荷即径向应力σ3与轴向应力σ1之比σ3/σ1为常数，该应力路径多见于高边坡、地下硐室，此类工程大部分区域内岩体开挖期间主应力比为常数[5]。现依托于某深埋矿井巷道工程实践，以顶板页岩为研究对象，开展不同卸荷路径下的蠕变试验，对比分析页岩的轴向和侧向应变特征、应变速率及长期强度，研究成果可为地下硐室长期稳定性研究提供一定参考。

1 页岩卸荷蠕变试验设计

1.1 试样制备及基本力学参数

试样取自某深埋矿井巷道顶板新鲜页岩，岩层为志留系上统沙帽组，岩块呈黑褐色层状，岩样基本物理力学参数如表1所示。

表1 岩样基本物理力学参数

为了研究页岩在三向应力强度特性，采用TLW-2000型岩石三轴流变试验仪，将岩样加工成φ50 mm×100 mm的圆柱样(图1)，开展三轴压缩试验，围压设置为20 MPa，轴向应力σ1与轴向应变ε1关系曲线如图2所示。

图1 岩石试样照片

由图2可看出，页岩试样A-1和A-2在围压20 MPa下的最大轴向应力分别为106.46 MPa和99.42 MPa，其平均值为102.94 MPa。

图2 应力-应变曲线

1.2 卸荷蠕变试验设计

卸荷蠕变试验采用与三轴压缩试验相同的TLW-2000型岩石三轴流变试验仪，设计两种应力路径：应力路径Ⅰ为恒轴压卸围压，应力路径Ⅱ为轴压和围压等比卸荷。应力路径示意图如图3所示。

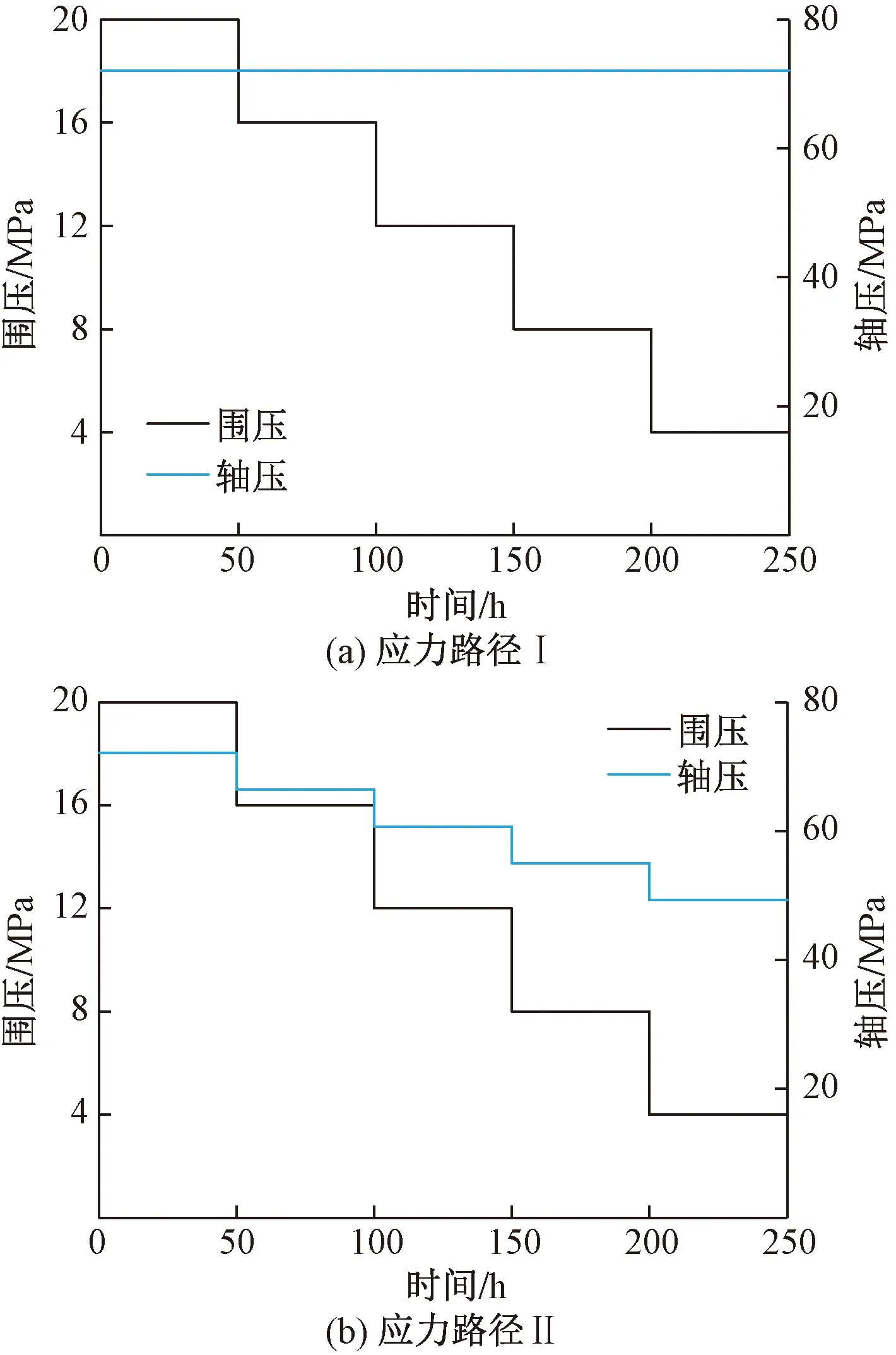
图3 应力路径图

应力路径Ⅰ：初始围压设置为20 MPa，初始轴压取页岩三轴试验中最大轴向应力平均值的70%，即72.1 MPa。初始轴压保持不变，围压以4 MPa为应力梯度进行卸载，直至试样破坏。步骤为：首先以0.1 MPa/s的速率加载围压σ3到20 MPa，应力稳定后以0.1 MPa/s的速率加载轴压σ1到72.1 MPa。轴压σ1达到目标值后，观察岩样的轴向、侧向位移，当其稳定后，保持轴压恒定，以0.1 MPa/s的速率卸载围压，每4 MPa为一个应力梯度，每卸一级围压，至少保持50 h时间使蠕变变形充分发展，然后再继续卸载，直至岩样破坏。

应力路径Ⅱ：初始围压设置为20 MPa，初始轴压取页岩三轴试验中最大轴向应力平均值的70%，即72.1 MPa。围压以4 MPa为应力梯度进行卸载，轴压以同样比例(σ3/σ1=70%)进行卸载，即5.7 MPa，围压和轴压等比卸荷，直至试样破坏。步骤为：首先以0.1 MPa/s的速率加载围压σ3到20 MPa，应力稳定后以0.1 MPa/s的速率加载轴压σ1到72.1 MPa。轴压σ1达到目标值后，观察岩样的轴向、侧向位移，当其稳定后，保持轴压恒定，以0.1 MPa/s的速率同时卸载围压和轴压，围压以4 MPa为应力梯度进行卸载，轴压以5.7 MPa为应力梯度进行卸载，每一级卸载后至少保持50 h时间使蠕变变形充分发展，然后再继续卸载，直至岩样破坏。

1.3 卸荷蠕变试验结果

两种应力路径下的页岩卸荷蠕变试验结果如图4、图5所示，其中图4为页岩在应力路径Ⅰ下的(恒轴压卸围压)轴向、侧向应变随时间累积曲线，图5为页岩在应力路径Ⅱ下的(等比卸荷)轴向、侧向应变随时间累积曲线。

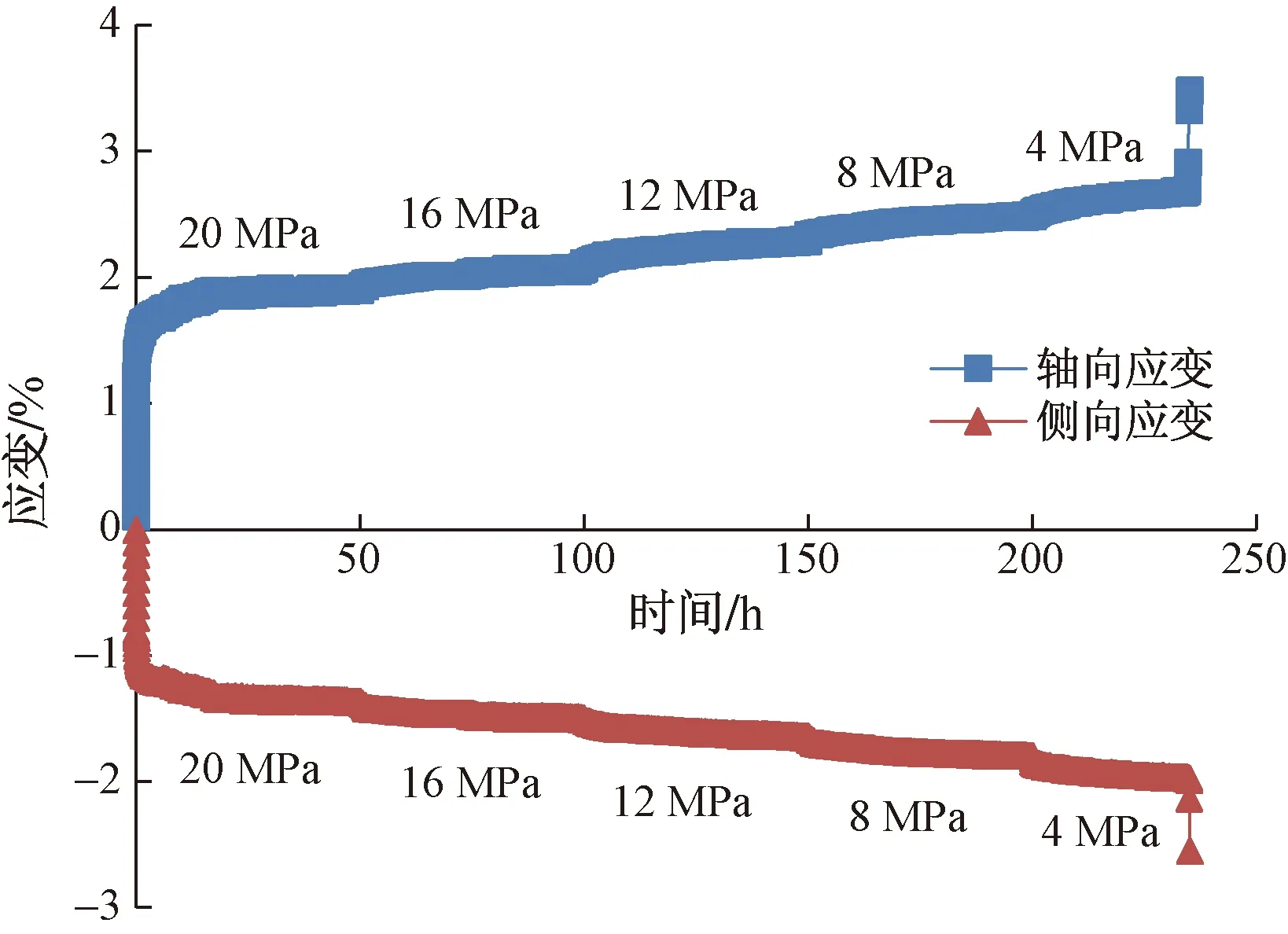
图4 恒轴压卸围压蠕变曲线

图5 等比卸荷蠕变曲线

由图4可看出，在轴压恒定(72.1 MPa)的条件下，从20 MPa开始逐级卸载围压(4 MPa为应力梯度)，至第5级应力水平时岩石屈服破坏。此时，历经234.52 h轴向应变达到最大值3.481×10-2，侧向应变达到最大值-2.549×10-2。

由图5可知，轴压从72.1 MPa开始逐级卸载(应力梯度为5.7 MPa)，围压从20 MPa开始逐级卸载(4 MPa为应力梯度)，至第5级应力水平时岩石屈服破坏。此时，历经217.55 h轴向应变达到最大值0.683×10-2，侧向应变达到最大值-0.345×10-2。

综合图4、图5可知，页岩在应力卸荷条件下具有显著的流变特性，在应力路径Ⅰ、Ⅱ下的卸荷蠕变曲线形态基本一致。页岩的轴向、侧向应变均由瞬时应变和蠕变应变组成，在第1～4级加卸载等级下，页岩蠕变出现衰减及稳定蠕变阶段，直至最后一级应力，页岩发生加速蠕变行为，岩石宏观破坏。

2 试验结果分析

2.1 卸荷蠕变曲线分析

通过Boltzmann线性叠加[9-10]处理图4、图5后得到分别卸载蠕变曲线，如图6所示。

分析图6(a)、图6(b)，应力路径Ⅰ下的轴向、侧向应变差异在1.5倍以内，每一级轴向应变量值皆大于侧向应变。在应力路径Ⅰ条件下，岩石到达最后一级应力水平前，轴向应变为2.488×10-2，侧向应变为-1.797×10-2，在破坏围压应力下分别增长为3.481×10-2和-2.549×10-2，增长部分分别占轴向和侧向总应变的28.53%和29.50%。侧向应变的变化程度大于轴向应变，体现出页岩卸荷蠕变的扩容现象，侧向扩容相较轴向扩容更为明显。

再分析图6(c)、图6(d)，等比卸荷条件下的轴向和侧向应变量值相差不大，差异在2倍以内，每一级轴向应变量值皆大于侧向应变。在应力路径Ⅱ条件下，岩石到达最后一级应力水平前，轴向应变为0.429×10-2，侧向应变为-0.201×10-2。与应力路径Ⅰ不同之处在于轴向应变发生瞬时卸荷回弹，轴向应变在第5级卸载瞬间从0.458×10-2变为0.445×10-2，随即累积直至0.683×10-2，侧向应变未见卸荷回弹现象，直接从-0.201×10-2变为-0.345×10-2。最后一级应力水平下，轴向、侧向应变的增长分别占轴向、侧向总应变的38.31%和41.74%，侧向扩容相比轴向扩容更为显著。

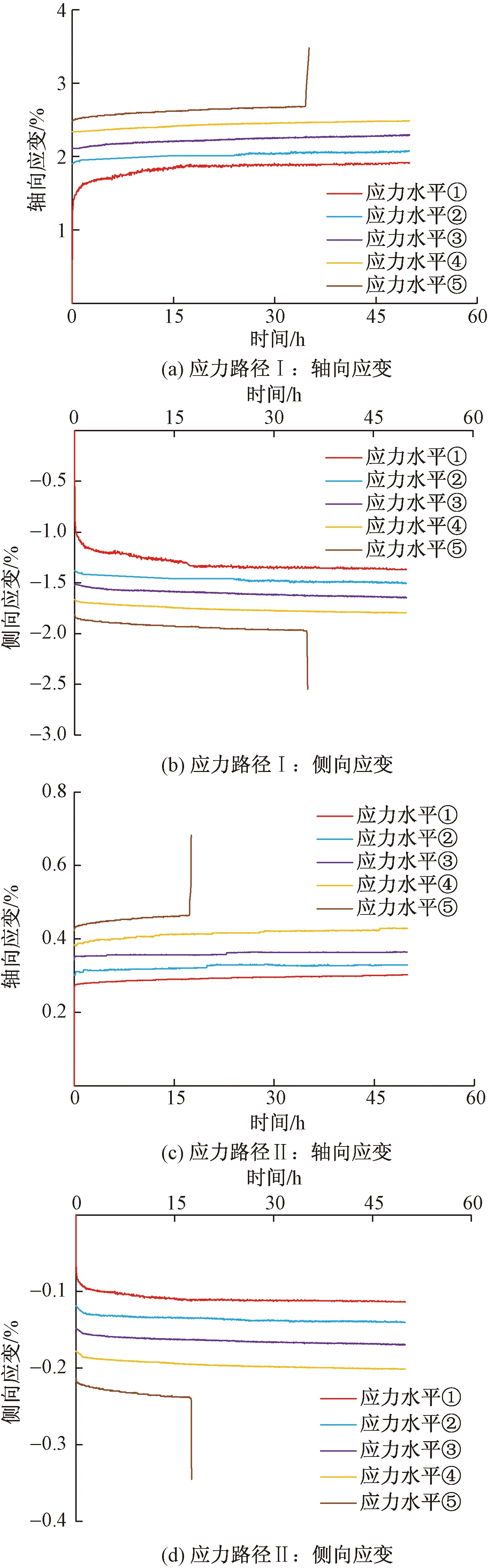
图6 分别卸荷蠕变曲线

综合图6分析，两种应力路径下的分别卸载蠕变曲线特征大致相同，均在卸载瞬间产生瞬时轴向和侧向应变，且第1级卸载产生的瞬时应变最大。分析两种应力路径下的第1级衰减蠕变阶段，应力路径Ⅰ下的衰减蠕变阶段形态总体上相比应力路径Ⅱ更为显著，且历时更长。在第1级卸载下，瞬时应变远大于第2～5级，分析其原因可能为：页岩自身发育一定微裂纹，微裂纹在应力场作用下处于较稳定的阶段，当卸去部分荷载后，岩石弹性骨架的弹性变形性质得到发挥，微裂纹瞬间扩展，导致瞬时应变显著增大。

2.2 瞬时、蠕变应变特征

将两种应力路径下的页岩瞬时、蠕变应变进行统计，如表2所列。图7、图8分别为岩石瞬时应变和蠕变应变对比曲线，由图6可知在两种应力路径下，第1级轴向、侧向瞬时应变远大于第2～5级，为了便于观察第2～5级瞬时应变变化规律，图7中省去第1级瞬时应变。

图8 蠕变应变对比曲线

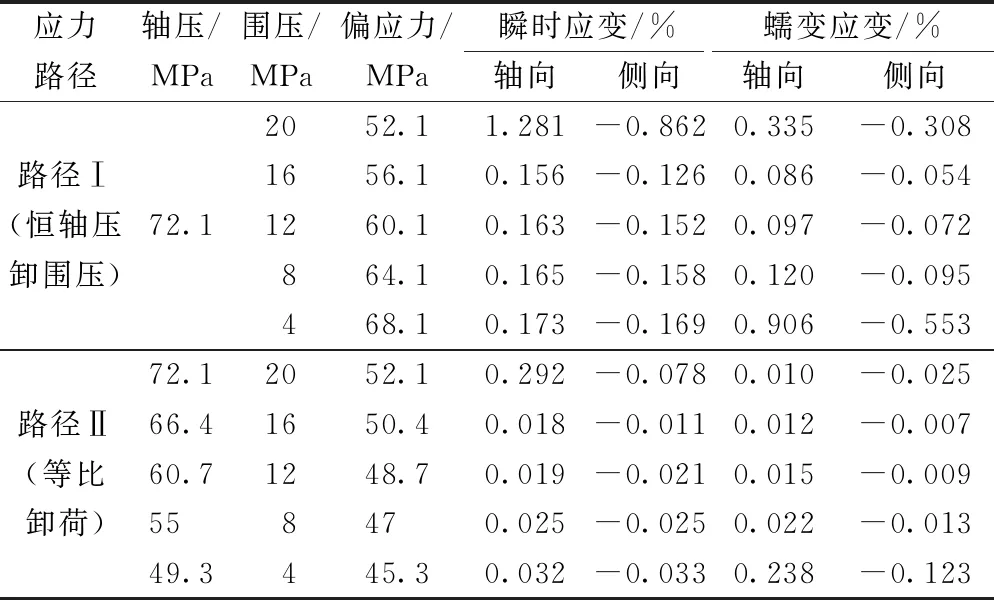
表2 两种应力路径下页岩瞬时、蠕变应变

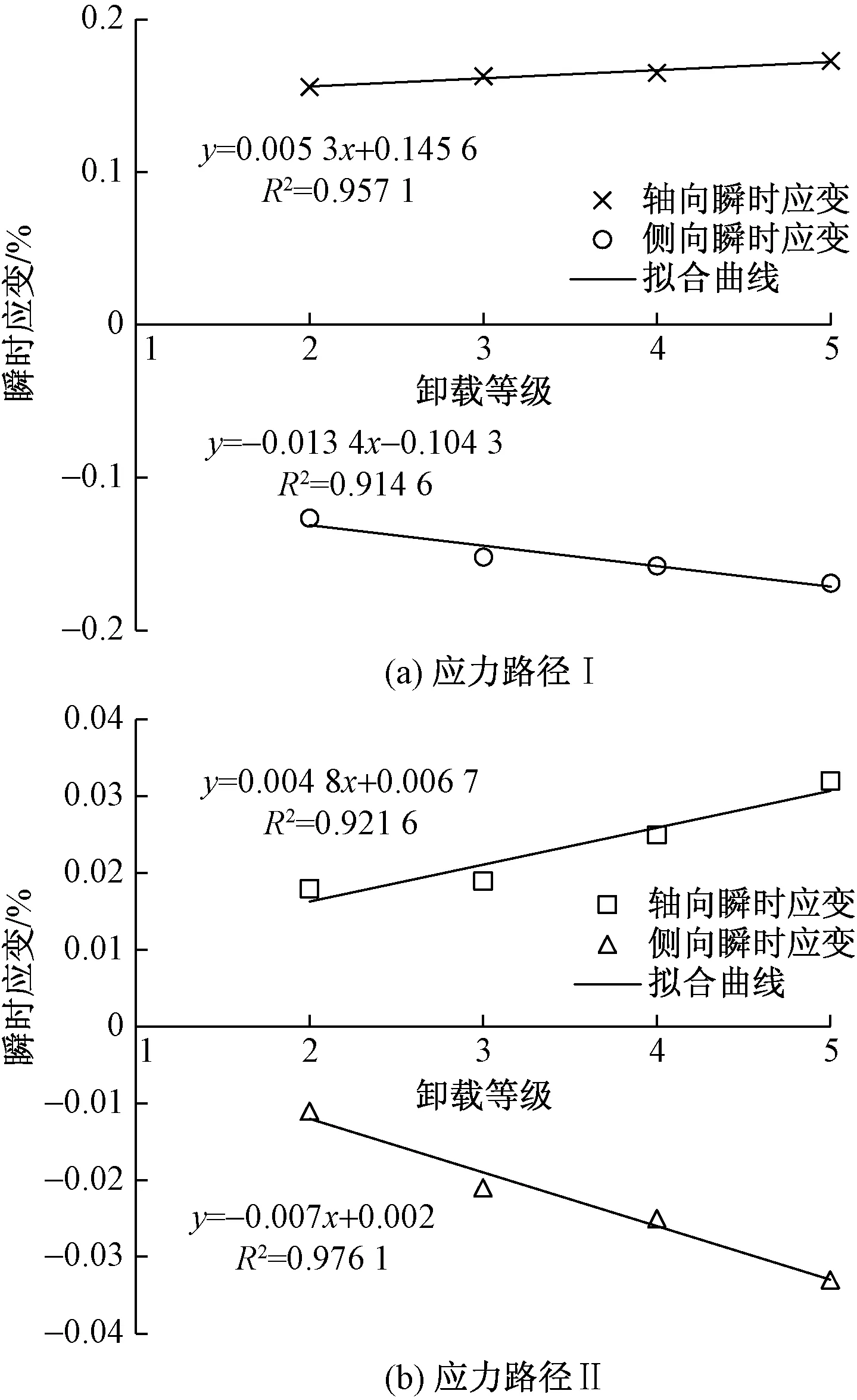
图7 瞬时应变对比曲线

由表2可知，应力路径Ⅰ第1级轴向、侧向瞬时应变分别为1.281×10-2和-0.862×10-2，再结合图7(a)中第2～5的应变节点可知，在同一卸载等级下，应力路径Ⅰ下的页岩的轴向瞬时应变量值均大于侧向，轴向瞬时应变的线性增长趋势略小于侧向瞬时应变。应力路径Ⅱ第1级轴向、侧向瞬时应变分别为0.292×10-2和-0.078×10-2，图7(b)中第2～5级侧向瞬时应变量值均小于轴向，侧向瞬时应变的线性增长趋势大于轴向瞬时应变。综合图7可得，第2～5级轴向、侧向瞬时应变均随卸载等级的增加呈线性增大趋势。

由图8可看出，在恒轴压卸围压条件下，轴向、侧向蠕变应变从第1～2级先减小，第2～4级缓慢递增，最后一级急剧增大。而在等比卸荷条件下，第1～4级轴向、侧向蠕变应变缓慢递增，最后一级显著增大。再由图2和表3可知，应力路径Ⅰ的偏应力递增，应力路径Ⅱ的偏应力递减，故而在两种应力路径下，岩石轴向、侧向蠕变应变从第1～2级的变化规律差异显著。

2.3 蠕变速率

张春阳等[11]针对逐级增量加载蠕变试验提出蠕变速率求取方法，由于本文中卸荷蠕变试验亦是逐级卸载，所以可参考张春阳等[11]提出的求取方法，即

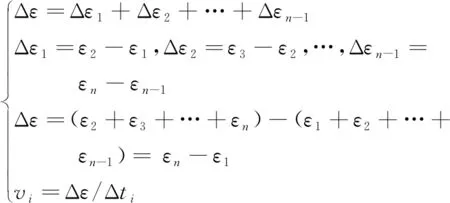
(1)

式(1)中：ε为蠕变应变；Δti为蠕变时间；n为蠕变试验数据个数；vi为应变速率。

由于图5、图6中的蠕变曲线簇性态较为相似，第1～4级加卸载等级未发生加速蠕变，故以最后一级应力水平下的蠕变曲线为研究对象，通过式(1)的方法计算蠕变速率并绘制成图，如图9所示，限于篇幅，仅给出应力路径Ⅰ下的第5级蠕变速率曲线。

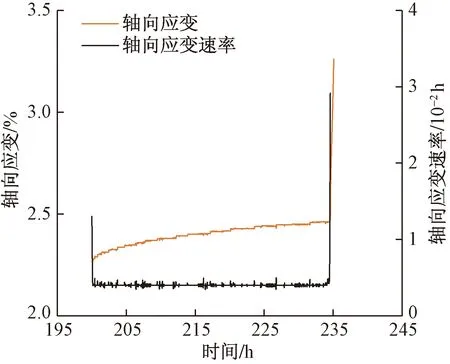
图9 应力路径Ⅰ：轴向蠕变速率曲线

由图9可看出，应力路径Ⅰ下的最后一级轴向蠕变速率先由某一数值(初始蠕变速率为1.302×10-2h)快速降低，接着在较长时间内保持恒定(稳态蠕变速率为0.409×10-2h)，最后急剧升高至一个最大值(极限加速蠕变速率为2.916×10-2h)，岩样破裂。为了细致观察页岩加速蠕变阶段及其与稳定蠕变阶段的“过渡区间”[12]的蠕变速率变化规律，选取两种应力路径的轴向、侧向蠕变速率局部节点绘制成图，如图10所示。

图10 蠕变速率局部曲线

由图10可看出，在岩石加速蠕变阶段及其与稳定蠕变阶段的“过渡区间”，蠕变速率先微降，再保持相对稳定，最后急剧增加。应力路径Ⅰ中，这个过程仅持续0.71 h，轴向、侧向应变分别达到0.778×10-2和0.575×10-2。而在应力路径Ⅱ中，“过渡区间”和加速蠕变阶段仅持续5.66 h，轴向、侧向应变分别达到0.215×10-2和0.099×10-2。这说明岩体开挖卸荷后，当达到破坏应力水平后，围岩可能发生大变形等不良现象，工程实践中应做好监测工作。

两种应力路径中，侧向蠕变速率都高于轴向，是轴向的2～2.5倍，岩石侧向扩容不可忽视。等比卸荷的蠕变速率及蠕变变形皆不及恒轴压卸围压，且等比卸荷的轴向应变在从第4～5级应力水平下发生回弹，这说明岩石在应力路径Ⅱ(等比卸荷)中发生卸荷蠕变破坏的可预见性较小，围岩监测时应引起重视。

2.4 长期强度

岩石逐级增量加载蠕变研究中，等时应力-应变曲线簇法是一种应用广泛的长期强度求取方法[13-15]，由于本文中卸载蠕变试验也是逐级进行应力卸载，且通过Boltzmann线性叠加原理进行数据处理，得到了分别卸载蠕变曲线(图6)，所以亦可通过等时应力-应变曲线簇法基于图6确定页岩卸载蠕变的长期强度。选取0～50 h共6个时间节点，其中0 h为时间趋近于0的某一节点，以应力路径Ⅰ为例，等时偏应力-应变曲线如图11所示。

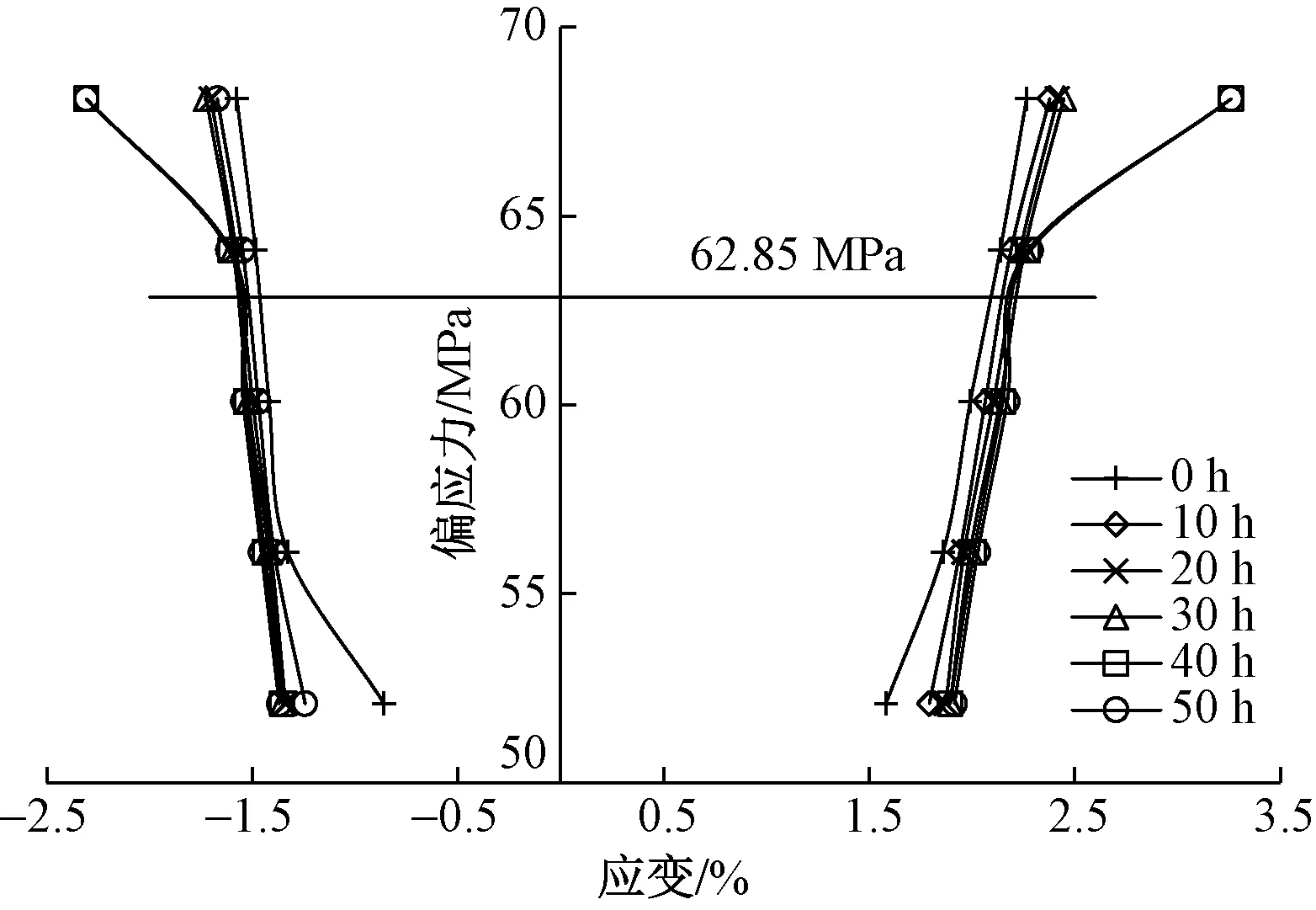
图11 应力路径Ⅰ：等时偏应力-应变曲线

在图11蠕变曲线簇中取拐点，确定应力路径Ⅰ条件下页岩卸载蠕变长期强度为62.85 MPa。通过同样的方法，确定应力路径Ⅱ中长期强度为 47.69 MPa，相比应力路径Ⅰ低15.16 MPa，页岩三轴压缩强度为102.94 MPa，长期强度在应力路径Ⅰ和Ⅱ条件下分别折减了38.95%和53.67%，这说明岩石在等比卸荷应力条件下更易屈服破坏。

3 结论

(1)岩石在轴压、围压等比例卸荷及恒轴压卸围压应力条件下，岩石蠕变发展趋势基本一致，岩石屈服破坏前均经历衰减、稳定蠕变阶段，当应力条件达到破坏应力水平时，岩石发生加速蠕变行为。

(2)在两种应力路径下，页岩每一级应力水平的轴向应变量值皆大于侧向应变。在达到最后一级应力水平前，侧向应变的变化程度大于轴向应变，体现出页岩卸荷蠕变的扩容现象，侧向扩容相较轴向扩容更为明显。

(3)两种应力路径中，侧向蠕变速率都高于轴向，是轴向的2～2.5倍。等比卸荷的轴向、侧向蠕变速率和变形量都不及恒轴压卸围压，且等比卸荷的轴向应变在从第4～5级应力水平下发生回弹，这说明岩石在应力路径Ⅱ(等比卸荷)中发生蠕变破坏的可预见性较小，围岩监测时应引起重视。

(4)页岩在恒轴压卸围压和等比卸荷应力路径中，长期强度分别为62.85 MPa和47.69 MPa，岩石在等比卸荷应力条件下更易屈服破坏，工程实践中应考虑长期强度折减问题。

(5)本文研究背景为流变现象显著的深埋矿井巷道围岩，建议施工过程采取必要的支护及监测手段，削弱岩体卸荷引起的时效变形，以维持地下硐室的长期稳定性。