基于CUDA架构并行算法的带地形AMT二维反演实现与应用

韩思旭， 陈小斌， 陈卫营， 罗 强， 宋婉婷

(1.广东省地球物理探矿大队， 广州 510800; 2.广东省地质物探工程勘察院， 广州 510800; 3.中国地震局地壳应力研究所， 北京100085; 4.中国科学院地质与地球物理研究所， 中国科学院矿产资源研究重点实验室， 北京 100029)

音频大地电磁法(audio-frequency magnetotelluric method，AMT)通过观测和处理天然电磁场信号获取地下一定范围内的电性结构分布，具有频带宽(0.1 Hz～100 kHz)、探测深度大、对二维构造反应明显、施工轻便等优势，已成为矿产勘探、油气调查、工程勘查等领域的重要地球物理探测工具[1]。反演是AMT资料处理过程中的关键步骤。目前，二维反演是AMT数据处理实际应用中最为有效和普遍的手段，如何提高二维反演精度与速度是保障探测结果解释可靠性和提升数据处理效率的关键问题[2]。

AMT数据的二维反演和一维反演在反演原理和反演方法上并无本质区别, 只是二维反演处理的不再只是单个测点上的数据, 而是包含整条测线(垂直于构造走向) 上所有测点的数据，并且还需同时考虑介质电性在纵向和横向两个方向上的变化，因此二维反演需要拟合的数据量大大增加[3]。此外，相较于一维反演，二维反演处理的观测参数更多, 如TE(transverse-electric)和TM(transverse-magnetic)两个极化方向的电阻率和相位，或者由垂直磁场计算而来的倾子Tipper等[4]，这就使得模型数据相对参数的偏导数矩阵(雅可比矩阵)的阶数较大, 造成计算量大幅上升。因此在处理大网格、多频率模型时，二维反演需要较长的计算时间。二维反演的主要计算量来自于二维正演计算及偏导数矩阵的计算。为此，众多学者提出了多种快速二维反演方法，从二维正演或雅可比矩阵计算入手，发展了降低计算量、提升计算速度的方法[5-8]，极大地推动了AMT二维反演的实用化。

随着高性能计算机特别是并行计算技术的蓬勃发展，利用并行计算能力成为实现高精度、快速度AMT数据反演的一种可行手段[9-10]。最先发展起来的并行计算方式主要基于多核CPU(central processing unit)进行，其中代表性的是基于MPI(message passing interface)环境的并行计算，大量的研究成果显示出并行计算在电磁正反演中的良好加速效果[11-15]。但是，受CPU核数限制，这种并行计算的实现往往需要借助超级计算机或者计算机集群，造成计算成本较高[16]，同时CPU程序逻辑的复杂度也限定了程序执行的指令并行性。而GPU(graphics processing unit)的最大特点是它拥有超多计算核心，且每个核心都可以模拟一个CPU的计算功能。目前GPU已经发展为多线程多核处理器，具有强大的并行计算能力，近年来将GPU并行计算能力与实际的科学工程计算需求相结合已表现出巨大的潜力[17-19]。尤其是2006年NVIDIA公司为实现GPU通用计算提出编程统一计算设备架构(compute unified device architecture，CUDA)后，使得在科学计算中一些过去必须由高性能计算集群或超级计算机处理的计算任务可被转换到单个小型计算机上进行，大大降低了硬件成本和运行成本。已有研究成果表明，基于CUDA架构的并行算法可在AMT正反演加速中发挥出色的作用[20-21]。

为此，在CUDA 架构下开展带地形AMT数据的二维反演并行算法研究，旨在利用GPU强大的计算能力及并行计算技术实现高精度、快速度的AMT数据二维反演，并为后续开展并行三维反演建立基础。

1 AMT二维正演与反演

1.1 AMT二维有限元正演模拟

对于一般二维各向同性介质，若取坐标系x轴方向为地质体走向(即电性沿此方向不变)，z轴垂直向下，则与之对应的二维MT边界值问题的变分问题[22]为

(1)

TE和TM两种模式的边界条件基本一致，仅在上边界AB位置的选择上有所不同。对于TE模式，上边界位于空气中，并离地表足够远，对于TM模式上边界则位于地表。

为适应地形变化，本研究使用双线性任意四边形单元对区域Ω进行剖分。将求解区域剖分为多个四边形单元，在离散的每个单元上进行线性化处理，最后合成总体系数矩阵为

(2)

式(2)中：K=K1e+K2e+K3e为有限元总体系数矩阵。令式(2)的变分值为零，得线性方程组为

Ku=0

(3)

代入顶边界条件u|AB=1.0，当求解TE模式时AB位于空气中顶边界，当求解TM模式时AB位于地表。由于方程中的矩阵K是稀疏对称正定的，为了节约内存空间按变带宽存储，本文中采用稀疏矩阵快速回代的Cholesky分解法求解方程。

1.2 ARIA二维反演

自适应正则化反演方法(adaptive regularized inversion algorithm ,ARIA)是陈小斌等[23]提出的一种反演方法，相较于传统的Occam算法，ARIA采用简单有效的正则化因子求取算法，其收敛时间更快，拟合效果基本相同。其总目标函数可归结为

Φ=Φd+λΦm→min

(4)

式(4)中：Φd=[d-A(m)]TWd[d-A(m)]为数据目标函数；Φm=mTCxm+mTCzm为模型目标函数；λ为数据目标函数和模型粗糙度的正则化调节因子，即

Φ=[d-A(m)]TWd[d-A(m)]+

λ[mTCxm+mTCzm]

(5)

根据目标函数极小化原则，可得反演矩阵方程为

WdJΔm+λ(Cx+Cz)Δm=WdΔd-

λ(Cx+Cz)m

(6)

式(6)中：J为正演数据对模型的偏导数矩阵。

这样每次迭代模型的更新为mi+1=mi+Δm。

为保证反演过程中数据目标函数值不受数据误差的影响，对数据方差进行了规范化处理，使得正则化因子的取值与数据误差的大小基本无关，即

(7)

(8)

反演中每一步计算都需要极小化正则化因子，此过程需要重复的正则化求解反演方程组，较为耗时，为了减少计算量本文根据数据目标函数和模型目标函数的关系进行自适应正则化因子调节[23]，关系式为

(9)

2 CUDA架构下AMT二维正反演并行计算实现策略

AMT正反演中涉及多个频率、多个测点和大量网格计算单元。传统串行算法是将每个频点、每个测点、每个网格单元依次计算，当测点、频点、网格单元较多时势必涉及巨大计算量，造成计算速度慢。如果将多个测点、频点、网格单元的计算分成多个模块的线程来进行独立执行，这样就可以提高计算速度，从而缩短计算时间，这便是并行计算的主要思想。

在AMT二维反演计算中，灵敏度的计算、反演矩阵方程组的正则化求解、模型响应部分为主要的耗时计算部分，因此是需要并行的部分。其中AMT灵敏度的计算和模型的响应部分都需要对多个频率进行单独计算，且各频率对应的电磁场值间是相互独立的；反演矩阵方程组的正则化求解过程中需要对矩阵A(M×N)进行正则化得到矩阵B(M×N)，且这个正则化的过程中矩阵B每个元素的计算是相互独立的，根据这些特点可以将程序按频率或者矩阵的行数和列数进行分粒度，将每个频点或矩阵的每数元素分配到各个进程同时进行计算，并行执行。

二维反演计算中模型灵敏度矩阵的计算、反演方程的正则化处理以及求解部分主要的耗时计算部分，因此同样的将其定为需要并行的部分。在AMT二维反演灵敏度矩阵计算中，各个测点及各个模型所涉及的计算都是相互独立的；反演方程的正则计算中，正则化后的每个元素计算都是相互独立的；正则化后的矩阵方程进行不完全三角分解的预条件共轭梯度法(incomplete cholesky factorization preconditioned conjugate gradient，ICCG)求解迭代时将涉及到大量的矩阵、向量的乘积计算，也是可以采取并行计算加速的。因此在二维反演灵敏度矩阵计算中将程序按测点、纵向网格分块数量、横向网格分块数量进行粒度分布，将各个测点针对各个有限单元网格的偏导数计算进程同时进行，并行执行；在反演方程的正则计算中，将程序按模型数量分成多个线程块，在同一个线程块中又将其分成多个线程；在正则化后的矩阵方程进行ICCG求解迭代时每一步的矩阵与向量的乘积计算使用并行化处理。

本文中程序实现的过程使用的是主从并行模式，即将程序的执行分主函数进程和子函数进程，主进函数程控制全局的数据结构，主要负责子进程任务数量的划分、派发、结果回收及输出结果；子函数进程主要负责执行由主进程分发指定的任务并把结果回传给主函数进程。其中正演计算部分具体的实现过程是：主进程读入网格剖分数据及网格单元电阻率值，并将其传送给子进程，按频率划分给子进程各自计算模型的响应，并将计算结果传给主进程，主进程整合所有计算的结果，并将其输出；反演灵敏度计算部分具体的实现过程是：主进程读入正演所需的数据及模型数据，并将其传送给子进程，按测点数进行划分子进程各自计算测点位置的电磁场值关于模型偏导数，以及按测点数和有限元模型单元数进行划分子进程各自计算测点响应关于模型单元的偏导数，并将计算结果传给主进程，主进程整合所有计算的结果，并将其输出。图1所示为二维正演并行计算简化流程图，图2所示为二维反演模型灵敏度计算并行计算简化流程图。在并行计算中，CUDA并行计算需要CPU来对GPU分配计算线程，由GPU来执行计算，最终再将计算结果返回CPU。GPU作为设备来完成设备(Device)代码命令部分，这部分代码中CPU分配的进程与GPU的计算众核对应位置关系是随机的，并且独立完成，CPU作为主机(Host)对GPU下达线程分配命令，并等待GPU计算返回结果。

图1 AMT二维正演CPU+GPU并行计算流程图

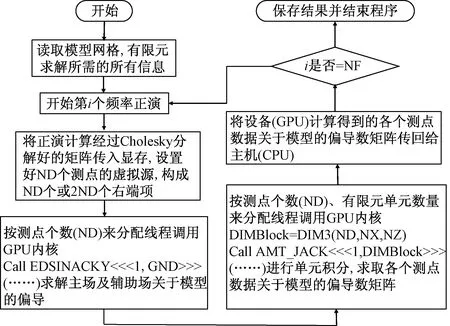
图2 基于CPU+GPU的偏导数矩阵并行计算流程图

3 程序准确性验证

3.1 一维层状模型

为了验证程序算法的正确性，首先设计了一个8层一维模型，各层电阻率ρ和厚度h分别为ρ=[10、200、20、100、2、500、50、10] Ω·m，h=[100、500、200、1 000、1 000、5 200、10 000] m。正演计算频率为55个，最高频率为100 000 Hz，最低频率为0.000 01 Hz，每个数量级按6个频点对数等间隔取值。将正演结果(电阻率和相位)与一维解析解进行对比, 如图3所示。结果表明，该二维正演程序所获结果与一维解析结果基本完全拟合，验证了该算法及程序是可行的且是准确的。

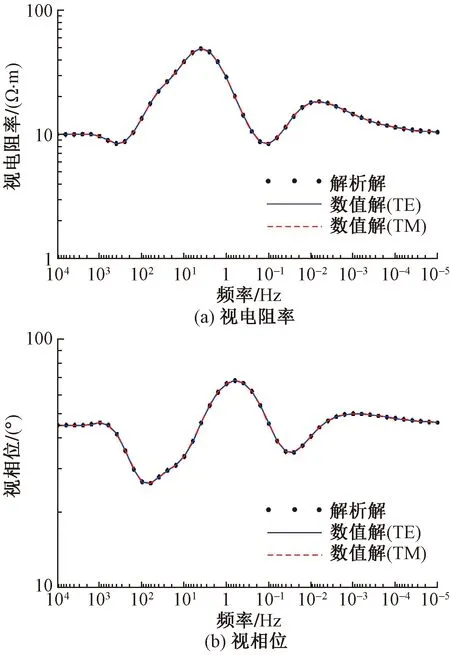
图3 8层模型二维正演计算结果与解析结果对比

然后利用本文所提出的反演方法对上述二维正演结果进行一维、二维反演，结果如图4所示。由反演结果可以看出，一维、二维反演结果基本一致，都能较好地将数据恢复到真实模型附近。说明一维反演算法是可靠的，基于CUDA并行计算的二维反演也是正确的。

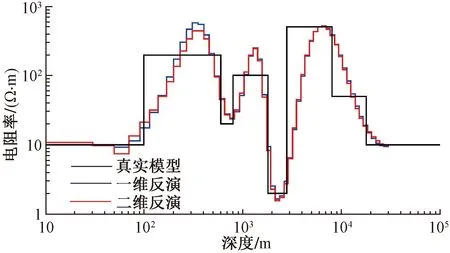
图4 8层模型1D和2D反演结果对比图

3.2 二维模型

接下来，通过三个复杂程度依次递增的二维模型验证本程序的准确性，结果如图5～图7所示。可以看出，本文算法对于单独TE反演时对低阻体的形态恢复较好，单独TM反演时对高阻体的形态恢复较好，这与AMT中TE、TM两种模式对高低阻体反应灵敏度特性有关。但总体来说无论是对于不带地形的简单二维模型(图5)，还是带地形的二维简单(图6)和较复杂模型(图7)，本文算法都能很好地复原模型的真实结构，特别是当采用TE+TM模式反演时，反演结果对模型中的高、低阻异常的形态和位置都做出了准确地刻画。由此可说明，该程序在处理二维模型的正反演中具有较高的精度。

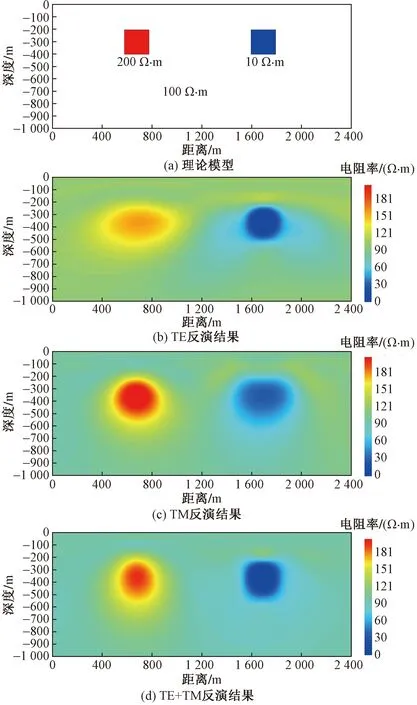
图5 简单二维模型反演结果

图6 带地形的简单二维模型反演结果

图7 带地形的复杂二维模型反演结果

4 并行加速及压缩效果对比

为了说明CDUA并行计算方法在正演计算速度上的优越性，与基于CPU串行计算的有限单元法计算程序进行了对比，同时测试了5种不同网格剖分在GPU硬件环境下的执行效率(硬件环境为Intel© core(TM) i7-9750 CPU 2.60GHz及NvidiaGeForce GTX1660 Ti)，测试结果如表1、表2所示。从表中可以看出无论在何种测点、频率、网格配置下，GPU计算速度都要比CPU的计算速度快，且计算网格越大加速比越高，加度比计算公式为

表1 灵敏度矩阵串行与并行计算效率对比

表2 矩阵正则化非压缩串行与压缩并行计算效率对比

(10)

由此可以说明本文所提的并行反演方法可行，在同样的测点、频点、模型网格情况下可以更快地得到反演结果，在实际应用中就能提高效率，从而可以开展更多测点的长剖面测量工作。

5 应用实例

上述数值模拟结果表明，采用本文提出的并行计算方案，可以极大地提升AMT数据的二维反演效率。最后，以云南某金属矿的AMT探测数据反演为例，说明本文提出的二维反演方法在实际应用中的效果。如图8所示，测量区位于云南永平某铜钴多金属矿区，区内发育的褶皱主要为向斜，局部发育一些小型褶皱。向斜紧靠F4矿化带西侧展布，轴向30°，轴部地层为花开左组下段(J2h1)，两翼为漾江组(J1y)及麦初箐组上段(T3m2)，西翼被F4断层所切，出现J2h1与T3m2接触，并出现强烈蚀变及铜矿化。矿段内矿体主要赋存于向斜西翼三叠系与侏罗系过渡部位，主要受F5号带控制，分布于矿段中部，为一组平行断裂带。断裂带产状：260°～330°∠40°～65°，倾角呈现南陡北缓的特征，北侧向西转折，走向为北西，切过侏罗纪和三叠纪地层。断裂带的成分主要为蚀变碎裂岩，铜矿化普遍发育，主要铜矿物有砷黝铜矿、黄铜矿、斑铜矿、辉铜矿、孔雀石、铜蓝等。

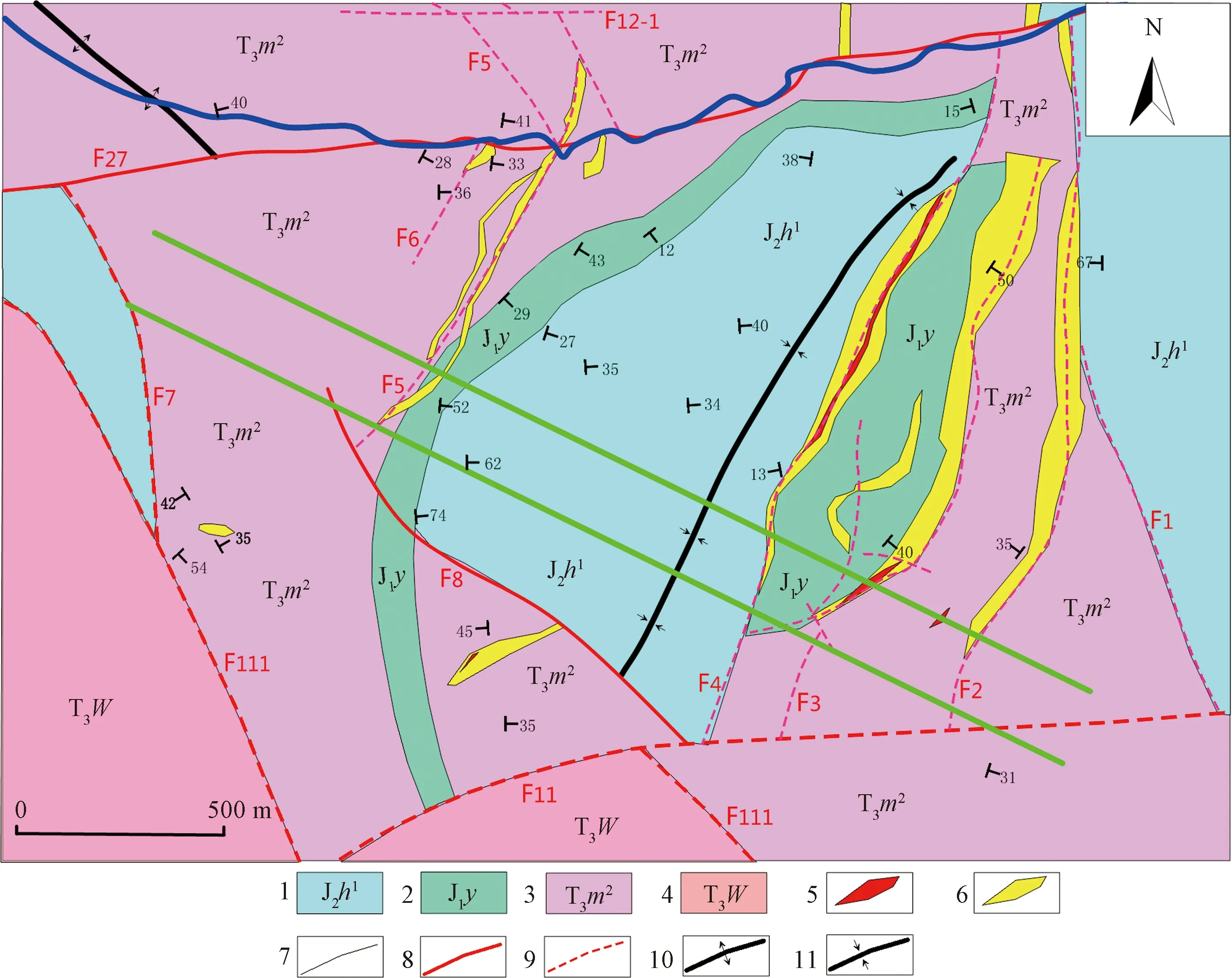
1为侏罗系中统;2为侏罗系下统;3为三叠系;4为三叠系;5为出露工业矿体;6为出露低品位矿体;7为地质界线;8为实测断层;9为推测断层;10为背斜;11为向斜

为获得目前正在开采的F5号带所控制矿体南沿以及F2、F3、F4号带的深部形态，对矿山南沿的矿产资源潜力做出初步评价，在测区实施了AMT测量。共布置2条AMT测线，点距20 m，观测频率为1.0～32 000 Hz，每数量级10频点对数等间隔分布，TM标量测量，使用仪器为重庆地质仪器厂生产的CLEM阵列电磁法系统。

以L01线数据为例进行并行二维反演，并对反演结果进行地质资料解释与验证。L01线长度为2 400 m，共包含121个TM标量测量点。反演初始模型设置横向129块，每块20 m，顶层厚度10 m，往深部按1.1倍逐步增加，共34层。设置好参数之后，程序根据具体测点的实际坐标分布适当地自动调节横向宽度，使得测点尽量落在模型块的横向中心位置；纵向模型位置分布根据地形起伏自动贴合，一方面适应地形起伏，另一方面使得模型往深部逐步变平缓。初始模型电阻率设置为100 Ω·m，设置好反演参数之后进行自动迭代反演。在Win10 64位，i7-9750H CPU 2.60 GHz，NVIDIA GeForce GTX1660 GPU配置上运行，迭代15次，拟合残差3.37%，用时约30 min，结果如图9所示。

由图9可以看出，受断裂带影响测区地层的电性结构较为错乱，浅层地表电性特征与地质揭露的实际资料基本相符，在F5号带附近实施的钻孔所揭示的中浅部地层结构也能与本结果相对应。测线中部和南部出现的两处大面积的低阻异常区域是F3和F4号断裂带的反映，它们在水平位置上能够与实际情况相吻合，并显示出向深部继续延伸的趋势。该二维反演结果很好地刻画了地下电性结构的形态，表明本文提出的并行二维反演算法具有较高的反演精度，且具有可观的计算效率，在实测数据的反演处理中可以获得很好的效果。

图9 L01线二维反演高程-电阻率断面图

6 结论

正演、灵敏度矩阵计算、反演方程组正则化是影响MT数据二维反演效率的主要部分，而它们具有很好的并行性，因此利用GPU强大的计算能力及并行计算技术可极大地提高AMT二维反演程序的运行效率。在CUDA 架构下实现了基于有限元和自适应正则化反演算法的带地形AMT数据的二维反演并行计算，并通过理论模型验证了方法的有效性和准确性。数值模拟结果表明，该并行算法可显著提升灵敏度矩阵计算和反演方程组正则化求解的效率，最高加速比可达10倍以上。通过对数值模拟结果以及野外实测数据的处理表明，本文所提出的AMT二维并行反演方法在保证高精度的前提下具有很高的计算效率，可为今后研究及实际生产应用提供一种有力工具。