带切角桁架钢筋叠合板的吊点位置多目标优化及结果应用研究

翁 柳 青

黎明职业大学 土木建筑工程学院,福建 泉州 362000

我国装配式混凝土结构中桁架钢筋叠合板应用最为广泛的受力构件,有效提高结构的装配率,但受限于现浇层厚度要求,预制底板的刚度不足[1],在生产脱模、吊装过程中容易出现混凝土开裂,在没有桁架筋的截面开裂更为普遍[2].姚一辰等[3]人通过有限元模型分析得出叠合板在脱模、吊装时的受力性能影响因素为悬挑长度、板宽、吊绳等.国家建筑标准设计图集(15G366-1)《桁架钢筋混凝土叠合板》[4]给出关于部分叠合板的起吊悬挑长度、吊点数量及位置的建议.邹贻权等[5]人认为叠合板在生产及施工过程中混凝土开裂的主要影响因素为吊点设计错误或起吊时遗漏,吊点数量或位置设计不合理,则会增加混凝土剥落及开裂的风险.其根据叠合板起吊计算模型分析得出四、六点起吊情况下叠合板的最优力学吊点.以上研究对于规则桁架钢筋叠合板的受力性能进行分析,给出吊点位置建议,但未涉及异形的桁架钢筋叠合板.

随着装配式建筑的多样化发展,往往需拆分异形的叠合板以适应当地装配率的要求[6].在实际工程中,叠合板因与墙柱碰撞、预留洞口、拆分前本为异形板而设置切角,导致力学最优吊点发生改变.因此,带切角的桁架钢筋叠合板的吊点位置优化需要进一步研究.郁文海等[7]人认为叠合板的吊点位置优化应充分利用混凝土自身的抗拉性能,使叠合板的正负弯矩绝对值最相近.带切角的叠合板往往四、六点起吊,弯矩图上存在多个弯矩极值,导致吊点的位置优化涉及多目标优化.此外,叠合板起吊时截面上的多个弯矩极值随吊点的位置变化呈非线性变化[5],并存在此消彼长的冲突关系.粒子群算法因参数少、易实现的特点,被广泛应用于多目标优化[8],但无法同时优化具有冲突性的多目标最优解[9],而改进的多目标粒子群优化算法优化性能得到改善,但相关的数学理论仍不够完备[10].传统的多目标优化算法如加权求和法、约束法、目标规划法[11]等理论较为完善,具有确定的优化终止准则,但当目标函数为非线性时,优化效果并不理想[10].因此,如何基于一种数学理论完备且适合、简易的多目标优化算法共性分析不同切角比例下叠合板的吊点优化布置规律值得研究.由此,将建立带切角的桁架钢筋叠合板的起吊计算模型,结合力学分析得出多弯矩极值关联吊点位置的表达式.根据已有的研究初步估计吊点的优化范围,并构建吊点位置搜索矩阵,基于Matlab矩阵运算[12]的“点乘”功能计算得出多弯矩极值矩阵,以多弯矩极值矩阵同位元素最大值最小判定吊点处于最优位置,从而将多目标优化问题转化为单目标优化问题.再以叠合板切角在叠合板长跨向的尺寸与叠合板长度的比值为变量,共性分析不同切角比例下桁架钢筋叠合板力学上最优吊点的共性布置规律,并做出优化前后的比较，最后,通过算例分析优化理论结果的应用.

1 带切角叠合板的起吊计算模型

1.1 吊点与切角的位置关系

在实际的装配式混凝土结构中,带切角的桁架钢筋叠合板多数为一角设置切角如图1所示.其中,l1为切角在叠合板长跨向的尺寸,l2为切角在叠合板短跨向的尺寸.《装配式混凝土结构技术规程》(JGJ1-2014)6.6.7条[13]规定桁架钢筋距离板边不应大于300 mm.因此,当l2大于300 mm时,外排的桁架钢筋与切角处于同一板带(图1阴影部分).而在实际工程,为避免设置吊环而将吊点设置于桁架钢筋的波峰处如图1所示,即叠合板的其中一排吊点与切角处于同一板带.

图1 带切角的桁架钢筋叠合板(左上角设置切角、四点起吊)Fig.1 Truss steel reinforced composite slab(with a cut corner on the upper left,four-point hoisted)

1.2 简化的起吊计算模型

叠合板对称起吊时,若对称吊绳与叠合板的夹角相等,起吊绳的水平分力互相平衡[14],则叠合板受力计算简图为承受均布线荷载的外伸梁[5,7].因受限于运输,叠合板设计宽度与长度相比较小,即叠合板短跨向板带计算跨度相比长跨向的小,且若将吊点设置于桁架钢筋上,吊点的位置取决于桁架钢筋的位置及间距;若在吊点设置吊环,则叠合板短跨向内力较易于控制,因此将重点分析叠合板切角尺寸l1对长跨向吊点优化设置的影响.

图1中带切角的桁架钢筋叠合板四点起吊下长跨板带的受力计算简图与弯矩图如图2所示.同理,跨度较大的叠合板六点起吊下长跨板带的计算简图与弯矩图如图3所示.

其中,a为切角在叠合板长跨向的尺寸与叠合板长度的比(l1/L),q为计算板带所承受的线荷载,x1、x2分别为叠合板四点起吊下长跨板带两侧悬挑长度与叠合板长度的比,x3、x4分别为叠合板六点起吊下长跨板带两侧悬挑长度与叠合板长度的比,x5、x6均为叠合板六点起吊下长跨板带计算跨度与叠合板长度的比.图2(b)与图3(b)中的M1～M16为对应吊点和板跨中的弯矩极值.因对称起吊,M2=M4,M8=M10.此外,因叠合板的一角设置了切角,导致相邻跨跨中弯矩最大值增加,即M6>M5,M14>M13.因此,为使得M1～M6、M7～M16均相对较小,将基于多目标优化共性分析不同切角比例(a=l1/L)下叠合板四、六点起吊的吊点最优位置.

(b) 长跨板带图2 四点起吊下的计算简图与弯矩图(左侧设置切角)Fig.2 Calculation diagram and bending moment diagram under four-point hoisted(with a cut corner on the left)

(b) 长跨板带图3 六点起吊下的计算简图与弯矩图(左侧设置切角)Fig.3 Calculation diagram and bending moment diagram under six-point hoisted(with a cut corner on the left)

2 带切角叠合板的吊点位置多目标优化

2.1 构建吊点位置搜索矩阵

(a) 切角范围内长跨板带

(a) 切角范围内长跨板带

(1)

X2=X1T

(2)

六点起吊情况下,x3～x6的搜索矩阵X3,X4,X5,X6均为三维矩阵,行列及平面数均为n+1,见式(3)～式(6)

(3)

X4(:,:,k)=X3(:,:,k)Tk=1，…，n+1

(4)

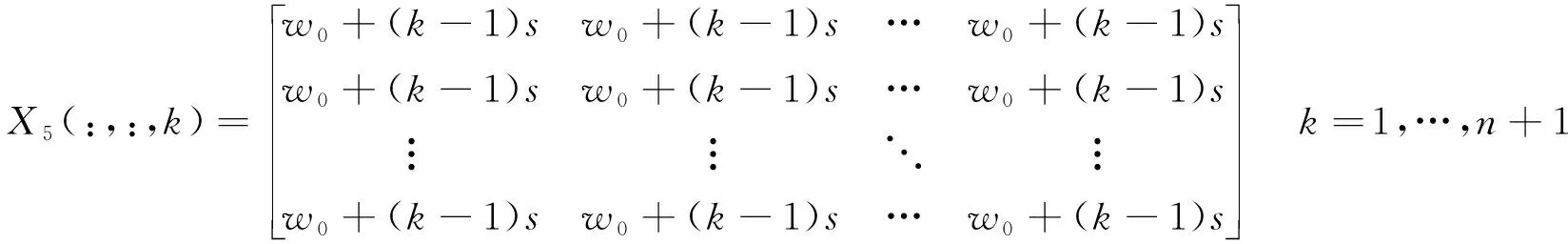
(5)

X6=E-X3-X4-X5

(6)

其中,X3(:,:,k),X4(:,:,k),X5(:,:,k)分别表示三维矩阵X3,X4,X5空间上第k平面的二维矩阵;E表示与X3～X5同型的三维矩阵且元素数值均是1.

2.2 计算弯矩极值矩阵

利用Matlab矩阵运算的“点乘”功能,根据X1～X6计算得出图2(b)和图3(b)中的弯矩极值所形成的矩阵M1～M16.四点起吊情况下,M1～M6为二维矩阵见式(7)～式(11)

M1ij=0.5X1ij2qL2

(7)

M4ij=M2ij=0.5X2ij2qL2

(8)

M3ij=0.5(X1ij-a)2qL2

(9)

(10)

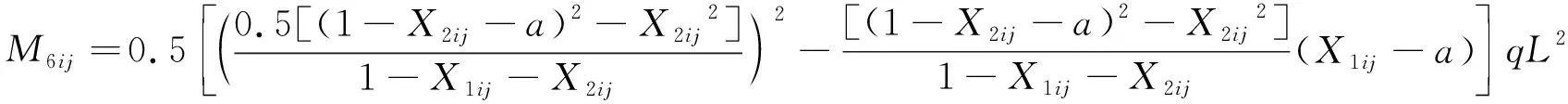
(11)

其中,下标“ij”表示矩阵的第i行与第j列,i=1,…,n+1,j=1,…,n+1.

六点起吊情况下,M7～M16为三维矩阵,通过图乘法及力法分析超静定外伸梁可求.图3(a)中的支座反力矩阵与弯矩极值M7～M16矩阵的表达为式(12)～式(24)

(12)

(13)

R4aijk=

(14)

(15)

M7ijk=0.5X3ijk2qL2

(16)

(17)

(18)

M11ijk=0.5(X4ijk+X6ijk)2qL2-R4ijkX6ijkL

(19)

M12ijk=0.5(X4ijk+X6ijk)2qL2-R4aijkX6ijkL

(20)

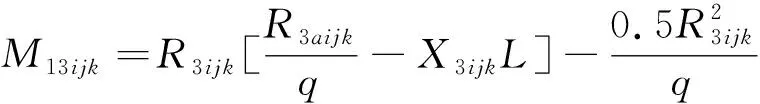
(21)

(22)

(23)

(24)

其中,下标“ijk”表示矩阵的第i行第j列第k平面处,i=1,…,n+1,j=1,…,n+1,k=1,…,n+1.

2.3 弯矩极值矩阵同位元素最大值最小定位

比较弯矩极值矩阵对应空间位置数值,以最大值组建新矩阵ZM4(四点吊)、ZM6(六点吊)见式(25)和式(26)

ZM4ij=max(M1ijM2ijM3ijM5ijM6ij)i=1,…,n+1j=1,…,n+1

(25)

ZM6ijk=max(M7ijkM8ijkM9ijkM11ijkM12ijkM13ijkM14ijkM15ijkM16ijk)

i=1,…,n+1j=1,…,n+1k=1,…,n+1

(26)

之后,分别得出ZM4和ZM6中元素最小值的位置,如图4所示,再推出X1～X5矩阵中对应位置的元素值,即为x1～x5的值,由此得出叠合板力学上最优吊点的位置.

图4 矩阵元素值三维图Fig.4 Three-dimensional image of matrix element values

2.4 吊点位置多目标优化算法的流程

带切角的桁架钢筋叠合板的吊点位置多目标优化算法的流程如图5所示.

图5 吊点位置多目标优化算法的流程Fig.5 Flow of multi-objective optimization algorithmfor hanging points’ position

2.5 吊点位置多目标优化理论结果

2.5.1 四点起吊

四点起吊情况下,因未设切角的叠合板的最优力学吊点在0.207L处[5],所以设切角在叠合板长跨向尺寸与叠合板长度的比值a=0～20 %.基于以上优化算法,带切角的桁架钢筋叠合板的吊点位置优化结果及优化前后最大弯矩比较见表1.

表1 四点起吊下吊点位置优化结果及优化前后最大弯矩比较Table 1 Optimization results of hanging points’ position and comparison of the maximum bending momentbefore and after optimization under four-point hoisted

结果显示,当a=0,也就是叠合板不设切角时,x1和x2的力学标准值为0.207,与文献[5]吻合,说明优化算法及Matlab编程有效.随着a的增加,x1和x2逐渐增加,即叠合板起吊时两侧悬挑长度逐渐增加如表1所示,最优力学吊点逐渐向内移,但移动的幅度逐渐变缓如图6(a)所示.其中,去除多目标优化个别非劣解后,x1和x2保持数值一致见表1,不仅能均衡多吊点及跨中的弯矩极值,且便于设计和施工.此外,随着a的增加,吊点位置优化前后叠合板的最大弯矩均逐步增加,说明切角尺寸增大对叠合板起吊的不利影响增加.而吊点位置优化后,叠合板的最大弯矩增幅较小如图6(b)所示,说明吊点位置优化能够有效降低带切角的叠合板起吊时的最大弯矩.例如当a=10 %时,优化后最大弯矩Mmax比优化前小18.5 %见表1.

(a) 优化前后x1,x2的对比

(b) 优化前后最大弯矩对比

2.5.2 六点起吊

六点起吊情况下,因未设切角的叠合板外侧4个吊点的最优力学位置在0.145 L处[5],所以设切角在叠合板长跨向尺寸与叠合板长度的比值a=0～14 %.基于以上优化算法,带切角的桁架钢筋叠合板的吊点位置优化结果及优化前后最大弯矩比较见表2.

表2 六点起吊下吊点位置优化结果及优化前后最大弯矩比较Table 2 Optimization results of hanging points’ position and comparison of the maximum bending momentbefore and after optimization under six-point hoisted

结果显示,当a=0,也就是叠合板不设置切角时,x1,x2,x3,x4的力学上标准值分别为0.145,0.145,0.355和0.355,与文献[5]吻合,说明优化算法及Matlab编程有效.随着a的增加,同四点起吊,x3和x4的值同步逐渐增加如表2及图7(a)所示,即外侧的4个吊点逐渐内移,但幅度逐渐变缓如图7(a)所示.而x3与x4的值并不完全相等,但大小较为相近见表2.此外,随着a的增加,吊点位置优化前和优化后叠合板的最大弯矩均逐步增加,但优化后比优化前的小如图7(b)所示,说明吊点位置优化能够降低叠合板起吊时的最大弯矩.例如当a=10 %时,优化后最大弯矩Mmax比优化前小8.8 %见表2.相比四点起吊,六点起吊下吊点位置优化后最大弯矩降低百分比相对较小.

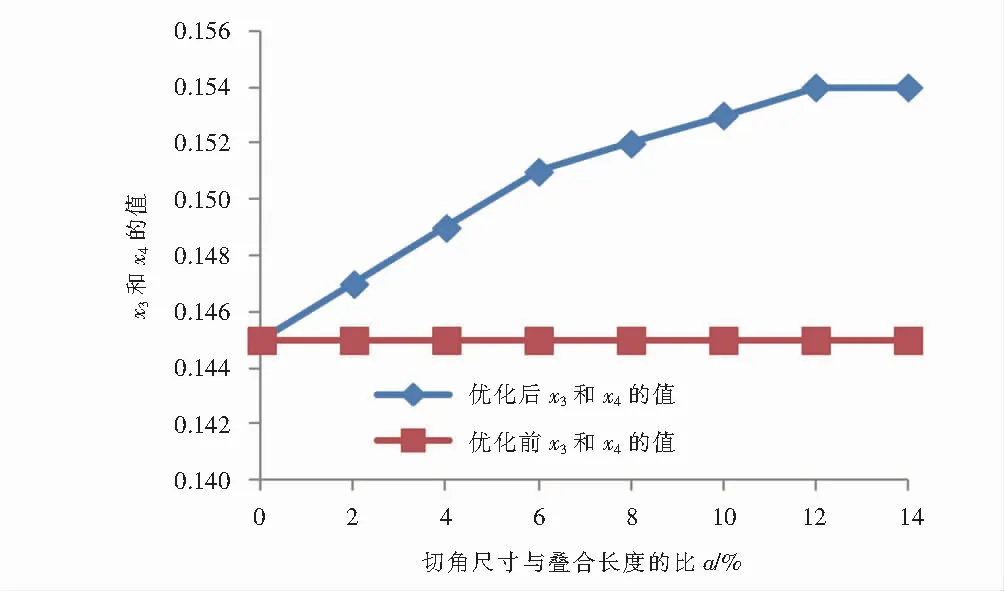
(a) 优化前后x3和x4的对比

(b) 优化前后最大弯矩对比

3 带切角叠合板的吊点位置优化理论结果应用

3.1 考虑桁架钢筋的节点间距

由于桁架钢筋叠合板的吊点往往设置于桁架钢筋的波峰处,导致吊点的位置一定程度上受限于桁架钢筋的节点间距如图8所示.

图8 桁架钢筋叠合板的立面图Fig.8 Elevation image of truss reinforced composite slab

目前工程上常用的桁架钢筋为定型桁架钢筋.根据中华人民共和国黑色冶金行业标准《钢筋混凝土用钢筋桁架》YB/T4262-2011第6.3条[15],定型桁架钢筋的节点间距优选200 mm.由此说明,桁架钢筋叠合板的总跨度通常是200 mm的整数倍,叠合板起吊时两侧的悬挑长度再依此确定.

3.2 数值算例

以15G366-1图集中的桁架钢筋叠合板为例,设其一角带切角(a=10 %),根据以上吊点位置优化理论结果重新设计其吊点的位置.表1和表2显示,四点、六点起吊下外侧4个吊点的力学标准位置在0.220L及0.153L处.桁架钢筋叠合板的深化设计时,因需确保叠合板起吊时的总跨度是200 mm的整数倍,导致无法完全将吊点设于力学标准点上,但能以此作为参考优化吊点的位置.若叠合板长为L,四点起吊时,叠合板的总跨度应与(1-0.220)L接近且为200 mm的整数倍;六点起吊时,叠合板的总跨度应与(1-0.153)L接近且为200 mm的整数倍.叠合板起吊时的总跨度确定后再依此确定起吊悬挑长度.根据以上方法,15G366-1图集中叠合板(设一角带切角,a=10 %)的吊点位置优化后的信息见表3.

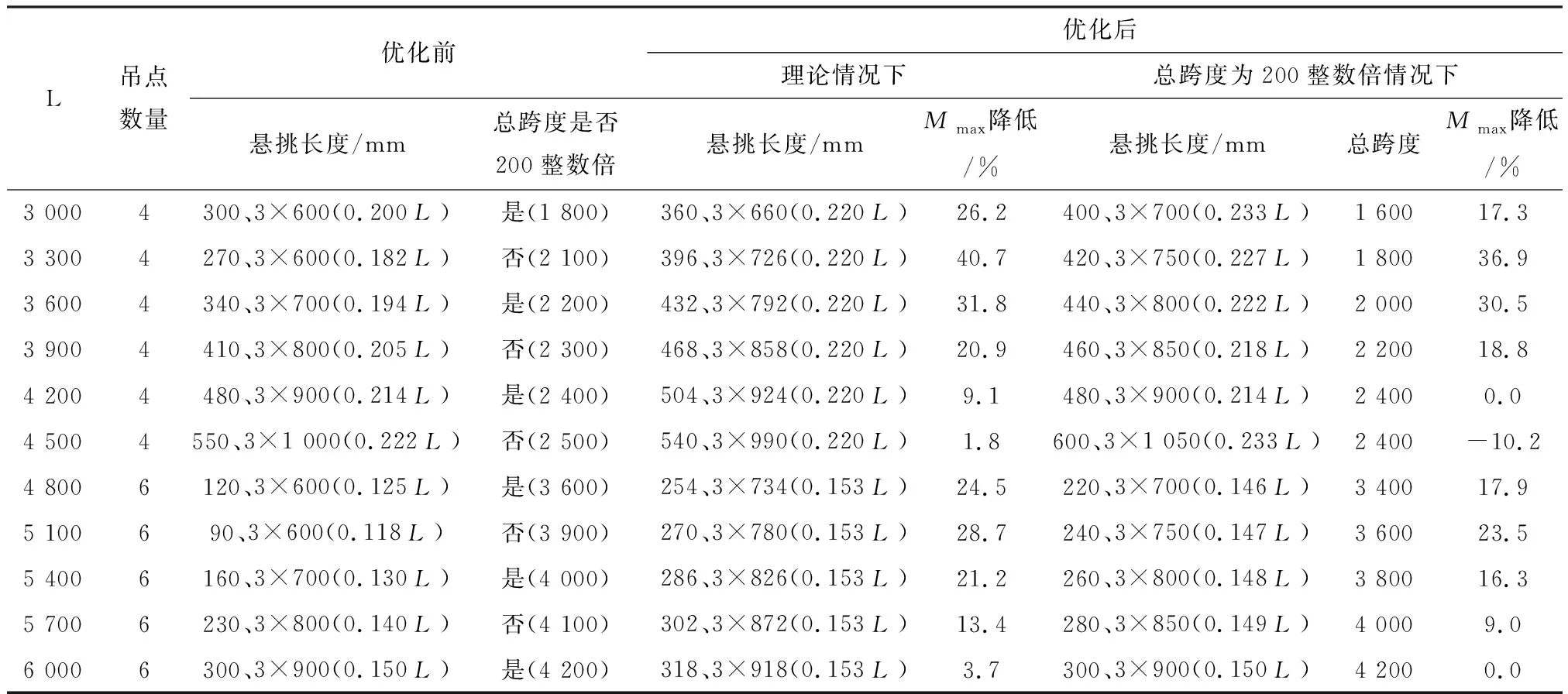
表3 15G366-1图集中叠合板的吊点位置优化前后信息对比(设一角带切角,a=10 %)Table 3 Comparison of information about truss reinforced concrete composite slabs on the 15G366-1 atlas before andafter optimization of the hoisting points' position (with a cut corner,a=10 %)

结果显示,叠合板的吊点位置优化后,起吊时截面最大弯矩Mmax均降低.理论优化情况下,起吊时截面最大弯矩降低1.8 %～40.7 %,优化效果明显,但仅适用于采用定制桁架钢筋或设置吊环的情况.而参考理论优化结果并限定总跨度为200 mm整数倍情况下,截面最大弯矩降低0～36.9 %,相比理论优化,效果稍不如,但一定程度上说明吊点位置优化理论结果的应用可行.其中,长为4 500 mm的叠合板吊点位置优化后(总跨度为200整数倍情况下),起吊时截面最大弯矩反而增加10.2 %,是将叠合板起吊的总跨度设为常用节点间距200 mm的整数倍导致的,属正常.

4 结论

(1) 通过二维、三维矩阵的构建与运算便于比较相同情况下多个目标函数(弯矩)的大小,以其最大值最小为条件有效判定最优工况,所提优化算法有效.但随着矩阵行列数的增加,在一定程度上影响计算时间.

(2) 叠合板及其切角的尺寸多样,以切角在叠合板长跨向的尺寸与叠合板长度的比值为变量便于共性分析带切角的桁架钢筋叠合板的吊点优化布置规律,为叠合板的深化设计提供参考.

(3) 四、六点起吊情况下,随着切角尺寸的增加,外侧四个吊点的力学最优位置逐渐同步内移,吊点位置优化后叠合板截面上的最大弯矩均一定程度上降低.

(4) 在确保起吊时总跨度为桁架钢筋节点间距整数倍的情况下,参考优化后的理论结果设定吊点的位置,能够有效降低叠合板起吊时截面上的最大弯矩,降低叠合板在加工及装配环节开裂的风险.

(5) 若为达到较优的吊点位置理论优化效果,可选用定制桁架钢筋或设置吊环,以便将吊点设于力学标准点上,较大程度降低叠合板起吊时截面上的最大弯矩,但一定程度上影响叠合板的生产效率.

(6) 此外,四、六起吊情况下,若叠合板的一角切角尺寸与叠合板长度的比不小于22 %和16 %,外侧吊点的力学最优位置在靠近切角的桁架钢筋波峰处,吊点对称设置.但若叠合板的切角尺寸较大,叠合板的异形程度大,吊点的位置优化应视具体情况而定,有待于进一步研究.