基于GA-BP神经网络的砌体结构拆除造价预测
王 勃,杨占秋,董丽欣
吉林建筑大学 土木工程学院,长春 130118
0 引言
随着我国经济的快速发展,新建建筑物趋于平稳发展,而待拆除建筑物日益增多,且多为上世纪的砌体结构建筑物.在砌体结构建筑物拆除工程中,造价是施工方案决策中的主要控制指标之一.造价的快速精准的估测对于拆除工程的招投标具有重要意义.近些年,有专家学者将一些智能算法应用至建筑工程领域进行数据分析,他们多数采用1986年 D.E.Rumelhart及其研究小组提出的误差反向传播(BP)算法,此方法已成为至今影响最大、引用最广的一种神经网络[1],其具有良好的自学习、自适应、鲁棒性[2]和泛化能力.但BP算法存在收敛速度慢且很容易陷入局部极小值等缺点.为解决这一问题,本文将遗传算法与BP神经网络结合起来,优化BP神经网络的权值和阈值,进而提高砌体结构拆除阶段造价的精度及稳定性.
1 BP神经网络算法
BP(Back propagation,BP)[3]是人工神经网络研究最多、应用最广泛的一种算法,具有至少三层的神经网络,包括导入数据层、隐含层、输出结果层,其中隐含层至少有一层,也可以有多层前后两层各节点全连接,其结构如图1所示[4].
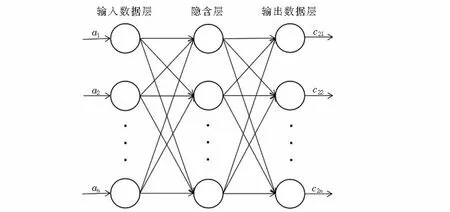
图1 BP神经网络的连接结构Fig.1 The Connection structure of BP neural network
BP神经网络算法学习过程是一种信息正向传播和误差反向传播的学习方式.前向传播时,数据通过输入数据层输入进来再通过隐含层进行数据处理,最终传给输出数据层,将输出结果与期望结果对比,若不满足要求则进行误差的反向传播,调节各连接层的权值阈值,使得误差满足期望.由于BP神经网络算法采用的是一种梯度下降法,所以存在一些缺陷,例如:学习速率过慢,容易陷入极值,网络拓扑结构难以确定等.
2 遗传算法(GA)
遗传算法(Genetic algorithm,GA)[5-6]于20世纪70年代由美国John Holland提出.遗传算法仿照生物进化论理论,具有在自然环境中适者生存,优胜劣汰的生物特点,在遗传和进化过程而形成的一种自适应全局优化搜索算法.它模拟了生物的选择、交配和变异现象,能够自适应学习最优解,具有良好的全局搜索能力和鲁棒性,适合复杂的非线性求解问题.本文使用遗传算法优化BP神经网络,主要是对BP神经网络的权值阈值进行调节,充分发挥遗传算法和BP神经网络各自的优点,弥补其缺点,使输出结果更加稳定,并符合研究问题的合理期望.
3 遗传算法优化BP神经主要流程
3.1 遗传算法优化部分
第1步:运用实数编码,对BP神经网络的权值和阈值进行初始化,得到初始化数据种群.
第2步:将期望输出值与真实输出数据的误差绝对值作为适应度函数变量值Z,适应度函数计算公式为:
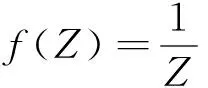
(1)
第3步:经过选择、交叉、变异运行操作,形成新的个体,对比检查其是否满足要求,若不满足则返回第二步;若符合,则将其权值和阈值输出赋予给BP神经网络[7].
3.2 BP神经网络部分
第1步:确定网络拓扑结构(BP神经网络的导入数据层、隐含层、输出结果层的各个经神元个数).
第2步:导入训练数据,划分训练集、测试集,由于各个输入参数量不同所以需要将数据进行归一化处理,映射到[-1,1]范围之间.
第3步:运用经过遗传算法优化过后的权值和阈值对BP神经网络进行向前传播训练.假设误差用R代表期望输出值M与预测输出值N差的绝对值[8],如式(2):
Ri=|Mi-Ni|
(2)
假定许可最大误差值为R0,当maxRi≥R0代表未达到精度期望,则反向传播继续训练,直到满足误差标准或者达到训练迭代次数才终止训练.
第4步:输出预测砌体结构拆除造价结果[9-11].
4 GA-BP砌体结构拆除造价模型建立
在进行砌体结构拆除造价预测时,首先针对砌体待拆除建筑进行影响因素的选取,通过文献阅读,随机抽取了拆除公司在长春市砌体拆除工程50组工程案例进行对比分析,此模型仅针对长春市砌体拆除工程进行了研究.选取了10种主要影响因素,分别为拆除方法、工程所在位置、房屋危险等级、墙体厚度、噪音、污染程度、建筑面积、抗震设防烈度、墙体总长、工程总层数[12].这些影响因素需要将其量化数据才能带入Matlab软件进行运行.例如在砌体拆除方法中,采用人工拆除的取1,全机械取2,半人工半机械取3[13-14],其他工程影响因素量化指标通过查阅相关资料进行定性定量分析得到见表1.

表1 影响因素量化指标Table 1 Quantitative index of influencing factor
上述为50组砌体拆除工程的相关案例的数据,其中40组数据用于训练网络模型,另外10组数据用于检测网络模型,对其进行量化分析整理见表2,表3.表2为训练样本数据,表3为检测样本数据.

表2 砌体拆除训练样本原始数据Table 2 Original data of masonry demolition training samples

续表2
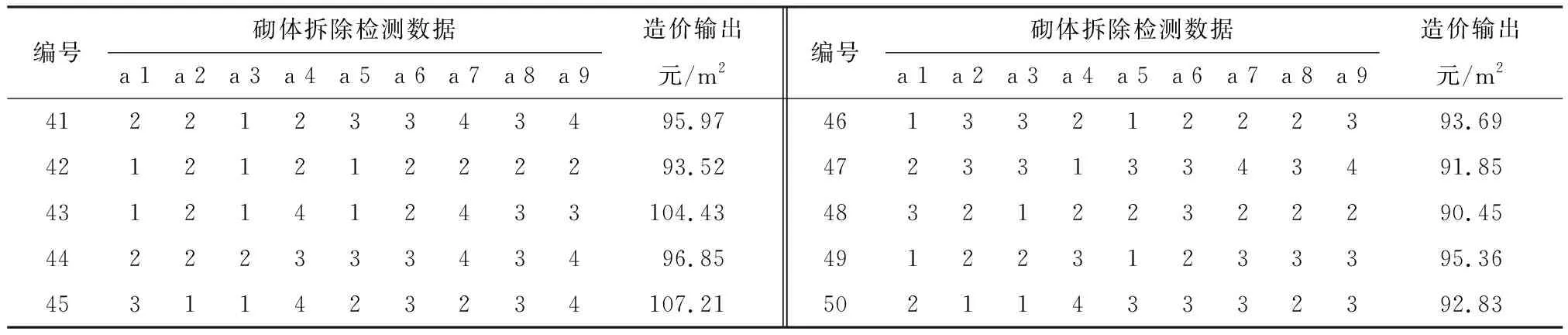
表3 砌体拆除检测样本原始数据Table 3 Original data of masonry demolition test samples
BP神经网络及GA-BP神经网络主要参数设置,见表4.

表4 网络参数设置Table 4 Network parameter settings
经过训练验证,两种算法输出结果如图2所示.
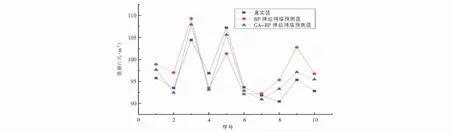
图2 两种神经网络输出结果对比Fig.2 Comparison of output results of the two neural networks
对两种算法得出的预测值计算出的相对误差值进行对比,BP神经网络的平均误差值为3.99 %,均方误差值为18.60;而遗传算法优化后的BP神经网络的平均误差值为2.13 %,均方误差值为5.22.由上述的数据结果分析可知,GA-BP神经网络相对于BP神经网络性能更优越.
5 结论
本文运用遗传算法优化BP神经网络针对砌体结构拆除阶段造价进行预测拟合,未经过优化的BP神经网络造价预测误差为4.01 %,采用遗传算法优化的神经网络预测造价误差为2.15 %,准确度和稳定性均有较大提高,在利用智能优化算法对砌体拆除造价预测领域具有一定的参考价值.该模型经过学习训练后能在误差允许的范围内对长春市砌体拆除工程的造价进行预测,达到快速估算要求,具有良好的可行性.

