太赫兹频段六角形冰晶粒子散射和吸收特性

高宇洁 陈 健 朱 琳 李雪莲 李春晖 陈德海

（南京信息工程大学遥感与测绘工程学院，江苏 南京 210044）

0 引言

卷云可以通过散射太阳辐射、吸收地表长波辐射来调控地-气系统的温度。政府间气候变化专门委员会（Intergovernmental Panel on Climate Change，IPCC）第四次评估报告[1]关注了卷云所具有的气候效因。传统方法以实心匀质的球形粒子为前提，利用Mie散射理论研究卷云辐射特性，但实际卷云多为六角形粒子，因此该理论不适用。近年来，一些学者开始深入研究非球形粒子的辐射特性。例如王玉文等人利用T-matrix方法建立了对称非球形冰晶粒子的衰减模型[2]。吴举秀等人使用离散偶极子近似法（Discrete Dipole Approximation，DDA）研究了取向、形状和温度对94 GHz冰晶散射效率的影响[3]。王颖等人研究了非球形粒子的散射矩阵[4]。类成新研究了随机取向六角形粒子的散射特征量及敏感程度[5]。探测卷云时，可见光与近红外穿透性过弱，微波穿透性过强，而太赫兹波段（30 μm~3 000 μm）[6]和卷云冰晶粒子（50 μm~400 μm）位于同一量级，能够获取更全面的回波信息，理论上为探测卷云的最佳波段[7]。该文将利用DDA算法模拟球形粒子在太赫兹频段下的辐射结果，并与相同频率下Mie散射结果进行对比，以评估DDA方法的计算精度；在该基础上计算了340 GHz六角形冰晶粒子的辐射特性，重点分析了不同纵横比和不同空间取向对辐射特性的影响。

1 DDA方法原理介绍

DDA方法是当前被广泛使用的数值计算方法，非常适合用来研究六角形粒子的散射和吸收特性。它可以通过大量离散偶极子模拟计算不同入射方向、不同入射波长以及不同形状情况下粒子的散射和吸收系数[8]。其基本思想如下：散射特性较连续的物体可近似为可极化点阵。为了从该近似点阵中获得偶极子，可对该点阵中各个点对局域电场（入射场及其他点的辐射场都包括在内）进行研究。在上述方法中，单个粒子的散射特性是连续的，因此将这些具有连续散射特性的单个粒子转化为多个离散偶极子阵列，这些偶极子始终具有呈周期性排列及相互作用的特性。在整个过程中，点阵中每一个点受局域电场的影响生成偶极矩，最终这些点的辐射总和形成了散射场。

在近似点阵中，已知共有n个偶极子，假设第k个偶极子的坐标为rk（k=1，2，…，n），该处电场强度为Ek，偶极矩（即极化强度）为Pk；第j个偶极子的坐标为rj（j=1，2，…，n），该处电场强度为Ej，偶极子极化率为αj，则该点的偶极矩Pj如公式（1）所示。

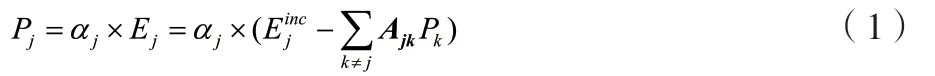
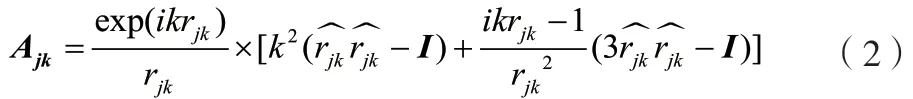
式中：i为虚数单位；k为波数，（λ为入射波长）；rjk为第j个偶极子与第k个偶极子间的距离，；I为 3×3 的单位矩阵；为第k个偶极子到第j个偶极子的单位向量。

通过公式（3）可解出Pk，由此得出第j个偶极子电偶极矩为Pj，在该情况下能够获得该核壳结构粒子的消光截面Cext、吸收截面Cabs、散射截面Csca以及其他辐射特征量。

该核壳结构粒子的消光截面Cext、消光系数Qext如公式（4）、公式（5）所示。

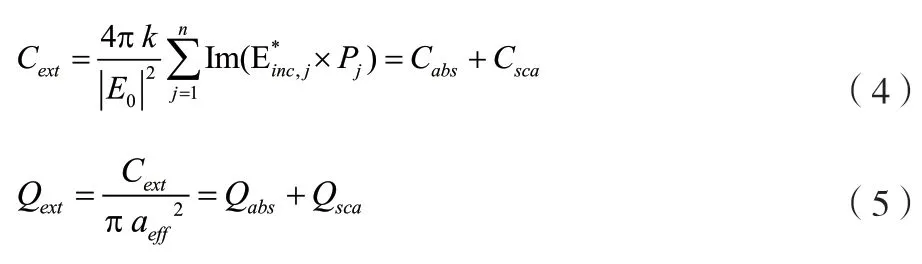
式中：E0为原点处的电场强度；E*inc,j为第个偶极子的入射波电场强度的复共轭；Qsca为散射系数。

吸收截面Cabs、吸收系数Qabs如公式（6）、公式（7）所示。

散射截面Csca、散射系数Qsca如公式（8）、公式（9）所示。

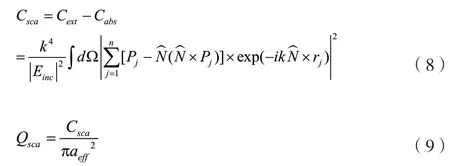
式中：dΩ为立体角微元；为散射方向单位矢量；aeff为粒子等体积球的等效半径，；Einc为入射波电场强度；*为该值取复共轭[9]。

研究结果表明，离散偶极子近似法在微粒折射率m≈1时其精度最高，m取值离1越远，计算精度越低。当存在较大的折射率|m|或kaeff的情况时，如果想更精准地模拟粒子的光散射，就需要更多数量的偶极子[10]。

2 DDA方法的精度评估

以往DDA的研究多是针对毫米波、可见光的，而针对太赫兹的研究较少，该文首先对大气透过率较高的340 GHz频段下DDA的计算精度进行分析。由于Mie散射理论是由麦克斯韦方程组推导出的求解球形粒子散射特性的经典算法，因此可以将Mie散射结果作为标准值，以评估相同条件下DDA方法的计算结果精度。鉴于计算机性能和DDA算法的限制，该文模拟的球形冰晶粒子等效半径范围为50 μm~1 000 μm，步长为10 μm，球形冰晶粒子在340 GHz频段下的复折射指数为1.782+0.0071i（i为虚数单位），其他参数选用DDA的默认设置。图1描述了340 GHz频段下球形冰晶粒子的辐射特性随等效半径变化而变化的规律。

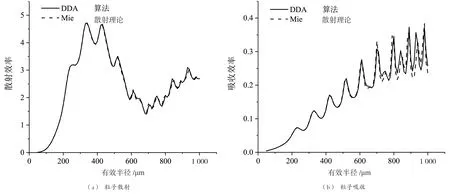
图1 球形冰晶粒子辐射结果

由图1（a）可知，在340 GHz频段下由DDA算法和Mie散射理论计算得到的球形冰晶粒子散射曲线几乎完全重合。等效半径小于600 μm时，散射效率相对误差稳定，在0.5%上下浮动；大于该范围后，随着等效半径的增加，相对误差波动上升，最高大约为5%。由图1（b）可知，在该频段下2种方法计算得到的粒子吸收曲线大部分都重合，当等效半径小于600 μm时，吸收效率相对误差较稳定，最大不超过2%；大于该范围后，相对误差增加，在10%附近上下波动且等效半径为930 μm时的吸收相对误差最大。

综上所述，在340 GHz频段下随着等效半径的增加，散射和吸收效率的相对误差逐渐增大。对DDA算法来说，这是由于偶极子数目变少而导致的。无量纲尺度参数（如公式（10）所示）描述了给定的散射问题，而DDA算法不适用于尺度参数x非常大的粒子。由粒子大小aeff和偶极子间距d之间的关系（如公式（11）所示）可知，当粒子等效半径增大时，偶极子间距也变大，为了满足约束条件，偶极子数目将会减少，计算结果的精度也随之下降。因此计算高频率下的大尺度粒子时得到的结果误差较大。

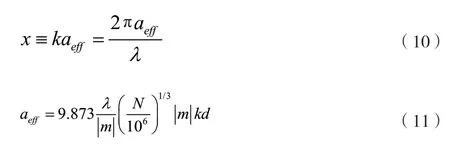
比较图1（a）和图1（b）还可以发现，冰晶粒子的吸收效率远小于散射效率，因为粒子本身吸收较小，此时偶极子数量减少所带来的相对误差就比较明显。综合图1可以得到以下结论：当有效半径小于600 μm时，无论是散射和吸收，其相对误差均小于2%，因此使用DDA方法仍然会具有较高精度。当有效半径大于600 μm时，误差随半径增加而增加，但由于吸收效率的绝对值较小，因此仍然可以使用DDA算法，但其可靠性会降低。

3 六角形冰晶粒子散射和吸收特性研究

与球形粒子相比，六角形粒子的纵横比、空间取向不同，对应电磁波的散射和吸收特性也不同，因此有必要研究不同纵横比、不同空间取向以及不同粒子大小情况下冰晶粒子的散射和吸收特性，为准确地进行卷云参数遥感反演提供依据。该文通过DDA方法建立六角形冰晶粒子的物理模型，计算在340 GHz频率下不同纵横比、不同空间取向下不同有效半径的粒子散射和吸收效率，进而分析纵横比和空间取向的影响。其中纵横比分别取4、2、1、1/6和1/20；空间取向的极化角φ、β都取0°，θ角取值范围为0°~90°且步长为1°。

3.1 球形粒子与六角形粒子的比较

假设卷云中存在的冰晶粒子均为球形，此处选取极化角θ为0°、纵横比为1的球形冰晶粒子，即块柱状六角形冰晶粒子为代表。如图2（a）所示，描述了2种冰晶粒子的散射特性随有效半径增大而波动变化的特点，当有效半径较大时，块柱状六角形冰晶粒子的散射特性比球形冰晶粒子的波动幅度更大。如图2（b）所示，描述了2种冰晶粒子的吸收特性随有效半径增大而波动增加的变化特点，但球形冰晶粒子与六角形冰晶粒子的吸收特性在粒子大小不同的情况下，其数值并不一致。综上所述，球形与六角形的冰晶粒子在340 GHz频段下会产生不同的散射和吸收特性，进一步证明太赫兹为探测卷云的最佳波段，如果将卷云粒子假设为球形粒子会带来较大的误差，因此该假设不成立，无法使用球形冰晶粒子代替六角形冰晶粒子。

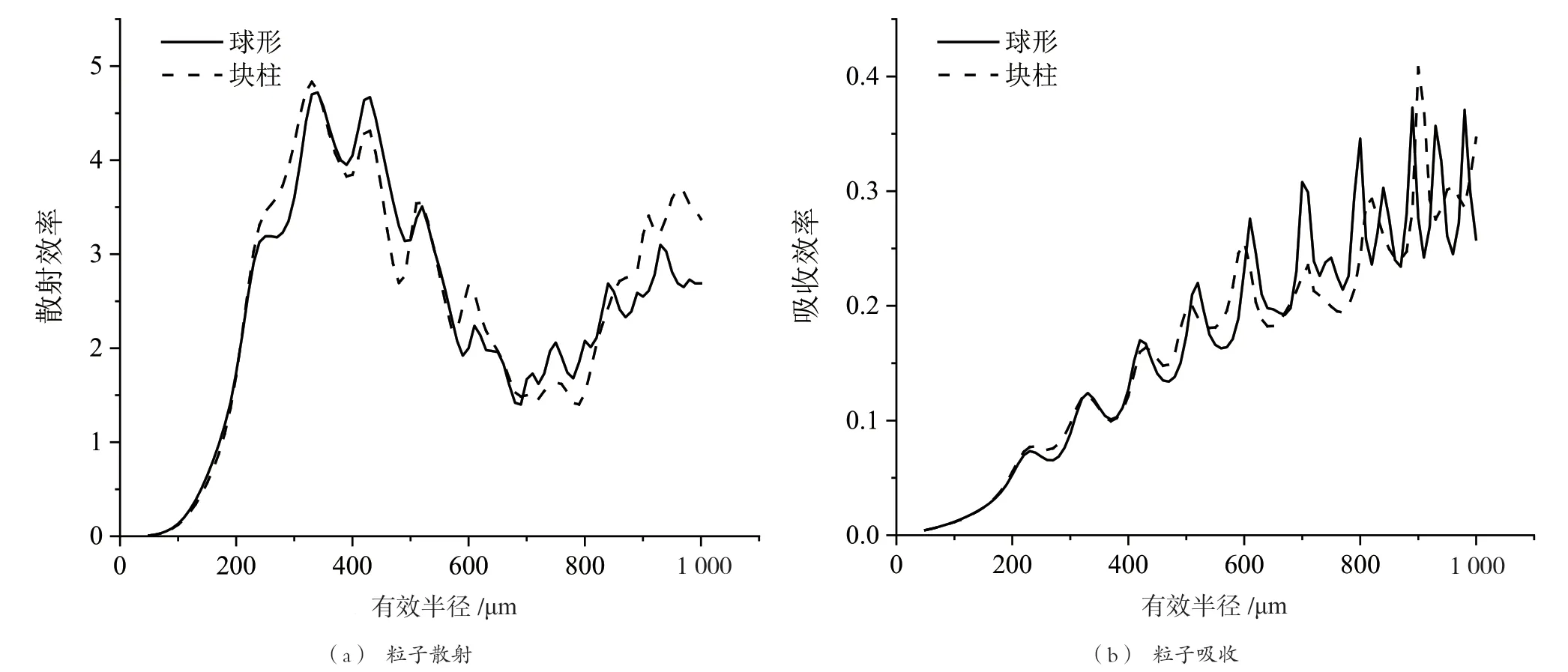
图2 球形与六角形冰晶粒子辐射结果

3.2 不同纵横比的影响

六角形粒子的形状可以由高L和边长a来描述，纵横比定义为L/2a，当纵横比分别为4、2、1、1/6和1/20时，六角形粒子可以分别称为长柱、厚柱、块柱、厚板和薄板。该文研究了在340 GHz频段下不同纵横比粒子的散射和吸收特性，如图3所示。

图3 六角形冰晶粒子辐射结果

由图3可见，在340 GHz频段下，纵横比为4的六角形冰晶粒子散射曲线波动很大，存在3个峰值，分别位于360 μm、560 μm以及830 μm处；纵横比为2、1的六角形冰晶粒子散射特性曲线波动相对明显，存在2个峰值，且随着有效半径的增加，其峰处对应数值变小；而纵横比为1/6、1/20的粒子散射特性总体趋势随有效半径的增加而增加，在有效半径大于400 μm的部分散射数值大于另外3个散射数值。相比于散射特性，不同纵横比下的六角形冰晶粒子的吸收特性曲线变化规律更一致，在所有纵横比情况下都呈现波动上升的趋势，纵横比越大，曲线的峰值越多，且相同半径下不同纵横比的粒子吸收数值相差不大。

综上可得，在340 GHz频段下相同空间取向的冰晶粒子纵横比越大，辐射特性曲线越陡峭、峰值越多且散射曲线变化越复杂，而吸收曲线变化规律相同且都为上升趋势。吴举秀等人[3]对六角形冰晶的94 GHz毫米波后向散射特性进行模拟、计算和分析，在冰晶后向散射效率对形状的敏感性方面得出了相似的结论。当粒子的纵横比远离1时，它的形状偏离球形，相同尺度下粒子的最大截面积也越大，因此厚板和薄板粒子的后向散射也就越大。

3.3 不同空间取向的影响

当粒子的形状为非球形时，其散射和吸收特性参数与光束入射角有关，相同粒子在固定的坐标系中会因空间取向不同而引起不同的光学特性，因此在研究非球形粒子的散射和吸收特性时应该考虑其空间取向。空间取向指非球形粒子在空间所摆放的位置，建立如图4所示的坐标系：系统坐标系和固定于粒子的当地坐标系a1-a2-a3[11]，取向主要由极化角θ、φ和β来决定，其中θ为a1与轴之间的夹角，φ为a1与平面之间的夹角，β为a2与Xa1平面之间的夹角。该文选取340 GHz频段下、纵横比为2的厚柱和纵横比为1/6的厚板状六角形冰晶粒子在空间中从横放到竖放的变化过程，模拟正常情况下不同入射角时粒子空间取向对其辐射特性的影响，而理论上极化角θ与入射角的大小相同，因此θ从0°到90°以1°为步长各取1个空间取向进行分析，其他极化角为0°。

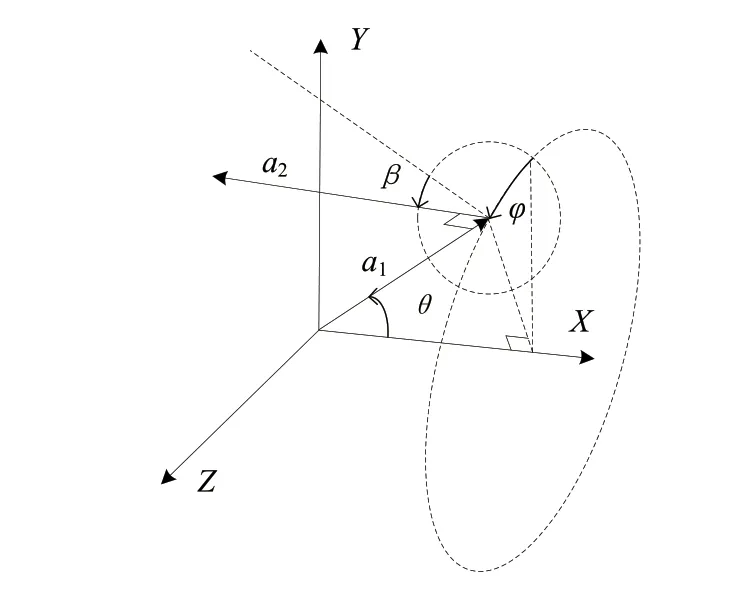
图4 非球形粒子在系统坐标中的取向

当纵横比为1/6时，在340 GHz频段下不同空间取向的厚板状六角形冰晶粒子的散射和吸收特性如图5所示（以空间取向为0°、15°、30°、45°、60°、75°以及90°的辐射特性为代表）。由图5（a）可知，当粒子等效半径范围为50 μm~1 000 μm时，由于空间取向的变化，随着粒子等效半径的增大，散射特性曲线的变化趋势各不相同，整体上曲线先波动上升，增加到一个峰值后再波动下降。并且随着空间取向的增加，散射特性曲线变化越来越剧烈、峰值处对应的等效半径越来越小。在横纵比相同的情况下，当粒子尺度较小时，空间取向值大的粒子的散射效率大于空间取向小的粒子；随着粒子尺度的增加，空间取向值大的粒子的散射效率逐渐小于空间取向值小的粒子。

由图5（b）可知，吸收特性曲线整体上呈现出上升的趋势；随着空间取向的增加，曲线越来越陡峭，且在粒子尺度较大的部分，波动越来越剧烈。在粒子尺度小于500 μm 的部分，空间取向越大的粒子的吸收效率就越大；而后半部分的粒子吸收效率随着空间取向的增大先增加后减少。

图5 六角板的散射和吸收特性

当纵横比为2时，在340 GHz频段下不同空间取向的厚柱状六角形冰晶粒子的散射和吸收特性如图6所示。由图6（a）可知，随着空间取向的增大，散射特性曲线由先上升到峰值后下降又继续上升的多峰值波动趋势，变为整体波动先上升后下降的趋势，即曲线的整体趋势从两端凸起、中间下凹变成中间凸起。并且随着空间取向的增大，散射峰值先减少后增加，曲线变化越来越平缓。

由图6（b）可知，吸收特性曲线波动上升，随着空间取向的增大，曲线波动由较剧烈变为平缓。且在相同空间取向的情况下，随着粒子尺度的增加，曲线波动越来越明显。

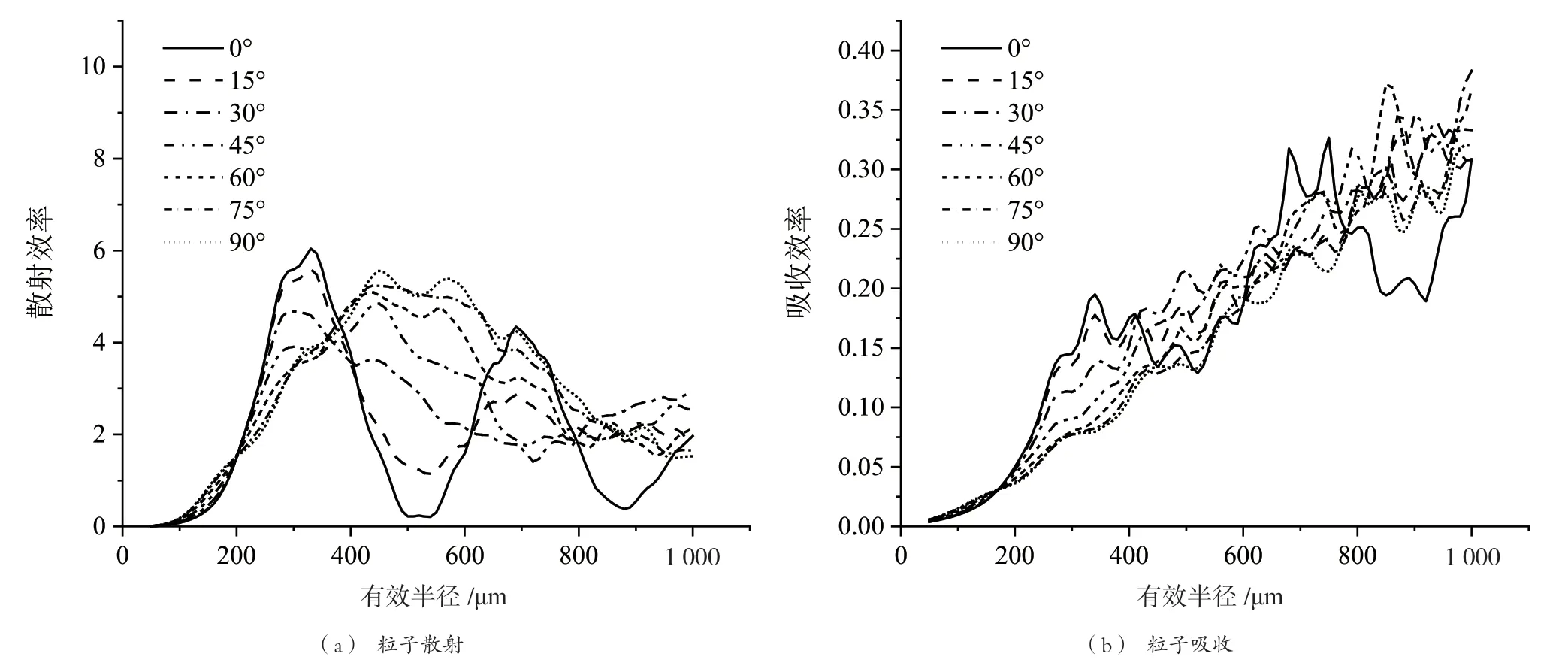
图6 六角柱的散射和吸收特性

综上所述，在纵横比相同的情况下，散射和吸收特性随粒子等效半径变化而变化的趋势与空间取向有关。当粒子尺度较小时，不同空间取向对六角形冰晶粒子辐射特性的影响较小，整体上随等效半径的增加而增加；当粒子尺度较大时，不同取向引起的散射截面差异被放大。这是因大尺度粒子具有较大的散射截面，微小的空间取向差异会使其散射截面产生较大的变化而导致的。对比柱状和板状的六角形冰晶粒子对应的散射和吸收特性曲线与空间取向的关系可以发现，六角板冰晶粒子受空间取向的影响较大，其原因可能为柱状冰晶比板状冰晶更接近球形，其光学特性受空间取向影响的敏感性与粒子形状有关。粒子纵横比偏离1越多，其形状越偏离球形，不同取向下散射截面的差异也就越大，光学特性受空间取向影响越敏感[3]；粒子纵横比越接近1，其形状越接近球形，辐射特性就越近似于各向同性，光学特性受空间取向的影响较小。

4 结论

通过对比验算得出在DDA算法可用尺度内[12]，粒子辐射的计算具有较高的精度。因此该文在340 GHz频段使用该方法计算等效半径为50 μm~1 000 μm的六角形冰晶粒子辐射特性，着重分析了不同纵横比、不同空间取向对卷云冰晶粒子辐射特性的影响。结果表明：1） 在340 GHz频段下，通过比较Mie散射理论和DDA计算得到的球形粒子辐射结果可以发现，2种方法得到的辐射曲线几乎一致，但随着等效半径的增加，相对误差整体增大，且散射误差最大不超过5%，吸收误差最大约为10%。因此在340 GHz频段使用DDA方法计算常见冰晶粒子（尺度在1 000 μm以内）的辐射特性具有较高的精度。2） 空间取向一定时，不同纵横比的六角形冰晶粒子辐射特性不同。纵横比越大，粒子的散射特性曲线更陡峭、波动更明显，而吸收特性曲线整体呈上升的趋势。粒子纵横比偏离1越多，相同尺度下粒子的最大截面积就越大，厚板和薄板冰晶粒子的后向散射也就越大。3） 纵横比一定时，空间取向差别较大的六角形冰晶粒子辐射特性不同。随着等效半径的增大，不同取向引起的散射截面差异被放大。粒子纵横比偏离1越多，微小的空间取向差异会使其散射截面产生较大的变化，光学特性受空间取向影响越敏感；反之，辐射特性就越近似于各向同性，光学特性受空间取向的影响较小。