自动驾驶模糊神经网络速度规划方法*

王 猛,陈珏璇,邓正兴

(1.华中科技大学人工智能与自动化学院,湖北 武汉 430074;2.武汉光庭信息技术股份有限公司K+Lab实验室,湖北 武汉 430073;3.武汉光庭科技有限公司智能驾驶部,湖北 武汉 430200)

1 引言

自动驾驶是当前研究热点，但仍然存在着安全性、稳定性和舒适性等方面的不足，研究者也在从不同方面进行改进和优化[1]。运动规划作为自动驾驶的核心环节之一[2,3]，其功能是生成自动驾驶车辆的运动轨迹，以躲避行驶路线上的障碍物，该轨迹包含了车辆行驶的路径和以何种速度(加速度)运动的信息。运动规划相关研究主要有启发式搜索算法、人工势场法和离散优化方法等[4]。文献[5]指出，由于动态障碍物的存在，运动规划方法需要将时间作为一个维度，叠加在路径搜索、路径生成环节后的空间轨迹上，构成时间和空间上的可行轨迹。空间和时间维度的叠加计算会增加算法的时间复杂度。文献[6]提出了路径-速度分解法，先构造一条曲率连续有界的可行路径，再在该路径上规划速度。文献[7,8]在生成的最优路径基础上，建立每个路径点的速度(加速度)与时间和路径长度的关系模型，合成时间和空间上的运动轨迹。此类方法能够保证速度规划的连续性和平滑性，但生成的运动轨迹，尤其是速度轨迹，难以在后继控制模块中准确跟踪[9]，因而无法满足设计初衷。

为了降低自动驾驶运动规划的计算复杂度，保证自动驾驶的舒适性和稳定性，本文提出了一种基于模糊神经网络的智能化速度规划方法。相比于现有的速度规划方法，本文方法具有以下特点：(1)直接计算实时期望加速度，而不是生成速度曲线，能够降低速度规划的计算时耗，工程实现极为简便；(2)计算的加速度连续平稳变化，易于后继控制模块准确跟踪；(3)分析了典型场景，建立了不同的模糊神经网络速度规划模型，以匹配自动驾驶车辆复杂的驾驶行为。

2 自动驾驶运动规划方案

通常自动驾驶的功能软件由3个模块构成，即感知定位模块、决策规划模块和控制模块。

2.1 自动驾驶的功能软件整体结构

自动驾驶的功能软件整体结构如图1所示。感知定位模块包含感知模块和定位模块，其中，感知模块获取环境信息；定位模块通过高精度惯导获取位置、航向和速度等信息；决策规划模块规划局部路径以及速度、加速度信息；控制模块负责轨迹跟踪控制和纵向速度跟踪控制。另外，人机交互HMI(Human Machine Interface)处理部分处理与外部的交互信息，CAN总线处理负责输入和输出控制信息。

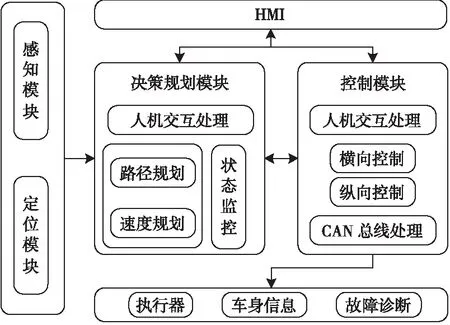
Figure 1 Block diagram of functional software of autonomous vehicle图1 自动驾驶功能软件框图

2.2 自动驾驶运动规划

运动规划模块是决策规划模块的核心模块之一。本文中，运动规划采用了路径-速度分解法，首先进行路径规划，获得局部最优路径，然后进行速度规划，最终合成空间和时间轨迹。

(1) 路径规划方法。

本文采用状态格算法[10]进行路径规划，将道路进行网格化处理，道路网格沿道路参考线分布，并随参考线方向延伸。每个网格格点定义为状态格点，且状态格点的方向和曲率中心点与道路参考线一致，如图2所示。基于状态格的路径规划流程如图3所示。具体描述如下：①构建状态格，确定状态向量。按照参考线延伸方向划分网格格点，依据路径-速度分解法，本文仅考虑空间维度，即每个格点的状态量包含位置、方向和曲率半径。②路径生成。以5次多项式函数作为连接曲线，结合车辆运动学模型，采用梯度下降法求解5次多项式，生成每2个状态格点间的连接曲线。③设计评价函数。考虑安全性能、舒适性能和能耗性能等，设计评价函数计算每段曲线的代价函数值。④路径寻优。计算从当前点到目标点综合性能最优的路径，作为最优路径。

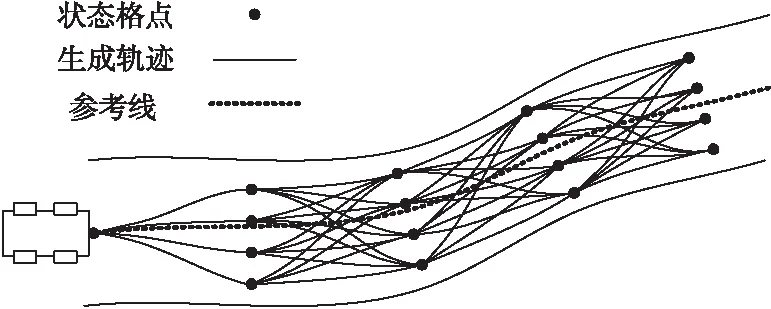
Figure 2 Schematic diagram of path planning图2 路径规划示意图

Figure 3 Flow chart of path planning图3 路径规划流程

(2) 速度规划方法。

在前文已经规划出的最优路径上，若存在有停止线、指定停车点、静止障碍物或动态障碍物等，速度规划模块将根据这些信息以及到自车的距离，实时规划加(减)速度，发送至控制模块执行，使车辆减速停车或跟随动态障碍物行驶。本文提出的速度规划方法将上述场景归纳为2类：遇静态障碍物场景和遇动态障碍物场景。分别构建2类场景模型，然后针对上述2类模型，设计静态障碍物场景速度规划算法和动态障碍物场景速度规划算法，最后对算法输出进行速度信息处理。速度规划方法的流程如图4所示。具体步骤为：①实时获取感知定位信息。速度规划模块从感知模块和定位模块读取前方障碍物信息(动静态、距离和速度等)，从地图系统获得停止线或终点线信息(包括类型和位置等)。②分别构建2种场景模型。自动驾驶车辆遇到前方有停止线、终点线或设定停车点等场景时，车辆都应该降速停车，这些场景等同于自动驾驶车辆遇到前方静态障碍物而降速停车，因此将此类场景统一归类为遇静态障碍物场景。对于遇动态障碍物的场景，如前方有行驶车辆等，速度规划方法应生成实时加(减)速度指令，使得车辆跟随动态障碍物行驶，因此归类为遇动态障碍物的场景，分别建立2类场景的模型。③分别针对静态障碍物和动态障碍物2种场景模型设计基于模糊神经网络的速度规划方法，将在下节详述。④速度信息处理。评价2类场景的规划结果，以加速度较小者作为输出，并对规划结果进行平滑和限幅等处理。

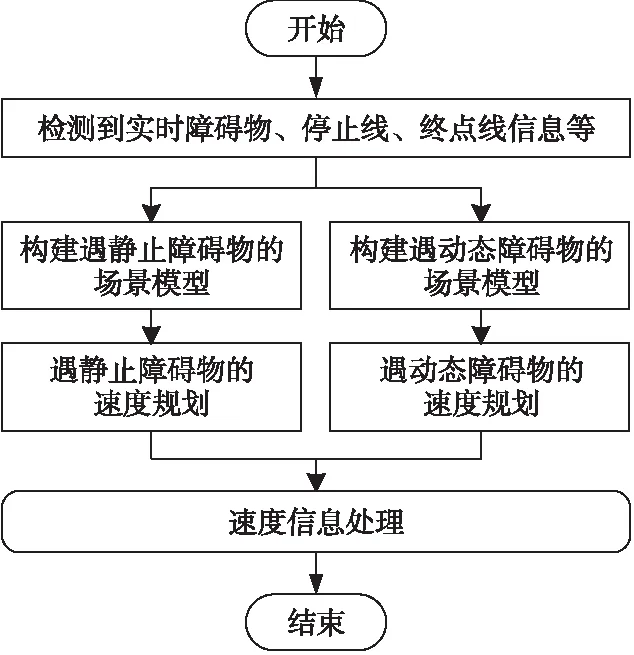
Figure 4 Flow chart of velocity planning图4 速度规划流程

3 基于模糊神经网络的速度规划方法

速度规划模块的功能是根据道路环境及自车状态，实时计算出车辆的期望加速度[11]。本文提出了基于模糊神经网络的速度规划方法，用于建立从输入状态量到输出加速度的神经网络模型。

3.1 基于模糊神经网络的速度规划方法原理

基于模糊神经网络的速度规划方法分为离线学习和在线计算2个阶段。

(1) 离线学习阶段。

将人工驾驶经验总结为模糊规则表(模糊规划模型)。然后提取模糊规则表中每个规则转化为输入输出样本，构成样本集合。初始化一个3层结构的神经网络模型，利用样本集合，离线训练神经网络，获得离线训练后的神经网络模型，将其定义为模糊神经网络规划模型。

模糊规划模型描述了输入状态量到输出量的映射关系。自动驾驶车辆遇到动、静障碍物时，主要依据自车与障碍物之间相对位置和速度关系，推算目标加速度。定义距离状态量为d，速度状态量为v，将输入状态变量分别模糊化为语言变量集合D和V：

V={V1,V2,…,Vi,…,Vm}

(1)

D={D1,D2,…,Dj,…,Dn}

(2)

其中，m、n分别为距离状态量和速度状态量的语言变量数量。

定义输出量为a，将输出量模糊化为语言变量集合A：

A={A1,A2,…,Ak,…,Al}

(3)

其中，l为输出语言变量的数量。

式(1)～式(3)中，为了便于后续统一分析，用语言变量Vi、Dj和Ak代替常规的语言变量，例如负大NB(Negative Big)、负小NS(Negative Small)、正大PB(Positive Big)等。根据模糊系统理论，首先对每个输入变量和输出变量建立隶属度函数，如图5所示。结合人工驾驶经验，建立模糊规则表，如表1所示。

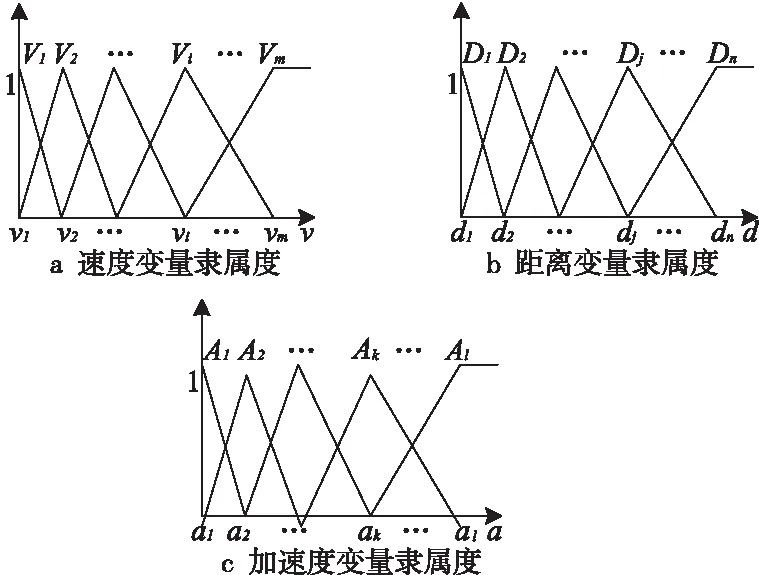
Figure 5 Membership functions图5 隶属度函数

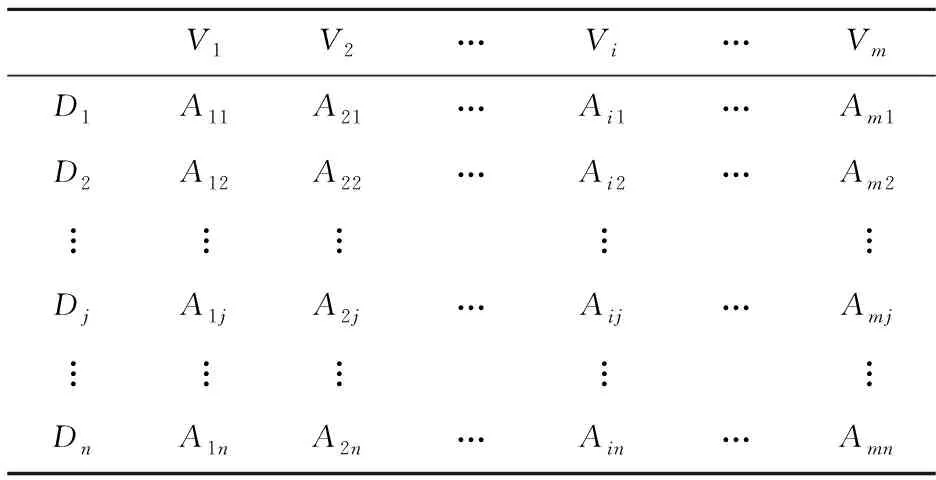
Table 1 Fuzzy rule table A

表1中，第i个速度语言变量Vi与第j个距离语言变量Dj作为输入时，所对应的加速度输出语言变量为Aij，且Aij∈A。

根据建立的模糊规则表和变量的隶属度函数，可以建立速度规划模型，该模型描述了输入状态量到输出量的映射关系，即aij=f(vi,dj),其中，vi、dj和aij分别为语言变量Vi、Dj和Aij的最大隶属度值。提取模糊规则表1中的每个规则，如第[i,j]个规则为Sij=[Vi,Dj,Ak]，取语言变量Vi、Dj和Ak的最大隶属度对应的实数域值为vi、dj和ak，则对应的第[i,j]个样本为sij=[vi,dj,ak]。由此，构成了m×n个输入输出样本集合，如式(4)所示：

sij=[vi,dj,ak],

i=1,2,…,m;j=1,2,…,n;k=1,2,…,l

(4)

建立3层神经网络模型，其中输入层神经元数量为输入状态量数目，隐含层神经元数量为N，输出层神经元数量为输出量数目。神经网络输入层到隐含层、隐含层到输出层的权值向量分别为w1和w2，隐含层和输出层的偏置向量分别为b1和b2，隐含层和输出层采用的传输函数为双曲正切函数(tansig)。将sij作为学习样本，采用BP算法训练神经网络的权值向量和偏置向量，反向训练过程如式(5)～式(8)所示[12]：

(5)

(6)

(7)

(8)

其中，k为迭代训练次数，Δw和Δb为BP算法的调整量。最后，将训练好的神经网络模型作为模糊神经网络速度规划模型。

(2) 在线计算阶段。

实时读取距离状态量dt和速度状态量vt，然后将这2个状态量作为模糊神经网络规划模型的输入，在线计算加速度，在线计算公式如式(9)所示：

a′t=tansig(w2·tansig(w1·[v′t,d′t]T+b1)+b2)

(9)

其中，a′t,v′t,d′t分别为归一化的加速度、速度状态量和距离状态量，w1，w2,b1和b2分别为训练好的神经网络权值向量和偏置向量。最后，将a′t反归一化作为输出。

3.2 静态障碍物速度规划模型

对于遇静态障碍物的场景，目标是规划出实时减速度，使车辆在障碍物前平稳降速。本文研究的自动驾驶车辆最高车速为70 km/h，因此取自车速度为[0,20]，单位为m/s,将自车速度模糊化为12(m=12)个模糊语言构成的模糊集合V={V1,V2,…,V12}，以三角函数作为隶属度函数，利用模糊神经网络速度规划方法，分别确定模糊语言最大隶属度对应的实数值如式(10)所示：

v={v1,v2,…,v12}=

{1,2,3,4,5.5,7,8.5,10,12,14,16,20}

(10)

感知系统稳定的探测距离为110 m，因此取自车到目标点的距离为[0,110]，单位为m,将距离模糊化为9(n=9)个模糊语言构成的模糊集合D={D1,D2,…,D9}，以三角函数作为隶属度函数，利用模糊神经网络速度规划方法，分别确定最大隶属度对应的实数值如式(11)所示：

d={d1,d2,…,d9}=

{2,5,9,15,24,37,55,79,110}

(11)

乘用车制动系统能够提供0.7g以内的减速度，因此取加速度为[-6,0]，单位为m/s2,将加速度模糊化为11(l=11)个元素构成的模糊集合A={A1,A2,…,A11}，确定最大隶属度对应的实数值如式(12)所示：

a={a1,a2,…,a11}={-6,-5,-4,-3,

-2.5,-2,-1.5,-1,-0.5,-0.25,0}

(12)

速度、距离和加速度变量对应的隶属度如图6所示。

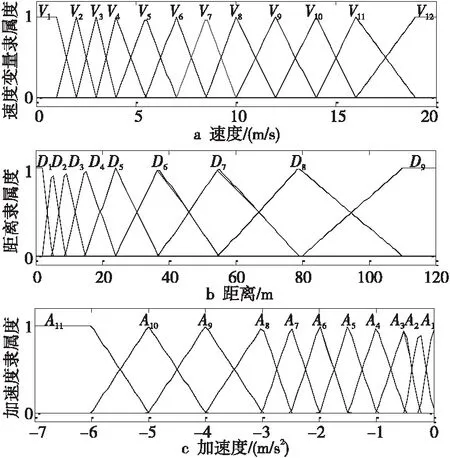
Figure 6 Membership functions of all variables when encountering statics obstacles图6 遇静态障碍物时各变量的隶属度函数

结合人工驾驶经验，以自车速度和到障碍物的距离作为输入，以期望加速度作为输出，建立表2所示的模糊规则表，得到模糊速度规划模型，如图7所示。

由图7可知，模糊速度规划模型明显存在加速度平面不平滑的现象，容易导致自动驾驶车辆因顿挫感带来的舒适性差的问题。为此，本文将模糊速度规划模型的模糊规则转化为输入输出样本集合，利用神经网络自学习的功能，离线修正规划模型。

Table 2 Fuzzy rule table A in static obstacle scenes表2 遇静态障碍物场景的模糊规则表A

将车速集合v和距离集合d中的元素组合，形成由108个样本构成的输入样本集合，如式(13)所示：

Figure 7 Fuzzy planning model in static obstacle scenes图7 遇静态障碍物场景的模糊规划模型

P={[vi,dj]|vi∈v,dj∈d,

i=1,2,…,12;j=1,2,…,9}

(13)

根据模糊规则表查找相对应的加速度aij，形成由108个元素构成的输出样本集合，如式(14)所示：

T={aij|i=1,2,…,12;j=1,2,…,9}

(14)

由此可得，遇静态障碍物场景模糊规划模型的样本集合如表3所示。

对于任意元素vi∈v,dj∈d，按照式(15)对输出加速度样本进行检验，以满足安全性能：

(15)

对输入输出样本集合对[P,T]中的每一个样本[vi,dj,aij]，按式(16)进行归一化处理，获得归一化后的输入输出样本集合对[P′,T′]。

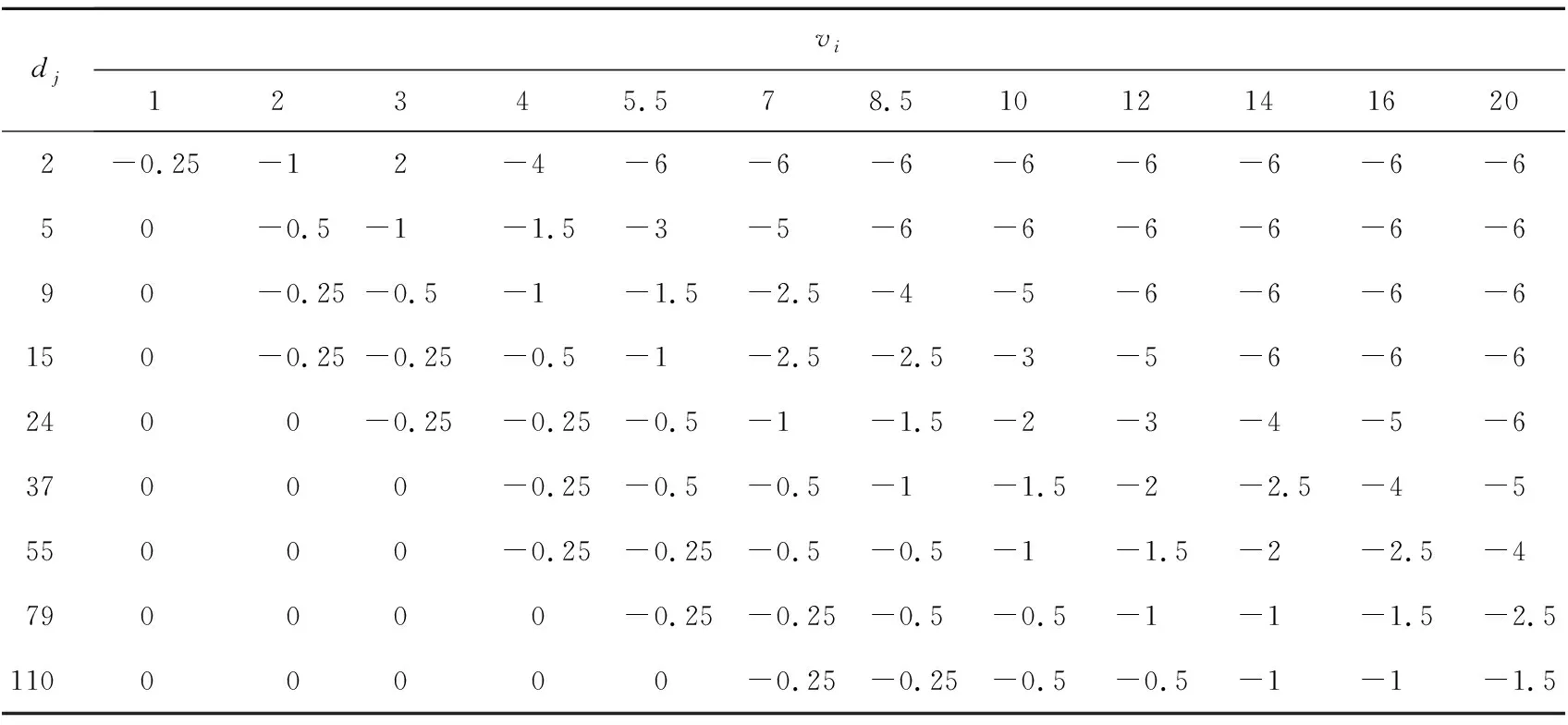
Table 3 Sample set T in static obstacle scenes表3 遇静态障碍物场景的样本集合T

(16)

建立3层神经网络模型，以输入输出样本集合对[P′,T′]作为训练样本，离线训练神经网络，获得神经网络的权值向量和偏置向量。最后，以训练好的神经网络作为速度规划模型，以自动驾驶车辆实时车速、到静止障碍物的距离作为神经网络规划模型的输入，在线计算加速度。图8为训练好的神经网络规划模型，可知该速度规划模型相比于模糊规划模型，加速度平面更加光滑，因此能够提高自动驾驶的舒适性。

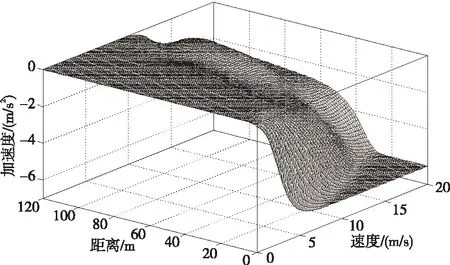
Figure 8 Fuzzy neural network planning model in static obstacle scenes图8 遇静态障碍物场景的模糊神经网络规划模型

3.3 动态障碍物速度规划模型

对于遇动态障碍物的场景，速度规划的目标是规划出实时加速度，使自动驾驶车辆跟随障碍物，并保持较稳定的安全距离。在该场景中，速度状态量有障碍物速度vO和自车速度vS，距离状态量为自动驾驶车辆到障碍物的距离d。为减少规划模型的维度，将输入状态量定义为相对速度Δv=vS-vO(单位为m/s)和时距τ=d/vS(单位为s)。确定相对速度为[-7,7],单位为m/s，时距为[0,6],单位为s。跟车时距设定为τset=2.5 s。分别定义相对速度、时距和期望加速度的模糊语言集合为：V={V1,V2,…,V9}，D={D1,D2,…,D10}，A={A1,A2,…,A14}，其对应的隶属度函数如图9所示。

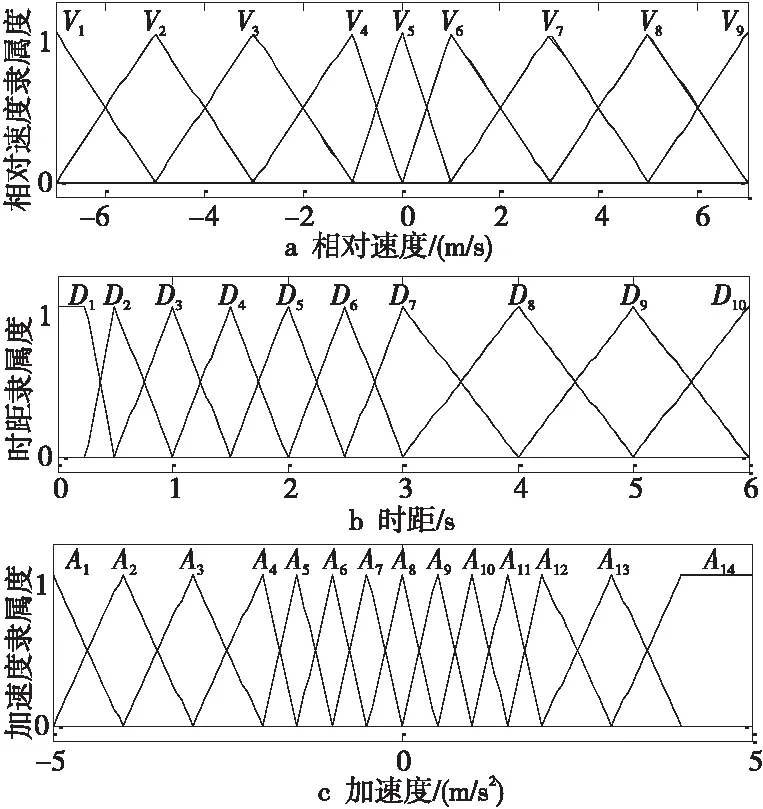
Figure 9 Membership functions of all variables when encountering dynamic obstacles图9 遇动态障碍物时各变量的隶属度函数

根据人工驾驶经验，建立速度规划的模糊规则表如表4所示。确定语言变量最大隶属度对应的实数值集合分别为：

Δv={-7,-5,-3,-1,0,1,3,5,7},

τ={0.25,0.5,1,1.5,2,2.5,3,4,5,6},

a={-5,-4,-3,-2,-1.5,-1,-0.5,0,0.5,1,1.5,2,3,4}。

Table 4 Fuzzy rule table in dynamic obstacle scenes表4 遇动态障碍物场景的模糊规则表

提取每个模糊规则并转换为如表5所示的模糊规划模型的样本集合。以相对速度和时距作为输入，以加速度作为输出，则模糊规划模型如图10所示。同样地，将遇动态障碍物场景的模糊规划模型的规则转化为输入输出样本集合对，利用神经网络自学习的性能，离线修正模糊规划模型，修正后的模糊神经网络规划模型如图11所示。

最后将模糊神经网络规划模型作为遇动态障碍物场景的速度规划模型，在线计算加速度。

4 仿真研究

仿真研究基于Matlab/Simulink展开，通过Matlab神经网络工具箱离线训练获得网络模型参数，在Simulink中建立速度规划仿真模型。

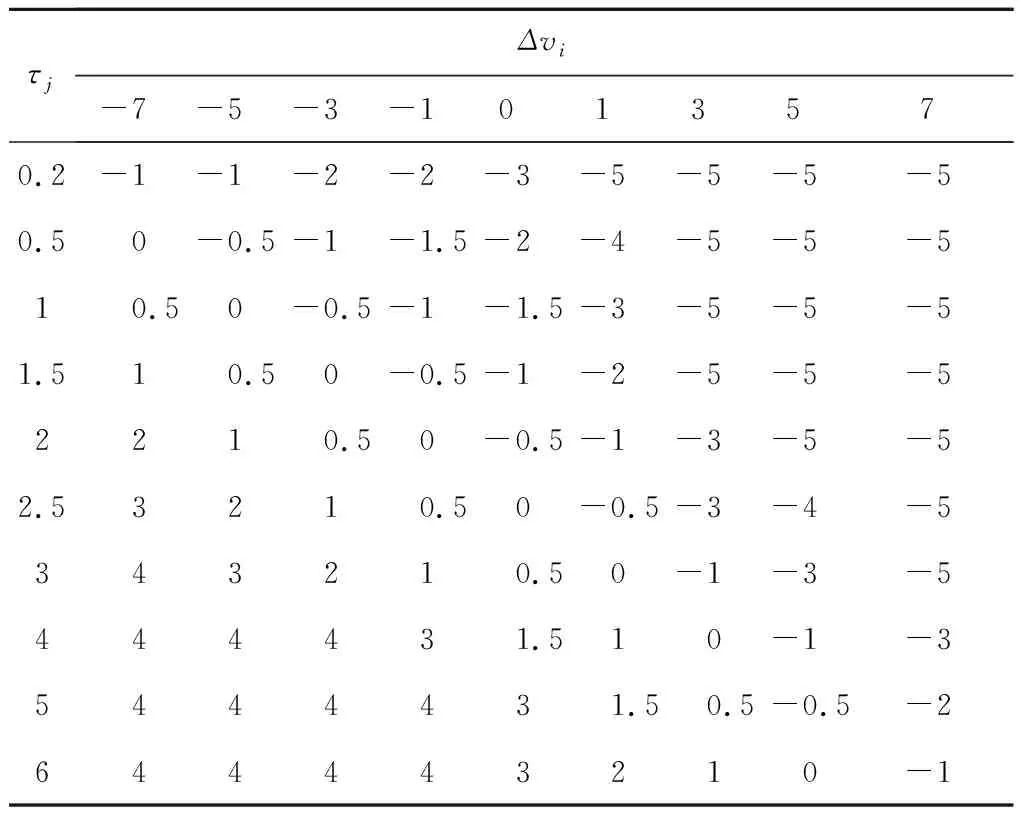
Table 5 Sample set a in dynamic obstacle scenes表5 遇动态障碍物场景的样本集合a

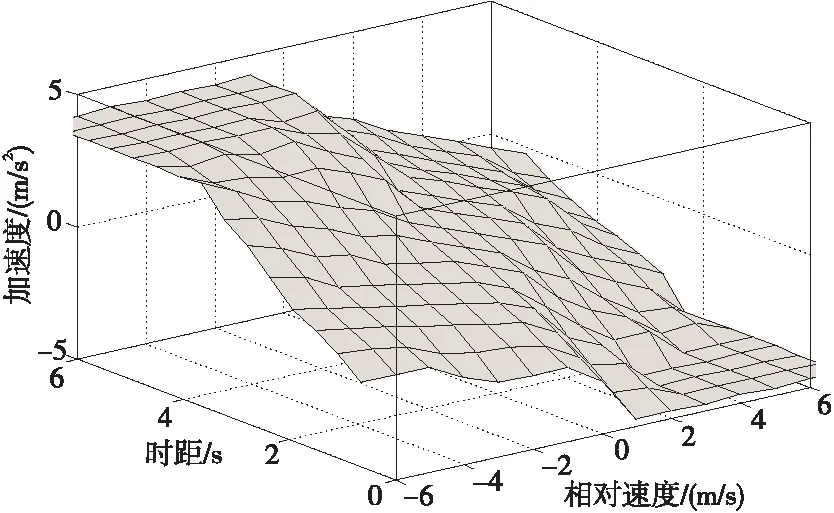
Figure 10 Fuzzy planning model in dynamic obstacle scenes图10 遇动态障碍物场景的模糊规划模型

Figure 11 Fuzzy neural network planning model in dynamic obstacle scenes图11 遇动态障碍物场景的模糊神经网络规划模型

4.1 遇静态障碍物场景仿真

遇静态障碍物场景，障碍物位于前方100 m处，自动驾驶车辆分别以20 m/s,15 m/s和10 m/s的初始速度开始驶向障碍物，测试车辆能否平滑降速。仿真结果如图12所示。

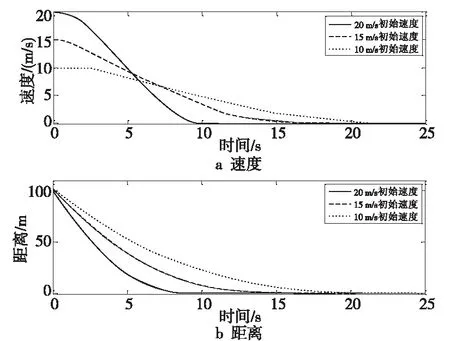
Figure 12 Decelerating test in static obstacle scenes图12 遇静态障碍物减速停车测试

由仿真结果可知，当自动驾驶车辆与障碍物距离小于6 s时距时，速度规划模块根据自车车速和到障碍物的距离计算输出减速度，车辆开始制动减速。结果表明，在不同的初始车速下，自动驾驶车辆都能够规划出连续平滑的减速度，实现车辆平稳降速。

本节分别采用模糊规划模型和模糊神经网络规划模型进行了对比实验。障碍物位于前方100 m处，自动驾驶车辆以15 m/s的初始速度开始减速，测试不同模型的性能。仿真结果如图13所示

Figure 13 Comparison test in static obstacle scenes图13 遇静态障碍物场景对比测试

相比于模糊规划模型，基于模糊神经网络规划模型生成的加速度曲线更加平滑，因而舒适性能更优。

考虑到自动驾驶系统中存在的各类扰动，如测量误差、执行误差和执行延时等，根据实际情况，本节在仿真系统中增加了扰动因素，以测试模糊神经网络速度规划方法的抗干扰性能。

仿真实验模拟的场景为：障碍物位于前方100 m处，自动驾驶车辆以15 m/s的初始速度开始减速。干扰因素为：速度测量加入了±1.5 m/s以内的随机误差，对距离测量加入了± 2 m以内的随机误差，执行系统的响应延时为0.5 s，制动系统的执行误差为±10%。仿真结果如图14所示，结果表明，在各类干扰因素影响下，车辆仍能保持平滑降速，规划的减速度仅在小范围内波动。

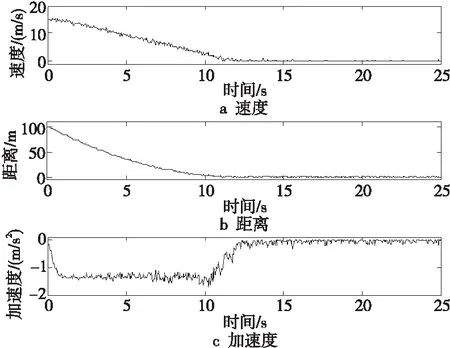
Figure 14 Anti-interference test in static obstacle scenes图14 遇静态障碍物场景抗干扰测试

以上仿真结果表明，基于模糊神经网络的速度规划模型，能够规划出较为连续平滑的加速度，有助于提升自动驾驶车辆在遇到静态障碍物时制动减速的舒适性。相比于模糊规划模型，其降速过程更加平稳，且具有一定的抗干扰能力，适应性强。

4.2 遇动态障碍物场景仿真

遇动态障碍物场景，前方车辆作为动态障碍物，且车速度随时间动态变化。自动驾驶车辆初始车速为15 m/s，到前车的初始距离为30 m，目标时距为2.5 s。本节分别进行了2类模拟测试：自动驾驶车辆跟随前车减速和自动驾驶车辆跟随前车连续变化。

对于自动驾驶车辆跟随前车减速的场景，假设前车从25 m/s恒速行驶，以-1.5 m/s2的减速度减速到10 m/s后保持恒速行驶；对于自动驾驶车辆跟随前车连续变化的场景，假设前车车速随时间以正弦函数变化。在上述2种场景中，测试自动驾驶车辆的跟车性能，仿真结果分别如图15和图16所示。结果表明，前车恒速行驶时(图15，0～40 s)，模糊神经网络模型能够规划连续平滑的加速度，使自动驾驶车辆保持与前车的2.5 s的跟车时距；前车从第1种恒速变化到第2种恒速运行时(图15，40～100 s)，自动驾驶车辆能够迅速响应前车的变化，并达到稳定跟车；当前车连续变化时(图16)，自动驾驶车辆能够较好地响应前车车速变化，跟车时距保持在2.5～3.0 s的合理安全范围内。

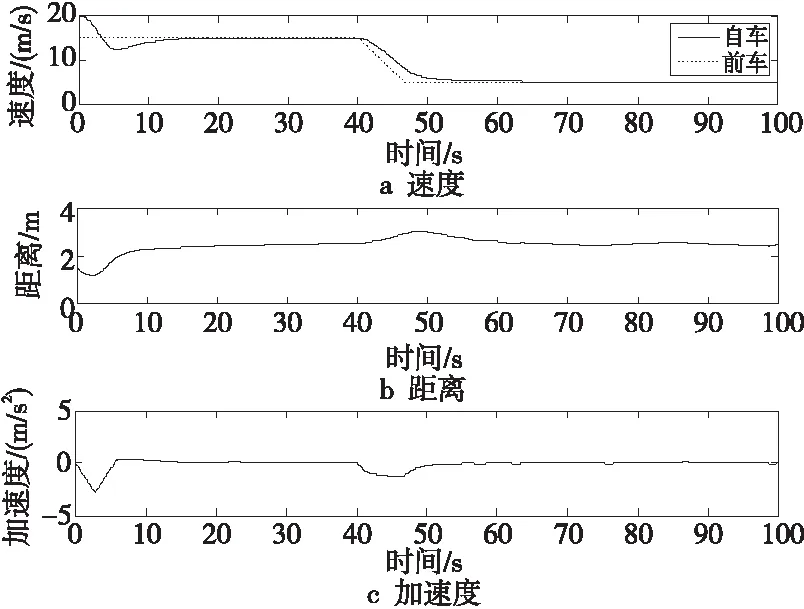
Figure 15 Test of slowing down with object vehicle图15 跟随前车减速测试

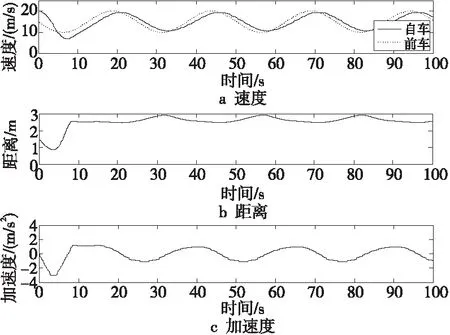
Figure 16 Test of varying with object vehicle图16 跟随前车连续变化测试

本节分别采用模糊规划模型和模糊神经网络规划模型进行了对比实验，前车速度随时间以正弦函数变化，以测试不同模型的性能。仿真结果如图17所示，采用基于模糊神经网络的速度规划模型生成的加速度曲线更加平滑，因而舒适性能更优。

Figure 17 Comparison test in dynamic obstacle scenes图17 遇动态障碍物场景对比测试

同样地，为检验模糊神经网络速度规划方法的抗干扰性能，本节对自动驾驶系统加入干扰因素。对速度测量加入了±1.5 m/s以内的随机误差，对距离测量加入了± 2 m以内的随机误差，执行系统的响应延时为0.5 s，制动系统的执行误差为±10%。仿真结果如图18所示。结果表明，自动驾驶车辆仍能保持较为稳定的跟车，加速度仅在小范围内波动。与图16(无干扰情况)相比，跟车时距在第10 s有明显的上升，主要原因是执行系统的响应延时干扰，加速或减速的时延造成车距急剧增大或减小。

Figure 18 Anti-interference test in dynamic obstacle scenes图18 遇动态障碍物场景抗干扰测试

以上仿真结果表明，基于模糊神经网络的速度规划模型，能够规划出连续平滑的加速度，实现自动驾驶车辆在遇到动态障碍物时，较好地跟随动态障碍物的变化，保持合理的跟车时距。相比于模糊规划模型，其舒适性能更优，且具有一定的抗干扰能力，适应性强。

5 结束语

本文将自动驾驶场景归纳为遇静态障碍物场景和遇动态障碍物场景，提出了基于模糊神经网络的速度规划方法，相比于传统的速度规划方法，本文所提出的速度规划方法的突出优点在于仅需简单的在线计算，因而计算时耗极低、工程实现简单，有助于提升自动驾驶系统的稳定性。同时，仿真研究结果表明本文速度规划方法提升了驾驶的舒适性，具有一定的抗干扰能力，适应性强。

在后续的研究中，将会基于模糊神经网络速度规划方法，对其它常见场景设计相应的速度规划模型并检验其适用性。同时，模糊神经网络速度规划方法在自动驾驶实车上的测试验证也将是下一步的研究工作。