站用电切换中调相机循泵电机的瞬态分析*

张玉良, 马宏忠, 蒋梦瑶, 刘一丹

(1.河海大学 能源与电气学院,江苏 南京 211100;2.国网江苏省电力有限公司 检修分公司,江苏 南京 211106)

0 引 言

中国现阶段的交直流混联电网已经实现了巨大的发展，尤其是特高压(UHV)直流输电，其电压等级和规模均已达到世界前列，打破了中国经济能源分布不均的格局[1-2]。然而UHV变电站交直流的并列运行易使其换流站直流端的电压支撑不足，新能源的汇集接入和电力大规模的外送极有可能导致系统过电压以及换相失败等故障。为解决换流站电压调节能力不足的问题，换流站配置了大容量调相机进行无功调节[3-5]。

目前在运行的大容量调相机一般是双水内冷式，其冷却系统延伸到机组外，由大功率380 V低压异步电机带动多组水泵进行循环冷却。站用电系统则是由多组站用变压器、380 V低压配电屏、交流供电网络、动力电及生活用电等用电设备构成[6-7]。站用电对于UHV变电站是非常重要的基础设施，保证了变电站各项设备的稳定工作。

变电站会对站用电进行定期检修，并做站用电双电源切换以及备自投的试验[8-10]。然而在站用电的切换过程中，不可避免地存在短暂的失电时间，当重新上电时，再次投入的电网电压与异步电机残余电压的相位和幅值的差异，极易导致异步电机中出现巨大的冲击电流，引发系统多级跳闸，若不能及时合闸，则会导致调相机过热，出现严重故障。

目前国内外对于异步电机重新投入使用的大部分研究将重点放在了电机起动和备自投的应用中，而对于双电源切换的研究较少。文献[11]通过建立dq坐标系下的动态数学模型对电机断电及重合闸过程进行了仿真分析，但尚未细致分析失电残压和相位信息，且需要复杂的数值计算。文献[12]利用频差和相位差提出了一种同步调相机的并网策略，但该方法对异步电机却不适用。

由交流电机的基本原理可知[13-15]，异步电机的定转子磁场在其正常运行时相对静止，旋转磁场与转子内电流相互作用，形成电磁转矩，转子则以转差率s相对其运动。在系统电源切换过程中，由于开关切换的物理性质，会有短时间的断电情况存在。异步电机的定子磁场会由于断电而突然消失，其转子中的感应电流在三相电断开的瞬间也会变为续流电流，并逐步衰减直至消失。按能量方向理解，则是在转子电感中存储的能量，断电后在回路中渐渐消散。电机转子中衰减的电流感应出衰变的旋转磁场，定子绕组中则感应出电压，并随着时间逐步衰减。

双电源切换过程中，在电机重新上电时其机端电压是电机失电后残余电压与电源电压的向量差，该值将直接影响冲击电流的大小[16]。本文对双电源切换时三相异步电机失电和重合闸的瞬态特性进行了仿真计算，发现了冲击电流随时间的变化规律，其最大值与最小值分别略滞后于相位相反和相位相同的点，由此提出了一种基于失电残压和电源电压幅值差的切换方法，并建立相关模型对其进行了分析。

1 失电残压

电源切换时在断电的瞬间，异步电机三相电源消失，其定子电流应该突降至零值，旋转磁势也应该突降至零值，但异步电机转子绕组是闭合回路，其磁通不能产生突变，因此在转子绕组回路中将会出现感应电流，以平衡由于定子电流突变而导致的磁通变化。该续流电流是直流性质的，并且会跟随转子绕组的时间常数进行较为缓慢的衰减。转子与其绕组中电流生成的旋转磁场相对静止，该旋转磁场相对于定子则以ωr的转速旋转。电机失电后转速会不断下降，转子绕组中的续流电流也会不断减小，而定子绕组中的感应电势即为失电残压，并以(1-s)ω0的角速度在持续衰减。

以三相异步电机的理想模型为基础，其定子电压可表示如下：

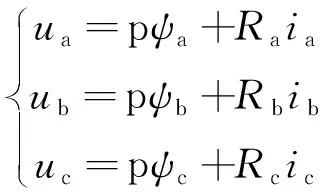
(1)

式中：ψa、ψb、ψc为异步电机定子绕组的磁链；p为对时间的微分；Ra、Rb、Rc为定子电阻；ia、ib、ic为定子电流。

异步电机的线电压则可以表示为

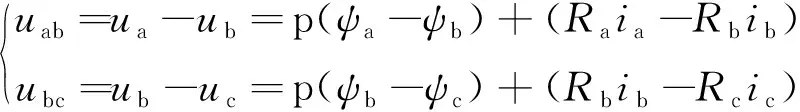
(2)

电机定子和转子绕组电流以及转速等信息均会在失电的瞬间存留，而在电机失电后，其定子电流会降至零。因此，在电机失电的瞬间可以由磁链守恒得到推导式如下：

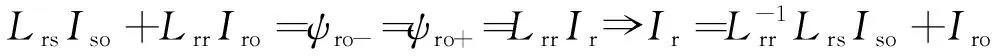
(3)

式中：Iso为电机失电前定子电流；Iro为电机失电前转子电流；Ir为电机失电后转子电流；Lrs为定子电感；Lrr为转子电感；ψro-为电机失电瞬间前的磁链；ψro+为电机失电瞬间后的磁链。

在异步电机失电后，式(1)、式(2)变为

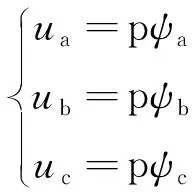
(4)

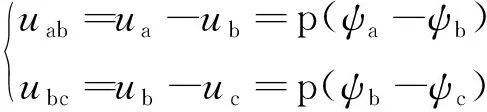
(5)

其中，电机定子磁链在失电后变为

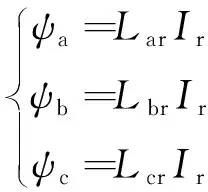
(6)

式中：Lar、Lbr、Lcr为定子三相电感。

根据电机转子绕组电压为零可以得到

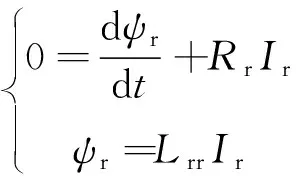
(7)

式中：ψr为转子绕组的磁链；Rr为转子电阻。

结合式(4)、式(6)可以得到

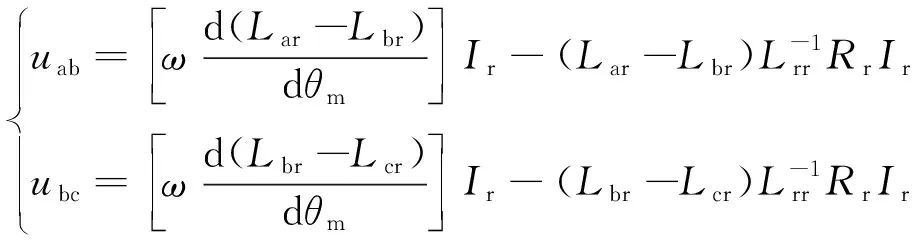
(8)

式中：ω为电机定子电压的角频率；θm为转子和定子同相轴线之间的夹角，即电角度。

本文以泰州UHV变电站调相机循泵电机IEC60034作为站用电切换时的研究对象进行相关计算仿真，其基本参数如表1所示。

表1 循泵电机参数

根据表1参数可对三相异步电机失电后的残压波形进行仿真，如图1所示。图1中，3 s时电机开始失电。根据图1，电机失电后定子电压是不断衰减的正弦波，其幅值和频率均在持续减小。

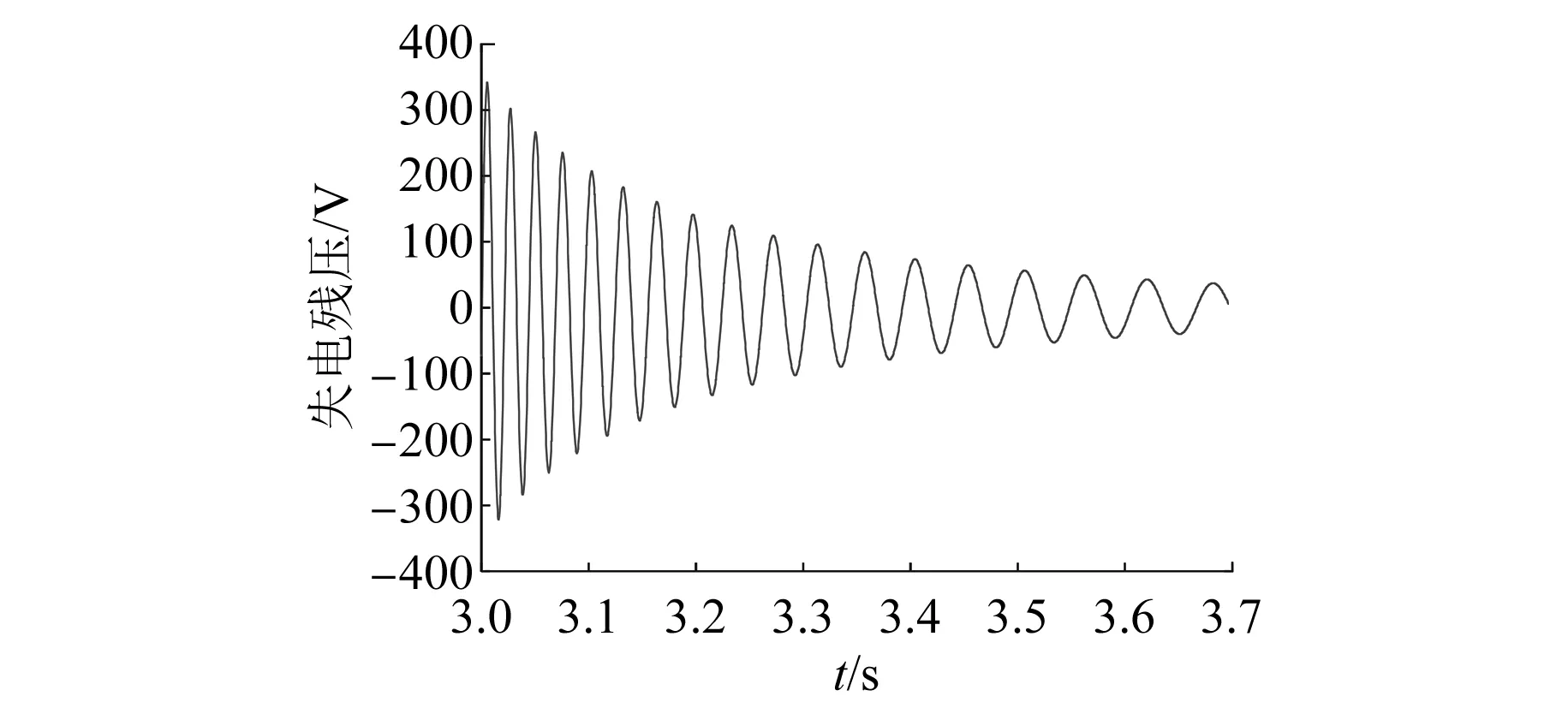
图1 循泵电机失电定子电压波形

2 重合闸的瞬态分析

由上文可知，在三相异步电机失电后的一段时间内定子绕组上的残压会一直存在，无法忽略。而电机失电残压的幅值变化与持续时间还与负载大小和电源切换时间有关。因此，需要在有失电残压的情况下，对三相异步电机重合闸[17-21]的瞬态进行研究。

假设电机在重新上电时定子端的残压存在且为us0，磁链ψr0以ωr的转速相对于定子旋转并持续衰减，转子绕组中的续流电流Ir0同样在持续衰减。

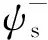
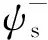
在定子回路中生成交流分量iss3，其衰减的时间常数为Tr。上述磁场的相互作用可由图2阐释。

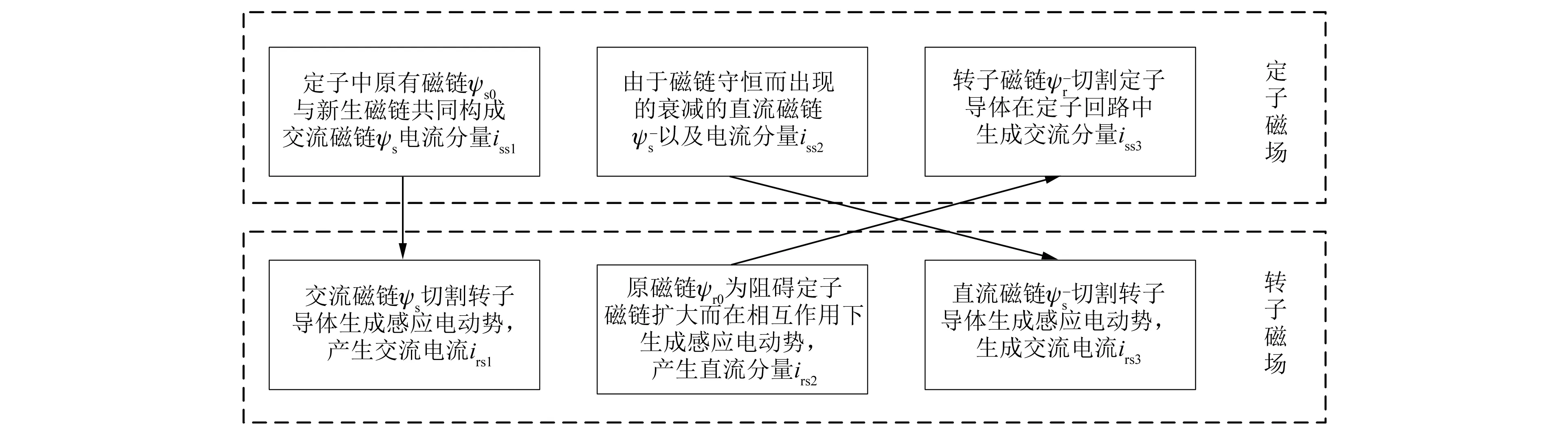
图2 电机重合闸时电磁场相互作用

基于定子磁链、转子磁链以及电压方程，利用状态空间建模法，对三相异步电机进行数学建模：

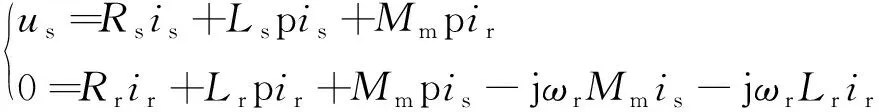
(9)

式中：us为电机定子电压；is为定子电流；ir为转子电流；Rs为定子电阻；Rr为转子电阻；Ls为定子自感；Lr为转子自感；Mm为电机互感；ωr为转子的角速度。

对式(9)进行拉氏变换并整理可以得到:

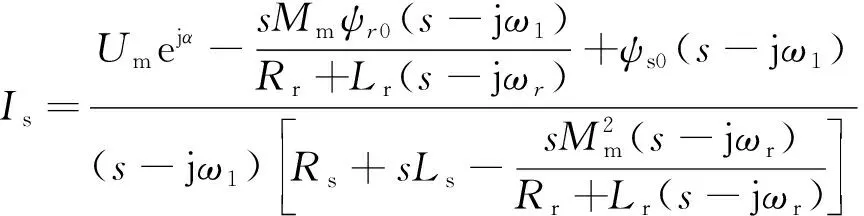
(10)

(11)

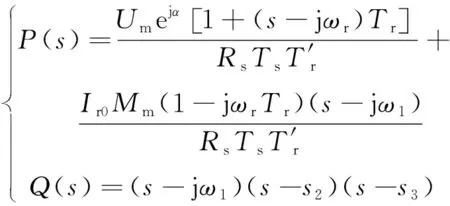
(12)

式(12)的分母为三次方程，即Q(s)有3个根，故可以发现s1=jω1。解上述等式式(2)，可得定子电流is在向量空间中的解:

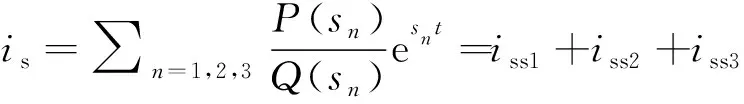
(13)

将式(12)的结果取拉氏变换后结合式(8)可得：

is=iss1+iss2+iss3=

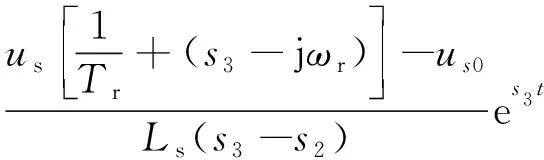
(14)

由上述解析式式(14)可以发现，电机失电后的残压us0和电源电压的幅值差主要影响衰减的定子电流中交、直流分量，因此整体上在电机重合闸瞬间总的定子电流会有较大的变化，即当失电残压与电源电压幅值差较大时，总的定子电流会大幅增加。

3 瞬态过程仿真

3.1 仿真模型

通过异步电机的结构、材料等参数利用多回路计算出电机各项电抗参数，构建出电机模型，并搭建站用电切换系统模型，如图3所示。

图3中系统模型整体分为电网侧、软起动模型、三相异步电机模型3部分。其中三相异步电机模型由前文所述各项参数构建，软起动模型则由控制模块、触发器模块、双向晶闸管模块构成。同步电压和阶跃起动信号分别经过控制模块和触发器模块产生6路触发脉冲，控制晶闸管向电机端的输出，以模拟循泵电机软起动器[22-23]。

图3 站用电切换系统模型

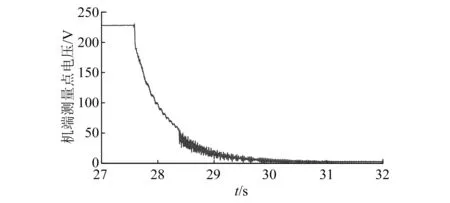
图4 循泵电机实测惰走曲线

3.2 冲击电流随时间变化规律

以站用电切换时间为0.1 s为例进行仿真，待电机起动稳定运行后，在3 s时将三相断路器断开，并于3.1 s时将软起动模型接入，以此观察重合闸时的冲击电流。仿真结果如图5所示。

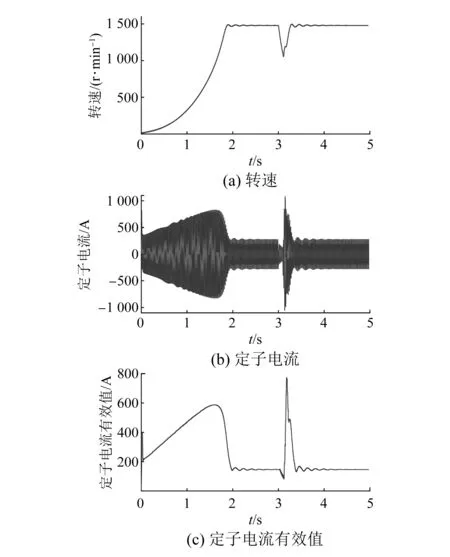
图5 电源切换时间为0.1 s时仿真波形

当电源切换时间为0.1 s时，冲击电流最大为1 079 A，达额定电流7.6倍，已经远高于软起动时的最大电流。同时对不同的电源切换时间进行仿真，统计结果如表2所示。

为了保持每次仿真时重合闸时电源电压均为同相位，选取0.02 s为最小时间间隔。从表2可以发现，冲击电流分两个阶段变化：第一阶段是电源切换时间为0.02～0.06 s时，冲击电流有短暂的增长；第二阶段是0.06 s以后，冲击电流开始降低，并随时间推移而降速变缓。

表2 不同切换时间的冲击电流

对于第一阶段的变化，根据图1，电机失电残压与电源电压的幅值差在随时间逐步扩大。因此在最开始的几个周期内，由于失电残压的幅值在逐步减小，电源电压与失电残压的幅值差不断扩大，冲击电流会持续增长。根据图1，从3 s失电到3.06 s，失电残压的周期仅增加了0.002 s，而幅值从380 V降至265 V，下降了115 V，可以忽略频率的微小变化，认为仅幅值在发生变化；根据表2，切换时间从0.02 s至0.06 s时，冲击电流增加了729 A，与前文式(14)得出的结论一致，即失电残压与电源电压的幅值差对冲击电流的影响占主要地位。

第二阶段中从0.06 s至0.10 s，电机失电后转速和电压均下降较快，冲击电流因此也有大幅下降。从0.1 s至0.3 s，电机转速下降稍缓，但已明显下降，且负载转矩较大，因此重合闸时为了提供足够的转矩，软起动器会将电压保持较高的状态，冲击电流下降较缓。而0.5 s以后电机转速已下降过半，软起动器在接入瞬间提供的电压不会达到峰值，并随转速的下降速度持续降低，因此冲击电流下降略快，并开始低于软起动时的最大电流。

3.3 基于幅值差的切换方法

将三相异步电机模型负载调整为类水泵负载后，令电机在0 s时起动，稳定运行后断开电源，并在不同时刻重新接入软起动模型。通过ode23t算法仿真获取电机断电后残压和重新接入软起动器时的电源电压及相位等信息，作出图6所示失电残压与电源电压幅值差关系图。

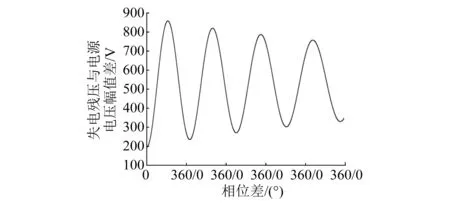
图6 失电残压与电源电压幅值差关系

三相异步电机在失电后，残压的幅值与频率均在持续减小，失电残压与电源电压相位差和幅值差也在持续变化。根据图6，失电残压与电源电压幅值差的最大值为二者第一次相位差达191.34°时，即滞后相位相反的点10°左右。类似地，电压幅值差最小值出现在滞后相位相同的点10°左右。但随着时间的推移，电压幅值差出现极大极小值点的相位差会逐渐滞后并扩大，如第二次极大值出现在二者相位差约为235°时，极小值出现在二者相位差约为91°时。这个滞后的量取决于失电残压衰减的快慢，衰减越快则频率越小，即该滞后的量越大。

冲击电流的大小主要取决于失电残压和电源电压的幅值差，而冲击电流的最小值点略滞后于相位相同的点，因此可以选择失电残压与电源电压幅值差最小的时刻进行重合闸操作，以减小冲击电流并获得较为理想的瞬态转矩。

目前变电站中对于电机断电后重合闸主要有直接重合闸、检同期、启用备自投等3种常用方法。

直接重合闸即是在系统断电后立即进行重合闸操作，在变电站站用电系统中体现为双电源装置的自动切换，但限于设备的硬件性能特性，一般需要300～1 000 ms完成重合闸动作。根据表2的仿真结果，在这一时间段内进行重合闸操作会产生极大的冲击电流，极易致使保护设备动作。

检同期合闸主要是针对两侧电压幅值基本相同的设备，找寻失电残压和电源电压相位相同的点进行重合闸操作。根据上述仿真结果，三相异步电机的失电残压幅值是持续衰减的，又因为其频率也在持续衰减，导致二者幅值差的极大值点和极小值点分别滞后于相位相反和相同的点。因此，该方法对调相机循泵电机存在较大误差且成本较高。

启用备自投是延长双电源切换时间，让备自投开始运行，待主设备完全停机后，再从备用设备切换回主设备，让主设备重新起动。该方法虽不会引起保护设备动作，但让系统整体恢复正常状态需要较长的时间，甚至会导致调相机因过热而出现故障。

综上所述，目前常用的3种方法均存在不足，因此本文提出基于失电残压和电源电压幅值差的切换方法，可以在尽可能降低冲击电流的同时快速进行重合闸操作。

根据冲击电流的变化规律，本文提出如下降低站用电切换失败概率的建议，供维护设计人员参考。

(1) 由于重合闸后短暂的时间内冲击电流会随两侧的频差和角差的增大而增大，因此如若电源开关水平较高(10 ms级)，则可以直接投切，不会产生过大的冲击电流。

(2) 重合闸后在一定的时间后，冲击电流会随着时间逐步降低，但由于软起动器的特性，当反向转矩依然在一定范围内时，为提供足够的起动转矩，冲击电流会大于正常起动电流。因此，当开关水平较低时，应适当延长电源切换时间，直至冲击电流低于电机正常起动最大电流，从而保证站用电切换过程不会出现多级跳闸的情况。

(3) 可以根据失电残压与电源电压幅值差来判定重合闸时刻，在该幅值差达到最小值时再进行投切操作。

4 结 语

在变电站站用电切换的过程中，在循泵电机失电后，转子电流不会突变，定子绕组中则会感应出失电残压，且该残压的频率和幅值持续衰减。因此，电机失电后重合闸的瞬间会产生较大的冲击电流。本文针对该问题对电源切换过程中失电和重合闸的瞬态进行分析，发现了最大冲击电流根据电机失电时间长短，先短暂增长再持续减小的规律，且冲击电流的最大值滞后于相位相反的点，该滞后的量由失电残压衰变的速率决定，因此可以根据失电残压和电源电压的幅值差来确定投切的时刻。