磁悬浮平台直线同步电动机TS型模糊控制的研究*

张玉涵, 蓝益鹏

(沈阳工业大学 电气工程学院，辽宁 沈阳 110870)

0 引 言

采用直线电动机进行驱动的数控机床具有结构简单、响应速度快等优点，但导轨与平台直接接触不可避免地存在摩擦[1]，为消除直线电动机数控机床的非线性摩擦，提高数控机床的控制精度和运行稳定性，采用直线磁悬浮同步电动机(LMSSM)对数控机床运动平台进行驱动[2-3]。LMSSM产生的电磁推力驱动平台进行水平方向运动，竖直方向的磁悬浮力抵消平台重力，使平台稳定悬浮，实现了无摩擦进给[4]，消除了摩擦扰动，提高了高精度数控机床伺服系统的性能[5-6]。

无摩擦机床磁悬浮平台使用的LMSSM系统是一个非线性系统，且具有强耦合性，故在复杂的工业生产条件下，往往无法得到精确的数学模型，LMSSM的数学模型只在理想状态下才能够表示真实的系统，这就要求，所使用的控制方法不能过于依赖数学模型。因为LMSSM进给系统与磁悬浮系统之间共用气隙磁场，所以存在电磁耦合现象，而且存在磁路饱和、磁滞和不同悬浮高度下参数时变问题。由于使用LMSSM直接对机床进行驱动，导致负载及多种不确定扰动直接作用于电动机，影响系统的控制性能。

为解决上述问题，需要选择一种合适的控制方法对LMSSM进行控制，发挥其直接驱动的优势，模糊控制由于不需要被控对象精确的数学模型，成为了控制LMSSM、使其发挥直接驱动优势的选择之一。但是，对于LMSSM系统这样的多维系统，通常需要定义多个语言变量，才能获得满意的控制效果，而这就需要大量模糊规则进行控制，而由于规则之间存在耦合作用，对某一条规则的修改会给整个模糊控制器带来难以控制的影响，增大了控制器调试难度，这就导致了传统的Mamdani型模糊控制器不能满足系统的控制需求。

本文设计了一种基于TS(Takagi-Sugeno)模型的模糊控制器。为了描述复杂的非线性系统，1985年，Takagi和Sugeno通过研究，提出了一种TS模糊模型[7]。TS模型的几何思想是用多个小线段表示一条曲线，换言之就是用多个线性系统的组合表示一个非线性系统，即以规则的形式把整体非线性系统表示成许多局部线性子系统，然后将这些局部线性子系统通过隶属函数连接起来。而TS模糊控制器就是根据这种思想设计的。其后件部分用函数的线性组合取代了传统的Mamdani型模糊控制器输出的语言变量，因此，基于TS模型的模糊控制器在控制效果相近的情况下，与传统模糊控制器相比，模糊规则数显著减少，设计难度也大大降低，对控制器的修改更加方便，更能适应复杂的控制要求。该控制器具有结构简单、运行稳定、抗扰能力强等特点，可以满足一般的控制需求。

1 LMSSM运行原理及数学模型

1.1 LMSSM的运行原理

磁悬浮进给平台结构如图1所示。LMSSM的定子以及辅助结构位于机床的磁悬浮平台，而负责进给的运动平台包括电动机动子、电涡流传感器等结构。在磁悬浮进给平台稳定工作时，平台与导轨之间存在一定空间，因而避免了摩擦的产生。

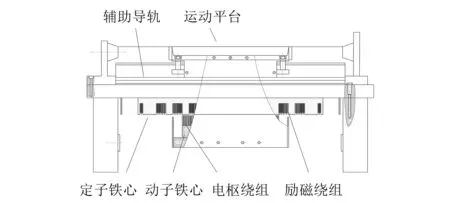
图1 磁悬浮平台结构图

本文所设计的控制器控制的是驱动机床的LMSSM，是在旋转电机的不断演变下形成的，为磁悬浮平台提供水平驱动力和悬浮力的，确保平台稳定运行[8]。向缠绕在电动机的定子上的励磁绕组中通入直流电后，会在气隙中产生磁场，称为励磁磁场。向磁悬浮电动机动子上的电枢绕组通入三相交流电后，会产生按正弦波形状改变并沿水平方向行进的行波磁场。行波磁场和励磁磁场相互作用产生作用力，推动进给平台，使其在水平方向运行。而在垂直方向上存在与重力大小相等、方向相反的麦克斯韦力，在其作用下，动子稳定悬浮。

1.2 LMSSM的数学模型

为了简化电动机的数学模型，假设如下条件[9-10]：

(1)忽略电动机的铁心饱和，电动机磁路为线性；

(2)忽略直线电动机的端部效应；

(3)忽略铁心的涡流与磁滞损耗；

(4)认为通入电动机电枢绕组的为三相对称正弦交流电；

(5)电动机磁极上不含阻尼。

根据以上假设，可以推导出LMSSM在d-q轴下的电压方程、磁链方程、推力及悬浮力方程和运动方程[11-12]。

电压方程：

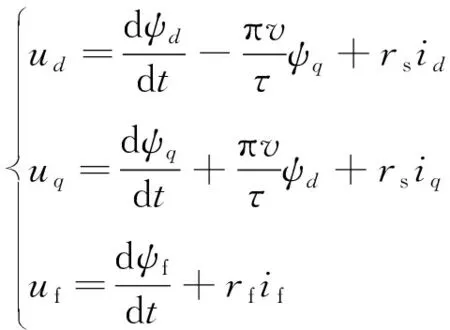
(1)

磁链方程：

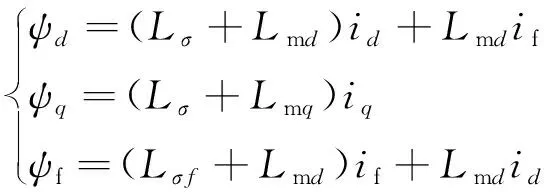
(2)

式中：ud、uq为电枢绕组d轴、q轴端电压分量;uf为励磁电压折算到定子的值；ψd、ψq为d轴、q轴的磁链;ψf磁极磁链分量；v为动子运动速度，且v=2fτ，f为电源频率;rs为电枢绕组电阻；rf为磁极励磁绕组折算到定子的电阻;id、iq为电枢绕组d轴、q轴电流分量;if为励磁电流折算到定子的值；Lσ为电枢绕组漏感；Lmd、Lmq为d轴和q轴的主电感。

推力方程：

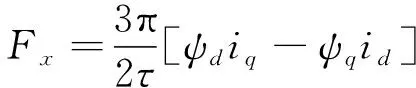
(3)

水平方向运动方程：

(4)

悬浮力方程：

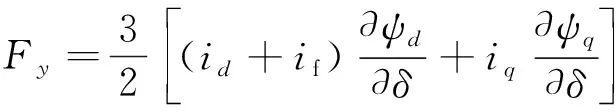
(5)

垂直方向的运动方程：

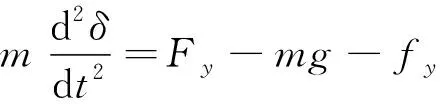
(6)

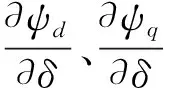
采用id=0的控制，此时，d轴上只存在励磁绕组的励磁磁场。推力、悬浮力表达式简化为[13]

(7)

(8)

2 TS型模糊控制器的设计

2.1 控制系统构成

根据LMSSM的数学模型[14]并考虑模糊控制的特点及控制原理，系统的速度环采用基于TS模糊模型的模糊控制器，系统框图如图2所示。

图2 LMSSM双闭环控制系统框图

2.2 控制器的设计

一般的模糊控制器设计分为，隶属度函数的选择、模糊规则的设定以及选择适当的清晰化方法等。因为TS型模糊控制器的输出是函数的线性组合，所以不需要清晰化方法。本文所研究的模糊控制器是基于MATLAB软件的GUI图形界面进行设计的。

本文设计的TS型模糊控制器以误差e和误差的变化率ec为输入，分别表示电机实际速度与给定运行速度的差及该值的变化率，以q轴电流iq为输出。本文控制器所控制的LMSSM运行速度范围大约为0～1 m/s左右，通过调整因子将速度误差e和速度误差变化率ec转换到模糊论域[-3，3]上，为减少模糊规则数量，简化控制器，则取输入：N(负)、Z(零)、P(正)。则误差和误差的变化率模糊子集均取为{N、Z、P}。

根据经验，在e较大时，使用的隶属度函数应较陡，在e较小甚至趋近于零时，应使用平缓的、甚至斜率为零的隶属度函数，因此，本文设计的控制器在论域两端使用灵敏度较高的三角形隶属度函数，在趋近于零的位置使用梯形函数，以此获得较为优越的控制效果。输入量e、ec的隶属度函数在MATLAB界面下如图3所示。

图3 系统输入的隶属度函数

传统模糊控制器的规则，一般由前人的经验积累得到，数量一般为输入量语言变量的排列组合。但是，随着电动机种类的更新以及控制环境的不断变化，前人的经验有时不能适应控制需求，过多的规则数量也会造成控制器过于复杂，难以修改优化等问题。而TS型模糊控制器的规则不会过分依赖前人经验，可以根据推导或计算得出，更容易满足不同情况下的个性化控制需求，且减少了规则的数量，控制器更易于设计和优化。

令Ri表示模糊系统的第i条规则，TS模糊控制器模糊规则形式如下：

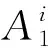
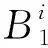
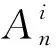
本文设计的控制器使用加权平均法求得系统输出，故系统的输出为

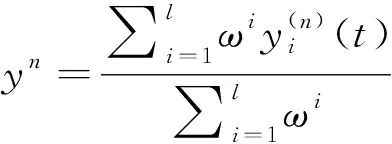
(9)

式中:ωi是第i条模糊规则的适用度,

建立TS模糊模型，需要大量的输入输出数据，进行分析辨识，找出系统局部线性的特点，将系统分段描述。本文需要使用TS模型描述控制器，因此先给出理想状态下输出量的响应曲线，然后根据控制的不同阶段输入不同语言变量时，如何使输出量尽量贴合理想状态下的输出响应曲线，确定每组输入量所对应的输出量。经过对大量数据的分析(先确定其局部线性特征，再使用最小二乘法等数学方法计算出描述这一线性特征的函数)，得出如下4条模糊规则：

R1:ifeisN

thenu=e+1

R2:ifeisZandecisN

thenu=-0.1e+4ec+1.2

R3:ifeisZandecisP

thenu=0.9e+0.7ec+9

R4:ifeisPandecisP

thenu=0.2e+0.1ec+0.2

控制器的模糊控制规则如图4所示。

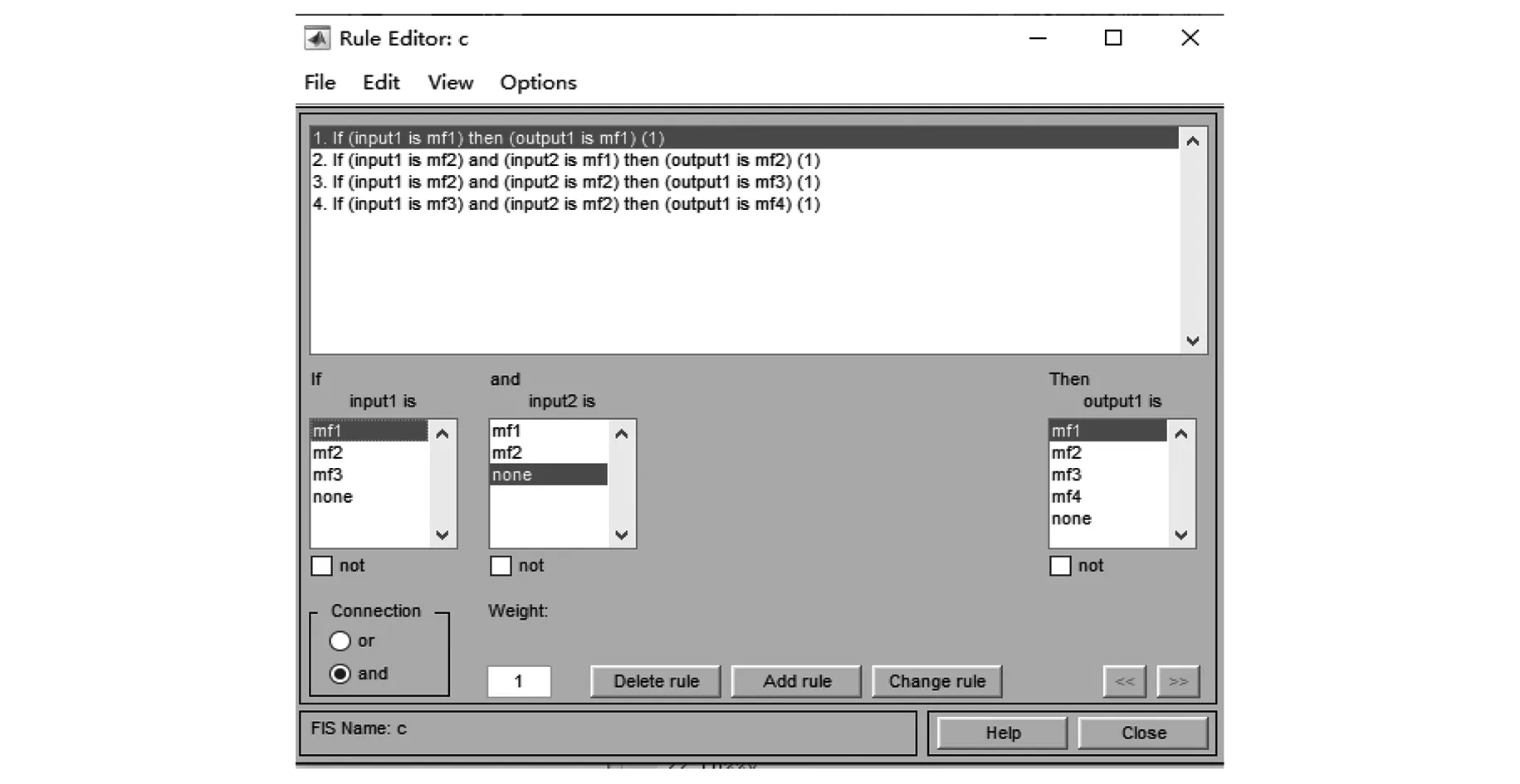
图4 控制器的模糊控制规则

基于MATLAB软件的模糊控制GUI界面，将控制规则和后件函数的系数分别输入rules和output界面，所设计的TS模糊控制器模糊推理图如图5所示，模糊推理三维图如图6所示。

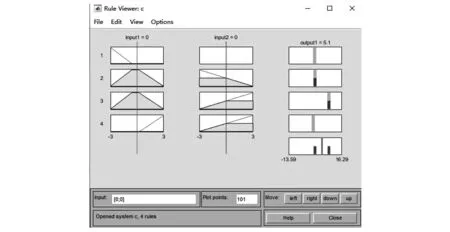
图5 控制器模糊推理过程图

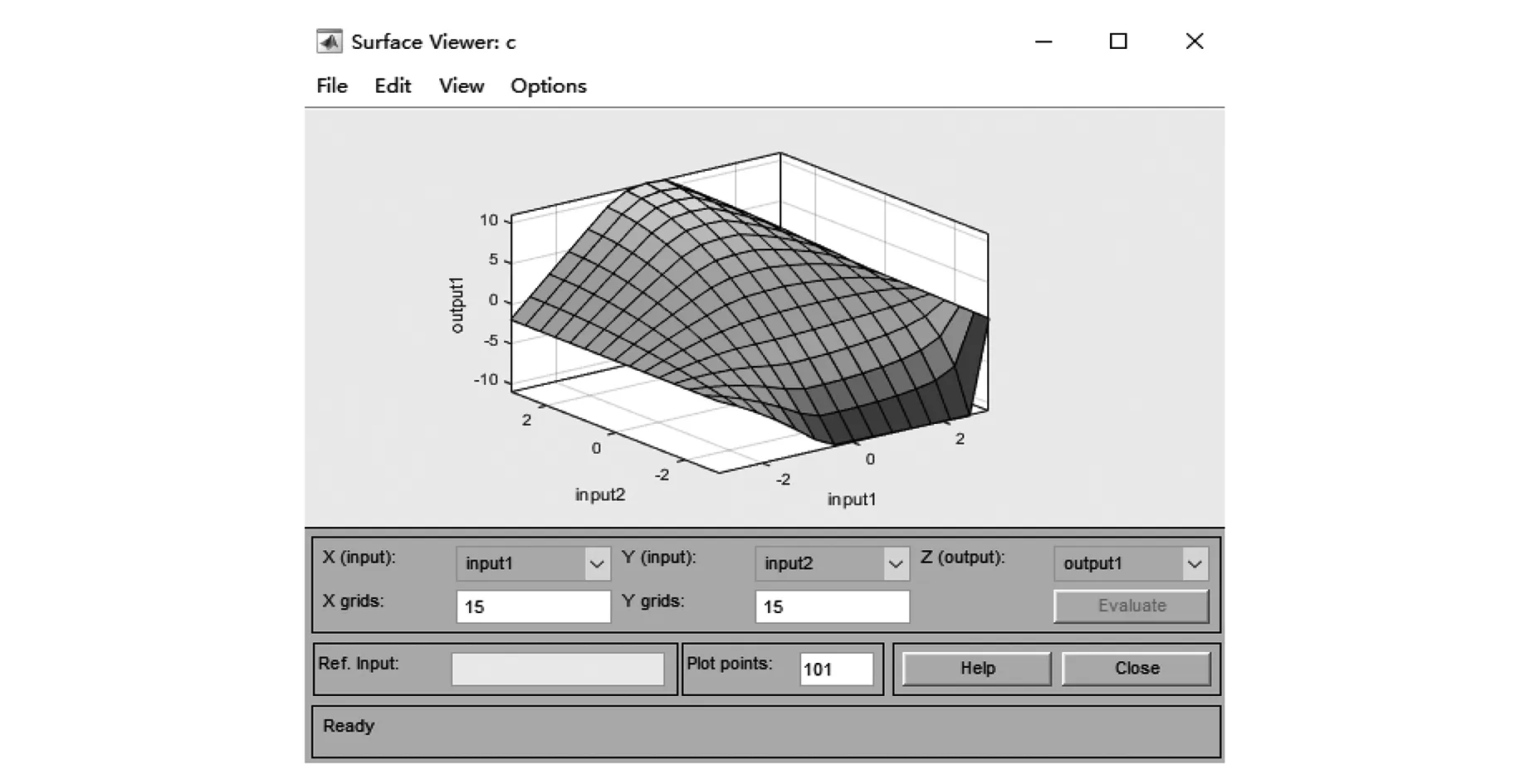
图6 模糊推理三维图

3 控制系统的仿真

3.1 控制系统仿真模型

根据图2所示的控制系统结构框图，搭建磁悬浮直线电动机TS模糊控制系统的Simulink仿真模型，将所设计的控制器搭载到工作空间中以便对电动机进行控制。仿真模型如图7所示。

图7 控制系统仿真模型图

仿真参数设置：dq轴电感Ld=Lq=0.018 74 H,d轴主电感Lmd=0.009 5 H，电阻Rs=1.2 Ω，极距τ=0.048 m，极对数p=3，电机动子及平台质量M=10 kg；励磁电流if=5 A。

3.2 仿真结果研究

将磁悬浮运动平台的水平进给速度，即LMSSM运行速度给定值设置为1 m/s，当0.1 s时，加100 N的负载，得到的推力、速度响应曲线,分别如图8、图9所示。

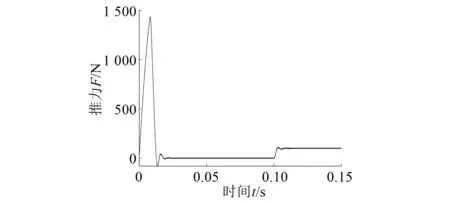
图8 推力响应曲线图

图9 速度响应曲线图

观察图8可知在起动阶段电动机的推力快速升高，驱动电动机进行加速运动，起始阶段如图9所示，直到达到稳态。空载阶段，平台无外力作用，故推力降为零。在0.1 s时，加100 N的负载，系统快速做出响应，推力升高为100 N以平衡负载。

从图9速度响应曲线可以看出，无论是空载情况下(0.06 s之前)还是负载情况下(0.06～0.10 s)，电动机均能够正常稳定运行，仅在0.1 s加入负载时有不超过0.01 m/s的速度降落，且在0.005 s内恢复。可见该控制系统快速性好、抗扰能力较强，在面对突然施加的负载或扰动时，反应速度较快，可以胜任大多数情况下的控制任务。

使用传统的PI控制器代替速度环上的TS模糊控制器，将二者的控制效果进行比较，得到推力、速度响应曲线对比图分别如图10、图11所示。

图10 PI控制器与TS模糊控制器推力响应曲线对比图

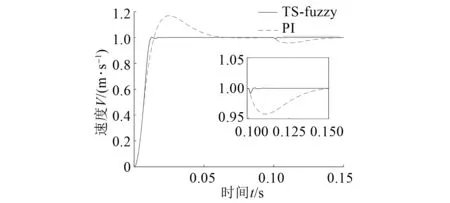
图11 PI控制器与TS模糊控制器速度响应曲线对比图

从速度响应曲线对比图中不难看出，在PI控制器的控制下，系统调节时间为0.058 s，超调量为17%，加负载时恢复时间为0.045 s，在TS模糊控制器的控制下，系统调节时间为0.012 s，几乎无超调，加负载时恢复时间为0.005 s，电动机响应速度更快，超调小，稳定性也较好。与PI控制器相比，TS模糊控制器控制性能优势明显。

同时作为模糊控制器，在相同条件下，TS模糊控制器的控制性能与传统的模糊控制器的控制性能相近，甚至优于后者，但是，本文设计的TS模糊控制器只需要4条模糊规则来实现控制，而在控制要求相同的情况下，传统的模糊控制器大都需要更多条规则来实现控制效果，而且其输出是语言变量，需要繁琐的清晰化过程，无形中增加了计算量。相比之下，本文设计的TS模糊控制器结构简单，占用CPU空间少，计算迅捷，显现出易于实现的优势。

4 结 语

(1) 研究LMSSM的运行原理，建立数学模型，并以此为依据，设计了LMSSM系统的TS模糊控制器。

(2) 通过MATLAB建立控制系统的仿真模型并进行仿真研究。在系统运行0.012 s后，电动机以给定速度1 m/s稳定运行，在0.1 s时施加100 N的负载，其恢复时间为0.005 s，然后运行速度恢复为给定速度1 m/s。仿真结果表明，该控制系统反应速度快，抗扰性强，控制效果好。

(3)使用PI控制器对电动机进行控制时，调节时间为0.058 s，才能以给定速度运行，施加负载后，需0.045 s后速度才能恢复。相比之下TS模糊控制器具有明显的性能优势，并且与传统模糊控制器相比，TS型模糊控制器使用了较少的模糊控制规则，结构更加简单，运行速度更快。