基于改进贝叶斯阈值的寻优去噪算法

余传本，刘增力

（昆明理工大学 信息工程与自动化学院，云南 昆明 650500）

0 引 言

在采集、获取、传输图像的过程中，由于电阻引起的热噪声、传输设备的不完善等各种因素的干扰，图像会不可避免地被噪声污染，这不仅影响用户对图像的视觉体验，也会影响对图像的后续处理。因此在对图像执行后续处理之前，必须先对图像进行去噪。常用的降噪方法有中值滤波、维纳滤波等[1-3]，但是在使用这些方法降噪时会丢失图像的细节部分。小波去噪方法克服了上述缺点，在一定程度上能够反映图像的细节[4]。

长期以来，人们对小波去噪进行了大量研究，包括基于小波模极大值降噪、基于小波系数相关性降噪以及基于小波阈值函数降噪。从最小均方误差的角度来看，小波阈值去噪方法原则上可以在获得更好视觉效果的前提下达到最佳的去噪效果而被广泛应用[5-7]。常用的阈值确定方法[8-10]有VisuShrink、SureShrink、BayesShrink以 及Feature Adaptive。VisuShrink去噪后的图像边缘比较清晰，细节等局部特征保留比较好，但不可避免地会对边缘小波系数产生过扼杀，产生伪吉布斯效应等视觉失真现象。SureShrink和BayesShrink去噪后的图像处理得比较平滑，但是边缘比较模糊，效果相 对较差。

本文在贝叶斯收缩降噪方法的基础上，提出一种改进的优化算法，即改进遗传算法自适应贝叶斯阈值优化算法。改进的方法基于多维变量进行阈值优化，以最低均方差（Mean Square Error，MSE）为优化目标，设计适应度函数进行计算。

1 贝叶斯小波阈值

假设信号为(fi,j,i=1,2,…,N,j=1,2,…,N)，N是2的幂，它被加性随机噪声εi,j污染，记为：

式中：εi,j是均值为零的独立同分布的正态分布，并且独立于fi,j。

令g=gi,j, f=fi,j, ε=εi,j，又令Y=Wg, X=Wf, V=Wε其中W表示二进正交小波算子。于是可得：

贝叶斯小波阈值是在广义高斯分布（Generalized Gaussian Distribution，GGD）模型中取得，该模型的建立基于统计观察，描述如下：

式中：-∞＜x＜∞, σx＞0, β＞0。α(σx, β)、C(σx, β)分别为：

对于σ2的估计，可由目前通用的中值估计法 得到：

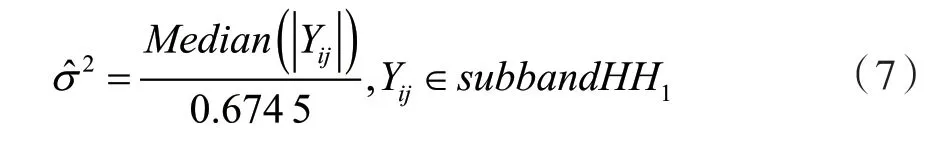
对于σx的估计，由于信号小波系数与噪声小波系数相互独立，所以由式（2）可得：

σ2Y

是Y的方差，又因为Y服从高斯分布，所以可得：

子带大小为n×n，所以由式（8）和式（9）可得σx的估计为：

于是可得最终的贝叶斯阈值函数为：

2 多变量改进遗传算法自适应贝叶斯阈值优化

当前的阈值只是全局的，无法灵活地对应不同的图像位置进行变化，针对这个问题，设计多变量自适应改进遗传算法阈值优化算法，对原Bayes算法的固定阈值进行不同情况的自适应变化，变量即为遗传算法种群[11-12]。因此，优化的自适应变量分别为：小波分解HVD的H、V、D高频分量计算阈值相乘的自适应系数xtH, xtV, xtD和小波分解HVD的H、V、D高频系数相乘的自适应系数xH, xV, xD。

根据以上优化思路以及自适应系数r可知优化的变量有7个。遗传算法种群population=(xtH, xtV, xtD, xH, xV, xD, r)为7维数组，定义域为[0,1]。

在优化问题中，混沌理论和混沌序列的产生越来越普遍，由于混沌易于实现且避免了陷入局部最优的特殊能力，因此作为一种新技术引起了广泛的关注。

本文使用混沌映射来生成混沌序列，而不是通过随机过程进行遗传算法，从而提高了算法效率。首先生成初始种群，其次计算个体的适应度函数，最后在遗传操作中执行选择、突变及交叉操作。所不同的是，它采取的是将混沌序列与遗传算法相结合的方法，在遗传算法的遗传运算、变异算子及交叉算子中，本文将使用逻辑函数生成的混沌序列来进行抓取。

2.1 混沌交叉

2.1.1 调整交叉操作的频率

在遗传算法的使用中，突变概率Pc通常是随机选择的，任何初始值x0，本文都可以使用x0作为准则，如果小于x0，则可以超过，否则它将不会被超过，如下所示：

式中：Pc是一个预选值，通常为0.9。

2.1.2 确定交点位置的混沌序列

设置L个长染色体，在区间(0,1)中随机选择一个数字xn作为初始值，并使用逻辑模型迭代生成混沌序列xn+1。利用公式C=(int)xn+1*L把序列xn+1映射染色体基因座空间，在该位置进行交叉操作，以便形成新的后代。只有少数点基因被替换，而不是片段连接，并且变化很小，避免了在生成后代时使用遗传算法。最佳缓冲问题出现在中等种群中，可以由混沌序列确定所有交叉点的位置。

2.2 混沌变异

（1）检查变异操作的频率。在遗传算法的使用中，突变概率Pm通常是随机选择的。方法与上面相同，其中Pm是预选值，通常为0.02。

（2）混沌顺序决定了突变点的位置，方法与混沌分频器相同。

基于上述混沌理论，本文提出的改进遗传算法的自适应贝叶斯阈值优化方法的步骤如下。

步骤1：随机产生一组具有7维变量（需要优化的7个参数）的初始个体以形成初始种群，并评估每个个体的适应度值。

步骤2：确保算法搜索关键参数的最优值，并评估是否满足算法的收敛准则（以最小的MSE为优化目标）。如果满足，则运行搜索结果；否则执行以下步骤。

步骤3：根据调整值的大小以一定方式进行复制操作。

步骤4：根据混沌交叉概率进行交叉操作。

步骤5：根据混沌变异概率进行变异运算。

步骤6：返回至步骤2。

3 实验仿真与分析

3.1 算法流程

整体的改进遗传算法自适应贝叶斯阈值优化方法流程及代码实现如图1所示。

图1 改进遗传算法自适应贝叶斯阈值优化方法

3.2 遗传算法结果分析

常用的图像质量评估参数为信噪比（Signal-Noise Ratio，SNR）和均方差（Mean Square Error，MSE），定义如下：

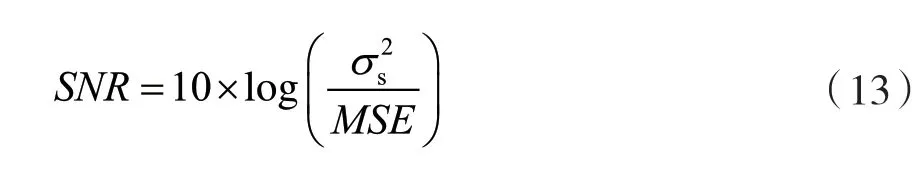
式中：M、N是图像的垂直和水平方向上的像素数，S(i, j)和S '(i, j)是原始图像以及去噪后图像在点(i, j)处的像素值。

本文选择了两张图片进行仿真实验，用于验证新阈值的性能。将图像Lena和Barbara分别加入gaussian噪声以及salt&pepper噪声。小波变换选用“sym wavelet”，分解层数为2层。

经过200次迭代，适应度（即MSE计算数值）数值基本趋于稳定，Lena和Barbara图像的适应度收敛曲线如图2和图3所示。最佳种群（7维数组）随迭代数的变化如图4所示，HVD小波系数变化过程中阈值的变化如图5所示。

图2 加入gaussian噪声后图像的适应度收敛曲线

图3 加入salt&pepper噪声后图像的适应度收敛曲线

图4 加入gaussian噪声后最佳种群（7维数组）随迭代数的变化

图5 加入salt&pepper噪声后图像HVD小波系数变化过程中阈值变化

由结果图2和图3可知，经过200次迭代后，两幅图像的适应度（MSE）值趋于平稳收敛，且相对于阈值优化前，优化后的适应度函数（MSE）均有较大幅度的下降。根据图4可知，图像去噪迭代过程中，种群中的7个变量均产生了较优的种群并记录更新在新一代种群当中。根据图5可知，HVD小波系数的阈值在迭代过程中变化以实现最小的MSE目标。综上，整个改进遗传算法能较好地实现阈值优化目标。

3.3 图像去噪性能对比分析

Lena和Barbara加入gaussian以及salt&pepper噪声的去噪图像如图6和图7所示。

图6 加入gaussian噪声的图像去噪过程与结果图

图7 加入salt&pepper噪声的图像去噪过程与结果图

由仿真图可知，两幅图在分别加入gaussian噪声与salt&pepper噪声之后，均可以达到较好的去噪效果，并且有较好的边缘细节保留效果。

在对以上典型图片进行算法验证后，利用基于caltech数据集对本文的改进算法进行进一步的仿真验证。caltech数据集是由美国加利福尼亚理工学院收集整理的数据集，主要包括两类：一类是caltech101数据集，包括101个类别，每个类别有40到150张图片，共9 144张图片；另一类是caltech256数据集，有256种类别，共计30 607 张图片，

基于caltech数据集的仿真结果如图8所示。

不同去噪算法对caltech数据集图像加入gaussian及salt&pepper噪声后的平均去噪性能曲线如图9、图10所示。

由图9和图10可知，随着噪声方差和噪声百分比的增大，所有算法的去噪SNR均下降，MSE均增加，而改进遗传算法自适应贝叶斯阈值优化算法比VisuShrink、SureShrink算法在SNR与MSE方面有较大提升。

图9 加入gaussian噪声的去噪性能变化曲线

图10 加入salt&pepper噪声的去噪性能变化曲线

针对优化前的BayesShrink阈值算法，利用caltech数据集图像进行阈值优化前后的图像平均边缘细节保持性能结果分析，结果如图11所示。

针对优化前的BayesShrink阈值算法，利用caltech数据集图像进行阈值优化前后的去噪性能结果分析，结果如表1所示。

对于优化前后的BayesShrink阈值算法，分低噪声情况与高噪声情况进行不同的噪声方差（百分比）情况下的去噪计算。由结果可知，caltech数据集图像加入gaussian噪声平均降噪性能提升百分比为12.8%，caltech数据集图像加入salt&pepper噪声平均降噪性能提升百分比为12.4%，图像去噪质量均有较大幅度提升。由图11可知，对于图像边缘细节的保持性能，优化后的BayesShrink阈值算法比优化前平均提升16.6%左右。

图11 图像边缘细节保持性能对比图

表1 本文阈值去噪算法针对caltech数据集图像的去噪性能结果

4 结 语

本文提出了一种基于改进遗传算法的自适应贝叶斯阈值优化方法，仿真结果表明该算法具有良好的性能。由测试结果可知，该算法能够提高图像信噪比，有效减少均方误差，对比各种算法，SNR、MSE均有较大改进，并能较好地保留图像的边缘细节。对比优化前的贝叶斯阈值算法，本文算法图像去噪性能提升12%左右，因此更加有效、实用。尽管本文提出的改进遗传算法自适应阈值优化方法可以有效地去除图像噪声，但算法的计算量仍然较大，算法运行时间较长，有必要在以后的工作中进一步提高算法的效率。