一种基于GMM-Boost的室内定位方法
杨 淼
(1.武汉科技大学 信息科学与工程学院,湖北 武汉 430080;2.常州工程职业技术学院,江苏 常州 213164)
0 引 言
随着计算机、通信及传感等技术的快速发展,获取空间位置信息的手段更加多样化。研究者们开发了许多基于不同通信技术的室内定位系 统[1-4],其中以全球定位系统(Global Positioning System,GPS)和无线局域网(Wireless Local Area Network,WLAN)两种通信技术为代表,分别应用在面向室外和室内的空间位置定位中。基于WLAN的室内定位技术具有广阔的应用前景,能广泛应用于商场导购、展区导览、公共安全及应急响应等服务性领域[5-6]。
由于室内空间存在人员走动、室内温湿度及电磁脉冲等因素影响,某一空间位置上接收到的AP信号会同时受到干扰,不仅导致同一位置上各接入点(Access Point,AP)的接收信号强度指示(Received Signal Strength Indication,RSSI)变化具有相关性,而且造成不同位置上RSSI信号概率分布发生变化。因此,许多基于WLAN的室内定位算法都是通过区分在不同室内空间位置上接收到的接入点(AP)射频信号强度指示(RSSI)概率密度函数不同来达到室内定位的目的。研究发现[7-9],高斯混合模型可以很好地拟合不同位置的RSSI信号概率分布特点,同时其包含的协方差矩阵可以很好地描述多AP的RSSI变化相关性。与其他室内定位算法相比,高斯混合模型更适合捕捉各AP的RSSI变化相关性并精确拟合同一位置RSSI信号概率分布特性。在室内定位应用中,传统的高斯混合模型可以分为有监督式高斯混合模型和无监督式高斯混合模型两种[10-13]。其中,传统有监督式高斯混合模型数据处理步骤包含位置指纹样本标签人工标定、模型训练和位置估计等3步。位置指纹样本标签人工标定是指按照定位误差对采样点进行区域划分,进而对采样点采集到的位置指纹样本根据不同区域赋予不同的位置标签。一般采用最邻近信号采集点归为一类的原则,对采集到的位置指纹样本进行人工区域归类并标定位置样本标签。进而,有监督式高斯混合模型根据标定的样本标签类别数,估计高斯混合模型参数。传统无监督式高斯混合模型数据处理步骤包含聚类簇初始化、模型训练及位置估计等3步。聚类簇初始化一般预先给定模型分布元个数,进而采用K均值、层次聚类及模糊聚类等无监督聚类方法获得相同分布元个数的模型聚类簇。模型训练是指基于获得的模型聚类簇,对相同聚类簇包含的位置指纹样本赋予相同样本标签,进而估计高斯混合模型参数。一方面,虽然有监督式高斯混合模型具有原理简单和可操作性强的优点,但位置指纹样本标签标定原则具有主观性,即由于受到多路径、非视距及运动障碍等时空间因素干扰,按照将最邻近信号采集点归为一类的原则来划分的某类标签样本集不一定都具有相同的信号分布特性,造成划分的采样点组合不是最佳采样点组合,进而导致高斯混合模型在训练过程中无法学习到准确的概率分布特征,影响模型定位结果。另一方面,虽然无监督高斯混合模型可以根据其他聚类方法获得初始聚类簇,但依然无法保证依靠初始聚类簇划分的样本点组合就是最佳样本点组合,聚类效果不佳的聚类簇往往会降低后期模型训练效果和位置估计准确度。此外,不论是有监督式高斯混合模型还是无监督式高斯混合模型,二者都无法在模型训练之前确定最优的高斯混合模型分布元个数,进而导致无法得到拟合所有位置指纹样本信号分布特性的最佳高斯混合模型。如何对不同空间位置获得的位置指纹样本进行自动划分并获得最佳采样点组合,同时摆脱高斯混合模型训练之前需确定分布元个数的束缚选择最优模型分布元个数,对提高聚类方法在室内定位领域中的应用具有重要意义。
针对上述问题,本文首先确定室内空间采样点个数和需要划分的样本标签数,采用第二类斯特林数对采集的位置指纹样本进行集合划分。需要划分的样本标签数是指将空间采样点划分成的区域数目。将被划分在同一区域中的若干采样点视为同一样本标签,可以用于评价定位算法在不同定位误差下的定位误差累积概率分布。按照样本标签数,可以大致估计多大范围内包含了多少样本采集点,将该范围定义为定位误差。考虑到第二类斯特林数数值会随着样本采集点和标签类别数增多而非线性增长,本文结合将最邻近信号采集点归为一类的原则,开发了一种基于阈值的空间位置度量方法,用于过滤同一样本标签下不同样本采集点位置距离过大的标签组合方式,进而尽可能减小高斯混合模型在模型训练阶段的计算量。其次,针对不同样本标签组合,计算由不同个数模型分布元构成的高斯混合模型定位准确率,根据平均定位准确率大小选择最优采样点组合方式。其次,结合贝叶斯信息量准则(Bayesian Information Criterion,BIC)评估高斯混合模型的总体位置指纹样本信号变化特性拟合程度,确定高斯混合模型最佳模型分布元个数。最后,为了进一步提升高斯混合模型位置估计准确度,结合Adaboost算法对高斯混合模型进行定位准确 度提升。
1 原理和方法
1.1 高斯混合模型描述及参数估计
假设室内空间中有M个信号采样点,其坐标分别定义为Pi(i∈{1,2,…,M})。在RSSI采样过程中,在第i个采样点上收集到的H个AP发送而来的N组数据定义为Sij={s1ij,s2ij,…,sHij}(j∈{1,2,…,N}),高斯混合模型将每个采样点上的RSSI概率分布函数描述为多个单高斯分布元加权和,即:

式(3)~式(5)中,p(k|n)为后验概率,表示每个样本符合第k个高斯分布的概率。
1.2 基于第二类斯特林数的采样点组合划分
为了考量定位算法在不同定位误差下的误差累积概率分布,在算法训练之前需要对M个信号采样点进行人工样本标签划分,例如,将同在2 m范围内的采样点划分为同一区域并给予同一位置标签。由于受到多路径、非视距及运动障碍等时空间因素干扰,按照最邻近信号采样点为一类原则划分的采样点组合具有主观性,解决采样点自动划分问题获得最佳采样点划分方式具有实际应用价值。实际上,将M个信号采样点划分成m个样本标签,可以转化为第二类斯特林数计算问题。第二类斯特林数本质上是一种集合的拆分方法,表示将M个不同元素拆σ分为m个子集合的方案数,记为S(M,m),其计算公式为:

根据每一种过滤后的采样点组合方式,对采集到的所有RSSI样本进行组织并赋予样本标签。通过枚举法设定模型分布元个数并构建高斯混合模型,采用留一验证法对训练样本中每个样本进行标签分类并计算最终的定位准确度。对不同分布元个数构建的高斯混合模型得到定位准确度进行求和平均,按照平均定位准确度大小,确定标签数为m时的最佳样本标签组合方式。
1.3 基于贝叶斯信息量准则的最优参数确定
高斯混合模型需要估计的参数包括分布元个数、分σ布元权值、分布元均值及协方差矩阵。通常情况下,模型分布元个数由经验值设定。分布元个数设置得太小会导致训练出的高斯混合模型无法有效描述RSSI分布特征,分布元个数设置太大又会增加模型计算量。鉴于此,本文采用贝叶斯信息量准则确定高斯混合模型最优分布元个数。贝叶斯信息量准则是赤池信息量准则的一种改进[14],由于其核心是使用后验概率来选择最佳概率分布模型,因此可以直接用于评价高斯混合模型的优劣。其计算公式为:
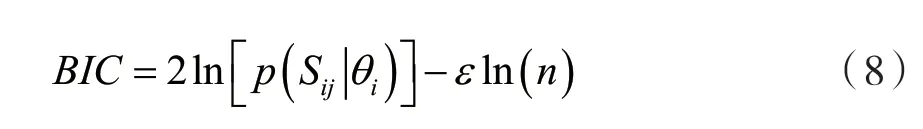
式中:p(Sij|θi)表示高斯混合模型参数为θi时的模型后验概率,ε为惩罚因子,n为RSSI样本 数量。
通过枚举法取值高斯混合模型分布元个数K,采用EM方法估计参数θi,按照不同个数分布元构建的高斯混合模型BIC值大小确定最佳模型分布元个数。实质上,BIC值与熵的物理含义一致,都可以用于衡量体系的混乱程度。因此,在模型训练过程中取最小BIC值对应的分布元个数作为训练高斯混合模型的最优分布元。假设有1个2维矩阵以样本标签数为列,模型分布元个数为行,矩阵每个元素代表样本标签数为m时由k个模型分布元构成的高斯混合模型的贝叶斯信息量,选择贝叶斯信息量最小的矩阵元素所对应的模型分布元个数作为该样本标签数下最佳模型分布元个数。
1.4 基于GMM-Boost的WLAN室内定位方法
基于GMM-Boost的WLAN室内定位方法流程如图1所示,分为在线位置估计阶段和离线模型训练阶段。其中,模型离线训练阶段又分为两个子阶段,阶段一主要完成基于第二类斯特林数的采样点组合划分和基于BIC准则的最佳模型分布元个数确定。阶段二将训练好的高斯混合模型作为弱分类器,通过迭代改变RSSI训练样本权值分布,获得多个高斯混合模型分类器权值,最终组成联级强分类器。值得注意的是,在离线训练阶段一中,存在模型分布元个数与样本标签数m不一致的问题。即当模型分布元个数小于样本标签数时,即使样本标签小于或等于分布元个数的RSSI样本全部分类正确,也始终存在其他标签类全部分类错误的情况。为了保证定位准确率,不考虑模型分布元个数小于样本标签数的情况,当模型分布元个数大于样本标签数时,采用样本标签合并的方法将多出的样本标签归类到其他样本标签上,选择定位准确率最大的样本标签合并方式用于测试样本位置估计。设定模型分布元个数初始值为样本标签数m,然后以1为步长,以2m为上限循环计算每个高斯混合模型的BIC值,进而选择最佳模型分布元个数。
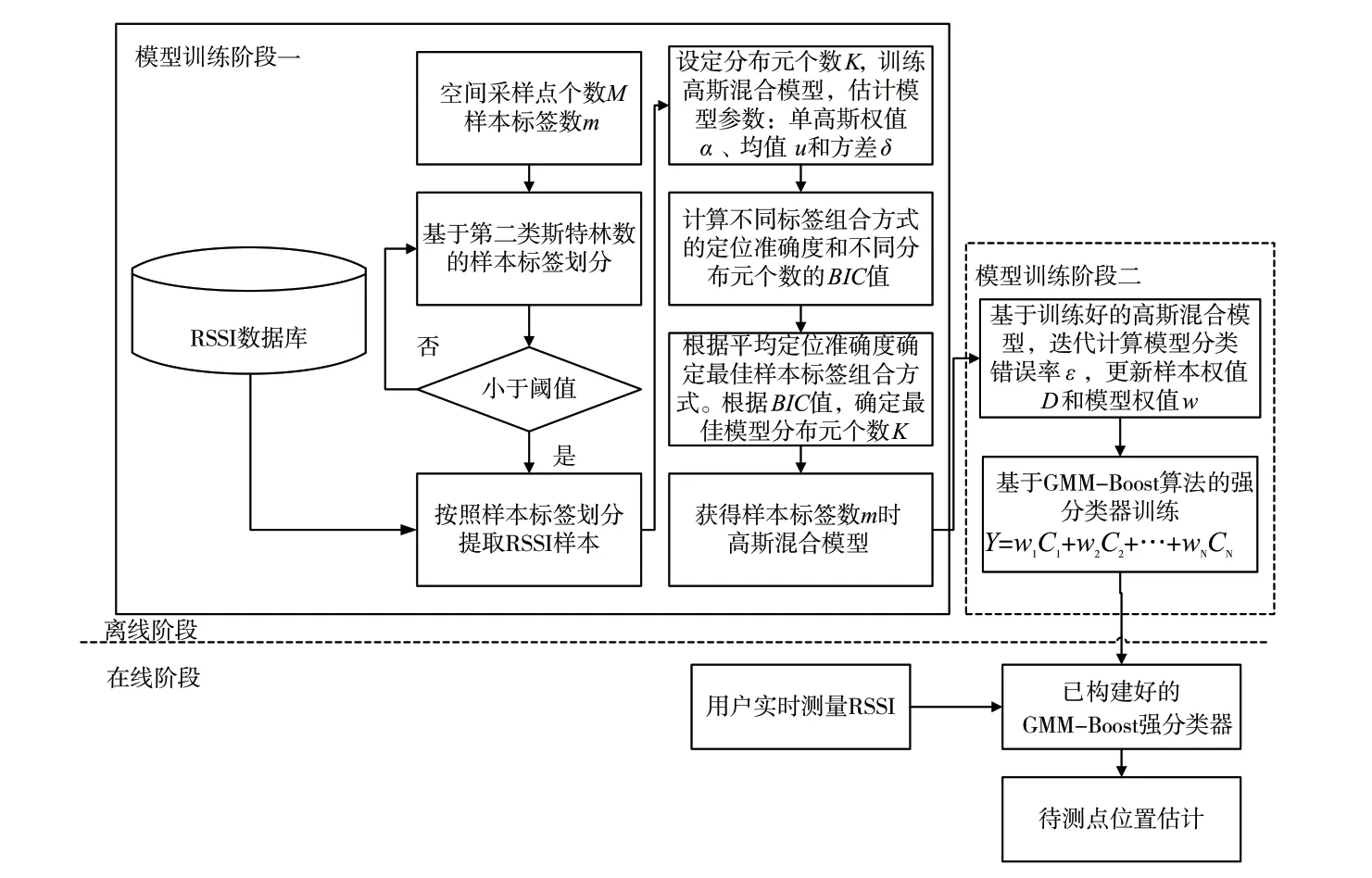
图1 基于GMM-Boost的WLAN室内定位方法流程图
2 实验数据采集
本实验数据采集环境设为南京林业大学主楼2层,实验环境如图2所示。该楼层长约70 m,宽约20 m。由于受到学校区域使用限制,RSSI样本采集点只能在图中A、B、C3个区域进行部署。其中,A区为学生办公区,B区为楼层走廊,C区为电梯等待区。图中三角标志为RSSI样本采集点相对位置,共设有37个采样点。采用笔记本和下载的RSSI信号采集软件,分别在每个采样点上以 1个/秒的采样频率采集RSSI样本,每次采集时间为 1 min左右,每个信号采集点采集两次RSSI样本。每天信号采集时间段为下午2点到5点,连续采集10天。为了研究GMM-Boost算法的泛化能力,课题组将前9天采集的RSSI样本作为离线训练阶段的训练样本,将第10天采集的RSSI样本作为在线阶段的位置估计测试样本。
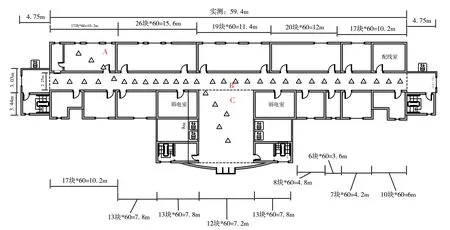
图2 实验环境图
3 实验结果与分析
基于每种不同样本标签数的最佳样本采样点组合,本节分别讨论基于BIC准则的高斯混合模型优化过程和GMM-Boost算法与其他定位算法的定位准确度(测试样本正确分类样本数/测试样本总数)对比。一方面,观察BIC值变化与分布元个数和模型迭代次数之间的关系;另一方面,除了GMM-Boost算法之外,分别实现了有监督GMM(Sup-GMM)、无监督GMM(UnSup-GMM)、支持向量机(LibSVM)、最近邻(KNN)、MLP神经网络(MLP)、随机森林(RF)、朴素贝叶斯(NB)和决策树(DT)等室内定位算法,采用定位准确度衡量不同算法的优劣。实验结果均在MATLAB R2014a环境下实现。按照实际实验环境划分,设定样本标签数为37、18、12、10、8及6,分别对应定位误差0 m、2 m、4 m、6 m、8 m及10 m。例如,在37个采样点,每个采样点间隔2 m的情况下,当样本标签数为37时,一个样本标签只包含一个样本采集点,将其定义为定位误差为0 m。同样,当样本标签数为18时,大部分样本标签包含两个样本采集点,这两个样本采集点被包含在直径为2 m的圆中,将其定义为定位误差在2 m左右。
3.1 基于BIC的高斯混合模型优化过程
图3给出了由不同分布元个数组成的高斯混合模型进入稳态所需的模型迭代步数。从图中可以得出,分别由18~25个分布元构成的高斯混合模型在50步左右对应的贝叶斯信息准则值不再变化,表明模型已经进入了稳态模式,通过更新模型参数θi,其似然函数值已达到最大并且变化不明显。鉴于此,针对由不同个数分布元构成的高斯混合模型,在模型训练阶段一律取50作为模型迭代步数,观察分布元个数与模型BIC值之间的关系。
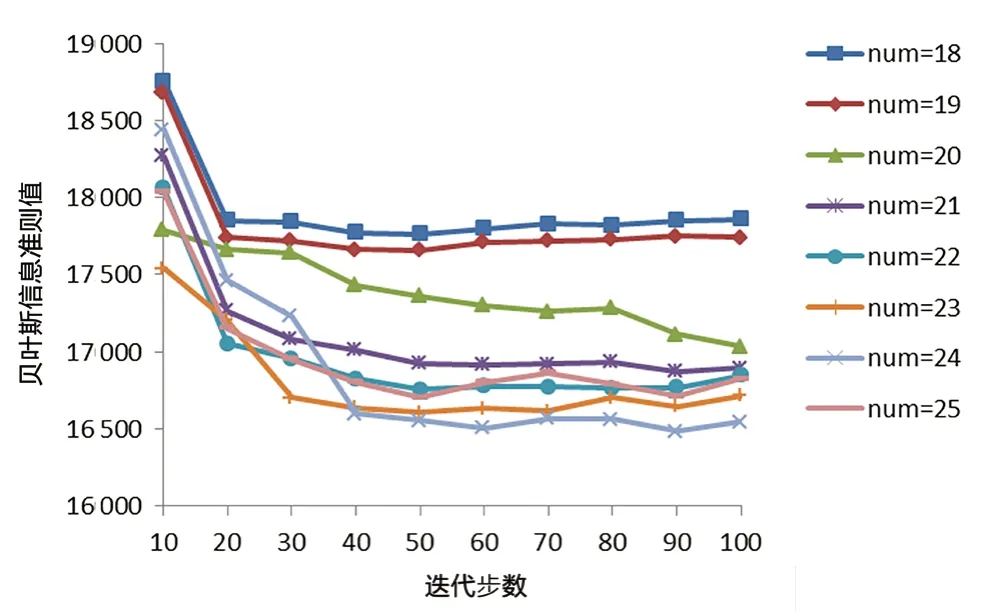
图3 算法学习与BIC优化过程
图4 给出了样本标签为18、对应定位误差为 2 m时,分布元个数与模型BIC值以及定位准确度的关系。BIC值和定位准确度的取值范围不一样,为了方便显示,将BIC值映射到[0,1]范围内。从图中可以看出,当分布元个数为24时,模型的贝叶斯信息准则量最小,说明样本标签个数为18时,最优模型分布元个数为24。图4也给出了相同条件下由不同个数分布元构成的高斯混合模型的定位准确度。从图4可以看出,BIC曲线与准确度曲线负相关,当模型分布元个数为24左右时,模型定位准确度达到最高,说明采用BIC选择模型最佳分布元个数具有合理性。
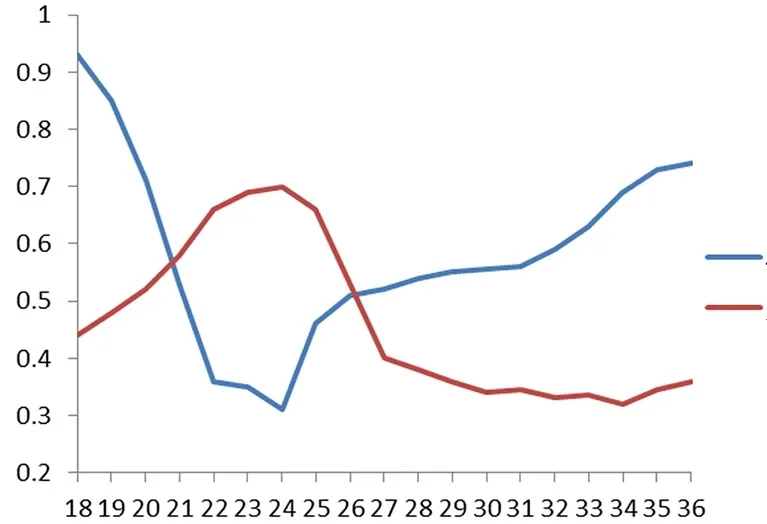
图4 稳态时分布元个数与BIC值关系
3.2 与其他定位算法的定位精确度对比
图5 给出了基于划分的训练样本和测试样本各个算法的定位准确度,即定位误差累积概率分布。定位误差为2 m时,GMM-Boost、Sup-GMM、UnSup-GMM、LibSVM、MLP、RF、NB、DT及KNN的定位准确度为71.2%、52.3%、50.5%、58.3%、46.6%、55.8%、65.7%、42.6%及36.2%。当定位误差为4 m时,各个算法的定位准确度依次 为81.2%、63.5%、60.8%、69.1%、53.4%、68.1%、75.6%、49.5%及42.7%。GMM-Boost算法定位准确度明显高于其他定位算法。Sup-GMM和UnSup-GMM由于没有采用最佳分布元个数确定方法,限制了高斯混合模型拟合位置指纹概率分布特点的能力,两者定位准确度也低于LibSVM、RF和NB等算法。同时,定位误差为0 m时,GMM-Boost定位准确度为55%,而其他算法定位准确度都小于50%,原因在于只要弱分类器分类准确度达到50%,由Adaboost算法训练的联级分类器便可提升样本分类准确度。在模型训练阶段,将已经优化过的GMM模型作为弱分类器,并结合Adaboost算法通过改变样本权值分布获得由不同权重值组成的联级分类器,提升了GMM-Boost算法对测试样本的分类准确度。
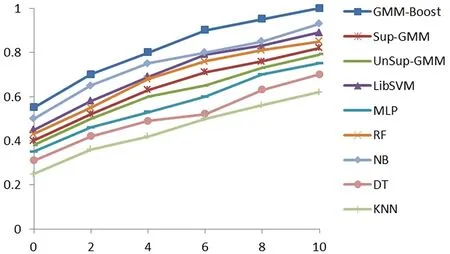
图5 各个算法不同定位误差累积概率分布
图6所示为各个算法的平均定位误差随样本位置采样点样本个数的变化。当样本位置采样点样本个数为500时,GMM-Boost算法平均定位误差为1.75 m,仍然低于其他定位算法在样本个数为1 000时的平均定位误差。当采样点样本个数为100时,GMM-Boost平均定位误差为3.1 m,相对于Sup-GMM和UnSup-GMM算法,二者想要获得同样的定位效果采集点样本个数至少需要400。同时可以看出,随着样本采样的增多,GMM-Boost的平均定位误差下降速度要大于其他算法,主要原因在于结合了Adaboost算法的GMM-Boost具有良好的泛化能力,能较好地避免过拟合问题。因此,在提高定位准确度的同时,GMM-Boost可以大大减小离线阶段的数据采集工作量,进而促进定位系统的大规模部署应用。
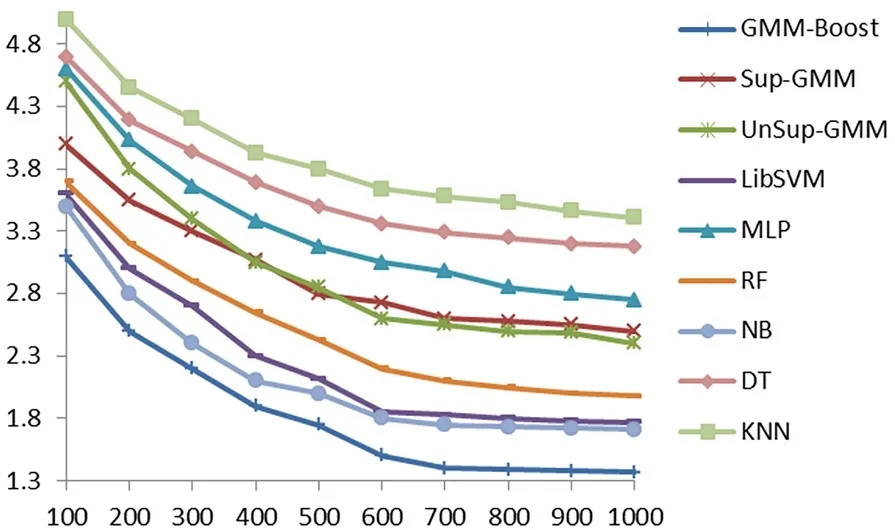
图6 各个算法平均定位误差随采样点样本个数的变化
4 结 语
针对高斯混合模型在模型训练之前采样点无法自动划分以及无法确定最佳分布元个数的问题,提出了一种基于GMM-Boost的WLAN室内定位方法。该算法首先采用第二类斯特林数将不同样本采样点划分为若干组合方式并赋予不同样本标签,分别针对不同样本标签数设定不同模型分布元训练高斯混合模型,根据模型的平均定位准确度选择某一样本标签数下最佳样本采样点组合方式,为离线阶段样本位置点划分方式的优劣提供了评价标准和技术路线,避免了人工划分方式的主观性。其次,结合贝叶斯信息量准则,计算由不同分布元个数组成的高斯混合模型贝叶斯信息量,选择信息量最小所对应的分布元个数作为模型的最佳分布元个数。最后,为了进一步提升模型定位准确度,将已经优化过的GMM模型作为弱分类器,结合Adaboost算法更新训练样本权值分布进而组成由不同权值构成的联级强分类器。实验结果表明,与其他定位算法相比,GMM-Boost算法具有较好的定位准确度和泛化能力,并且只需较少的样本个数便可以获得较低的平均定位误差,降低了离线阶段人工数据采集工作量。然而,由于GMM-Boost模型在模型训练阶段需要考虑的因素较多,因此需要较长时间获得最佳高斯分布模型。在未来工作中会对基于高斯混合模型的室内定位算法进行先验知识总结,促进室内定位系统大规模部署。

