四肢格构式柱金属结构拓扑优化设计

杨 雪，程文明，李银启，张 军

（1.西南交通大学机械工程学院 四川 成都 610031；2.轨道交通运维技术与装备四川省重点实验室，四川 成都 610030）

1 引言

随着我国的基础设施建设的发展，格构式柱金属结构在工程机械中有广泛的应用[1]，使得四肢格构式柱朝着更加轻量化的方向发展。在工程中所用到的四肢格构式柱通常不是由四个钢板以及四个角钢（肢脚）所组合在一起的，而是由缀条（缀材）或者缀板搭配角钢所组成。为了方便，以钢板及角钢所组成的格构式金属结构来进行拓扑优化，由于运用ANSYS软件进行拓扑优化容易形成棋盘格效应，这里采用ABAQUS 软件进行拓扑优化分析，以便得出合理的拓扑结构[2-3]。目前工程上比较常用的几种四肢格构式柱外形，如图1所示。

图1 工程上的几种格构式柱Fig.1 Several Lattice Columns on the Project

第一种为K型格构式柱，第二种为E型格构式柱，第三种为人型格构式柱。为了分析拓扑优化后得到的结构的效果，通过ANSYS有限元软件对拓扑优化后的结构进行建模[4]，同时比较拓扑优化后的金属结构与K型、E型及人字形格构式柱的应力及变形量，分析得出拓扑优化后的结构从质量与应力及变形上较现有的格构式金属结构有所优化，结构稳定性也较好，为工程上的应用提供了参考。

2 拓扑优化模型

对四肢格构式柱金属结构的四个面进行拓扑优化，以最小柔度C作为优化目标，将材料优化的体积缺省比K和优化后的体积V作为约束条件[5]，寻求结构的合理分布。一般情况下，基于变密度法的拓扑优化的数学模型如下：

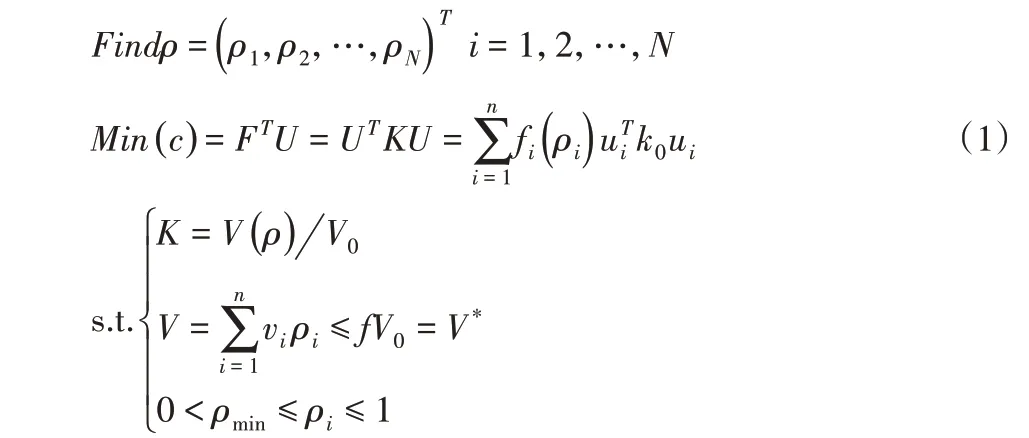
式中：ρi—设计变量，是单元的相对密度；n—设计变量个数；C—目标函数，是结构的应变能；K—结构总体刚度矩阵；F—结构所受载荷；U—结构的总体位移向量；ui—单元i的位移向量；k0—ρi=1 时的单元刚度矩阵；fi(ρi)—惩罚函数；V—结构优化后的体积；vi—单元i的体积；f—给定材料体积比；V0—初始结构体积；V*为体积上限；引入ρmin是为了避免总刚度矩阵奇异，通常取为0.001[6]。

3 ABAQUS结构拓扑优化设计

3.1 有限元模型的建立

四肢格构式柱采用SHELL 板壳单元，弹性模量EX=2.1E5（MPa）；泊松比PRXY=0.3；钢材密度DENS=7.85E-6（kgmm3），材料选择Q345 钢，其许用应力为345MPa[7]。选取长和宽均为310mm，高为1900mm，板厚为3mm的格构式柱，结合ABAQUS软件的part部分对其进行参数化建模模型，如下图2所示。

图2 格构式柱的初始有限元模型Fig.2 Initial Finite Element Model of a Lattice Column

3.2 边界条件与载荷施加

由于格构式柱在工程上一般用来承载，选取格构式柱的两边中心点，在ABAQUS的功能模块interaction中分别给两个点和其所在的平面上的角钢施加耦合约束，在Load模块中给其中一端的中心点施加力，给两侧面（X轴和Y轴）均施加200kN的力，给轴向（Z轴）施加800kN的力。另一端完全约束格构式柱的6个自由度，如图3所示。

图3 施加耦合约束的模型Fig.3 Model Applying Coupling Constraints

3.3 拓扑优化结果

在ABAQUS中的Optimization功能模块中，选择格构式柱的四个面（除去角钢）为优化区域，依次定义设计变量、目标函数和约束条件。设置不同的缺省比K（K从0.3-0.7进行取值），得到不同的优化结果，如图4～图8所示。

图4 缺省比K=0.3时的拓扑优化结果Fig.4 Topology Optimization Results When the Default Ratio K=0.3

图5 缺省比K=0.4时的拓扑优化结果Fig.5 Topology Optimization Results with Default Ratio K=0.4

图6 缺省比K=0.5时的拓扑优化结果Fig.6 Topology Optimization Results with Default Ratio K=0.5

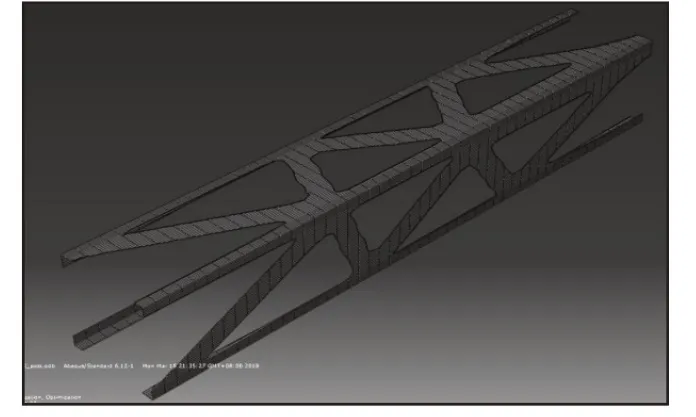
图7 缺省比K=0.6时的拓扑优化结果Fig.7 Topology Optimization Results with Default Ratio K=0.6

图8 缺省比K=0.7时的拓扑优化结果Fig.8 Topology Optimization Results with Default Ratio K=0.7

通过上述不同缺省比的拓扑优化结果可以发现当缺省比K＜0.5时，材料的利用率比较小，当缺省比K＞0.5时，材料的连接已经开始出现问题。所以当K=0.5时，所得的结果较好，比较合理，对K=0.5的拓扑优化结果重新进行设计[8]，运用ANSYS有限元软件进行建模，得到的有限元模型，如图9所示。

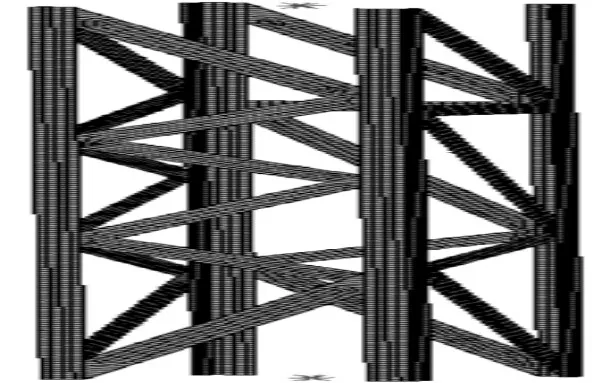
图9 格构式柱拓扑结构有限元模型Fig.9 Grid Element Topology Finite Element Model

4 校核与分析

通过对优化后的格构式柱和图1中其他的格构式进行有限元模型的建立，分别进行计算，对比分析得出，拓扑结构与图1中的几种格构式柱的等效应力云图，如图10所示。竖直方向应力变形，如图11所示。图形的顺序从左到右均是按照拓扑优化后的格构式柱、K型结构、E型结构、人字形结构进行排列。拓扑图形与图1中的格构式柱的应力、变形与质量的结果，如表1所示。

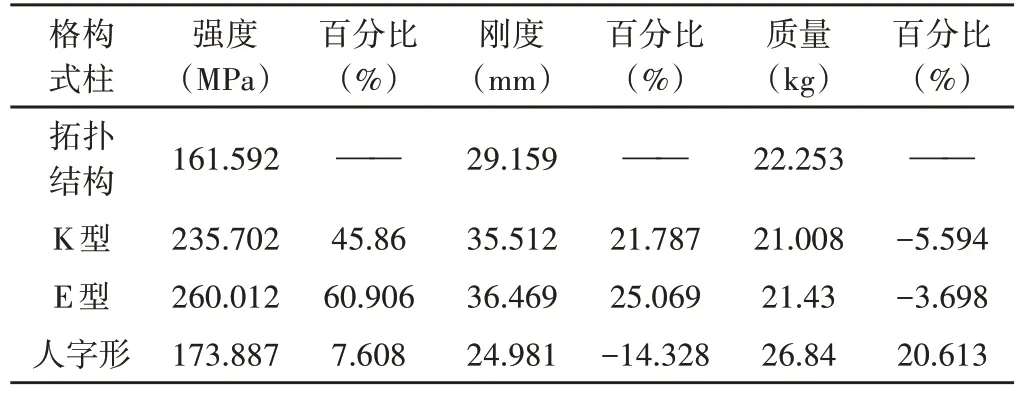
表1 格构式柱的对比结果Table.1 Comparison Results of Lattice Columns

图10 拓扑结构、K型、E型、人字形格构式柱的等效应力云图Fig.10 Equivalent Stress Cloud Diagram of Topological Structure，K-type，E-type，Herringbone Lattice Column

图11 拓扑结构、K型、E型、人字形格构式柱的变形Fig.11 Deformation of Topological Structure，K-type，E-type，and Herringbone Lattice Columns

通过上表对比分析，可以知道拓扑优化后的结构的最大等效应力是161.592MPa，最大变形量为29.159mm，这几种结构的最大应力均小于许用应力345MPa，符合应力强度校核。

从应力变形上进行对比分析，拓扑优化后的结构应力比其他三种结构的应力小，变形比人字形结构的变形大（14%左右），但是比K型、E型结构的变形分别小了21.7%、25%。从质量上进行对比分析，拓扑优化后结构的质量较轻，虽然比K型、E型结构的质量稍重（5%左右），在可接受范围内，但是比人字形结构的质量轻很多（20%左右）。

综上所言，拓扑优化后的结构比较合理，稳定性较好。

5 结论

（1）拓扑优化设计是一种高效可靠的优化方法，不仅适用于格构式柱结构，同时也为工程中其他结构的拓扑优化设计提供了参考。（2）拓扑优化设计的缺省比是拓扑优化的重要参数之一，对拓扑结果有着极大影响，选择合适的缺省比是获取好的拓扑结构的关键。（3）拓扑后的格构式柱结构通过强度和刚度校核，与现有格构式柱对比，在应力变形与质量上都有不同程度的优势，拓扑结构较合理。