Volterra 型算子从导数Hardy 空间到加权Dirichlet空间上的序有界性

罗庆仙

（广东茂名幼儿师范专科学校 理学院，广东 茂名 525200）

用H（Δ）表示复平面单位圆盘Δ上所有解析函数f组成的函数空间.对于g∈H（Δ），Volterra 型算子Tg及其伴侣算子Sg的定义分别如下：（Tgf）（z）=f（ζ）g'（ζ）dζ，（Sgf）（z）=f'（ζ）g（ζ）dζ，其中，z∈Δ，f∈H（Δ）.这两个算子通过乘法算子Mg（f）=gf联系在一起：Mg（f）（z）=g（0）f（0）+Tg（f）（z）+Sg（f）（z）.

Volterra 型算子在各种函数空间上的有界性和紧性等问题的研究一直是一个热门的研究课题. Pommerenke 在研究BMOA 函数的增长性时首次研究并刻画了Volterra 型算子Tg在Hardy-Hilbert 空间H2上的有界性［2］.之后，Aleman 等系统地研究了Volterra 型算子Tg在Hardy 空间Hp（0＜p＜∞）上的有界性和紧性条件［3-4］.关于Volterra 型算子Tg在Bergman 空间上的有界性和紧性的相关工作可参考文献［5］.值得注意的是，肖杰研究了一种新型Qp空间上的Carleson 测度问题并由此刻画了Volterra 型算子Tg的有界性等性质［6］.关于这类算子在其它一些解析函数空间的研究可见参考文献［7-8］.

序有界性在研究一些具体的线性算子的性质时起着重要的角色. Hunziker 等证明了当1≤p≤q＜∞时，若复合算子从Hp到Lq（m）是序有界的，则该复合算子从Hp到Lq（m）是紧的［12］.关于一些相关算子在Hardy 空间和Bergman 空间上的序有界的研究可参考文献［13］.

利用导数Hardy 空间Sp（0＜p＜∞）上的点值泛函δz的范数估计以及导数点值泛函δ'z的范数估计，Lin 等首次研究并指出了Volterra 型算子Tg、Sg及其相关的乘法算子Mg从导数Hardy 空间Sp（0＜p＜∞）到加权Dirichlet 空间（0＜q＜∞，-1＜β＜∞）上的序有界性的完整刻画［13］.

1 Volterra 型算子Tg 及Sg 的序有界性

（2）证明与（1）的证明类似，故略之.证毕.

再由引理1 的（3），类似于定理1 的证明，可得定理2.

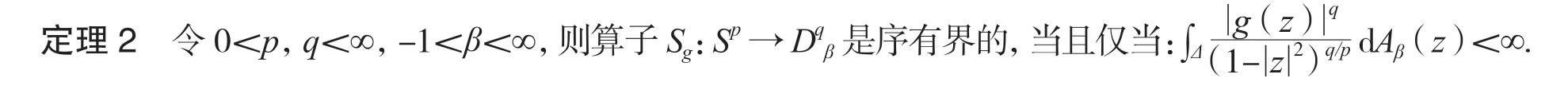
2 乘法算子Mg 的序有界性

这一节主要研究乘法算子Mg从导数Hardy 空间Sp（0＜p＜∞）到加权Dirichlet 空间（0＜q＜∞，-1＜β＜∞）上的序有界性.

（2）证明与（1）的证明类似，故略之.证毕.