基于扩展Dijkstra的多约束QoS路由研究
袁玉莹,付 雄
(南京邮电大学 计算机学院,江苏 南京 210003)
0 引 言
随着Internet网络的广泛应用,一方面由于实时业务对网络传输的时延、丢包率、抖动等特性较为敏感,如果网络中发生突发性的问题,实时业务将会受到很大的影响。另一方面,以太网业务占用了很多的带宽,这对当前的网络传输也提出了挑战。服务质量(QoS)的应用范围涉及到通信网络技术、交通规划、系统工程等很多领域,如何在网络上提供各种业务的QoS保证变得越来越重要。
服务质量(quality of service,QoS)是指由源节点向目的节点传输相应的业务流时,需要满足传输层的某些性能度量约束[1-2]。常见的QoS度量参数包括时延、带宽、代价、丢包率、抖动等,业务在网络传输过程中必须满足QoS约束。QoS约束可以反映在路径约束、链路约束等方面,其中路径约束是指从源节点到目的节点的某条可行路径上,端到端的QoS约束,例如可乘性度量参数时延约束。链路约束指从源节点到目的节点的某条可行路径上每一条链路的约束,例如凹性度量参数带宽约束。QoS度量参数按照性质可以分为可加性度量参数、可乘性度量参数和凹性度量参数[3]。链路的时延、花费和抖动属于可加性度量参数,特点是QoS度量约束总值等于可行路径上所有链路QoS度量之和。链路的利用率和丢包率属于可乘性度量参数,特点是QoS度量约束总值等于可行路径上所有链路的QoS度量之积。带宽属于凹性度量参数,特点是QoS度量约束总值等于可行路径上所有链路的最小QoS度量值。
多约束QoS路由是根据网络中的状态信息以及不同业务对QoS度量参数的要求,为其选择满足多种约束(例如时延、带宽、代价、丢包率和抖动[4-6])的可行路径的一种路由机制。QoS约束可以是一维的参数,也可以是多维的参数,如果业务需要满足多个QoS度量约束时,称为多约束QoS路由。
目前大多数多约束QoS路由研究仅在网络中寻找单一的可行路径或者是单一的最优路径,如果路径上发生局部堵塞或者故障时,分组数据则会丢失,因此以太网业务中的双路径路由主要是在源节点和目的节点之间寻找两条满足多约束QoS条件的最优可行路径,当工作路径堵塞严重或者发生故障时,可以进行主备切换,用另一条保护路径正常进行数据的传输,在一定程度上能够消除路径上的路由振荡问题,同时减轻了网络的负载[7]。
多约束QoS路由计算需要解决的问题是在源节点与目的节点之间找到能够满足多个独立QoS度量参数约束的最优路径。目前国际上主要的研究方法大致分为三种:精确算法(如Dijkstra算法,Bellman-Ford算法)、近似算法(如拉格朗日松弛算法)以及启发式算法(如蚁群算法、遗传算法)[8]。
对于计算多约束QoS路由的可行路径,当可加性约束条件或者可乘性约束条件数量在两个或两个以上的时候,该问题则是一个NP完全问题[9],而研究表明传统的路由算法很难有效地解决NP完全[10-11]问题。在目前所有求解从源节点至目的节点的最短路径的算法中,最为高效的是Dijkstra算法,它可以根据给定的任意条件,快速求解出源节点与目的节点之间的最短路径。该算法的思路是通过预处理去除不满足带宽约束的所有链路边,这样就不需要再考虑带宽的约束。除了带宽约束外,还有其他QoS度量参数约束时,如果约束参数较少,可以使用K-Shortest Path[12]算法,将除带宽以外其他度量参数的约束条件通过某种专门设计好的函数转化为一个单独的度量参数约束[13]。这种方法的优点是能够去除所有不能同时满足多个QoS约束条件的路径,但是当QoS度量参数约束较多时,该方法几乎不能找到一个合适的函数将多个QoS度量参数转化为一个度量参数。
因此针对所研究的多约束QoS双路径路由问题,文中设计了一种基于扩展Dijkstra的多约束QoS双路径路由算法(multi-constrained QoS dual-path routing algorithm based extended Dijkstra,ED_MCQDP),旨在网络中寻找到能够满足多个QoS度量参数约束并且求解精度较高的双路径路由。
1 蚁群算法基本原理
蚁群算法,又称蚂蚁算法,由意大利学者Dorigo等人提出,是一种寻找图中最优路径的概率型算法[14],最初应用于解决旅行商问题,目前扩展到用于解决交通路由、资源分配、通信网络中的路由问题以及负载均衡等[15]。
算法1:蚁群算法。
输入:节点集合M,蚂蚁数量n,迭代次数c
输出:最优路径path
1.τij(0)=0// 设置初始信息素
2. for(i=0;i 3. for(j=1;j<=n;j++) 4. if(q>q0) 7.τij(t+1)=(1-ρ)τij(t)+ρΔτij// 经过的路径信息素全局更新 8.τij(t+1)=(1-ρ)τij(t)// 其他链路信息素更新 9. end if 10. end for 11. end for 12. return path 蚁群算法的选择概率公式如下: (1) (2) 蚂蚁每走一步或者完成一次遍历之后,需要更新残留的信息素,对旧的信息素进行一定程度的挥发,避免累积过多的残留信息素,导致启发信息被淹没。蚂蚁k从节点i移动到节点j之后,利用公式(3)迭代更新节点i和节点j上的信息素浓度,其中ρ为信息素挥发因子(ρ的取值范围是[0,1]),则1-ρ是信息素残留因子。 (3) (4) 其中,Q是常数,对算法的收敛速度有一定的影响。公式(4)表示信息素增量可以根据QoS度量参数进行动态调整,从而找到时延小、代价小、丢包率小以及抖动小的路径。 蚁群算法使用概率公式进行路径寻找,发现较优解的能力很强,但是该算法在网络规模较大时,搜索时间很长,而且容易陷入局部最优解,并非全局最优解。 Dijkstra算法的基本思想是根据路径权值的大小进行迭代,从而计算出从源节点至目的节点的最优路径[16]。 算法2:Dijkstra算法。 输入:节点个数n,源节点s,目的节点v 输出:最短路径 1.S={2,3,…,n},dist[1]=0,dist[i]=weight(1,i) 2.while (S.length>0) 3.S=S-{j} 4. if (dist[v]+weight(v,t) 5. dist[t]=dist[v]+weight(u,v) 6.end while 7.return path 由算法2可知,Dijkstra算法的核心步骤是从未遍历过的节点中选择路径权值最小的边,该步骤需要遍历所有的节点得到最小权值的边,在网络规模庞大的情况下,搜索时间很长。此外Dijkstra算法是根据单个参数(路径长度的权值)寻找路径,不能直接用于多个QoS度量参数约束的路由计算。 假设G(V,E)表示网络拓扑模型,其中V表示网络模型中所有网络节点(例如交换机、路由器和主机等)组成的集合,E表示网络节点之间的边(即链路)组成的集合,每一条边表示两个网络节点之间的直达通信路径,每个网络节点以及每条边的QoS度量参数均是已知的。假设源节点为s(s∈V),目的节点为d(d∈V)。实际常用的QoS度量参数包括时延(delay)、带宽(bandwidth)、丢包率(loss)、代价(cost)、抖动(jitter),对于网络模型中的任意一个网络节点n(n∈V),给定四种QoS度量参数,分别为时延函数delay(n),丢包率函数loss(n),代价函数cost(n),抖动函数jitter(n)。对于网络模型中的任意一条边e(e∈E),给定四种QoS度量参数,分别为时延函数delay(e),带宽函数bandwidth(e),代价函数cost(e),抖动函数jitter(e)。 定义1(时延):对于任意从源节点s至目的节点d的路由路径P(s,d)(s、d∈V),时延delay(P(s,d))的计算公式如下: (5) 定义2(带宽):对于任意从源节点s至目的节点d的路由路径P(s,d)(s、d∈V),带宽bandwidth(P(s,d))的计算公式如下: bandwidth(P(s,d))=min{bandwidth(e), e∈P(s,d)} (6) 定义3(丢包率):对于任意从源节点s至目的节点d的路由路径P(s,d)(s、d∈V),丢包率loss(P(s,d))的计算公式如下: (7) 定义4(代价):对于任意从源节点s至目的节点d的路由路径P(s,d)(s、d∈V),代价cost(P(s,d))的计算公式如下: (8) 定义5(抖动):对于任意从源节点s至目的节点d的路由路径P(s,d)(s、d∈V),抖动jitter(P(s,d))的计算公式如下: (9) 文中所研究的多约束QoS双路径路由问题即在网络拓扑图G中寻找从源节点s到目的节点d的两条路径,它们均满足公式(10)的约束条件。 (10) 其中,D、B、L、J分别代表以太网业务中QoS度量参数延迟、带宽、丢包率和抖动的约束限制。 在对网络拓扑进行路由查找之前,先对网络拓扑结构进行精简处理,将网络拓扑结构过滤成一个新的简单网络拓扑结构,去除不满足带宽约束的边以及孤立的网络节点,则算法后续不再考虑带宽度量参数的约束,只需要考虑延迟、代价、丢包率和抖动度量参数的约束。 (11) 算法3:ED_MCQOP算法。 输入:网络拓扑图G(V,E);n个网络节点;源节点s;目的节点d;各个网络节点(d,c,l,j)取值;每条链路边的(d,b,c,j)取值;约束条件(D,B,L,J)的值。 输出:两条符合多约束QoS要求的路径p1、p2。 1. remove all links which meet bandwidth(link) 2. remove all isolated nodes which belong toV 3.P={s} 4.N={neighbors ofs} 5. for each nodev∈N 7.f(v)=s// 前一跳节点 8. end for 9. whileN≠Ø 10. minL=min{L(s,v),v∈N} 11. new root=i(i∈the path with minL andi∉P) 12. deleteifromN 13. additoP 14. for each nodej(j∈i’s neighbors andj∉Pandj∉N) 15. addjtoN 16. end for 17. for each nodekini’s neighbors 18. ifk∉PN andL(k)>∑L(s,k) 19.L(k)=∑L(s,k) 20.f(i)=k 21. end if 22. end for 23. end while 24. ifL(s)>(AD+BL+CJ)/cost(P(s,d) return failure 25. else get the first pathp1 26. end if 27. for each nodev∈p1 28. if(v!=s&&v!=d) remove nodevand all links associated with nodev 29. end if 30. end for 31. updatePandN 32. recalculateL(v) 33. ifL(s) > (AD+BL+CJ)/cost(P(s,d) return failure 34. else get the second pathp2 and return pathp1 andp2 35. end if 假设Φ(x)是QoS度量参数中延迟的惩罚函数,如果路径满足延迟度量参数的约束时(delay(P(s,d))≤D),值为1,否则等于rd(0 假设网络拓扑中有m只蚂蚁,n个网络节点,已知每个网络节点的QoS度量参数d、c、l、j取值,以及每条边的QoS度量参数d、b、c、j取值,给定约束限制条件时延D、带宽B、代价C、丢包率L、抖动J的取值,ED_MCQOP算法的伪代码如算法3所示。 基于扩展Dijkstra的多约束QoS双路径路由算法首先对网络拓扑图进行一系列简化,删除不满足带宽约束的所有链路(第1行),以及所有孤立的网络节点,即没有链路链接的网络设备(第2行),在网络规模较大时,该操作可以有效地减少网络规模的复杂度,减少算法的迭代次数。然后构造两个网络节点集合,一个是网络节点集合P,集合P仅包含源节点s(第3行),另一个是节点集合N,包含源节点s的所有邻居节点(第4行),第5行至第8行根据公式(11)引入多约束QoS约束限制,计算由源节点至源节点的所有邻节点的多约束QoS度量值,并存储每个节点的前一跳节点。 记录可行路径中多约束QoS度量值最小的路径,将不属于节点集P的网络节点i标记为新的根节点root,并且从网络节点集N中删除网络节点i,将网络节点i添加到网络节点集P中(第10至第13行),将新的根节点root的所有邻节点(不包括已经在网络节点集P和网络节点集N中的网络节点)添加到网络节点集N中(第14行至第16行)。遍历节点i的所有邻节点,进行多约束QoS度量值的比较更新,核心思想与第2节的Dijkstra算法一致,将满足条件的节点标记值进行更新,更新节点的前一跳节点(第17行至第22行)。 当节点集N不为空时,进行第9行至第23行的迭代,得出具有最优多约束QoS度量值的路径,将其与给定的多约束QoS度量参数值进行比较,如果不满足给定的约束条件,则说明网络拓扑G(V,E)中不存在满足多约束QoS约束限制条件的可行路径,计算路由失败,算法结束(第24行)。否则,得到第一条满足多约束QoS条件的路径p1(第25行)。删除第一条可行路径中除了源节点与目标节点的网络节点以及每条与节点相关的链路(第27行至第30行),该步骤是为了进一步减少网络拓扑的复杂度,减少算法的迭代次数。然后删除网络拓扑中孤立的边和网络节点,更新网络节点集P和网络节点集N(第31行),根据第3行至第23行,重新计算网络节点的多约束QoS度量值L(v)(第32行),将得到的最优多约束QoS度量值的路径与给定的多约束QoS度量参数值进行比较,如果不满足给定的约束条件,则说明当前网络拓扑中,不存在两条满足多约束QoS条件的可行路径,至此,查找路由失败,路由结束(第33行)。否则,得到第二条满足多约束QoS条件的路径p2,至此,获取到两条多约束QoS双路径路由,路由路径计算成功(34行)。 文中所设计的基于扩展Dijkstra的多约束QoS双路径路由算法,考虑到以太网业务在实际网络中,第一条路由路径上的节点所在的不同子网络的规模可能非常大,这样在某些子网络发生故障时,进行主备切换,使用第二条路径进行正常工作,从而大大提高了数据传输的可靠性。同时,本算法在寻找可行性路径的过程中,通过网络拓扑图的精简,减少了网络规模的复杂度,达到了减少算法计算复杂度的目的,并且充分考虑到了多约束QoS约束限制条件,使多约束QoS双路径路由计算能获得最优解且整体可靠性较高。 本实验主要从算法的迭代次数、平均时延、平均带宽、平均代价、平均丢失率以及平均抖动来分析算法的性能。算法的迭代次数是指该算法从开始运行到最终返回满足多约束QoS的两条路径或者查找路由失败结束所需的迭代次数,与算法的时间复杂度有关。在该实验中,为了减少实验误差,选取了100对源节点和目的节点,通过重复进行实验计算平均值的方法获取算法的平均迭代次数。 实验所采用的不同规模的网络模型均由基于MPLS的网络管理系统通过批量建立离线设备节点生成,网络节点数量分别设置为100、200、300、400和500,选取时延、代价、抖动三个可加性度量参数、一个可乘性度量参数丢包率以及一个凹性度量参数带宽,由随机数生成器生成一定区间内的随机数,在不同的网络规模下分别运用基于扩展Dijkstra的多约束QoS双路径路由算法、蚁群算法、遗传算法记录算法的迭代次数、时延、带宽、代价、丢包率以及抖动。 图1表示网络拓扑图中在不同的网络规模下,ED_MCQOP算法、蚁群算法以及遗传算法的平均迭代次数。从图中可以看出,随着网络规模的增加,算法的平均迭代次数也随之增加。同时,蚁群算法的平均迭代次数增长得最快,ED_MCQOP算法的平均迭代次数在不同网络规模下相对于蚁群算法和遗传算法都较少。 图1 不同网络规模下三种算法的平均迭代次数 假设时延约束delay=30 ms,图2表示网络拓扑图中不同网络规模下ED_MCQOP算法、蚁群算法以及遗传算法的平均时延。从图中可以看出,相较于蚁群算法和遗传算法,ED_MCQOP算法的平均时延大多数情况下相对较低。 图2 不同网络规模下三种算法的平均时延 假设带宽约束bandwidth=15 Mbit/s,图3表示网络拓扑图中不同网络规模下ED_MCQOP算法、蚁群算法以及遗传算法的平均带宽。从图中可以看出,相较于蚁群算法和遗传算法,ED_MCQOP算法的平均带宽大多数情况下相对较低。 图3 不同网络规模下三种算法的平均带宽 假设代价约束cost=30,图4表示网络拓扑图中不同网络规模下ED_MCQOP算法、蚁群算法以及遗传算法的平均代价。从图中可以看出,一般情况下,ED_MCQOP算法的平均带宽相对较低。 图4 不同网络规模下三种算法的平均代价 假设丢包率约束loss=4.5×10-3%,图5表示网络拓扑图中不同网络规模下ED_MCQOP算法、蚁群算法以及遗传算法的平均丢包率。从图中可以看出,相较于蚁群算法和遗传算法,ED_MCQOP算法的平均丢包率大多数情况下相对较低。 假设抖动约束jitter=20 ms,图6表示网络拓扑图中不同网络规模下ED_MCQOP算法、蚁群算法以及遗传算法的平均抖动。从图中可以看出,相较于蚁群算法和遗传算法,ED_MCQOP算法的平均抖动大多数情况下相对较低。 图5 不同网络规模下三种算法的平均丢包率 图6 不同网络规模下三种算法的平均抖动 文中基于扩展的Dijkstra算法和蚁群算法的融合,研究包含延迟、带宽、代价、丢包率和抖动度量参数的多约束QoS双路径路由问题,实验结果表明,基于扩展Dijkstra的多约束QoS双路径路由算法在求解性能上优于蚁群算法和遗传算法,可用于求解网络拓扑中的NP完全问题。




2 Dijkstra算法基本原理
3 基于扩展Dijkstra的多约束QoS双路径路由算法设计

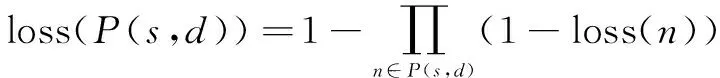




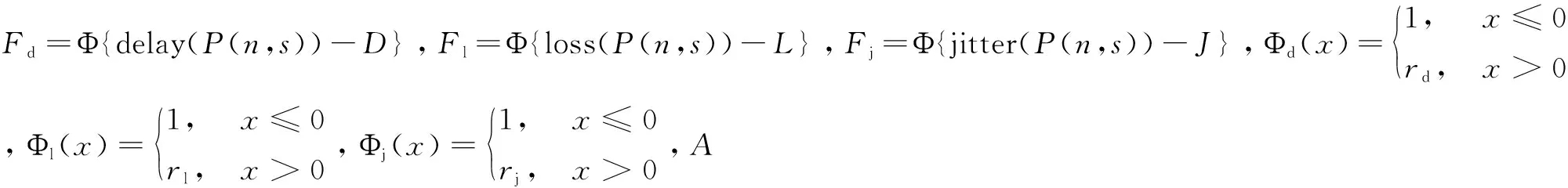
4 实验结果与分析






5 结束语

