关于图形旋转变换专题的解题方法探究

摘要：图形的旋转变换过程大多伴随着其它因素的改变，在旋转变换之后整个数学题目的难度也会由此增大.本文基于初中数学图形旋转变换题解题展开探讨，论述了其在判断图形形状、证明线段数量关系、确定图形位置关系中的应用.帮助学生由旧知识串联起新的知识，通过位置变换后的重新组合做出全等代换.让学生理解清楚各种图形的变换关系，找到正确的解题路径.

关键词：初中数学;图形旋转变换;解题方法

中图分类号：G632文献标识码：A文章编号：1008-0333（2021）29-0048-02

《数学课程标准》提出了数学教学总体目标，其中包括了学生对于数学图形旋转变换的认知，并要求学生掌握几何图形的基础知识.对于初中数学课堂上的图形旋转变换题，教师应帮助学生探索线段、平行四边形、多边形等基本图形的相互特征.通过变换演示了解图形的前后对应关系.知晓图形变换题的一般化解决步骤，让学生不再畏惧图形的旋转变换题目.

一、判断图形的具体形状

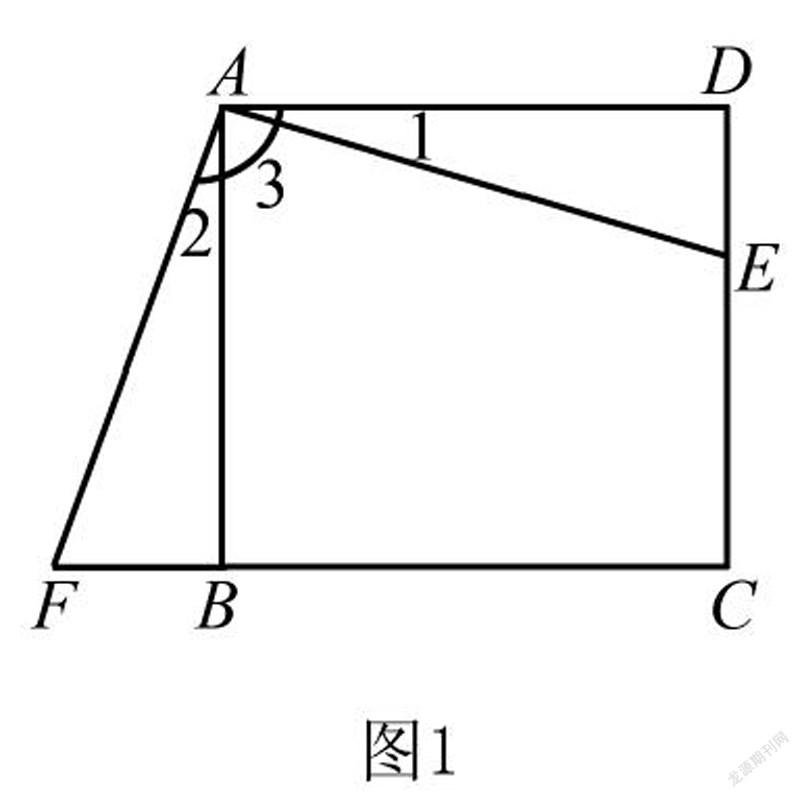
例1已知图1的四边形ABCD是正方形，三角形ADE通过顺时针旋转与三角形ABF重合.

（1）旋转中心位于哪里？

（2）图形总共旋转了多少度？

（3）如果连接了EF，那么三角形AEF是什么三角形呢？

对于该道题目的解答，教师应着重帮助学生领会到旋转变换的具体概念以及其变换后的基本性质.学生能够通过观察直接写出第一问和第二问的答案，但是对于第三问，一些学生在进行解题时却遇到了一些麻烦.此时教师就应该组织学生进行合作探讨，帮助学生回顾之前所学习过的知识.了解三角形的形状有直角三角形、等腰三角形、等边三角形，之后再由旋转和它所旋转的图形得知对应点到旋转中心的距离相等.而两组对应点还分别与旋转中心连线所对应的两个角相等，由此学生也会很容易的去连接线段EF.并利用好AE=AF，得出∠FAC +∠1=∠2=90°，由此去判断出三角形AEF就是等腰直角三角形.在解答这一类的数学问题时，教师应由图形的旋转变换关系进行入手.鼓励学生在分析过程中了解旋转变换过后的变与不变关系，让学生分清图形的基本形状，了解旋转的必要特征.在此基础之上，教师还要对基本题目进行适当拓展.帮助学生理解不同变换模式下的图形形状，真正打好学生对于图形旋转变换题的认知基础.

二、证明线段之间的相关数量关系

例2如图2，已知三角形ABC中AC=BC，∠C=90°，D是AB上任一点，DB+AD=2CD.

对于这道題目的解答，教师要引导学生抓住旋转变换题目的解题关键就是旋转后图形与旋转前图形属于全等关系.由此利用好旋转角度的变化特点，通过化归思想解决问题.其具体解题步骤是这样的――先将三角形ACD绕C点逆时针旋转90度后再连接线段ED，得出三角形BDE是直角三角形，而三角形CDE则是等腰直角三角形.将分散的线段划归到两个直角三角形中，最后由勾股定理得到ED=CD+CE=2CD.

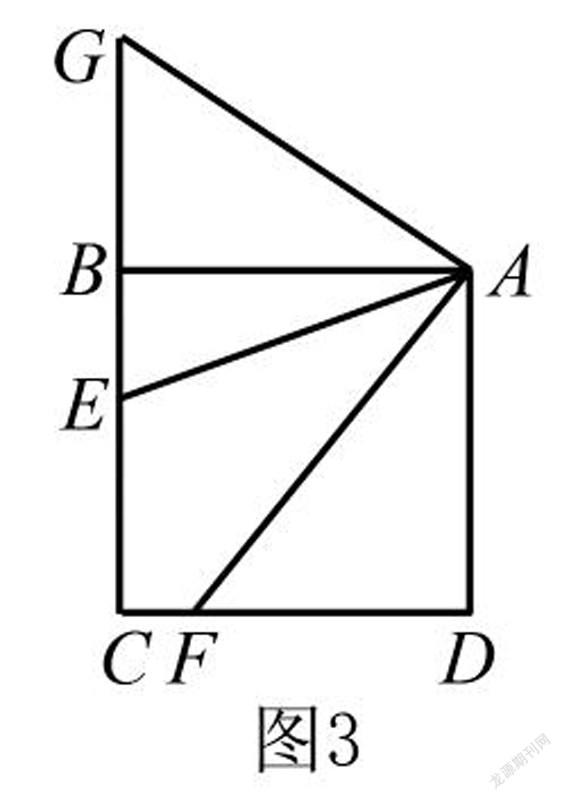
例3如图3，已知正方形ABCD，E为BC上任一点，且AE=BE+FD交CD于F点，证明AF平分∠DAE.

这道题目的解题要点仍和上道题目一样，也是将三角形ADF围绕A点进行旋转的.由此可以得知三角形中AE=EC=BE+FD.再利用好正方形的相关性质得出∠DAF与∠FAE相等，最终通过旋转变化解答.教师在教学时应帮助学生寻找到旋转过程中变与不变的量，攻克线段数量关系变换，从而达到解题目的.

图形旋转变换题是新课改以后，图形与几何部分知识的重要考察内容，教师在淡化证明过程时也应该加强学生对于图形旋转变换题的了解.培养学生的空间素养，让学生知晓不同图形旋转变换题的解题关键.融入合适的数学知识点，帮助学生建立数学知识的学习脉络.重视学生的已有经验，让学生在自主探究过程中了解图形旋转变换题的真正解题技巧.

参考文献：

[1]盛元.初中数学解题方法之旋转[J].数学学习与研究（教研版），2014（2）：110-111.

[2]汤永东.变换思想在初中数学教学中的应用[J].中学数学（初中版），2008（12）：30-31.[责任编辑：李璟]

作者简介：吴艳华（1983.12-），女，江苏省苏州人，本科，中学高级教师，从事初中数学教学研究.