哥德尔定理中递归结构在图形设计中的探究

摘要:本文简要分析自我递归结构在埃舍尔几幅著名作品中的应用,以图形设计过程中设计灵感的获取、设计程序的敲定、设计信息的提炼之间的内在联系为基础,对获取的设计元素在图形视觉形态上进行整合,最终应用于图形设计的设计实践中,为今后的递归结构应用到图形设计领域以及数理逻辑与艺术设计领域的结合提供科学理论研究与案例参考。
关键词:哥德尔不完备定理 递归函数 埃舍尔 图形设计
美国作家侯世达的《哥德尔,艾舍爾,巴赫——集异璧之大成》一书,将哥德尔的数理逻辑、埃舍尔的版画、巴赫的音乐贯穿在一起,揭示出三者之间“三位一体”“殊途同归”的关系。哥德尔深奥的数理逻辑与埃舍尔的版画和巴赫的音乐有着相同的“自指递归”。埃舍尔用他的版画表现出视觉艺术的怪圈,他的名言是“谁敢确定地板不是天花板”;本着自指递归的思维,巴赫创造出“合理错位”但结尾又能回到开头的《卡农》;哥德尔依靠数理逻辑来推理数理逻辑本身,从而创造出了哥德尔不完备定理。
一、哥德尔定理简述
(一)哥德尔不完备定理
作为数学界最重要的定理之一,其“不完备定理”的影响已经远远超过了数学领域,尤其是哥德尔的不完备定理在推理过程中使用的原始递归函数如今在元数学、逻辑学、音乐、艺术设计方面也产生重要影响。
哥德尔不完备定理认为:在一个足够复杂的公理体系形式系统中(包含皮亚诺算术公理),都存在一个命题,它在这个系统内既不能被证明也不能被否定。简言之,哥德尔认为:数学系统是不完备的,并且还是不可完备的。
(二)递归函数与递归结构
据甘迪(Robin Gandy,1919—1995)考证,首先使用“递归”术语的人是形式主义学派“首领”希尔伯特。原始递归函数是由哥德尔首先提出来的,现如今仍然是计算机理论的一个重要概念。所谓的原始递归函数是指由初始函数开始,经过有限次数的代入于原始递归式而作出的函数。
不管是哥德尔首先提出的原始递归函数,还是后来提出的一般递归函数,其实都是一种典型的递归结构。递归函数关系本质是一种迭代关系,而迭代实质上是一个循环反馈的过程,即由最初的函数(或自身)作为“输入”,由“输入”通过递归得到“输出”,随后把得到的“输出”再作为“输入”引入函数,不论是多复杂的递归函数,都可以看作是一种把“果”又当成“因”的循环迭代过程。这样一种互为因果、互为输入与输出的循环迭代过程就是递归过程或成为递归结构。而这种互为因果、互为输入与输出的循环过程在埃舍尔的版画中体现得淋漓尽致,创造出了许多令人惊奇的图形设计作品。
哥德尔当时所说的一般递归函数,可根据它本身的定义理解为“在有限证明步骤内可以计算的函数”。如今数学界已经证明:可以从初始函数开始以有限步骤计算出的函数都是递归函数。在《哥德尔,艾舍尔,巴赫——集异璧之大成中》,作者通过自指递归思维将哥德尔不完备定理,埃舍尔自相缠绕的版画,巴赫循环上升最终又回到起点的音乐三者紧密联系在一起。本文重点探讨递归结构在埃舍尔版画中的应用以及与图形创新设计的结合。
二、递归结构在埃舍尔版画中的应用
作为20世纪荷兰著名版画家的埃舍尔,他的画作因包含大量的数学性、物理性以及哲学性被许多数学家、画家所喜爱。埃舍尔将二维空间里视觉元素以及递归过程描绘在三维空间的真实场景中,并且画面没有一丝违和感,其中自相缠绕的怪圈或自指递归过程经常作为主体出现在他的画中。
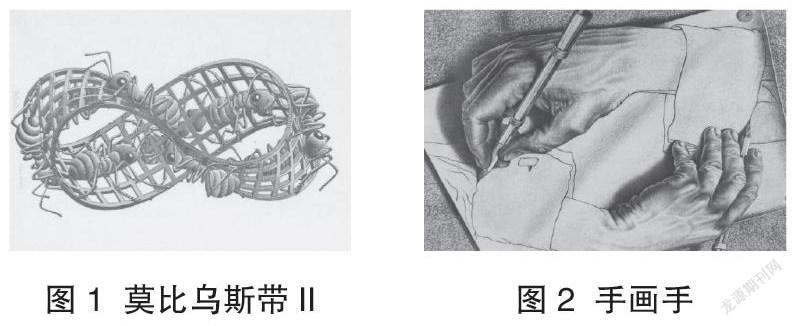
1960年,英国数学家莫比乌斯劝埃舍尔创作一幅表现莫比乌斯带的版画,随后埃舍尔在充分了解莫比乌斯带后创作出一系列优秀的拓扑学版画,例如《莫比乌斯带II》(图1)。《莫比乌斯带II》中的这只蚂蚁沿着莫比乌斯带走了一整圈最后又回到原位,没有跳跃,也没有跨越什么边界,无可辩驳地证明这个结构只有一个面。蚂蚁的行走路径陷入了一个无限循环的怪圈,以自身为初始函数开始计算完成了一个简单的递归过程。
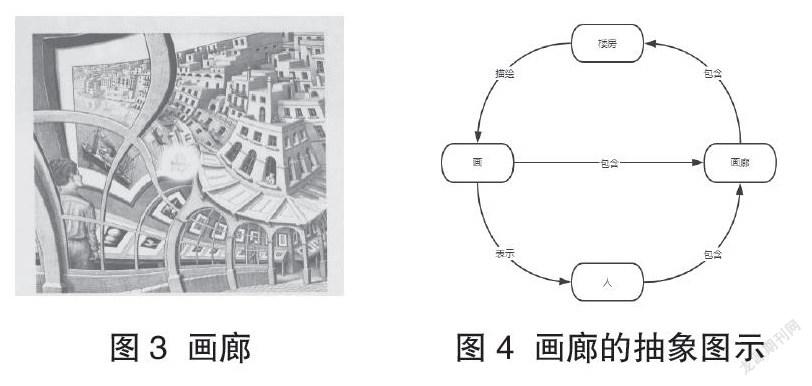
《手画手》(图2)是埃舍尔一生中最有名的作品之一,画中一只右手正在画左手的袖子,同时左手也在执笔画右手,此时正好处在快要结束的位置,达到了一种平衡。这是一种循环,就像前面的递归结构,从一个层次进入了另一个层次,然后又返回到原来的层次,进行了一种无限的循环。这幅画的空间由于手的形态,在一个二维画面中创造了一个三维立体世界。
《画廊》(图3),画廊里左下角是画廊的入口,画廊内正在进行展览。我们看到一个男青年站在一幅画前看画,其画上是一座水城,有很多楼房,有一艘船在水面行驶,最右角有一栋角楼,角楼是一间画廊的入口,画廊内正在进行展览,男青年站在那里看画……画面将整个画廊、水城楼房、看画男青年放在了一个平面中,形成了一个递归循环的怪圈。这个递归循环过程可以如图4那样抽象地表达出来。
埃舍尔创造出许多充满矛盾却令人惊叹的作品,在他的许多作品中,都通过分割、对称、循环、连续、递归等方法,把许多三维物体在二维平面上表现出来。其中的某一个设计元素,在同一个系统内循环上升或者循环下降,这个设计元素又回到了原来开始的地方。这是一个循环怪圈,也是一个自指递归的过程。
三、递归结构在图形设计中的应用
笔者从埃舍尔版画中的循环怪圈、自指递归结构中受到启发,探究其在图形设计中的应用。
首先在埃舍尔版画中进行设计灵感的获取,埃舍尔版画中使用了大量的球面来表示反射和透视的图,比如《阳台》(图5),以阳台和盆栽为中心进行突出显示,整个建筑物呈球形膨胀起来。而进行循环递归的图形设计创作,球体是最好实现的结构模型。
其次在设计元素提取上,采用解构式球形、蓝色海浪、帆船构成循环递归,设计程序使用5W1H模型。
Why:根据数学原理中的递归结构与图形进行结合进行创新设计。
What:(1)在哥德尔定理中提取递归结构模型;(2)探究递归结构在埃舍尔版画中的应用;(3)将递归结构用于图形设计实践中做出一个创意图形。
Where:用于创意图形设计。
Who:1人。
When:2020年第二学期。
How:(1)色彩定位:外部海浪天蓝色,内部采用深蓝色,帆船采用褐色与红色;(2)元素定位:解构球体模型,海浪漩渦以及帆船;(3)特点定位:通过图形体现递归结构在其中的应用。
最后在确定设计元素、主题颜色、设计程序后进行设计,如图6所示,从最底部来看帆船从漩涡开始,帆船沿海浪循环上升,最终到达最顶部的漩涡,随后又循环下降回到最底部的漩涡之中,从而形成一个递归循环的怪圈,图形也体现了渔民出海与归来的路径情景。
四、结语
本文以哥德尔不完备定理为指导,借助其推理过程中的递归函数,总结出递归结构与模型,以递归结构在埃舍尔版画中的应用作为理论支撑,探究其在图形设计中的具体应用。
递归结构能够作为一种有效的设计思维方法应用在图形、造型创造性的设计实践之中,从而形成一个灵活有趣、富有深意的创意图形。同时,递归结构(包含自我递归结构)能够完全融入艺术设计领域之中,特别是在图形、造型设计之中,进而促进艺术设计跨学科设计思维的发展。递归结构与认知结构有部分相似性,是一种“大递归中套小递归”的层次嵌套结构和过程,且当前的递归结构只能满足我们当前的需求或设计需求,随着认知需求和设计需求的不断更新,递归结构也会被更新优化,应用在图形、造型设计中也会创新优化,从而产生符合这个时代需求的创意图形。
本文只是就递归结构对图形进行创意设计,更细致的内容还有待于思考探究,但笔者相信,递归结构融入艺术设计领域中,能够为设计师从事设计实践工作时提供灵感,无论是艺术设计,还是递归结构,都能够在创新、批驳、再创新、再批驳的过程中不断走向科学与成熟。
参考文献:
[1]侯世达.哥德尔、艾舍尔、巴赫——集异璧之大成[M].严勇,刘皓明,莫大伟,译.北京:商务印书馆,1997.
[2]布鲁诺·恩斯特.魔镜:埃舍尔的不可能世界[M].田松,译.上海:上海科技教育出版社,2002.
[3]郭胜男.矛盾与悖论在条件下合理性的递归论[D].大连工业大学,2015.
[4]余劲松,陈胜利.递归对象模型在图形设计中的应用[J].包装工程,2018,39(10):74-79.
[5]郝宁湘.丘奇——图灵论点与认知递归计算假说[J].自然辩证法研究,1997(11):19-23.
[6]莫绍揆.递归论[M].北京:科学出版社, 1987.
[7]林迅.文化和艺术中的数学——M.C.埃舍尔图形创意的数学观研究[J].上海交通大学学报(哲学社会科学版),2010,18(05):37-45.
[8]孙言.埃舍尔的艺术思潮影响[J].金田,2013(05):76.
[9]紫图大师图典丛书编辑部.埃舍尔大师图典[M].西安:陕西师范大学出版社,2003.
(作者简介:董天硕,男,硕士研究生在读,曲阜师范大学美术学院,研究方向:视觉传达设计)
(责任编辑 刘月娇)

