基于克里金预测的机器人源定位方法

曹 凯，陈阳泉+，高 嵩，曹牧寒，王 坤

(1.西安工业大学 机电工程学院，陕西 西安 710021；2.西安工业大学 电子信息工程学院，陕西 西安 710021)

0 引 言

随着现代化工业的发展，各种各样的危险固体源、液体源和气体源在工农业生产、原料运输等环节发挥着至关重要的作用。在工业事故或是野外探索导致有害、有毒或无味气体释放等事件中，危险源的快速定位可以有效保护人身财产，避免大面积灾难发生。

传统固定传感器网络和移动机器人定位是目前源定位的两种主要方式。基于传感器网络的源定位方法的主要思想是预先模拟源的扩散模型，结合模型对源的参数进行迭代求解[1-4]。但该方法有两个较明显的短板，一是进行源参数求解时，对预先建立的源模型有较强的依赖。二是传感器网络的拓扑结构不能无限制扩大，无法保证传感器分布在具有代表性的区域内。移动机器人具有搜索效率高、部署成本低、安全性好等优点，更适合在复杂的环境中执行具体任务，不仅加快了搜索速度，而且避免了过于复杂的理论推导。在工厂或是野外环境中，移动机器人可以发挥其机动性实现更有针对性的搜索定位，提高了场景适应性。Rozas等作为源搜索定位领域的先行者，将基于梯度的算法在单机器人上实现，也是在源定位的第一项工作[5]。Moth算法是通过观察雄性蚕蛾跟踪雌性蚕蛾释放的信息素的行为得到的一种仿生算法[6，7]。基于编队[8，9]的源定位算法是指在不破坏队形的情况下，通过机器人之间的信息共享来寻找源的位置。概率与基于地图的算法作为源定位方法被应用，该算法称为信息趋向性算法[9]，是一种典型的贝叶斯推理方法，这类算法的特点是在不计算源强度梯度的情况下进行定位。

在实际应用场景中，基于梯度的源定位方法在实现上有很多局限性，比如算法性能低、数据传输慢等导致定位任务不准确或是定位失败。基于此本文采用一种有效的源定位方法，称为场探索，简单来说，就是在目标区域进行预先设定的路线运动，采集未知场中的场强数据，最后预测出场的分布，可直观地生成源强度分布图，该方法是一种非常有效的源定位的方法。

1 场探索理论方法

1.1 问题描述

场探索方法在很大程度上依赖于空间统计、地质统计学和地理学领域的研究成果[10-13]，该方法是基于从场中采集的数据样本进行预测，根据采集样本的协方差矩阵p生成权重，进而预测场中其它点的状态，预测过程中每一个计算的方差Ni也可以作为克里金的结果。

(1)

其中，C为在该位置处的强度值，ρ为概率密度，μ和σ2分别为均值和方差，其实高斯模型就是用高斯概率密度函数量化事物。

1.2 克里金法

克里金法假设平均值是已知的，并且对于非常大的目标区域是恒定的，但是实际情况中针对不同的源，强度的均值可能发生变化。克里金法可以从一个较小的观测子集推断出一个邻域的局部平均值，其优点在于进行预测之前不需要求出平均值，通过设置一个表示平均趋势模型的多项式，而不是从表示该邻域的恒定平均值[14-16]开始计算。

变异函数是一个连续函数，如图1所示，在空间中Z(si)，Z(sj) 任意两点之间产生协方差，已知这两点之间的欧氏距离，用hi,j∈R来表示，见式(2)

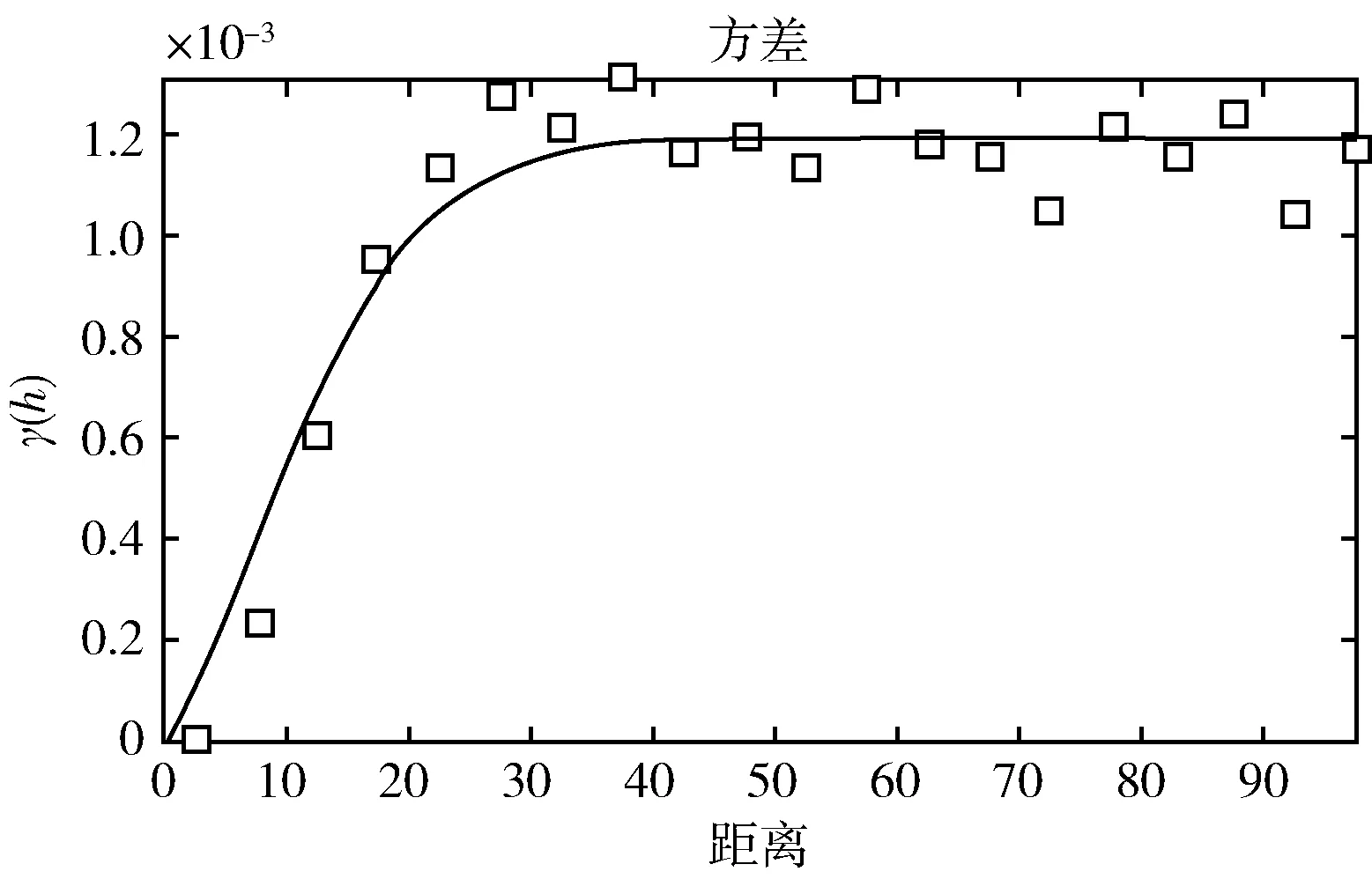
图1 变异函数模型

(2)

则在场中该点的值，即场强表示为式(3)

Z(si)=μ(si)+θ(si)

(3)

其中，θ为零均值平稳随机维纳过程，μ为场中感兴趣状态的平均值，通过场强可构建出半变异函数，由于实验过程中在垂直方向上几乎没有变化，故建立二维平面下的半变异函数，见式(4)

(4)

式中：A为目标场，即实验过程中的区域，Z(s) 表示区域中位置为s的场强值，Z(s+h) 为距离s位置的点h处的值，经验半变异函数可以表示这两个采样点位置观测值的协方差，可定义为式(5)

(5)

其中，N(h) 为观测点的个数，在场中取N个点作为样本，经验半变异函数作为场的离散模型。在目标场中采集一组样本，该组样本可以代表整个场的特性，通过计算出样本合适的方差得到个观测值的协方差矩阵，且P∈RN×N。 见式(6)，s表示为观测的点，元素Pi,j代表场中第i次和第j次观测值之间协方差，如果i=j， 则Pi,j代表第i个观测值的方差

(6)

(7)

随着在目标场中的观测值N数量增加，式(7)的协方差矩阵P与N2成正比。对于大小为180×180的场，且扫描区域占整个目标区域的30%，则P的大小为540×540的矩阵。一般情况下，维度这么高的矩阵很可能是病态矩阵，矩阵中的某一列是其它列的线性组合。高条件数意味着PP-1偏离大小相同的单位矩阵，这种逆矩阵使用LU分解便于计算。本文中使用伪逆函数计算矩阵的奇异值分解(SVD)，虽然计算较为复杂，但是在计算逆病态矩阵时误差更稳定。

对于场中的任何给定点，即观测点，可以构造一个邻近向量d0∈RN， 见式(8)和式(9)，其中包含给定点的协方差，因此dN的第k个元素将包含由点s0和第k个观测值产生的sk之间间隔的协方差

(8)

(9)

对于给定的预测位置的s0和普通克里金权重向量λ0将作为协方差矩阵的逆和邻近向量，见式(10)

(10)

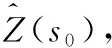
(11)

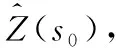
(12)

1.3 场探索

利用克里金法对场进行预测是在目标区域内每个未观测的网格单元上进行，为了从一组有限的N个观测值及其各自的位置来预测整个目标场。以下为利用克里金法预测目标场的具体过程：

(1)建立离散模型，构造一个离散的变异函数模型；

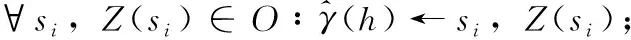
(4)构造协方差矩阵Pi,j=γ(hi,j)；

2 遍历路径

2.1 传感器数据匹配

在危险源的扩散过程中，源模型有两种形性质，即模型不随时间变化的时不变性和模型随时间变化的时变性。本文仅研究源的时不变特性，以光源为研究对象，所以设计机器人遍历方式之前，需将光照传感器信息与机器人的传感器信息匹配，应用到源定位方法中。为此，在ROS中采用rosserial协议对光照强度信息及机器人odom信息进行匹配，作为后续机器人搜索遍历时的“嗅觉”系统，实现stm32与ROS的框架。

因为本文中所使用的机器人是基于ROS的平台，ROS中利用消息、话题等进行通信，基本通信方式为TCP/IP，而通常微控制器中使用的通信方式为串行通信，如UART等，所以需要将串行通信方式通过某种方法转换为ROS中的通信方式。rosserial协议可以解决这个问题，起到了中介的作用，如图2所示，可实现ROS的微控制器和计算机之间的通信。

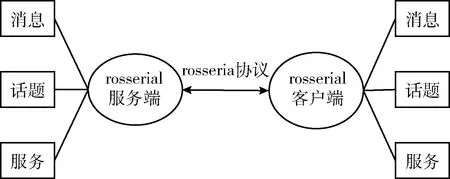
图2 rosserial协议

图2中rosserial服务端指的是运行ROS的PC，连接到PC的微控制器则为rosserial客户端。具体来说，将连接到微控制器的传感器的值进行AD转换，通过UART传输，那么计算机的rosserial服务端节点将串口发送过来的数据转换为ROS中话题。rosserial服务端作为ROS的PC上的一个节点，通过rosserial协议作为PC和嵌入式设备之间的中介。其实rosserial的服务端和客户端是以基于串行通信的数据包的形式发送和接收数据，定义时以字节为单位，包含了数据包同步和数据验证所需要的信息。

在此基础上，本文设计一个串口节点my_serial_node，如图3(a)所示，这个节点订阅talker控制节点发来的命令，将命令通过串口设备发送至移动机器人底盘，同时my_serial_node实时接收机器人底盘发送过来的传感器数据，将传感器数据封装后以sensor话题进行发布，listener节点可以订阅sensor主题。

图3 ROS与机器人串口通信过程

由于源定位过程中需要拿到机器人的实时位置，这中间存在一个问题，在采集到光照强度信息后，继续订阅机器人的位置信息会存在有延时的问题，导致光照强度信息与机器人位置信息不能一一对应。所以在获取光强传感器信息的同时，创建一个多线程节点mulpthread_node，以保证能够同时接收和发送两种信息，具体过程如图3(b)所示。该节点同时订阅由my_serial_node发布的sensor话题和odom发布的里程计信息，在里程计信息中提取出所需要的位置信息即可，最后由listener订阅mulpthread_node实时发布的移动机器人位置信息及光照传感器。

2.2 Zigzag形遍历和圆形遍历

本文从统计学角度出发，采用场探索的方法，在执行探索和巡逻等任务时常见的方法是Zigzag遍历(Z字形)和圆形遍历模式，即引导机器人通过预先定义的路径。场探索方法通过设计遍历模式，减少了由机器人自身探索带来的数据偏差，降低了机器人的能耗，使机器人可以在同等电量的情况下遍历更多的路径。

实验在指定大小为1.8 m×1.8 m的区域中进行，分为两种情形，情形一光源在目标区域一角，坐标可为(0,0)、(0,180)、(180,180)或(180,0)，本实验中将光源位置定为(0,0)。情形二光源在目标区域的正中间，坐标为(90,90)。在两种情形的基础上，为研究机器人不同数据点对后续绘制的场强分布的影响，分3种采集方式：按网格划分采集、按遍历路径采集、按区域采集。其中，机器人的采样频率为10 Hz。在Matlab中建立可视化窗口实时监测移动机器人的运动轨迹并将光照强度的大小反应在轨迹中。如图4所示，均采用Zigzag形和圆形的方式遍历区域，五角星代表光源。

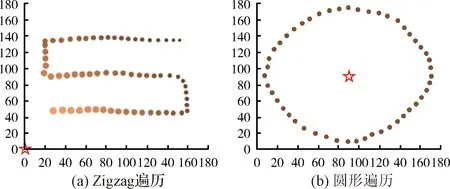
图4 遍历方式

情形一：光源坐标为(0,0)

(1)网格划分

按网格划分即在实验区域内部分别形成3×3、4×4、5×5的正方形网格，五角星为光源所在的位置，这些采样点的位置在网格线的交汇处，由于实验区域面积和机器人体积限制，故在区域内有25个采样点时即可预测出较为精确的场分布，不必继续进行网格细分。实验中，根据网格点的坐标，在Rviz可视化界面中标定网格点的坐标，将对应的Rviz中相对应的坐标点作为目标点，按顺序预先设定在机器人导航包中，使机器人按照Z字形依次遍历指定区域。在3×3、4×4、5×5网格的实验中，实时观察浓度大小变化，强度越大，颜色越亮，相应的点也越大，不符合浓度变化规律则重新进行实验。

(2)遍历路径

实验中分两种路径遍历，分别是Zigzag形遍历和圆形遍历，Zigzag形遍历是指机器人保持一定夹角或幅度做Z字形或类Z字形运动，本实验中机器人在遍历时方向夹角为90°，即每次转向保持90°不变在目标区域中遍历。垂直方向上每隔18 cm设置一个观测点，水平方向上每隔10 cm设置一个观测点，机器人整条路径中共设置39个观测点，并且起始位置坐标为(45,0)，终点坐标为(135,180)，机器人在场中做匀速运动。圆形遍历中分别设置3个半径，分别为30 cm、60 cm和90 cm，机器人的线速度v=0.2 m/s， 根据角速度与线速度的关系v=ωr可计算得出角速度大小，分别设置为ω1=0.6 rad/s，ω2=0.3 rad/s，ω3=0.2 rad/s， 机器人在目标区域中做圆周运动采集光强数据。由于机器人做圆周运动时，使用多点导航功能包需要重新设置坐标点，所以在圆形遍历时分为3次进行，在每个圆中设置均匀分布的10个观测点。

(3)区域采集

将实验区域划分为4块面积形状相同的区域，按照坐标系中的象限规则，右上角区域为第一象限，逆时针旋转分别为第二、三、四象限。实验中为了观察在不同区域中采集的数据对场分布的预测效果，在第一二象限、第一三象限、第一四象限、第二三象限和第二四象限分别采集数据，由于在第三四象限采集数据与在第二三象限采集数据后的效果相同，故只考虑其中一种情况。每个象限的大小为0.9 m×0.9 m，所以在每一个象限中分别取4个位置处的数据，实验中机器人在每个象限中做Z字形运动。当遍历区域属于同一侧时，使得机器人做U字形运动，提高整个实验的效率。当机器人在对角两个区域采集数据时，需要重新设置坐标值。

情形二：光源坐标为(90,90)

(1)网格划分

在情形二的实验中光源处于区域中央，这导致在一些情况光源可能位于机器人的遍历路径当中，故实验中手持光源至机器人上方，保证机器人能够平稳的运行，其它条件均与情形一相同。

(2)遍历路径

在Zigzag遍历算法与圆形遍历算法中，分别设置相与情形一相同数量的坐标点。为了避免机器人的位置与光源的位置冲突，分为两部分遍历，即预先设置坐标点时机器人不经过(90,90)点，在(90,108)采集结束后，手动将机器人搬至(90,72)的位置。

(3)区域采集

当光源坐标为(90,90)时，与情形一中相同，在第一二象限(同侧)采集数据与在第一四、二三、三四象限采集数据的效果相同，在第一三象限(对角)采集数据与在二四象限采集数据的效果相同，故只考虑两种情况。

3 实验及仿真结果

为模拟无障碍物条件下时不变型的危险源泄露环境，本文搭建出用于光源定位的平台，图5展示了由长方体块、移动机器人和光源组成的真实实验场景，实验在3 m×3 m的指定方形场地中进行，由于本实验中研究对象为光源，所以为了尽量排除人为因素等外界光源因素的干扰，利用简易制作的长方体块围绕在实验场地四周，所以可供机器人活动的范围为1.8 m×1.8 m，目的是在二维平面上营造一个无干扰的目标区域。机器人平台为差速式Turtlebot2机器人，配备的电脑参数为2.5 Hz主频、Intel Core i5处理器和Ubuntu16.04操作系统，装有Kinetic视觉传感器和L3G4200D陀螺仪，并外接了STM32开发板，用来光照传感器的配置。

图5 真实实验场景及Turtlebot2机器人

将机器人假设为一个点，近似认为机器人坐标和传感器坐标是相同的，并且所用的光源是均匀扩散的。实验中机器人的运动速度以0.2 m/s匀速遍历，经多次测量实验中光源的峰值约为2283 lx。实验中存在有以下3个影响因素：一是传感器的精度；二是机器人的定位不准，遍历时机器人可能会偏离预先设定的路径和坐标点；三是实验平台中的障碍物是手工制作，可能存在实验中整个目标场不是方形区域的情况。为避免以上3个因素对实验产生的偶然结果，每组分别进行20次实验，将偏差较大的实验舍弃。通过对数据的统计后利用克里金法预测场的分布，及绘制出等值线图，可以直观地显示出不同情形下光强的分布结果和源的大概位置，以下为两种情形中的实验结果。在20次实验后，光强数据被存放在csv文件中，对每个点的数据求均值后作为绘制等值线图时的数据。

情形一：光源坐标为(0,0)时的仿真结果：

(1)网格划分

如图6及表1所示，对目标区域网格化后，在场中的9个观测点采集光强信息，预测得到源的位置大致在(41.86,42.47)处，在该区域附近形成局部最优，定位效果较差。采集16个观测点时，在(20.44,21.25)也形成局部最优，整个场的分布更接近于光源扩散模型。在此基础上，增加为25个观测点时场强分布可基本预测出光源所在的位置，坐标为(13.68,14.52)，相比于其它两组实验误差最小，主要原因是实验中机器人的尺寸较大，在场中采集更多观测点的值会导致数据重复以及在某些位置难以采集到数据。图7记录了20次实验中预测出源的位置与实

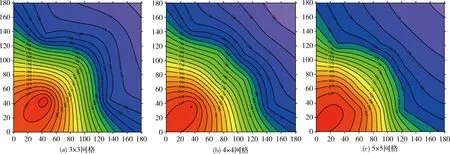
图6 情形一网格划分等值线

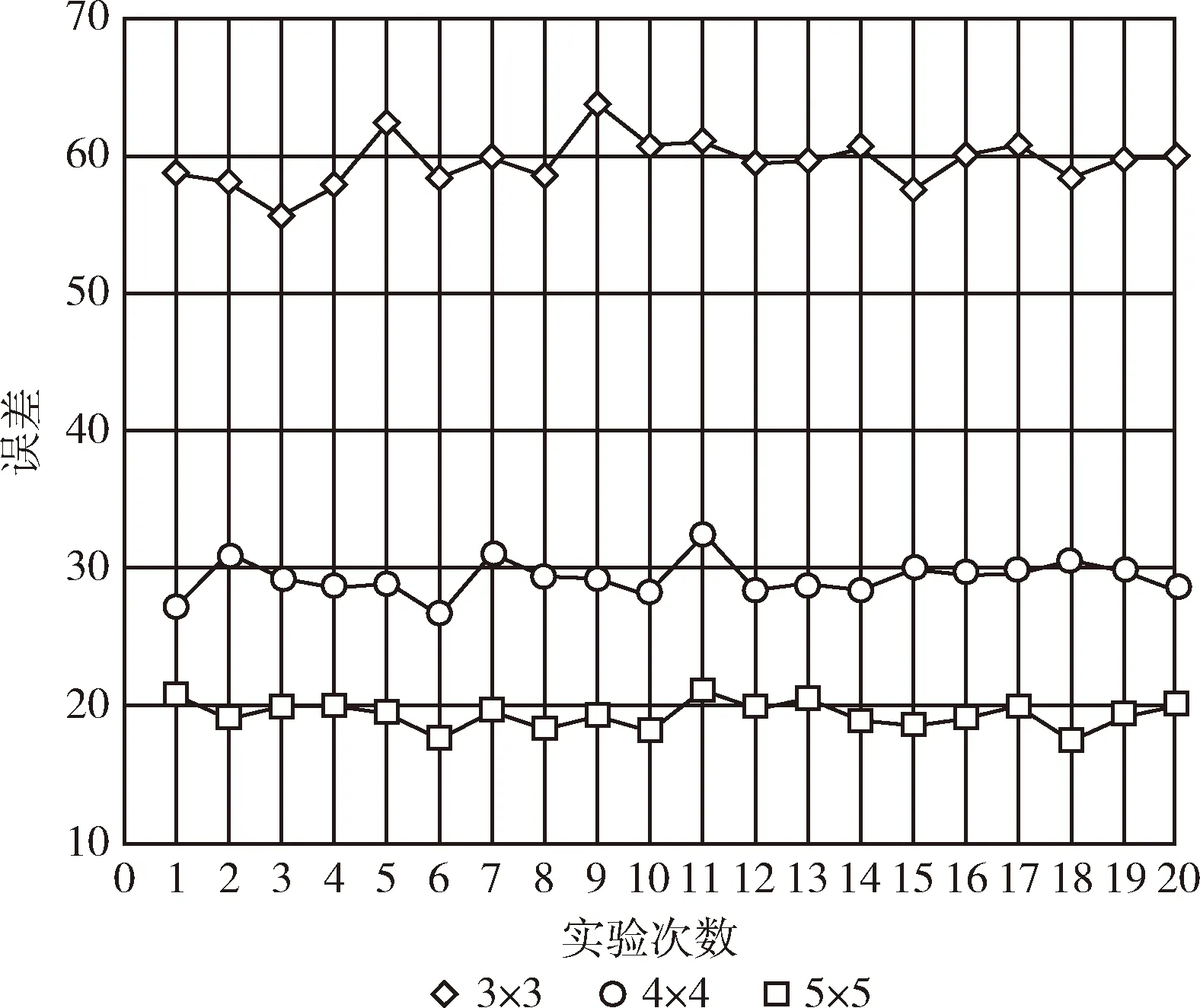
图7 预测源位置与实际源位置的误差

表1 实验数据统计

际值的差值，实验中误差变化范围都稳定在10 cm内。仿真结果显示，在场中的观测点数量越多，预测的结果也越准确，误差也越小。

(2)遍历路径

图8为两种遍历方式预测的场分布。

图8 情形一遍历路径等值线

如图8及表2所示，靠近光源位置处的圆形遍历的预测效果更符合光源的分布模型，但是在远离光源的一侧，虽然有着偏向光源的大致趋势，但这时Zigzag形遍历方法更准确，绘制出的等值线图更平滑。从整体场分布来看，采用圆形遍历预测源的位置的误差较Zigzag形遍历更小，效果更为明显。图9记录了20次实验中的Zigzag形遍历和圆形遍历的源位置误差，显示误差均在20 cm之内，所以在场中的遍历路径对于预测的结果影响不大，但是预先设置的路径必须合理有效，避免出现在某一位置重复采集的问题，最大化机器人的效率。

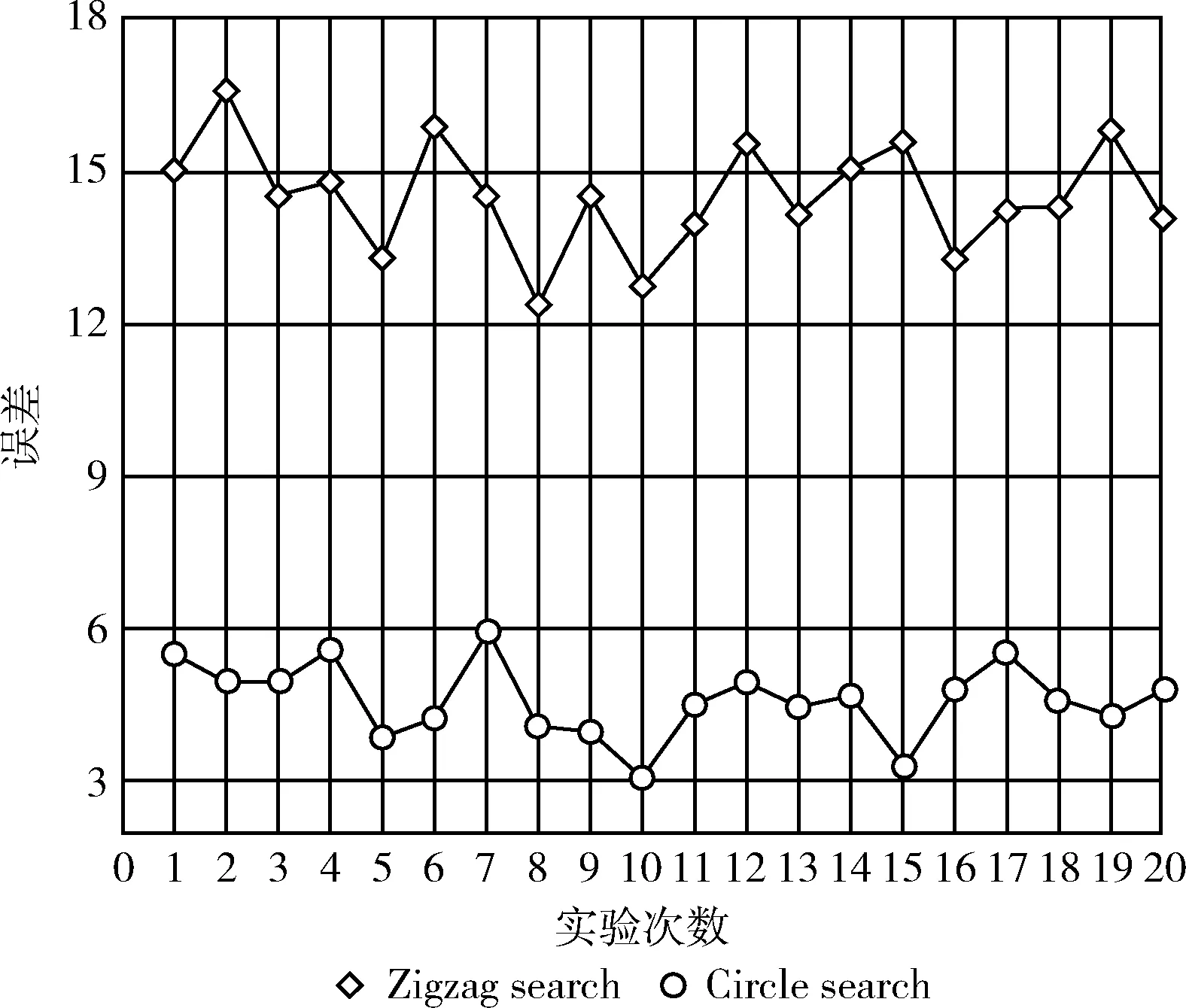
图9 预测源位置与实际源位置的误差

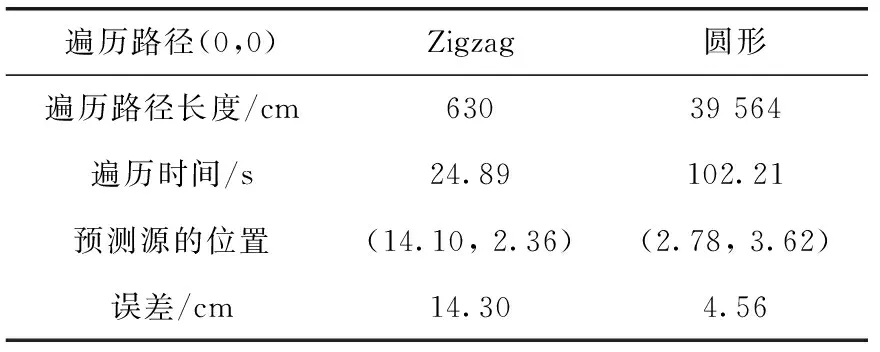
表2 实验数据统计

(3)区域采集

图10及表3为5种采集方式预测的结果。

表3 实验数据统计

图10 情形一区域采集等值线

图11记录了20次实验的情况，采集位置在一三、二三和二四象限时，等值线图符合光源分布模型,误差小。其它两种情况下，存在5处局部最优值，可能是采集区域与存在极值处的区域相距较远，故最好采用对角区域遍历的方式采集信息。

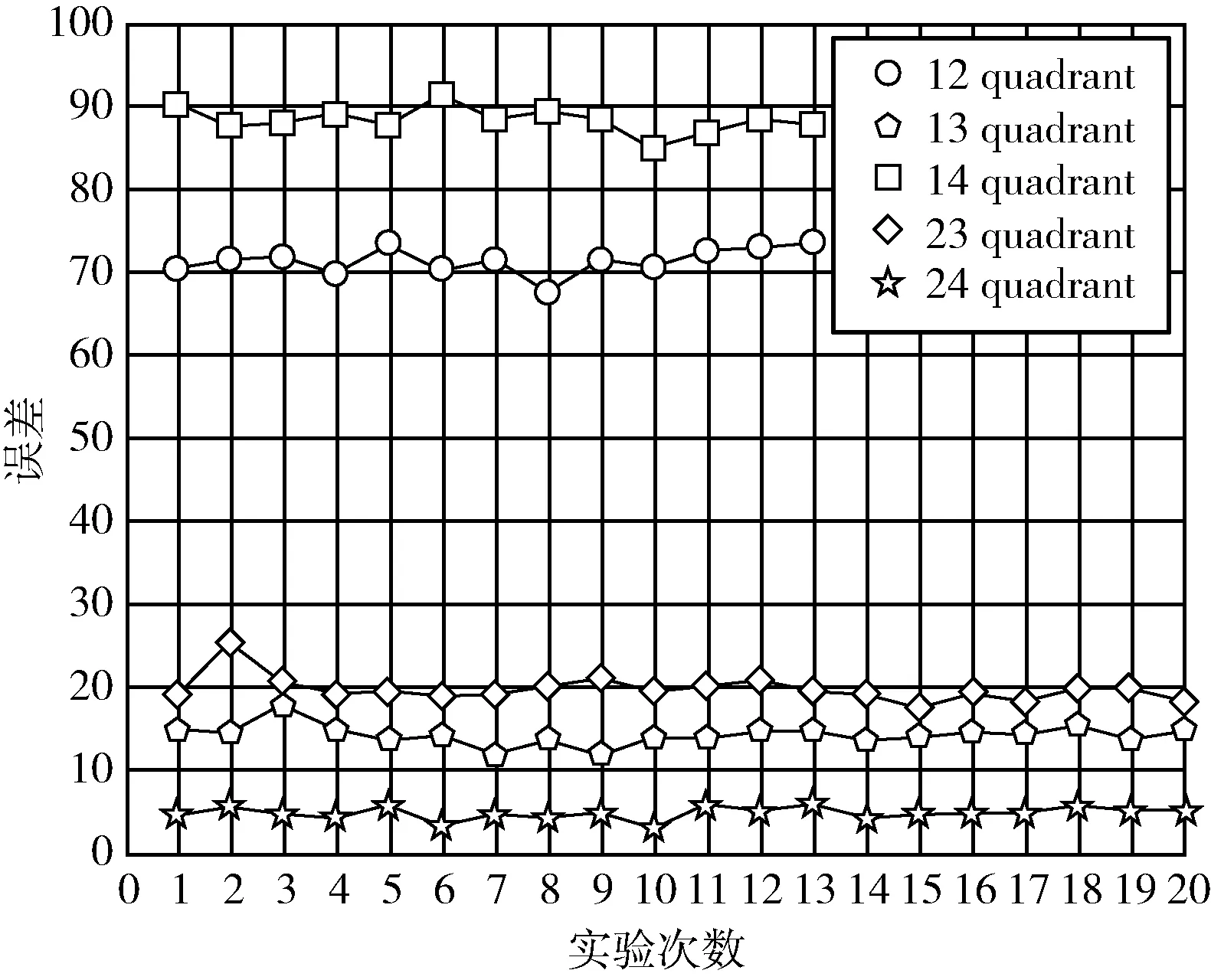
图11 预测源位置与实际源位置的误差

情形二：光源坐标为(90,90)时的实验结果：

(1)网格划分

考虑到光源与机器人尺寸的问题，预先设置的目标点均增加和减少5 cm，即以(90，90)为原点，5 cm为半径的圆周上，均匀取4个点的数据求均值作为光源处的光强值，如图12及表4所示。

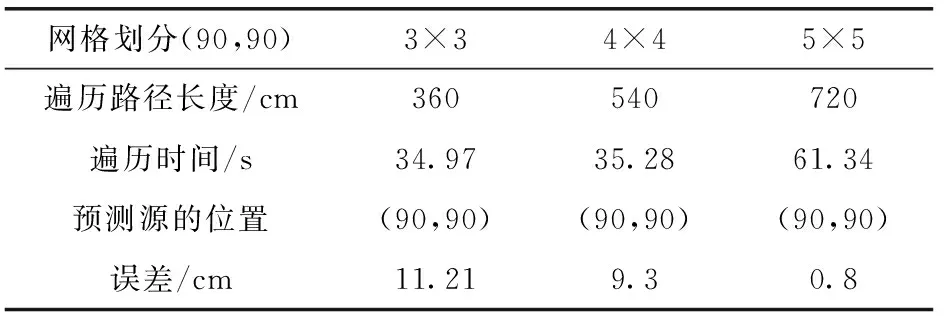
表4 光照强度数据统计

如图12(a)，场中设置9个观测点时，光源附近半径为30 cm的区域中场的分布符合光源的高斯分布模型，但是在如(30,30)位置处出现局部最优，主要原因可能是预先设置的坐标点较分散，导致在该点附近有数据缺失，使预测时场的误差较大。相比之下，图12(c)中网格点的数量增加可以减少预测时的误差，定位效果较好，在光源附近预测场分布的范围扩大。在此情况中预测光源位置就是实际源的位置，并且在场中网格点的数量越多，则预测的场的效果越接近真实场的分布。

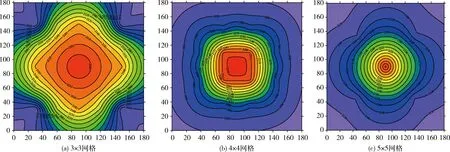
图12 情形二网格划分遍历等值线

(2)遍历路径

如图13及表5所示，利用Zigzag方法遍历比圆形遍历的效果差，可能是机器人运动时的定位不准，偏离了预先设定的坐标位置。利用场探索的方法预测场分布时，即采用圆形遍历的定位精度更高，等值线图更符合高斯模型，达到了预期的效果。

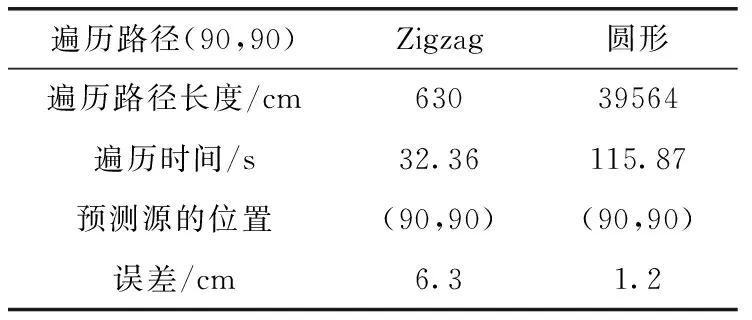
表5 实验数据统计

图13 情形二遍历路径等值线

(3)区域采集

如图14及表6所示，该种情形只能预测出光源位置的一个大致范围，并且该区域较大，定位精度低。在真实危险源定位的环境下，区域采集的情形可能需要利用其它方法，比如深度学习的方法，通过训练数据集得到更准确的数据，本文采用的方法也只是在无障碍物情况下的场景，在有建筑物等的隔档时在全局场景中遍历可以得到更为有效的数据，得到的结果也更理想。图15记录了20次实验中两种情况时的源位置误差，虽然预测场的分布不能直观地表示出真实光源的分布，但预测后源的位置与真实源位置误差范围也在10 cm内。

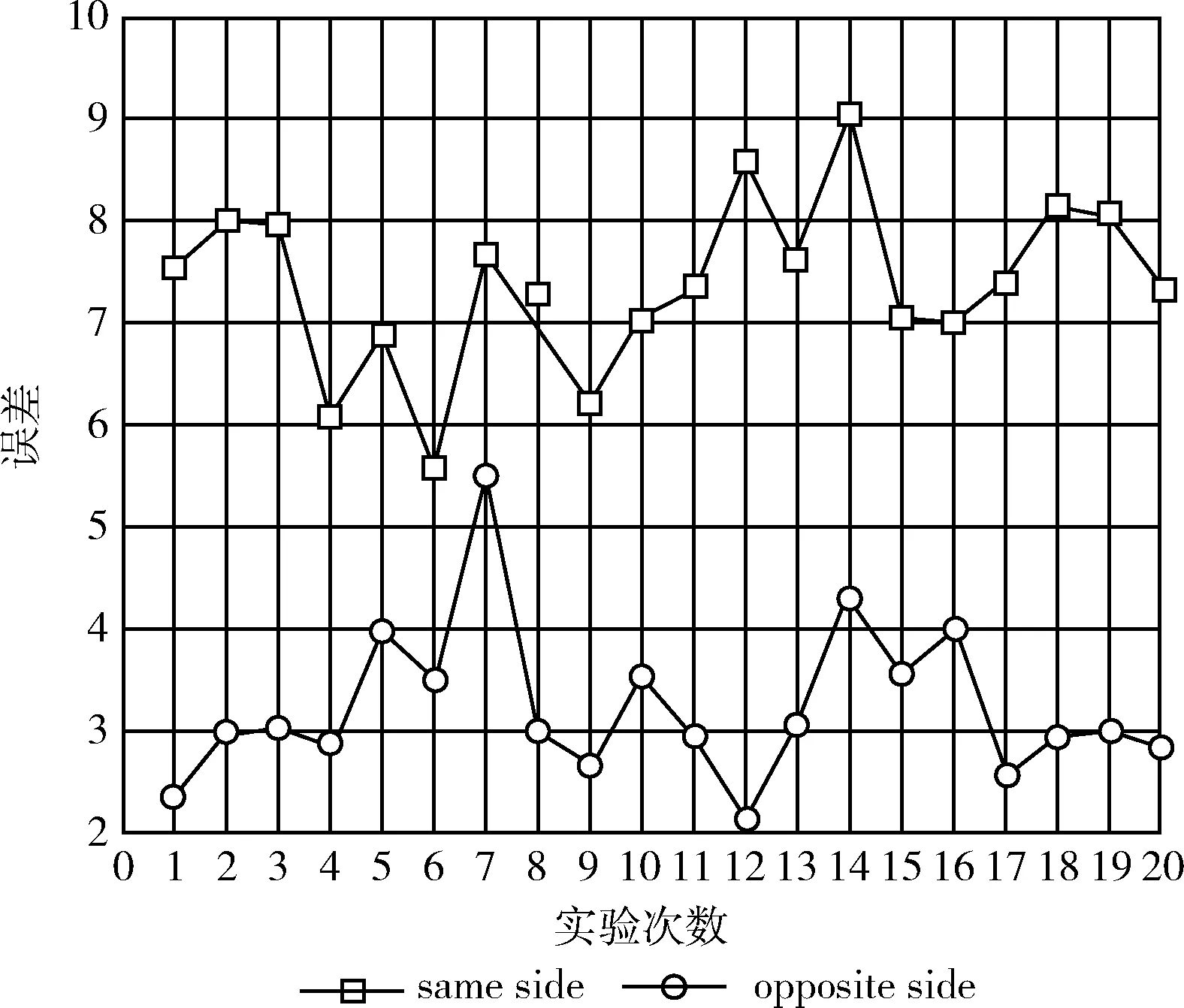
图15 预测源位置与实际源位置的误差

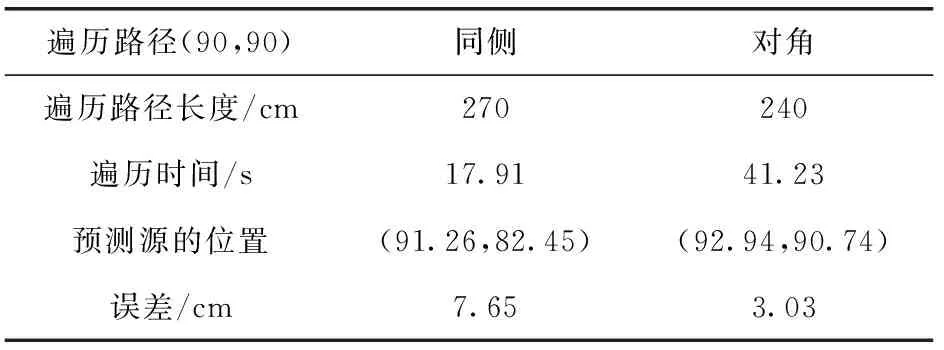
表6 实验数据统计

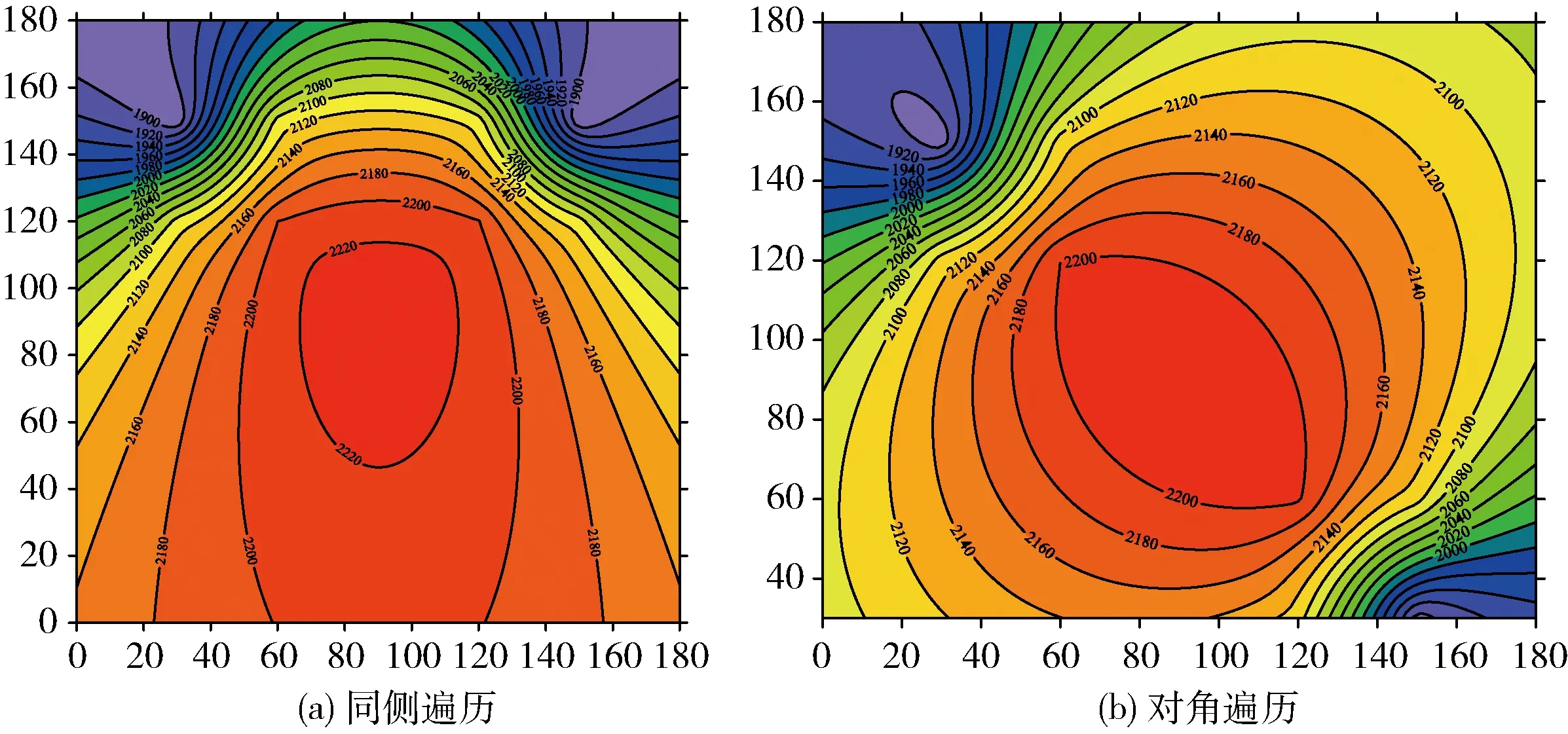
图14 情形二区域采集等值线

综上所述，在情形一中，采用区域采集的方式定位误差小，同时用时和路径长度都较短。具体表现为在一三象限和二四象限时信息的获取，分析原因可能是在这两个象限的跨度较其它几种方法更大，所以机器人在获取环境信息时遍历区域的面积占比更大，更形象地表现出该区域场的特征。在情形二中，采用遍历路径的方式定位误差极小，具体表现为圆形遍历方式。虽然在遍历路径长度和用时上都较多，但是预测出场的分布更符合高斯分布，符合真实的光源分布。故在实际场景中，选择圆形遍历的方式进行源定位任务会得到更好的效果，主要是由于圆形遍历可以扫描占比更大的区域，获取的信息也更能代表出场的特征。

4 结束语

本文提出了一种用于源定位的场探索方法，与传统的基于梯度的算法相比更为突出。传统的源定位方法虽然在仿

真容易建立，但是在机器人上实现时基于梯度的算法性能低下或是数据传输慢导致机器人延时相应，发送给机器人错误的场信息。与基于梯度的算法相比，场探索方法结合了统计学中的数据处理方法和场的分布特点，优点在于不需要建立复杂的动力学模型，避免了复杂的数学建模过程，利用克里金法对场中的每个单元网格进行预测，提高了数据的稳定性。同时减少了机器人随机搜索带来的能耗问题，简化了传统的基于梯度的源定位方法对于算法的有效性和机器人的性能的高要求。通过设计机器人的遍历方式并搭建出真实实验场景，验证了该方法可以对目标场的分布预测的可行性，成功预测出场的分布，提高了源定位方法的灵活性与实用性。

在未来的工作中，需要解决的是机器人动态绘制场分布的等值线，也可以称为实时绘制问题。另一方面，在机器人的底层控制上需要更精准的遍历搜索，实现更准确的数据获取，从而得到更真实的场分布。进一步地，在研究达到很好的效果时，将扩展至三维空间进行研究。