正弦脉宽调制波通用谐波计算与分析方法

严海龙

(福州大学电气工程与自动化学院，福建 福州 350116)

1 引言

正弦脉宽调制(sinusoidal pulse width modulation，SPWM)[1-7]技术目前已经在实际中得到非常广泛的应用。SPWM信号的生成与控制主要有硬件法和软件法两大类[8]。硬件法，顾名思义，是采用专用集成电路，成本相对较高；软件法则是通过微处理器实时生成SPWM波。早些年人们是采用微机或单片机来计算，由于受处理器运算速度的限制，计算的速度和精度往往无法同时满足，现在具有高速运算功能的数字信号处理器(digital signal processor，DSP)的出现，尤其是电动机控制专用型DSP的出现，使得这一问题轻松得到解决。软件法生成SPWM信号的具体实现有很多方法，比如采样型SPWM法、谐波消去法、等面积法等，尤其是采样型SPWM法比较普遍，其中包括自然采样法、对称规则采样法、不对称规则采样法[9]。自然采样法因为涉及到求解超越方程，所以一般只作为理论指导。不对称规则采样法较对称规则采样法的采样时刻更接近于自然采样法，使得其生成的SPWM波更加接近于正弦波，即谐波含量更低，因此在实际中得到更为广泛的应用。然而，不对称规则采样法在每个载波周期内要采样两次，是以采样次数多、占用微处理器内存资源大和实时性相对较差为代价，来获取较对称规则采样法谐波含量低的优点[10]。

如果想要研究出性能更好的新型SPWM技术，谐波含量的定量计算与分析则是必不可少的，这是评估新技术优劣的一个重要指标[11]。为此，本文基于MATLAB数值计算和傅里叶级数，提供了一种采样型SPWM波的谐波通用计算与分析方法，并以不对称规则采样法SPWM波的生成及其谐波分析为例，验证了该方法可以为SPWM新技术的研究提供参考作用，如文献[10-11]等中的新技术的研究。最后，本文通过对占空比为30%的方波的谐波计算，验证了该方法也可以作为任意周期性PWM波的谐波通用计算工具。

2 采样型SPWM波的MATLAB生成方法

图1所示是不对称规则采样法生成SPWM电压波形的原理示意图，正弦调制波函数Um·sinwt，其中Um是正弦波的幅值，w是正弦波的角频率，且w=2πf，f为正弦波的频率，正弦波周期T=1/f。 高频三角载波的幅值为Uc，频率为fc，周期Tc=1/fc。M=Um/Uc称为调制度或调制比，即正弦调制波峰值与三角载波峰值之比；N=fc/f=T/Tc称为载波比。本文以不对称规则采样法SPWM波为例，分析所提出的谐波计算方法。如图1所示，不对称规则采样法既在载波的顶点对称轴位置采样，又在载波的底点对称轴位置采样，也就是在每个三角载波周期内采样两次，比对称规则采样法多了一倍。

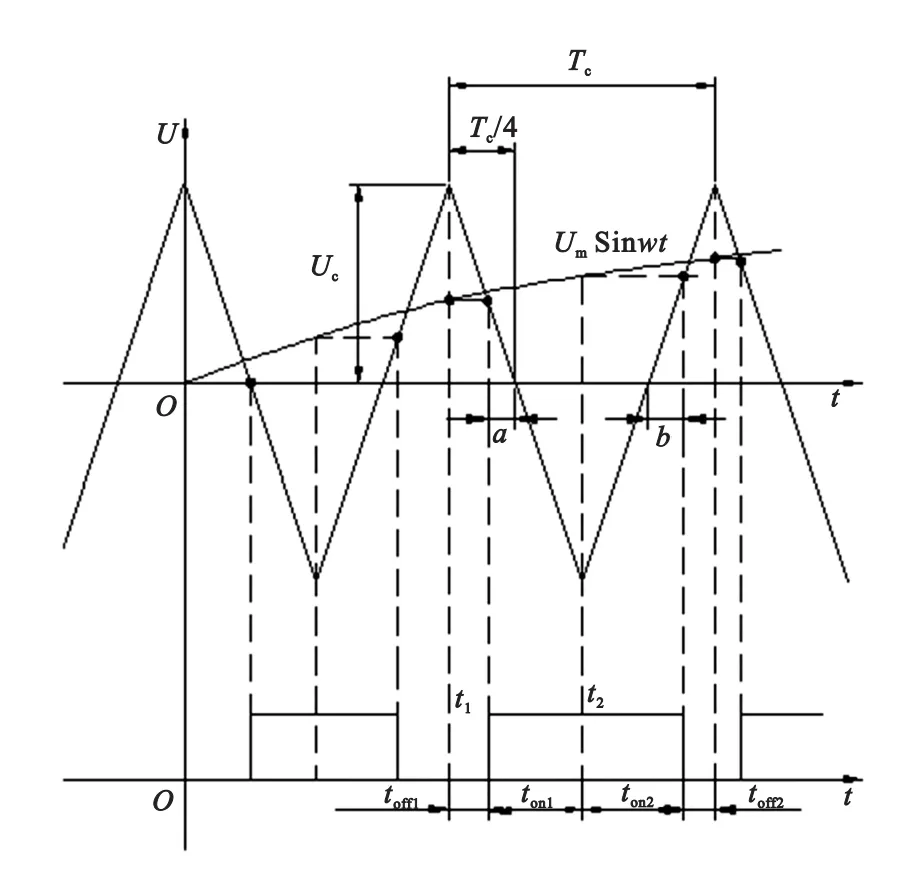
图1 不对称规则采样法SPWM原理图

由参考文献[8]可知，两种采样法的A相脉宽计算公式分别是:

对称规则采样法:

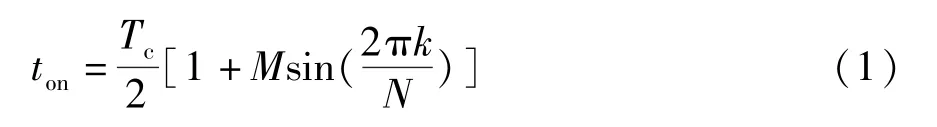
不对称规则采样法:

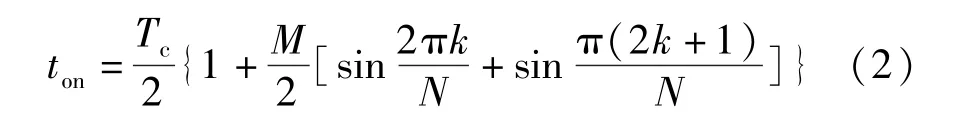
式中，k=0，1，2…N-1；M为调制度；N为载波比。

图2所示是基于MATLAB的SPWM电压波形生成主程序流程图，利用数组思维计算各相电压及生成电压波形，程序的关键点在于两个数组t(时间)和Ua(A相电压)长度必须一致，这里采用t与数组序号i同步增长的方式保证两者数组长度一致。

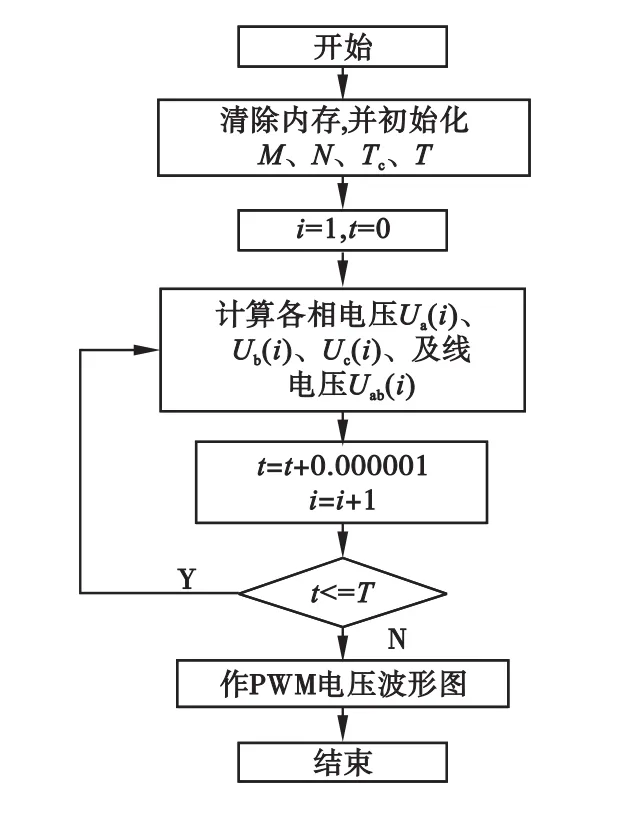
图2 SPWM电压波形生成主程序流程图

A相电压Ua(i)的波形生成子程序流程图如图3所示，B相电压Ub(i)和C相电压Uc(i)的波形生成子程序与A相类似，即在计算关断区间Toff1和导通区间Ton时，B相在A相的基础上减去2π/3相角，C相在A相的基础上加上2π/3相角即可。

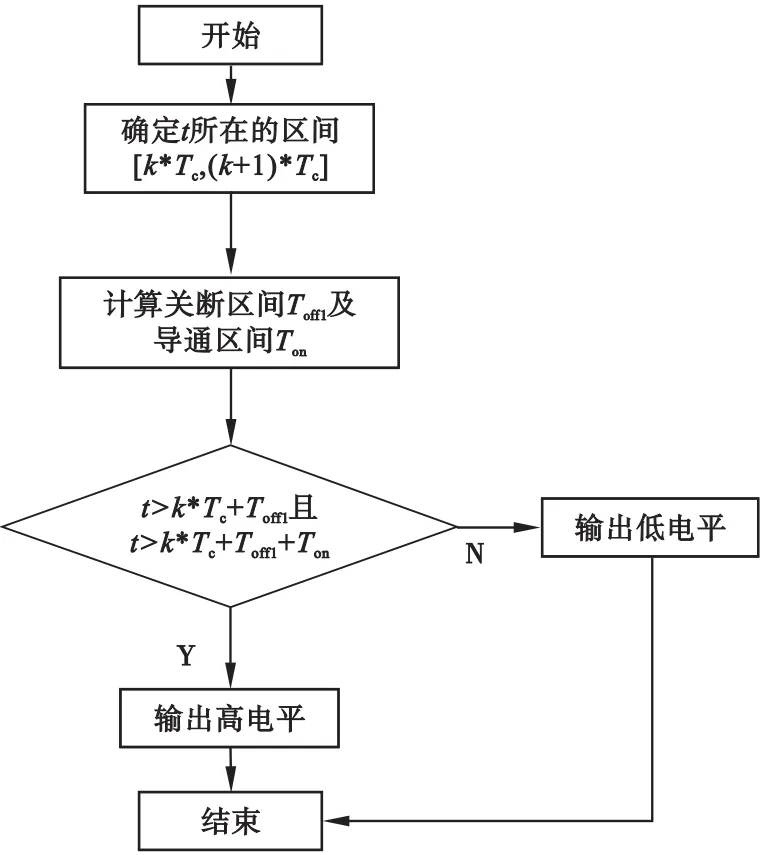
图3 A相PWM电压波形生成子程序流程图

设逆变器前端母线电压为500V，上述图3对应的不对称规则采样法PWM波形生成参考程序如下:

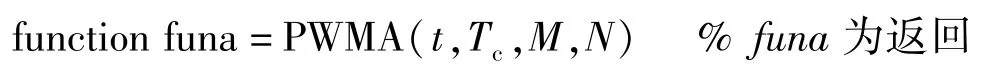
该程序的关键在于利用向零取整函数fix计算载波序号k值，并说明t在区间[k*Tc，(k+1)*Tc]。

取M=0.8，N=15，f=50Hz时，利用图2和图3所述方法生成的不对称规则采样法SPWM波形见图4所示。

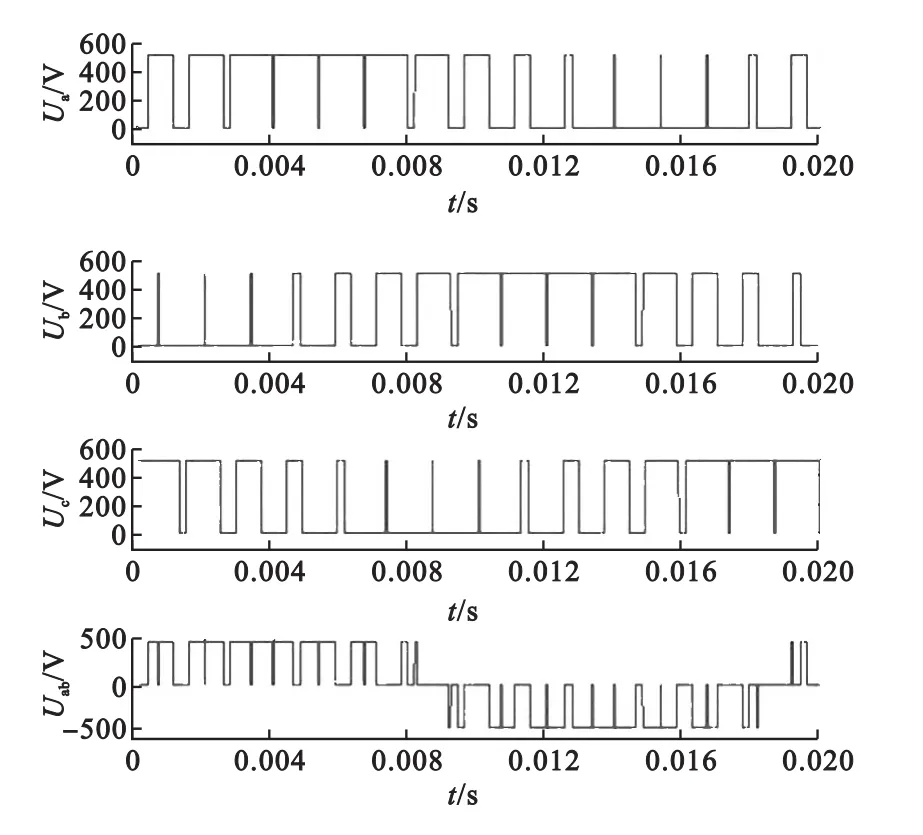
图4 不对称规则采样法PWM电压波形

3 谐波含量的计算与分析

3.1 各次谐波含量的计算

本文基于傅里叶级数，将谐波含量的计算具体详细化，并且提供相应的MATLAB软件编制通用方法。

如果周期性线电压函数Uab(t)的周期为T，频率为f=1/T，基波角频率w=2πf，Uab(t)=Uab(t+T)，那么Uab(wt)可以分解为无限项三角级数——傅里叶级数，即如式(3)～(7)所示。

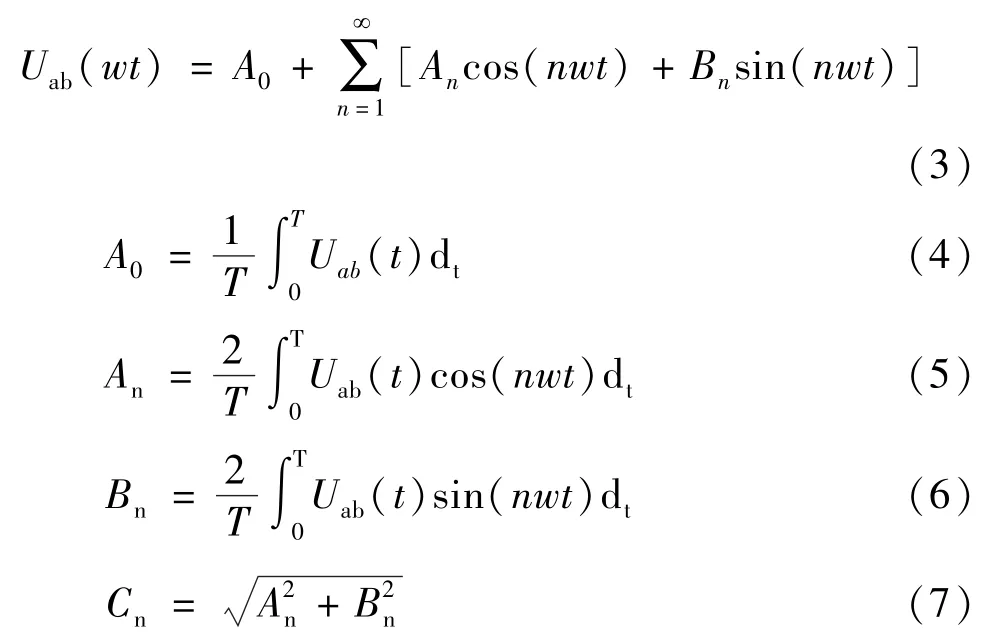
式中，A0是直流分量，An是n次谐波余弦分量，Bn是n次谐波正弦分量，Cn是n次谐波幅值。n=1时，C1是基波幅值。

图5是采用傅里叶级数及MATLAB数值计算的各次谐波含量计算主程序流程图。图中M为调制度，N为载波比，T为调制波周期。

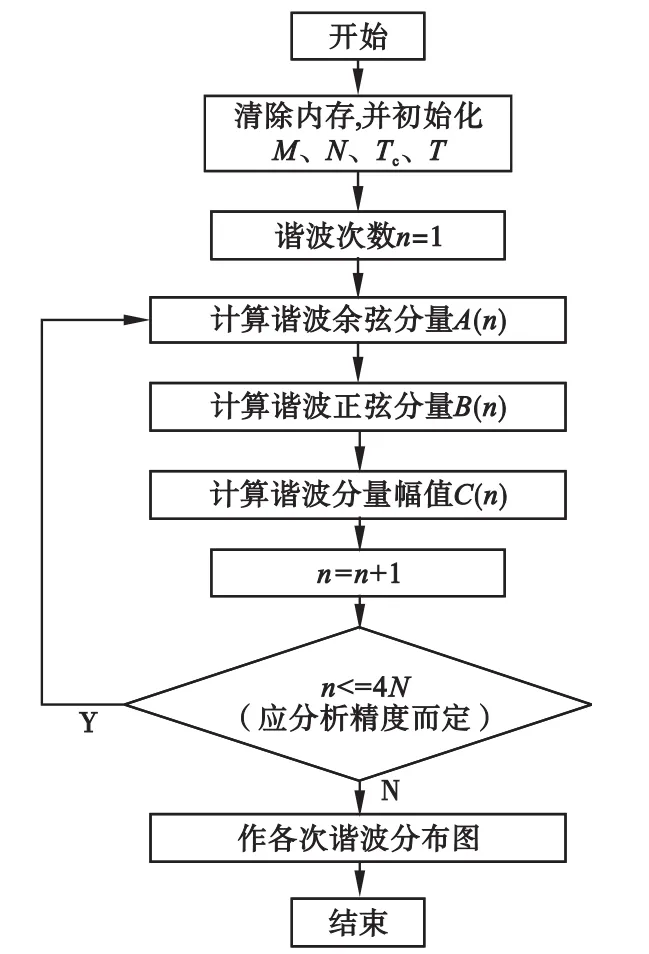
图5 各次谐波含量计算主程序流程图

以不对称规则采样法为例，A相电压的谐波余弦分量计算子程序可参考如下，B相电压的计算类似，在关断时间和导通时间的计算式上与A相滞后2π/3。如此A相与B相的谐波余弦分量之差便为线电压Uab(t)的谐波余弦分量，而线电压Uab(t)的谐波正弦分量的计算亦是类似。

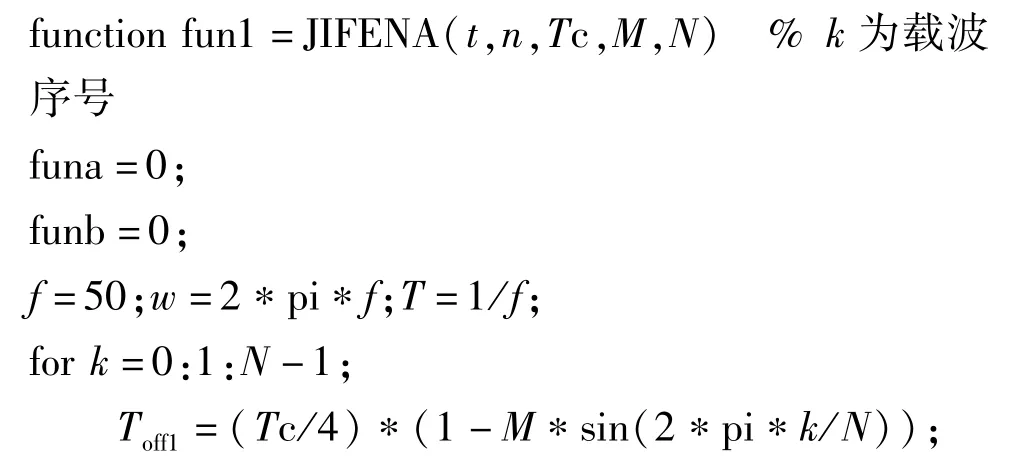
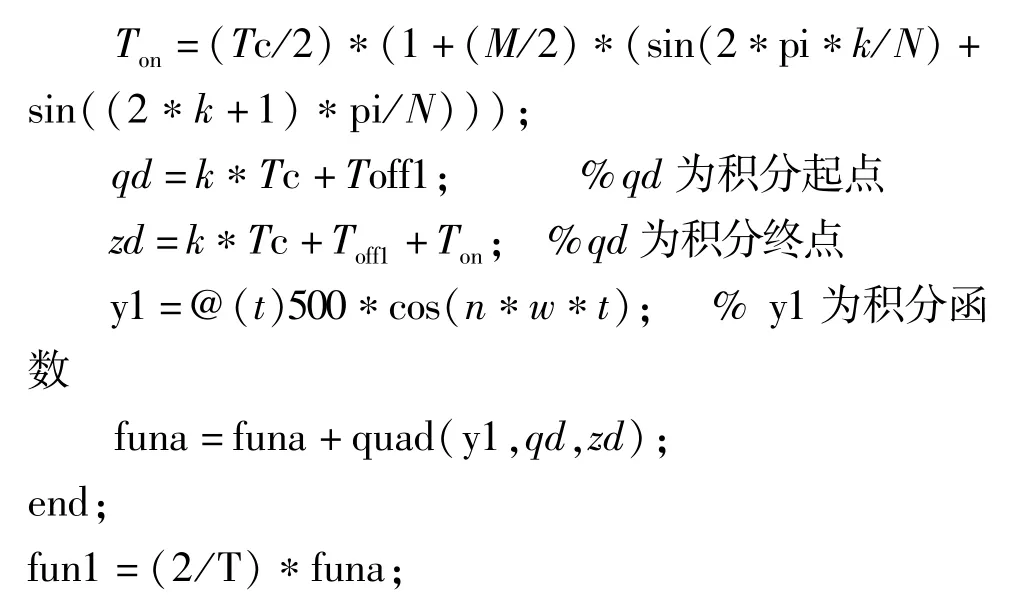
以上关键思维有三点:一是采用了分段处理，即每个载波期间各自积分，分段计算后再叠加；二是分相处理，不直接计算线电压的余弦分量，而是由各自计算A相和B相的余弦分量后相减所得。三是采用＠(t)将多个变量函数的自变量限定为t。

采用图5方法，不对称规则采样法生成的线电压谐波分布情况见图6所示。

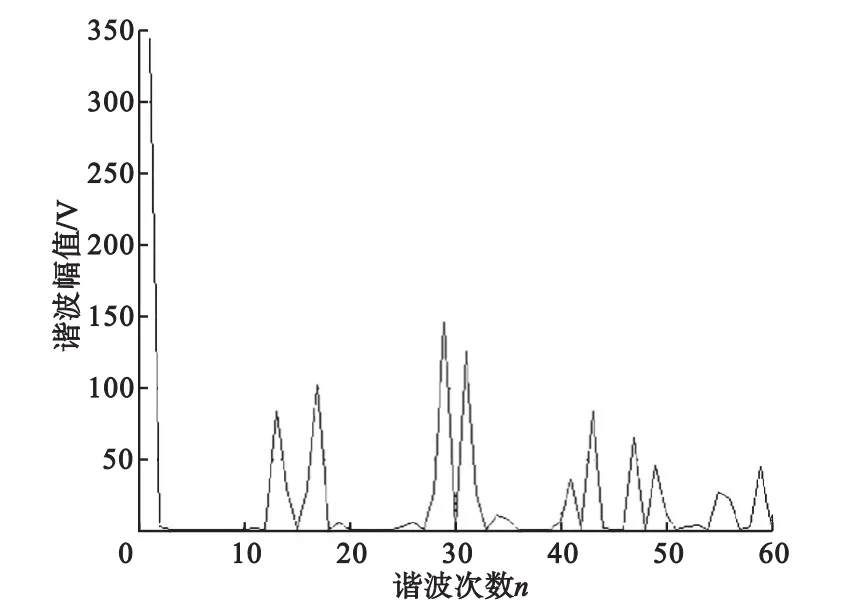
图6 不对称规则采样法线电压谐波分布情况(N=15)

计算结果表明，4N次(N为载波比)以下谐波中，含量比重较大的是N±2、2N±1、3N±2、3N±4次谐波，即载波比及其倍数附近次数的谐波。改变载波比N，亦能得到相同的结论。4N次及以上高次谐波可在交流调速时被电机自身漏感滤波掉，可根据计算精度要求不予分析。对称规则采样法生成的线电压谐波分布情况分析与不对称规则采样法的类似，只要在涉及到计算导通时间时分别采用上述式(1)和(2)。

3.2 总谐波系数的计算

交流调速系统中，为了比较各种采样法SPWM波输出线电压的总谐波幅值，即评价两者输出电压波形的质量，可以引入总谐波系数THD:

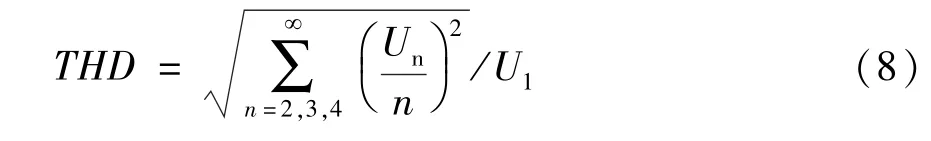
式中，n是谐波次数，Un为谐波幅值或有效值，取幅值时即为式(7)中的Cn，U1为基波幅值，即C1。

THD的计算流程图如图7所示，采用此方法计算对称规则采样法和不对称规则采样法生成的的线电压波形THD比较见图8。由图8可定量验证不对称规则采样法较对称规则采样法生成的SPWM波谐波含量确实更低，即更加接近正弦波。类似的，我们可以采用本文的方法计算分析其他PWM波的谐波情况，在此基础上，也可以为探索新型SPWM技术提供方法依据。

图7 总谐波系数THD的计算主程序流程图

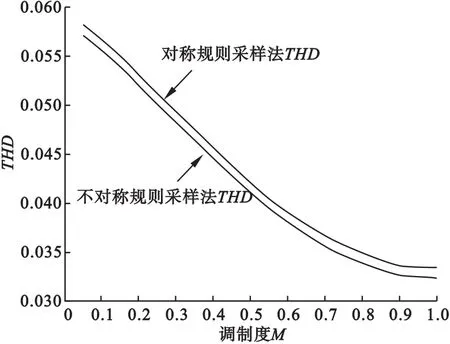
图8 采样法SPWM线电压THD的比较(N=15)

4 其他PWM波谐波分析的通用性验证

以占空比为30%的PWM方波举例说明，采用本文的方法或思路可以计算出该PWM波的各次谐波分布情况，结果为:在60次谐波以内，除基波外，比重较大的谐波有29次、49次、58次。采用图7的方法计算该PWM波的THD值，结果见表1所示，忽略高次谐波的影响，该 PWM波的 THD值为0.3075。

表1 占空比为30%的PWM方波THD值计算

5 结论

交流调速系统中，传统采样型SPWM技术因为采样次数的不同各有优缺点，为在原有SPWM技术的基础上研究新型SPWM逆变技术，谐波含量的计算与分析是必不可少的，这是评估SPWM技术优劣的一个重要指标。本文基于MATLAB数值计算和傅里叶级数，提供了一种PWM波的谐波通用计算与分析方法，并重点以不对称规则采样法为例，给出了详细的谐波计算过程以及相应程序段或关键思维点。文中不对称规则采样法、对称规则采样法以及方波三种PWM波的谐波计算结果，验证了该方法可以作为SPWM新技术研究的辅助工具，也可以作为任意周期性PWM波的谐波通用计算工具。