基于混合Copula函数的风电机组异常识别方法

杨天玥，赵丽军，徐健，厉伟，张国军

(1.沈阳工业大学电气工程学院，辽宁 沈阳 110870；2.华能辽宁清洁能源有限责任公司，辽宁 沈阳 110015)

1 引言

风电机组的功率曲线是风电机组控制系统设计的重要依据，也是评估风电机组性能及发电能力的重要指标[1-2]。在风电机组控制系统中，功率曲线直接影响控制策略以及控制过程中参数的调整。因此，功率曲线异常识别是十分有必要的。

风电机组功率曲线异常识别及故障诊断是当前的研究热点，国内外学者已开展相关工作并取得了一定的研究成果，其中风电机组功率曲线数据识别的代表性成果有:文献[3]通过采用分组最优方差算法成功识别出功率曲线下方堆积型异常数据，但该算法无法识别功率曲线上方堆积型异常数据；文献[4]基于Copula函数建立概率功率曲线模型，基于SCADA数据对风电机组进行故障诊断，模型可以对风电机组叶片、偏航系统及变桨系统进行早期故障预测，但输入变量只有风速，无法准确描述风电机组整体运行情况；文献[5]通过建立功率曲线的非线性模型来识别异常数据，但是需要大量的正常数据作为样本，否则会使模型误差变大，这将导致异常数据识别速度变慢；文献[6]假设风速、功率的概率密度函数服从正态分布，提出了基于3δ法则的异常数据识别与清洗方法，但该方法与实际风电机组运行中风速功率的概率密度函数不符，其适应性及异常数据识别效果欠佳；文献[7]通过加权最小二乘支持向量机回归模型建立的功率曲线模型检测风电机组的异常运行，利用在线监测不断更新模型并剔除异常点，结果表明该模型准确性高于其他模型。

针对传统的异常数据识别算法中存在的问题，本文提出基于Copula函数的风电机组异常识别方法，首先，对风电机组正常运行不同工况下功率曲线的影响因素进行相关性分析，判断出对功率曲线影响大的特征参量；其次，通过二元概率分布函数得到了风电机组功率曲线上下边界，对于上下边界外的可疑点进行时序分析；最后，通过计算可疑点与正常点之间各特征参量的欧氏距离判断可疑点是否为异常点，从而确定风电机组故障位置。基于SVM线性回归，采用某风电机组的实测数据进行仿真验证，结果表明混合Copula函数模型能够准确的识别异常数据，具有较强的实用性。

2 功率曲线参数相关性分析

将风电机组运行中最大风能追踪阶段划分为工况B，发电机转矩控制阶段划分为工况C，定速变桨控制阶段划分为工况D，如图1所示。分别对各工况下的风速-功率、风速-叶轮转速、风速-桨距角、风速-偏航角进行Kendall相关性分析，结果如表1所示，当功率曲线出现异常时大概率是相关性较大的变量异常导致。由表1可见，工况B下，风速-功率、风速-叶轮转速、叶轮转速-转矩、叶轮转速-有功功率、转矩-有功功率相关系数均很高；工况C下，转矩-有功功率相关系数最高；工况D下，风速-桨距角相关系数最高。三个工况中，风速-偏航角相关系数最低，说明偏航角与风速相关性较小。相关性分析所得结果与风电机组的工作特性相吻合。因此，本文着重于风速-功率、风速-叶轮转速、风速-桨距角对风电机组运行状态的影响进行分析。

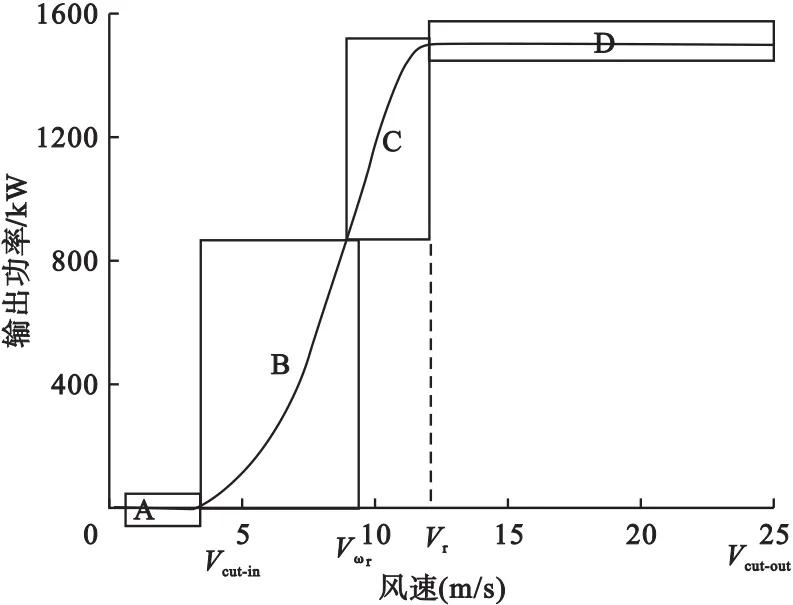
图1 功率曲线工况划分图

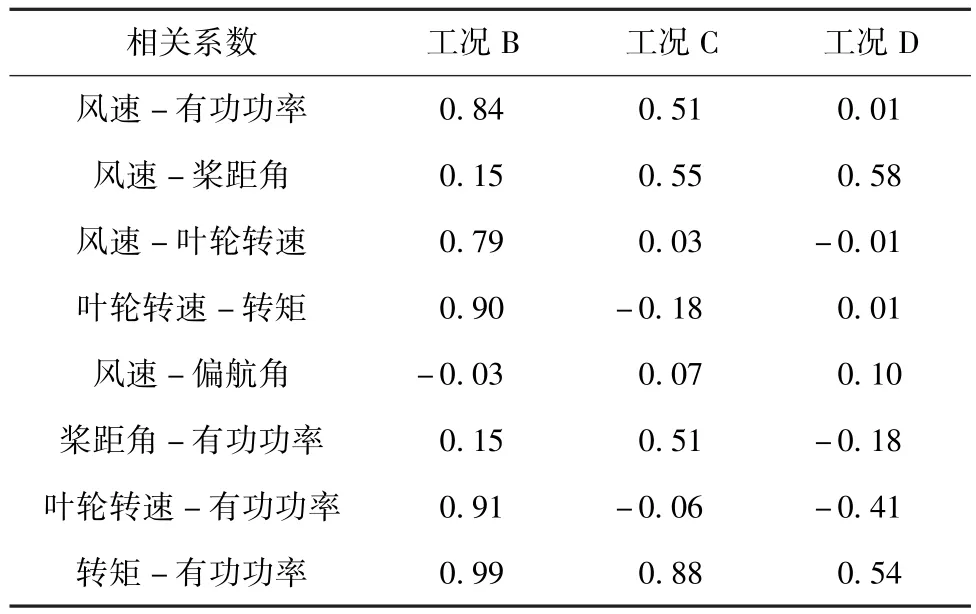
表1 相关性分析

3 异常数据识别模型

风电机组的功率特性除取决于风电机组的性能外，还取决于气象环境条件以及风电机组在风电场中的排布等[8]。风电机组在设计时假定空气密度为常数，实际上空气密度会随地理位置不同而不同，空气密度所造成的误差会在风速中放大[9]，因此每台风电机组正常运行的输出特性也不尽相同，所以直接使用风电机组厂商提供的功率曲线对异常进行状态检测存在较大的故障误报风险，需要基于每台风电机组的实际运行数据来进行功率曲线建模，为下一步的异常运行状态检测提供基础。

3.1 概率功率曲线建模

风速和功率具有随机性和波动性，可将其视为具有相关性的两个随机变量，而Copula函数能够反映两个随机变量之间的相关性[10]。

多元Sklar定理指出，对于边缘分布函数F1(u1)，F2(u2)，…，Fn(un)，存在一个 Copula 函数C满足:

且当F1(u1)，F2(u2)，…，Fn(un)连续时，Copula函数C是唯一确定的，其中F(u1，u2，…，un)是边缘分布函数的联合分布函数。

根据风电机组正常运行数据，计算风速V和输出功率P的累积概率分布，利用能反映风速和功率之间相关性的Copula函数，在不同风速值和置信度下，得到输出功率的条件概率分布对应的上下分位数值，最后在各个风速值下对应的输出功率上下边界值形成的两条曲线就是概率功率曲线[11]。

设V、P分别为风速、功率变量，Fp(p)、Fv(v)分别为其核密度估计累积概率分布函数，C用来描述由唯一Copula函数连接起来的V、P联合分布函数，F是风速累积概率分布取值条件下的功率累积概率分布，即:

其中，V、P分别为工况 B、C、D下的风速、功率变量。

在B、C、D工况下分别选取二元Gumbel Copula函数、二元Frank Copula函数和二元Clayton Copula函数，选用混合Copula函数可得到更加精确的功率曲线上下边界。依次设工况B、C、D的理论等效功率曲线的置信水平1-βi(i=1，2，3)，采用非对称概率区间确定输出功率置信区间上下界，置信区间上下界的分位概率β′ij、β″ij，置信区间不对称系数为κij分别为:

其中，κi-min为第i区域的不对称系数的最小值；κi-max为第i区域的不对称系数的最大值；li为第i区域的不对称系数的变化率；j=1，2，…，m。

分别在工况B、C、D上，利用最大似然估计法分别求出风速整体累积概率分布函数中的参数Fv(v；θ1)和第j段上功率累积概率分布函数中的参数；当测量风速V取值已知时，设条件概率分布F(Fp(p)|Fv(v))的对应分位点分别为p1、p2，即p1、p2分别对应第j段输出功率累积概率分布的取值，分别对p1、p2求逆，得到在该风速条件下，置信等效功率上下边界值，对上下边界求逆即可得到概率功率曲线[12]，如图2中实线所示。

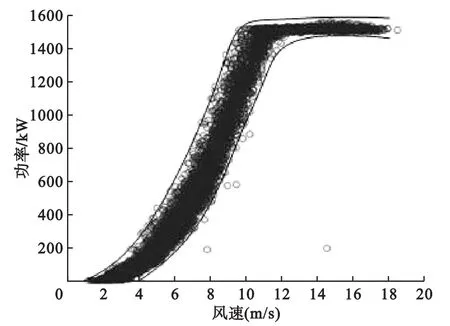
图2 风电机组概率功率曲线

概率功率曲线上下边界外的数据点为可疑点，要确定其为异常点还需要进一步进行验证。

3.2 SVM线性回归模型

SVM线性回归是一种基于统计学习的机器学习方法，在解决非线性、小样本及高维度识别中占有较大优势。 设给定样本为(xi，yi)，i=1，2，…，l，x∈R。xi为第i个输入量，yi为第i个输出量，其基本思想是通过样本集在样本空间找到一个分类超平面，将具有不同特征的样本分开，分类超平面可描述为[13]:

式中，wT为特征空间权系数向量，b为偏置。若样本能够按照各自类别被正确区分，且即对于yi=1，有wT·x+b≥1；对于yi=-1，有wT·x+b≤ -1。

在样本空间中，样本点到超平面的距离为

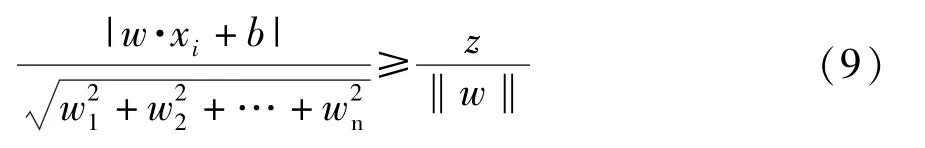
当点到超平面的距离最大时，说明不同特征的数据集之间间隔最远，模型分类效果最好。

4 算例分析

为了验证上述异常数据识别模型的有效性，本文以某风电场风电机组的实际运行数据作为研究对象，机组额定功率为1.5MW，选取10000个连续测量的风速与功率数据对，数据采样间隔为10min。

4.1 Copula函数模型识别

基于Copula函数构建的概率功率曲线如图3所示，在概率功率曲线上下边界外有概率可疑点；相对应的，从图4的B、C、D工况下风速与叶轮转速、发电机转矩、桨距角的时序图中可以看出，在风速未出现较大波动的情况下，叶轮转速与桨距角出现明显波动的数据点。

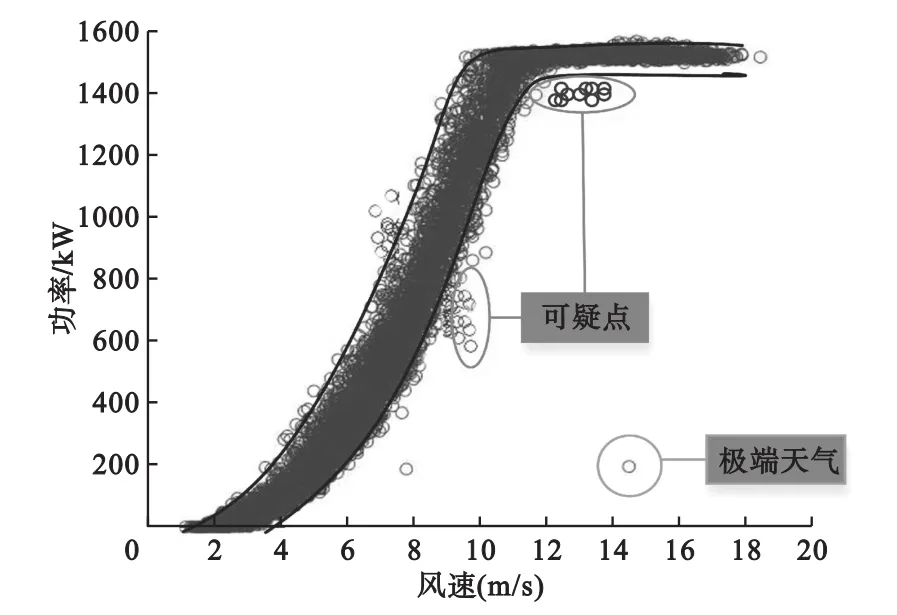
图3 风电机组实测风速功率图

图4 时序图

计算可疑点与相邻正常点之间的欧式距离，并与相邻两个非可疑数据点相比较，结果如表2、3、4所示。由表可知，在工况B恒风速下，叶轮转速低于正常值时，由于转速与转矩的高相关性，转矩也会相应下降，由风速决定的桨距角仍处于正常范围内，但有功功率由于转矩的下降而低于正常值；工况C中欧式空间距离波动范围较小，没有异常数据，与混合Copula函数模型识别结果一致；在工况D恒风速下，桨距角异常时，叶轮转速和转矩均处于正常范围，但有功功率低于正常值。因此可判定概率功率曲线上下边界以外的数据确为异常点。

表2 叶轮转速异常

表3 转矩值正常

表4 桨距角异常

4.2 SVM线性回归模型

本文以残差最小为原则，建立三个工况下相关性最大的特征参量:叶轮转速，转矩，桨距角的SVM线性回归模型，对混合Copula函数模型进行验证，具体过程如下:

(1)数据采集。分别采集风电机组正常运行时三个工况下的叶轮转速、发电机转矩和桨距角数据。采样间隔为10min，每种工况下采样点数为5000个；并随机选取其中前3000个数据作为预测模型的训练样本，余下2000个数据作为测试样本。

(2)建立预测模型。使用均方根误差最小的40组数据集对模型进行多次训练和测试，以RMSE最小为原则，建立精度较高的预测模型。建立模型时，交叉验证选择的原则是RMSE最小，根据训练好的模型，将混合Copula函数模型所识别出的数据及相邻数据点作为测试样本进行检验，图5为测试样本的SVM线性回归模型预测值与实际值对比情况及相应特征变量的残差图，其中残差图控制上限UCL、控制下限LCL之间的距离为3σ。

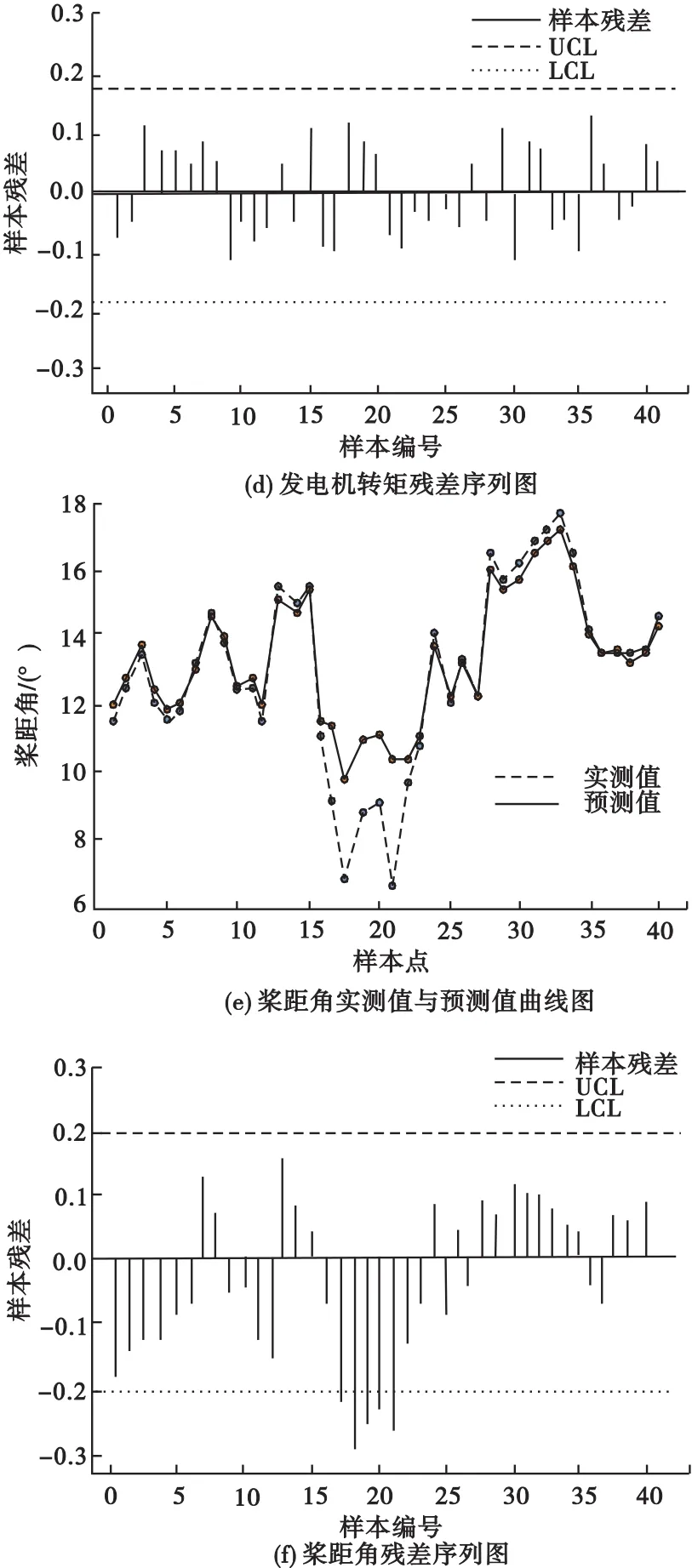
图5 SVM回归模型结果

从图5(a)、(b)中可以看出，工况B中第26个样本点，风电机组的叶轮转速偏离预测值且超出阈值下限，表明该样本点确为异常数据点，此时风轮可能出现轻微故障；从图5(c)、(d)可知，工况C中发电机转矩样本点均在阈值范围内，没有异常数据点；从图5(e)、(f)中可以看出，在工况D第16～21个样本点之间，桨距角偏离预测值且超出阈值下限，表明该样本点为异常点，变桨系统可能出现故障，需要维修人员进行检查。

综上，风电机组各特征参量SVM回归模型结果与混合Copula函数模型所得结果一致，验证了混合Copula函数模型的准确性。

5 结论

本文提出一种基于Copula函数的风电机组异常识别方法，利用风电机组实际运行数据进行仿真分析，得出以下结论:

(1)通过对概率功率曲线上下边界外可疑点的时序分析和欧式距离计算，能够准确判断可疑点是否为异常点。

(2)通过对不同工况下功率曲线影响因素的Kendall秩相关性分析，得到每个工况下影响较大的因素，有利于故障定位。

(3)通过建立SVM线性回归模型，对混合Copula函数模型所确定的异常数据进行检验，结果与混合Copula函数模型所得结果一致，表明混合Copula函数模型能够准确识别异常数据，模型精确性较高。

本文提出的方法基于风电机组历史运行数据，构建等效概率功率曲线并结合数据的时序特性进行分析，能够有效识别异常数据，判断机组故障位置，弥补传统算法的不足，有较强的适应性与实用性，为风电机组异常数据识别提供了一种新方法。