基于R/S分析法的电价预测模型

张仔琪，高志展

(广西大学电气工程学院，广西 南宁 530004)

1 引言

在放松管制的电力市场中，电价具有很强的波动性和随机性，提前准确地预测电价可以使得市场参与者获得更多的收益[1]。对于发电方来说，通过预测市场电价，可以准确把握市场走向，掌握先机，灵活分配合适比例的电能参与市场交易，并在市场中指定最有报价策略以期获取最大的利润。对于用电方来说，成本是影响其收益的关键所在，通过准确预测电价，购电方可以根据自身需求灵活制定合理的用电计划，使其自身的动态成本控制成为可能。准确的电价预测还是市场监管机构对市场进行监管，促使市场健康、稳定、有序的竞争、发展以及各种电价政策的制定的重要依据。可以预见，随着中国电力市场改革的逐步进行，电价预测将越来越受到重视。

电价预测和负荷预测一样，有周期性的特点，但是电力价格表现出来的曲线结构要比负荷的曲线结构更复杂，具体表现为[2]:高频率，多季节性，日历效应，高水平的波动性及不寻常价格波动的比例非常高。即使负荷预测准确，也不能保证利润，规避市场风险。

众多研究表明电力价格具有一定的内在规律，可以通过一定的方法分析电价的历史数据信息，对电价进行相对准确的预测。Mandelbrot首次提出可以利用分形理论中的R/S分析法来分析时间序列，洞察隐藏于混乱无序结构中的相似性、连续性，捕捉结构细节。R/S分析法已被广泛应用在股市预测[3-4]，径流分析[5-6]，降水量预测[7]等不同类型研究领域，并展示出对复杂非线性时间序列进行有效分析的优越性，但是鲜少有将R/S分析法运用于电价预测领域。为此，本文运用R/S分析法探寻电价时间序列的相似性及相似程度，对突变数据进行修正，并采用BP神经网络模型对电价进行预测，取得了很好的预测效果。

2 R/S分析法

R/S分析法又称为重标极差法，该方法通常用来分析时间序列的分形特征和长期记忆过程[10]。R/S分析法由Hurts在1951年研究尼罗河水坝工程时提出，后来由Mandelbrot在1963年将其应用到时间序列的分析中[11]。20世纪90年代通过该方法检验到欧美资本市场的分形结构[12]，证实了证券市场具有长记忆特征和平均循环长度。现在，R/S分析法多运用于分析股票市场。股价和电价具有一定的相似性，影响其波动的因素都较为复杂，因此可以用R/S分析法研究电价序列的相似性及相似程度。

R/S分析法计算步骤如下[13]:将长度为N的时间序列P划分为m个小区间，每个区间长度为n。每个子区间记作Pa，其中a=1，2，3，……，m。Pa中的元素为Ik，其中k=1，2，3，……，n。

这说明可以用最小二乘法对Hurts指数H进行估计。若0.1＜H＜1.0，则它与分形维数D的关系为:D=2-H。H指数大小一般在0～1之间，H的大小可以解释很多非线性动力学特征和演化规律[14-15]。

(1)0＜H＜0.5，说明该时间序列是一个发持续性时间序列，具有频繁逆向转换和不连续倾向。若序列上一个周期向上走，则其再下一个周期多半向下走，H的值越接近0，反向趋势越明显。

(2)H=0.5，说明该序列是一个随机的与时间无光的序列，现在的信息对未来无影响。

(3)0.5＜H＜1，说明该序列具有持续性和循环的倾向，系统存在长期和无周期循环。H越接近1，循环倾向越强。

因为Hurts以上特征，它可以作为在分形理论框架下检验市场有效性的一个重要指标。在R/S分析中，有效市场假说所描述的有效市场特性可以用Hurts指数来代表。H越趋近于1/2，说明电价变动的相关性越小，市场有效性越强，反之，当H越偏离1/2，说明电价变动的相关性越大，市场有效性则越弱。

3 电价预测模型

3.1 输入数据的选择

本文选用广东地区2019年6月份发布的模拟现货交易市场电价数据，选取2019年6月1日至6月15日，共15天360(15*24=360)个数据作为历史数据，以2019年6月1日-15日的电价数据作为样本数据对历史数据进行趋势分析。

如图1所示为15天电价变化曲线。图中可以看出，早间和凌晨时段电价波动较缓，从10:00开始电价出现剧烈波动趋势，不同日期同一时段电价变化趋势存在一定的相似性。

图1 2019年6月1日-2019年6月15日电价变化曲线

3.2 数据预处理

在所获得的广东电力现货市场实时电价的数据中，出现了一些异常突变价格数据，这些价格数据构成了价格序列的毛刺。这些价格毛刺会影响电价的预测，因此对这些数据进行适当的预处理是有必要的。首先对某一时段的实时电价历史数据进行统计，得出一定概率意义下的电价区间，然后将超出该范围的电价部分进行适当比例的压缩。这样既不会改变电价时间序列的大小关系又能去掉突变异常数据对预测的影响。

3.3 BP神经网络

BP神经网络是多层前馈型网络中性能最优越的代表[16]。它模仿人脑神经元对外部激励信号的反应过程，建立多层感知器模型，利用信号正向传播和误差传播反向调节的学习机制通过多次迭代学习，搭建处理非线性信息的智能化网络模型。

BP神经网络模型一般由输入层、隐藏层和输出层组成。BP神经网络的结构如图2所示，其隐藏层可以是一层或者多层，每个层中又包含许多单个神经元[17]。隐藏层虽然不与外界联系，但是其是影响输入输出间关系的关键因素，改变隐藏层的权系数就可以改变整个神经网络的性能。

图2 BP神经网络拓扑结构

BP算法的总体步骤大致如下[18-19]:

4 实例分析

利用matlab软件对R/S分析法和BP神经网络计算过程进行编程，通过R/S分析法对电价变化趋势进行判断，并根据结果采用BP神经网络进行预测。

如图3所示，通过对2019年6月1日～15日广东原始电价数据和修正后点电价数据进行R/S分析，计算得出前360个小时的原始电价和修正后的电价 Hurts分别为0.6327和0.6712。原始数据Hurts值处于0.5～1之间，说明2019年6月1日～15日的电价数据具有一定的持续性，未来电价走势大致和上一时刻呈现相同的变化。在每天的同一时刻，电价变化波动不大。对原始数据进行修正后，由于修正了异常数据，使得数据之间的相关性更大，因此Hurst指数增大由0.6327变为0.6712。

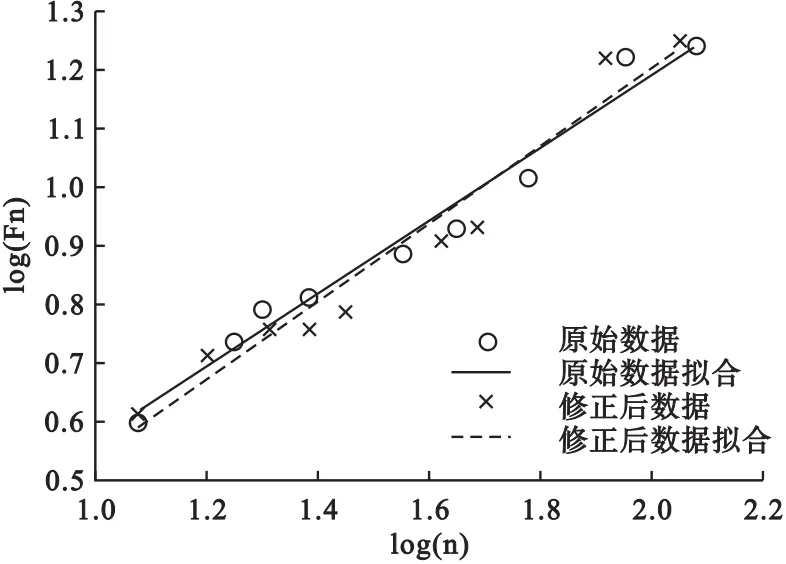
图3 电价变化R/S分析

根据上述分析结果，选用BP神经网络进行预测。分别以2019年6月1日～14日的原始电价数据和修正后电价数据作为训练样本，对2019年6月15日的电价数据进行预测，迭代10次预测结果如图4所示。运用原始数据和修正后的数据预测所用时间分别为0.873s和0.826s，均在1s以内。

图4 预测结果对比

结合图4可以看出，在实时电价预测结果中，经过修正后的数据显示出更好的预测效果。以修正后数据作为训练样本预测的预测结果曲线与实际值曲线更拟合。

在神经网络学习过程中，以修正后的数据作为训练样本，预测误差函数E随着学习轮次的变化情况，如图5所示。迭代24次的时候，该算法已经显示出了很高的精确度，神经网络模型的预测值和实际值相近，误差小于1%。迭代30次后，结果如图6所示，预测值和实际值趋于相同，误差为0.2%，基本可以忽略不计。

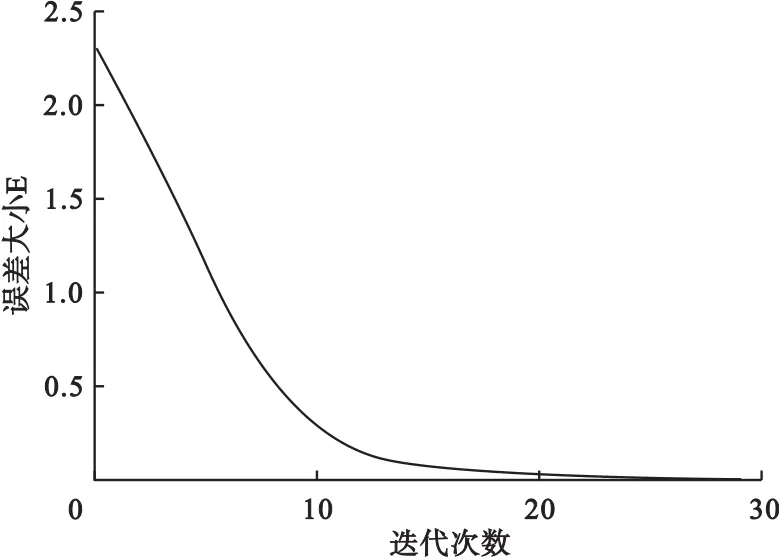
图5 修正后的数据预测误差随迭代次数变化关系图

图6 修正后的数据迭代30次预测结果对比

5 结论

针对电力市场中电价时间序列非平稳随机性特点，通过运用R/S理论对电价变化趋势进行分析，并结合BP神经网络对短期电价进行预测。同时对广东某地区实际电价历史数据进行验证得出以下结论:

运用R/S理论对原始电价数据进行分析，结果表明该地区电价变化具有持续性且存在循环的现象，电价时间序列在时间上存在相似性，分析结果与实际情况相符。对原始电价数据进行修正后，运用R/S分析法验证了修正后的数据比原始数据具有更高的相似性。在算例验证时，BP神经网络预测取得了很好的预测效果，在短时间内就达到了很高的精确度，这说明经过R/S分析修正后使得电价的变化规律更清晰，选取相似性较高的时间序列样本对模型进行训练可以缩短预测时间，提高预测精度。