基于局部离群因子算法的变压器异常检测

曾冬洲，郑宗华

(福州大学电气工程与自动化学院，福建 福州 350108)

1 引言

电力变压器作为电力系统的关键枢纽设备，其工作状态的正常与否直接影响着整个电力系统运行的安全性和可靠性。处于异常状态的变压器，会降低电力系统的供电可靠性甚至造成社会经济损失。因此对变压器的异常工作状态及时识别，并进行状态检修，能够在提高设备可靠性的同时，有效规避检修不足及检修过度等问题[1]。

传统的变压器状态异常检测方法主要包括局部放电检测技术与油中气体分析(Dissolved Gas Analysis，DGA)技术[2-4]。虽然这两种技术在变压器故障诊断方面应用较广，但是也存在一定的弊端。文献[5]中采用局部放电检测技术对疑似异常变压器开展局部放电检测时，需要借助工作经验开展局部放电定位及定量检测工作，不仅耗时耗力，也不能对变压器故障进行及时有效的识别，影响设备运行的可靠性。文献[6]中利用油中气体分析技术对变压器异常状态进行检测，其缺点在于从局部放电的发生到可检测到特征气体往往需要较长的时间，很难捕捉到突发性故障的征迹，实时性比较差。同时，传统的异常检测技术主要使用变压器油分解气体含量、油色谱和红紫外线等数据，未能对变压器在线监测系统中积累的海量电气监测数据进行有效的利用。

针对传统变压器异常检测方法的不足，本文将变压器的电压、电流、功率等在线监测数据作为特征参量，构建一种基于主成分分析和局部离群因子算法的变压器异常实时检测模型，并通过具体算例分析验证该模型对变压器异常检测的有效性和可行性。

2 算法介绍

2.1 局部离群因子算法

2.2 主成分分析

2.3 基于主成分分析的LOF检测算法

针对变压器的电气参量数据存在特征冗余度高和数据量大导致LOF检测算法耗时长的问题，本文提出了一种基于主成分分析的LOF检测算法。首先对原始数据归一化处理，然后利用主成分分析法对数据集高维特征进行降维，减小后期LOF算法的计算量，提高变压器状态异常点的检测效率，最后计算出所有样本点的局部离群因子，将离群因子大于设定阈值δ的样本点归为异常点。具体算法流程图如图1所示。

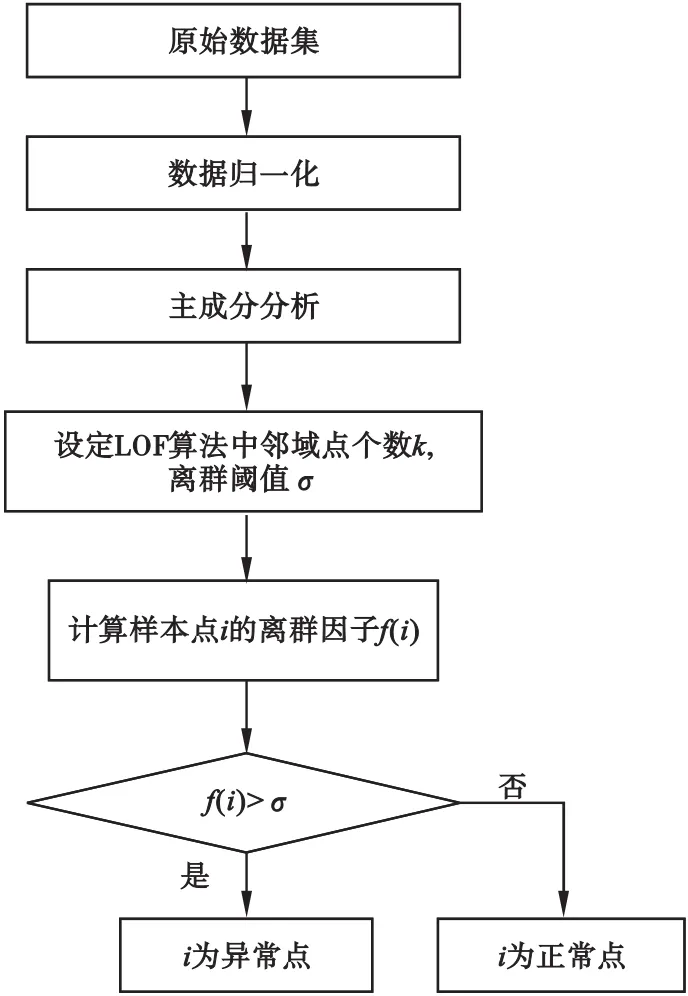
图1 基于主成分分析的LOF检测算法流程图

3 实验数据与环境

3.1 数据描述

本次实验采用的数据来自某变电站一台电压等级为10kV变压器3个月的电气监测数据，数据采样的间隔为15分钟。变压器故障数据集共含8640个有效样本，其中包括102个状态异常点和8538个状态正常点，异常点占比仅为1.18%。变压器监测系统主要监测的电气参量包括任意时刻变压器高压侧的三相电压U1ca、U1ab、U1bc，低压侧的三相电压U2a、U2b、U2c，有功功率Pa、Pb、Pc，无功功率Qa、Qb、Qc，共计12个电气参量。

3.2 数据预处理

本文在实验前对数据的预处理工作主要包括:对含有缺失值的样本采用划分正常和异常的方法通过各自特征属性的均值分别进行填充。另外，为了消除各特征属性间量纲的影响，对所有数据样本采用零均值标准化的归一化方法进行处理，归一化公式如下:

式中，μ和δ分别对应于原始数据的均值和方差。

3.3 实验环境

本实验的软件环境为 Windows10＿64bit，Python 3.5，Jupyter Notebook 5.6.0。硬件环境为Intel(R)6 Core(TM)i3-3240 3.39GHz CPU，8.0GB 内存。

4 实验与分析

4.1 模型评价指标

变压器的异常检测本质上是一个分类问题，即将所有样本分成两类:异常状态类和正常状态类。本次实验采用表1中的混淆矩阵对检测结果分别进行描述，其中TP代表变压器状态实际为异常，检测的结果也是异常的样本数；FP代表变压器状态实际为正常，检测的结果却是异常的样本数；TN代表变压器状态实际为正常，检测的结果也是正常的样本数；FN代表变压器状态实际为异常，检测的结果却是正常的样本数。

表1 混淆矩阵

由于变压器数据集中的异常点占比仅为1.18%，为极不平衡数据集，不能使用传统的准确率指标对检测模型进行有效的评估，因为即使将所有异常点全部误判为正常点，检测的准确率也能达到近99%，这对变压器异常状态的检测将毫无意义。因此本次实验采用灵敏度(sensitivity，SE)和特异度(specificity，SP)的几何均值G作为算法评估的指标，其计算公式如下:

根据式(12)可知，只有当检测结果的灵敏度和特异度都大时，综合指标G值才会大。G值越大，表明算法的检测效果越好。

4.2 实验结果与分析

为了缩减数据集的冗余特征，减少检测算法的计算量，本次实验对数据集的特征进行主成分分析。计算各主成分贡献率及前4个主成分的累积贡献率，各个主成分贡献率情况如图2所示，从图中可以看出，前3个主成分的累积贡献率就可以覆盖原始数据集99%的信息量，因此本文将原始数据集的12个电气参量特征归约至3个主成分特征，可以有效降低后续LOF检测算法的运行时间，提高变压器异常检测的效率。

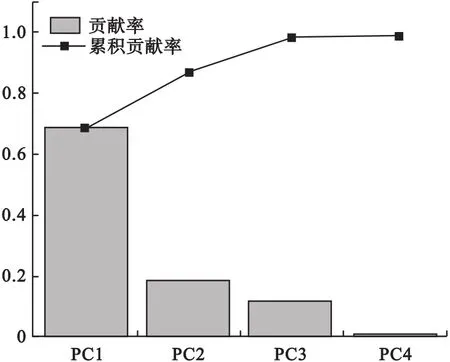
图2 各主成分的贡献率占比分析图

经多次实验测试，LOF算法中离群阈值δ在2.3～2.5之间取值时，检测效果较好，本次实验选定δ为2.4。另外，近邻数k的选择不仅影响到LOF算法检测结果的有效性，且整体算法运行的时间也与k值呈正相关。因此为了获得最优参数k并考量不同k值下有无主成分分析PCA对LOF算法检测效果的影响，实验中分别对不同k值下的LOF算法和基于主成分分析的LOF算法即PCA-LOF进行了测试，两种算法检测结果的几何平均值G如图3所示。

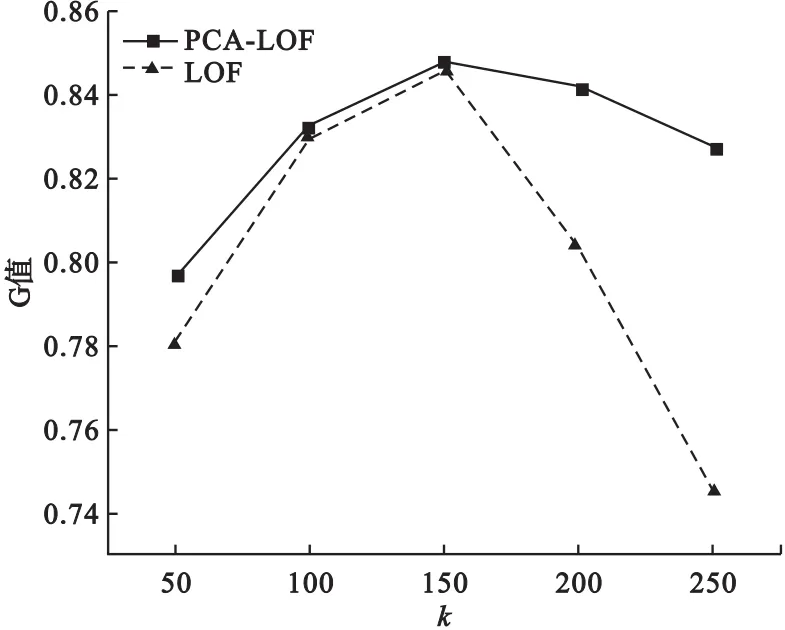
图3 不同k值下LOF与PCA-LOF的几何平均值

分析图3可知，当LOF算法的近邻数k取值在150以下时，主成分分析的数据降维环节对LOF算法的G值影响不大，且当k值取150时，LOF算法和PCA-LOF算法都能获得最佳的检测G值，分别为0.845和0.847。鉴于运行时间的考虑，包含PCA降维处理环节的LOF算法耗时更短，能够在保证检测G值不受影响的条件下提高变压器异常状态的检测效率。

当近邻数k值取最优值150时，PCA-LOF算法在以数据集前两个主成分PC1与PC2为坐标轴的二维平面上的检测结果散点图如图4所示。

由图4可以看出变压器状态异常点基本分布在数据的边缘区域，并且其所处位置的密度相比其他正常点位置的密度更小。

5 结论

本文提出了一种基于主成分分析和局部离群因子算法的变压器异常检测方法，可以实现动态实时数据的异常检测。该方法首先利用主成分分析法对变压器故障数据集进行特征降维处理，然后通过局部离群因子算法计算所有样本点的离群因子，最后将离群因子与设定的阈值进行比较，筛选出代表变压器存在异常状态的离群样本点。实验结果表明，本文算法对变压器的异常状态能进行有效的检测，可以辅助现场工作人员及时发现存在状态异常的变压器，提高变压器运行维护的效率。