Camellia算法S盒的紧凑硬件实现*

魏子豪,张英杰,胡 磊,孙思维,史丹萍,罗宜元

1.中国科学院 信息工程研究所 信息安全国家重点实验室,北京 100093

2.中国科学院大学 密码学院,北京 100049

3.密码科学技术国家重点实验室,北京 100878

4.中国科学院大学 网络空间安全学院,北京 100049

5.惠州学院 计算机科学与工程学院,惠州 516007

1 引言

Camellia分组密码算法由三菱公司和日本电信电话公司在2000年共同设计[1].由于其较高的安全性以及在软、硬件平台上高效的实现性能,该算法在2003年欧洲NESSIE项目中被评选为获胜算法,同年在日本CRYPTREC计划中被评选为推荐算法,2004年成为IETF标准算法,2005年成为ISO/IEC标准算法,2006年成为PKCS#11认证密码.

在硬件平台上实现时,存在这样一种应用场景:由于环境约束,电路芯片的面积必须比较小,因此能使用的电路资源也相对有限,除了满足正常运行功能之外,设计者还需要提供安全加解密能力,例如银行卡芯片、无线传感器节点等.在这种情况下,密码算法实现者对资源面积这一参数更敏感.在Camellia算法中,S盒作为唯一的非线性部件,需要消耗的资源最多,可以优化的空间也比线性部件大,因此通常我们会研究S盒的实现方法.

本文结构如下:第2节简单介绍塔域实现的基础知识和通用方法;第3节将塔域实现和Camellia的具体结构相结合,根据该密码算法的特点采用了针对性的优化方式;第4节汇总了实现方案的数据,并通过仿真实验将它与以前的方案对比;第5节是对全文的总结,以及对未来工作的展望.

2 预备知识

2.1 塔域表现形式

我们可以用其系数组成的向量(b7,b6,···,b0)T来表示b.

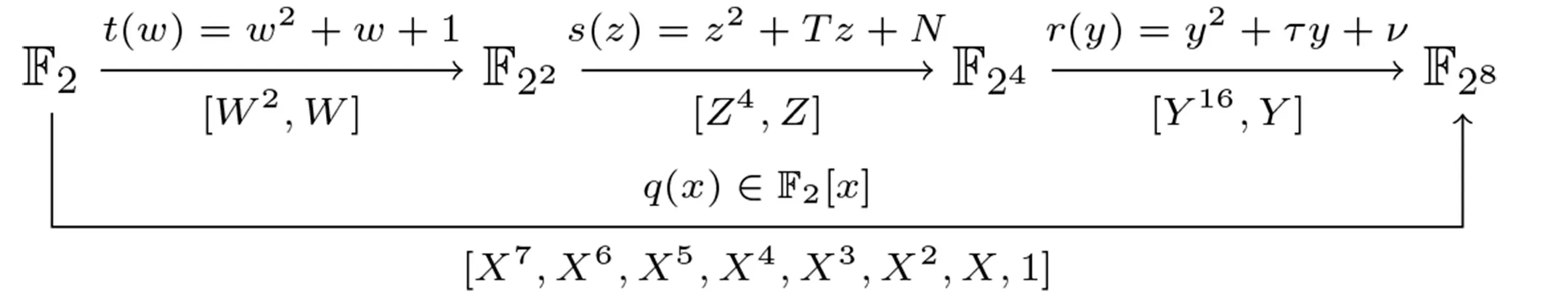
图1 两种不同的域扩张方式Figure 1 Two different ways of field extensions

b=γ1Y16+γ0Y,

γ1=Γ3Z4+Γ2Z,γ0=Γ1Z4+Γ0Z,

Γ3=g7W2+g6W,Γ2=g5W2+g4W,Γ1=g3W2+g2W,Γ0=g1W2+g0W,

其中,γ1,γ0∈F24,Γ3,Γ2,Γ1,Γ0∈F22,g i∈F2,0≤i≤7,即

b=g7W2Z4Y16+g6W Z4Y16+g5W2Z Y16+g4W Z Y16+g3W2Z4Y+g2W Z4Y+g1W2Z Y+g0W Z Y.

我们将这组由W,Z和Y组成的基叫做塔域基,记为T B,

T B=[W2Z4Y16,W Z4Y16,W2Z Y16,W Z Y16,W2Z4Y,W Z4Y,W2Z Y,W Z Y],

在T B下,b可由另一组系数向量(g7,g6,···,g0)T来表示.

由于塔域基中的每个基底分量都是F28中的元素,都可以用多项式基来表示,

T B[i]=W h Z j Y k=(X7,X6,···,X0)V i,i=7,6,···,0,

其中T B[i]表示塔域基的第i个分量,V i表示它在多项式基下的系数列向量,因此塔域基整体也可以用多项式基表示为

b的两组系数向量之间存在如下转换关系

2.2 F28逆运算的塔域实现

γλ=(Γ1Z4+Γ0Z)(Λ1Z4+Λ0Z)

=[Γ1Λ1T+(Γ1+Γ0)(Λ1+Λ0)N T2]Z4+[Γ0Λ0T+(Γ1+Γ0)(Λ1+Λ0)N T2]Z.

ΓΔ=(u1W2+u0W)(v1W2+v0W)

=[u1·v1⊕(u1⊕u0)·(v1⊕v0)]W2+[u0·v0⊕(u1⊕u0)·(v1⊕v0)]W.

2.3 常用电路元件

表1 三种工艺库下常用电路元件的面积Table 1 Area of frequently-used gates in three CMOS technology libraries

3 实现方案

Camellia算法一共使用了4个不同的S盒s1,s2,s3,s4,其中

s2(x)=s1(x)≪1,

s3(x)=s1(x)≫1,

s4(x)=s1(x≪1),

图2 直观地表示了两种基下逆运算之间的联系.

图2 多项式基下求逆和塔域基下求逆之间的关系Figure 2 Relationship between inversion under polynomial basis and inversion under tower basis

进而S(b)可表示为

第2.2节的运算表达式显示,I T B的计算过程受r(y),s(z),t(w)三个不可约多项式影响,参考文献[10]可知,三个多项式共会产生720种有效情况.我们运用文献[6-10]中的知识,对所有有效情况进行了搜索,得到了一种和文献[10]不同,并且效果更好的实现方案,其中多项式的系数和它们的根如表2所示,它们的值均是基于多项式基的表示.

表2 三个不可约多项式的系数及其根Table 2 Values of coefficients and roots of three irreducible polynomials

我们使用5个模块来完成S盒的功能,如图3所示,每个部分的实现细节见下列各小节.

图3 S盒整体结构Figure 3 S-box structure

3.1 头部模块实现方案

头部模块实现了等式(1)中的γ1γ0τ2+(γ1+γ0)2ν部分,记结果为φ.用2.1节的塔域表示符号将γ1γ0τ2和(γ1+γ0)2ν展开到比特级,可得表达式

γ1γ0τ2=(Γ3Z4+Γ2Z)(Γ1Z4+Γ0Z)·(N·Z4+N·Z)2

=g6g2⊕(g7⊕g6)(g3⊕g2)⊕(g7⊕g5)(g3⊕g1)⊕(g7⊕g6⊕g5⊕g4)(g3⊕g2⊕g1⊕g0)]W2Z4+[g7g3⊕g6g2⊕(g6⊕g4)(g2⊕g0)⊕(g7⊕g6⊕g5⊕g4)(g3⊕g2⊕g1⊕g0)]W Z4+[g4g0⊕(g5⊕g4)(g1⊕g0)⊕(g7⊕g5)(g3⊕g1)⊕(g7⊕g6⊕g5⊕g4)(g3⊕g2⊕g1⊕g0)]W2Z+[g5g1⊕g4g0⊕(g6⊕g4)(g2⊕g0)⊕(g7⊕g6⊕g5⊕g4)(g3⊕g2⊕g1⊕g0)]W Z

(γ1+γ0)2ν=[(Γ3+Γ1)Z4+(Γ2+Γ0)Z]2·(N·Z4+0·Z)

=(g7⊕g6⊕g3⊕g2)W2Z4+(g6⊕g2)W Z4+(g7⊕g5⊕g3⊕g1)W2Z+(g7⊕g6⊕g5⊕g4⊕g3⊕g2⊕g1⊕g0)W Z.

设

m9=g7⊕g6m8=g3⊕g2m7=g7⊕g5m6=g3⊕g1

m5=g6⊕g4m4=g2⊕g0m3=g7⊕g6⊕g5⊕g4m2=g3⊕g2⊕g1⊕g0

m1=g5⊕g4m0=g1⊕g0,

则

φ=(g6g2⊕m9m8⊕m7m6⊕m3m2⊕m9⊕m8)W2Z4+(g7g3⊕g6g2⊕m5m4⊕m3m2⊕g6⊕g2)W Z4+(g4g0⊕m1m0⊕m7m6⊕m3m2⊕m7⊕m6)W2Z+(g5g1⊕g4g0⊕m5m4⊕m3m2⊕m3⊕m2)W Z.

运用文献[6-10]中的优化方法,最终表达式为

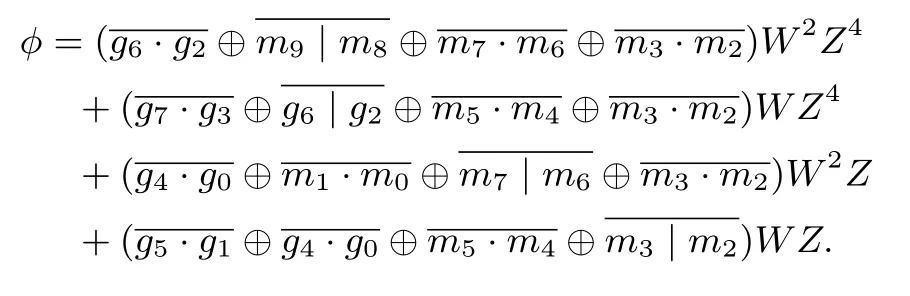
在不考虑m9,m8,···,m0实现方式(即假设比特序列g和m均已知)的情况下,实现该表达式需要8个NAND门、4个NOR门和12个XOR门.

3.2 中部模块实现方案

φ=p3W2Z4+p2W Z4+p1W2Z+p0W Z

λ=(p2p1p0⊕p3p1⊕p2p1⊕p1⊕p0)W2Z4+(p3p1p0⊕p3p1⊕p2p1⊕p2p0⊕p0)W Z4+(p3p2p0⊕p3p1⊕p3p0⊕p3⊕p2)W2Z+(p3p2p1⊕p3p1⊕p3p0⊕p2p0⊕p2)W Z.

传统方法利用了逆运算在塔域上的结构特点来实现,当我们舍弃这一特征,转而应用文献[9]中的方法时,可以得到一个面积更小的实现方案:

t1=NAND(p2,p0)t2=NOR(p3,p1)t3=XNOR(t1,t2)t4=MUX(p3,p0,1)

t5=MUX(p1,p2,1)t6=MUX(p0,t3,p1)t7=MUX(t3,p1,t4)t8=MUX(p2,t3,p3)

t9=MUX(t3,p3,t5),

λ=(t7,t6,t9,t8),

共使用1个NAND门,1个NOR门,1个XNOR门和6个MUX元件.

通过观察可知,

MUX(s,a,1)=s·a⊕s⊕1=NANDN(a,s),

一般情况下,NANDN元件的面积小于MUX元件,当工艺库支持NANDN元件时,我们可以进一步优化t4和t5:

t4=NANDN(p0,p3),t5=NANDN(p2,p1).

3.3 尾部模块实现方案

尾部模块实现了等式(1)中λγ0和λγ1的部分表达式.设

λ=l3W2Z4+l2W Z4+l1W2Z+l0W Z,

k4=l3⊕l2,k3=l3⊕l1,k2=l2⊕l0,k1=l3⊕l2⊕l1⊕l0,k0=l1⊕l0,

e17=NAND(g3,l3)e16=NAND(m8,k4)e15=NAND(g2,l2)e14=NAND(m4,k2)

e13=NAND(m6,k3)e12=NAND(m2,k1)e11=NAND(g1,l1)e10=NAND(m0,k0)

e9=NAND(g0,l0)e8=NAND(g7,l3)e7=NAND(m9,k4)e6=NAND(g6,l2)

e5=NAND(m5,k2)e4=NAND(m7,k3)e3=NAND(m3,k1)e2=NAND(g5,l1)

e1=NAND(m1,k0)e0=NAND(g4,l0),

则

λγ0=(e17⊕e16⊕e14⊕e13)W2Z4+(e15⊕e16⊕e12⊕e13)W Z4+(e11⊕e10⊕e14⊕e13)W2Z+(e9⊕e10⊕e12⊕e13)W Z,

λγ1=(e8⊕e7⊕e5⊕e4)W2Z4+(e6⊕e7⊕e3⊕e4)W Z4+(e2⊕e1⊕e5⊕e4)W2Z+(e0⊕e1⊕e3⊕e4)W Z.

从表达式中可以看到,最后的结果是从18个NAND门的输出中分别抽取4个异或在一起,形成的8个组合.参考文献[7]中的优化方式,在尾部模块中,我们只实现比特序列k和e,将更进一步的异或操作留到之后的模块中去完成.这样尾部模块一共使用了5个XOR门和18个NAND门.

3.4 输入、输出模块实现方案

在有限域中,元素与常数的乘法运算以及元素的2β次幂运算均可转化为对该元素的线性变换,即

其中Mα,Mβ分别表示常数α和2β次幂运算对应的矩阵,因此等式(2)可以重写为

优化方法在求逆运算过程产生的额外效果可以从图4中看出来.

图4 优化方法对逆运算的影响Figure 4 Influence of optimization

进而S(b)可以对应重写为

这个优化只影响输入、输出模块,对其他部分没有影响.

实现输入、输出模块的过程本质上是求解SLP(shortest linear straight-line programs)问题,而SLP问题已经被证明是NP-hard问题[7].目前已经存在多种方法来对其优化,如文献[7-9,16-18],其中文献[17]是将SLP问题转换为SAT问题,利用SAT求解器来运算,对维数较小的矩阵能获得可证明的最优解,而其他文献则都是启发式算法,只能得到较好的结果.针对当前规模较大的输入、输出模块,我们使用了文献[7]中的算法.

α有255种取值,β有8种取值,因此(α,β)共有2040种组合情况.在尝试了所有组合对应的矩阵后,我们发现其中6种组合能使输入、输出模块的实现代价之和最小,其取值和实现代价总和的情况见表3,其中α的值是多项式基下的表达式.而其他组合则会使用更多的XOR/XNOR门电路,通常会增加1-16个.

表3 α、β的最佳取值和矩阵实现情况Table 3 Best values ofαandβ,and sum of implementations of their corresponding matrices

当我们取第一组最佳组合时,输入模块具体为:

一共使用了17个XOR/XNOR门和1个NOT门,实现方案如下:

t1=XOR(b4,b1)t2=XNOR(b4,b2)t3=XNOR(b6,b1)t4=XOR(b7,b0)

t5=XOR(b6,b3t6=XNOR(t4,t5)t7=XOR(t1,t6)t8=XNOR(b0,t7)

t9=XOR(b1,t8)t10=XNOR(t2,t5)t11=XOR(t1,t10)t12=XOR(t4,t10)

t13=XOR(t4,t7)t14=XOR(b5,t13)t15=XOR(t9,t14)t16=XNOR(b6,t15)

t17=XOR(t8,t16),

g=(t1,t6,t11,t2,t9,b1,t14,t3)

m=(t7,t8,t10,t15,t12,NOT(b6),t4,t16,t13,t17).

输出模块具体为:

一共使用了28个XOR/XNOR门,实现方案如下:

t1=XOR(e8,e5)t2=XOR(e6,e0)t3=XOR(e6,e3)t4=XNOR(t1,t3)

t5=XOR(e1,t2)t6=XNOR(e7,t5)t7=XOR(e4,t1)t8=XNOR(t5,t7)

t9=XNOR(e10,t6)t10=XNOR(e9,t4)t11=XOR(e16,t9)t12=XOR(t10,t11)

t13=XNOR(e15,t12)t14=XOR(e17,e11)t15=XOR(e13,e12)t16=XOR(t12,t15)

t17=XOR(e10,e8)t18=XOR(e2,t2)t19=XOR(t17,t18)t20=XNOR(e16,t8)

t21=XOR(t16,t20)t22=XNOR(t8,t11)t23=XNOR(t14,t22)t24=XOR(t14,t16)

t25=XOR(t19,t24)t26=XOR(e14,e13)t27=XOR(e11,t19)t28=XOR(t26,t27),

S(b)=(t28,t8,t23,t25,t6,t13,t4,t21).

4 实验结果

我们将第3节各小节描述的数据汇总到表4中.利用Synopsys Design Compiler软件,结合三种工艺库的库文件,可以对Camellia的各种实现方案做综合仿真,结果见表5.

表4 各模块所用电路元件数量Table 4 Gate number for each module

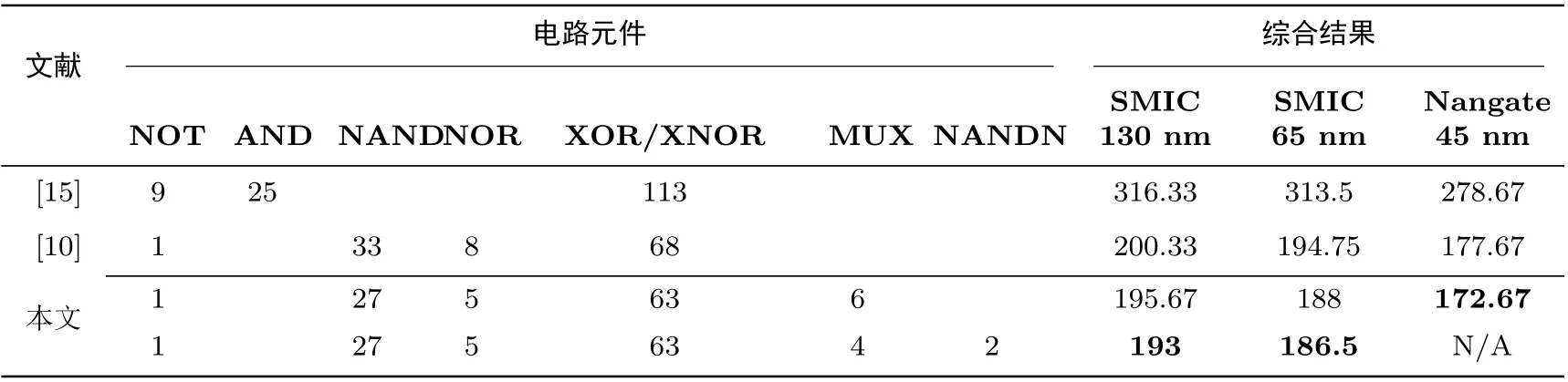
表5 不同论文下的实现方案综合结果Table 5 Synthesis results of different implementations

5 总结

通过划分AES密码算法S盒轻量化实现时的优化方法,我们成功地将这些技术运用到Camellia中,在此基础上当实际使用的工艺库允许一些复合元件时,我们可以做更进一步的优化.实验结果显示,运用了新技术的方案比现有的最佳方案减少了从4.66 GE到8.25 GE不等的面积.

下一步的研究方向是针对深度做优化实现,以及在同时考虑面积和深度两个维度的情况下,设计一种比较平衡的方案.