大跨度钢桁架拱桥施工阶段抗震性能分析

杨方迪

（中铁工程设计咨询集团有限公司，北京100016）

1 引言

为了提升大跨度钢桁架拱桥的抗震能力，以某在建铁路大跨度钢桁架拱桥为研究对象，运用桥梁分析软件Midas Civil 建立该桥的空间结构有限元分析模型，重点分析了结构在纵向、横向以及竖向为主地震作用下的地震响应，计算了大跨度钢桁架拱桥的动力特性，对施工中的桥梁的抗震性能做了综合评价。实验结果显示：扣塔在发生地震时变成了桥梁的危险部件；拱圈合龙能在一定程度上增强桥梁抗震性能；桥梁主体材料在发生地震时产生了超限结构位移。

2 建立模型

本文以某特大桥为研究对象，该桥的具体参数为：主桥为长490 m 的上承式钢桁拱桥，其矢跨比为1/4.495，矢高为109.5 m，该桥按四线设计，线间距均为5 m，拱轴线采用悬链线，拱轴系数为2.0，拱肋内倾角为3.674 5°。采用空间有限元分析软件Midas Civil 可以建立全桥的三维有限元模型。本次研究共采用2 个模型，一个为最大悬臂施工阶段的模型，另一个为主拱合龙施工阶段的模型。采用梁单元模拟拱圈、扣塔以及交界墩，采用拉桁架单元模拟扣锚索。其中，主拱圈主肋采用了Q420q 和Q370q 钢板，而联结系以及拱上立柱则采用Q345q 钢板，桥面主梁使用的是14 跨钢-混结合梁，交界墩采用的是C40 混凝土。采用固结连接的形式来固定交界墩，立柱和主拱的连接方式为刚性连接，阻尼设为0.03。全桥有限元模型如图1 所示。

图1 全桥有限元模型

3 全桥自振特点

使用空间有限元计算软件ANSYS 对全桥进行了特征值分析，并计算出钢桁架拱桥前20 阶频率及周期表数据。由于大跨度钢桁架拱桥具有结构复杂、横竖向刚度相对较弱的特点，在不同的振动频率下，全桥结构所表现出来的振型的主要特征是不同的。在20 阶振型中，有11 阶的振型为结构横向弯曲，3 阶振型结构为竖向振动，6 阶振型结构为墩柱的纵向弯曲[1]。

4 地震激励

在对施工阶段的大跨度钢桁架桥梁的抗震性能进行分析和研究时，大多数情况下会采用时程分析法[1，2]。该特大桥为A类工程，桥址所在地地震烈度等级为Ⅷ度，选用了3 种50 a 发生概率约在2%的罕遇地震波作为输入因子（见图2），设计地震波加速峰值为0.42g，持续时长为40 s。在综合参考各种规范的要求之后，采用了竖直方向地震激励程度为水平方向地震激励程度的65%的方式，分别以纵向地震力、横向地震力以及竖向地震力为主进行了荷载不同组合方式的选取：

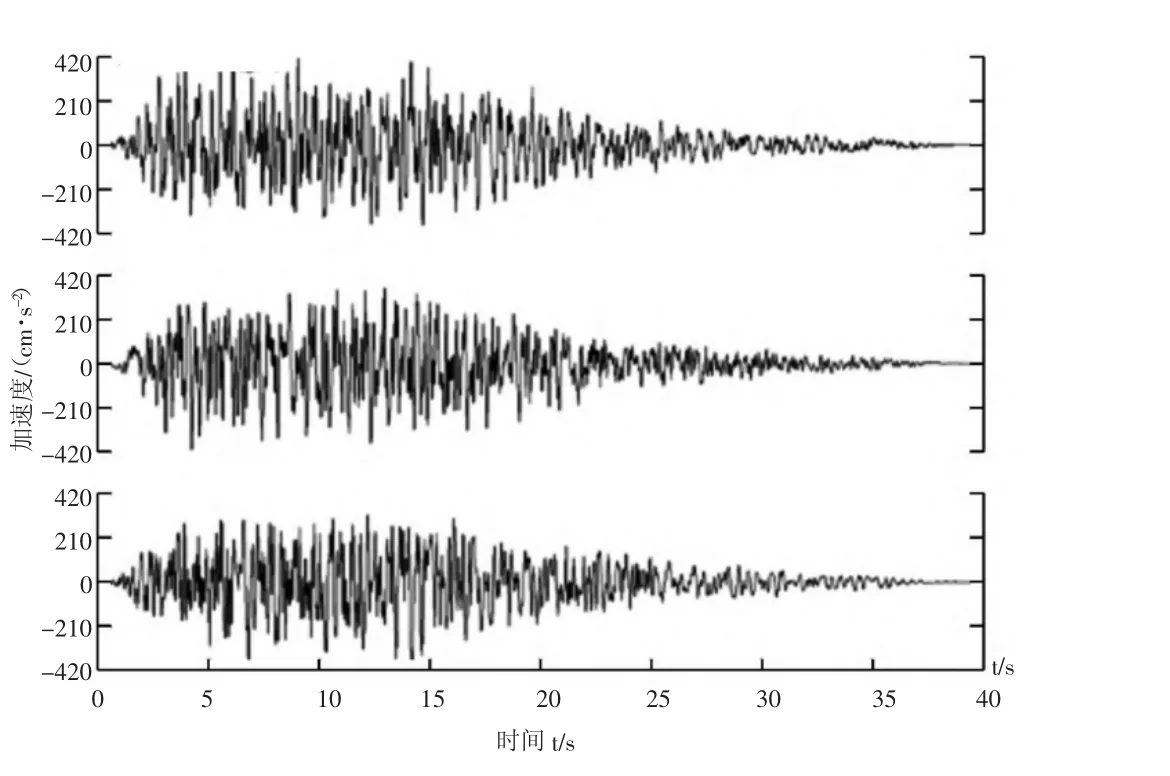
图2 罕遇地震地震波

荷载组合方式1：100%纵向地震力绝对值+30%横向地震力绝对值+30%竖向地震力绝对值

荷载组合方式2：100%横向地震力绝对值+30%纵向地震力绝对值+30%竖向地震力绝对值

荷载组合方式3：100%竖向地震力绝对值+30%纵向地震力绝对值+30%横向地震力绝对值

5 输出结果

5.1 施工阶段桥梁自振特性分析

本文在保证桥梁结构在3 个方向上振型参与度在90%以上的基础上，得出了在桥梁建设过程中悬臂施工阶段以及拱圈合龙阶段前5 阶振型的计算结果，见表1、表2。

表1 悬臂施工阶段结构自振特性

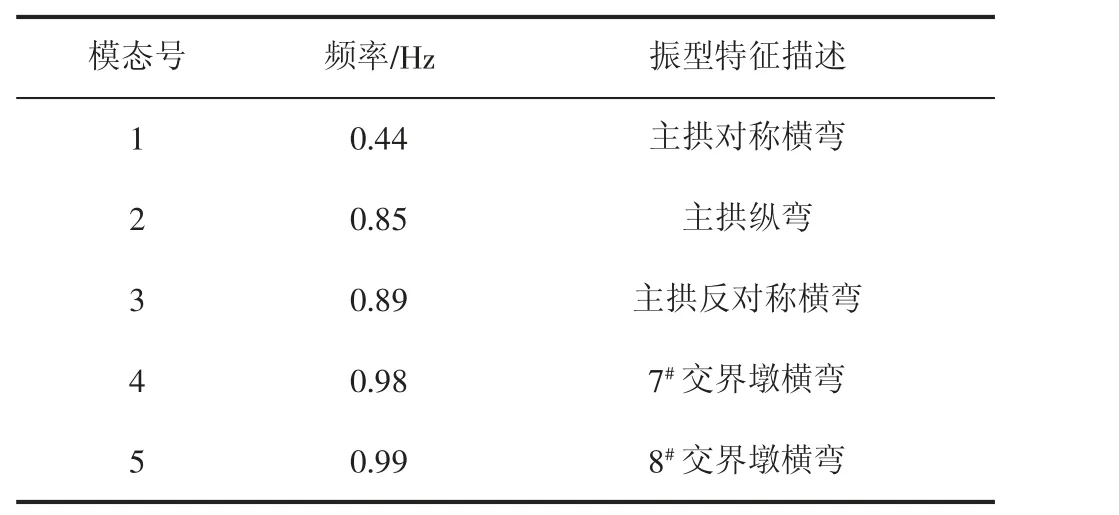
表2 拱圈合龙阶段结构自振特性

计算结果表明，处于最大悬臂阶段时，桥梁结构的前2 阶振型都为结构扭转，其中，扭转和横弯出现的频率最高。在对结构振型特性进行分析、研究后可以得出，在主拱进行合龙之后，结构扭转不会再出现于低阶振型中，反而是横向振动出现的频率最高，这表明主拱合龙对于结构的横向刚度没有显著影响。

5.2 最大悬臂施工阶段地震响应结果分析

桥梁进行最大悬臂施工时。从计算结果可以得出以下结论：

1）上弦杆最大应力为133 MPa，下弦杆最大应力为-128 MPa，扣塔最大应力为145 MPa。3 个位置最大应力均满足材料屈服强度的要求，其中，上弦杆和下弦杆最大拉应力均出现在1/4 跨附近，扣塔最大应力则出现在塔底。

2）在地震作用下，弦杆应力会出现明显的增加，其中，上弦杆的增幅比较明显，尤其是在载荷组合方式1 的作用下，增幅达到了103 MPa。研究还发现，在不同地震载荷作用下，上弦杆、下弦杆以及扣塔应力变化规律基本是相同的[3]。

3）在载荷组合方式1 的作用下，扣塔顶部出现的最大纵向位移为66.4 mm，底部最大纵向位移为165 mm，扣塔顶端和底部出现的最大纵向位移差为131.8 mm。塔墩固结，但桥墩没有固结从而导致墩顶纵向位移大于塔顶位移。在荷载组合方式2 的作用下，扣塔顶部出现的最大横向位移为205.1 mm，底部为192.9 mm。由此可以得出，在地震过程中，扣塔顶端和底端横向位移的变化规律是一样的。

4）交界墩底部在荷载组合方式1 的作用下，其最大拉应力为-6.6 MPa，超过了混凝土极限抗拉强度2.25 MPa。因此，在发生地震时，交界墩出现垮塌的可能性较大。

5.3 主拱合龙施工阶段地震响应结果分析

1）上弦杆出现的最大应力为119 MPa，下弦杆出现的最大应力为-153 MPa，扣塔出现的最大应力为180 MPa，3 处位置均满足材料屈服强度的要求。其中，上弦杆出现最大应力的位置位于1/4 跨处，下弦杆出现最大应力的位置在拱顶处，而扣塔出现最大应力的位置位于塔底处[4]。

2）在地震作用下，弦杆应力会明显地变强，上弦杆的增幅尤为明显，在负载荷组合方式1 的作用下，弦杆最大增幅为85.2 MPa。

3）在载荷组合方式1 的作用下，扣塔顶端所能达到的最大纵向位移为109.2 mm，底部能达到的最大纵向位移为192.3 mm，扣塔顶部和底部的最大纵向位移差为131.8 mm；在荷载组合方式2 的作用下，扣塔顶部所能达到的最大横向位移为205.1 mm，底部所能达到的最大横向位移为192.9 mm。

4）和最大悬臂施工阶段的地震作用相比，在同荷载作用下上弦杆应力有所降低，下弦杆应力升高，这表明，桥梁整体结构受力更加均匀、合理主要得益于主拱合龙对桥梁结构内部的刚度进行了优化，从而其可以更加均匀地承担地震作用力[5]。和最大悬臂阶段地震作用相比，扣塔纵向位移明显减少，这主要得益于主拱合龙后，桥梁结构的纵向刚度有所加强，纵向变形则相应地有所减少，从而降低了地震作用力对扣塔的影响[6]。

6 结论

6.1 合龙能够改善桥梁结构抗扭能力

在进行桥梁悬臂结构施工的过程中，桥梁的扭转刚度以及横向刚度均较低，且在低阶振型下扭转率较高，因此，桥梁结构容易出现扭转变形的情况。在进行主拱合龙施工前，桥梁的横向刚度相对较弱，而合龙完成后则可以在很大程度上增强桥梁结构的抗扭转性能。

6.2 横向缆风锁可增加稳定性

在罕见地震作用下，正在进行最大悬臂施工和主拱圈合龙施工的桥梁，由于其主要构件还未达到要求的屈服强度，扣塔在以横向载荷为主的地震作用下可能会出现较大的位移，因此，可以在施工中增加横向缆风索，以保证桥梁的横向稳定性。

6.3 加强扣塔下部杆件设计

扣塔在以横向载荷为主的地震作用下应力响应与位移响应都比弦杆明显，在以纵向载荷为主的地震作用下，扣塔的应力响应能力较为突出；在以横向载荷为主的地震作用下，扣塔的位移响应能力较为突出。结合实际施工情况，扣锚索索力一般都会比理论索力更大，这样就会出现扣塔恒载异地力增大的可能，在地震载荷作用下扣塔所承受的风险会增加。因此，在实际施工中，可以采取增强扣塔下部杆件设计的措施来保证其稳定性。

6.4 主拱合龙有助于优化桥梁内部刚度分配

实验结果表明，主拱合龙能在很大程度上优化桥梁结构内部材料的刚度，使其在地震作用下受力更加均匀。此外，主拱合龙还能够显著提升桥梁主体结构的纵向抗震性能，从而可以在一定程度上增强扣塔的纵向抗震性能。