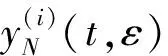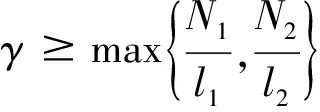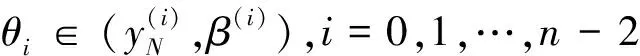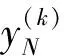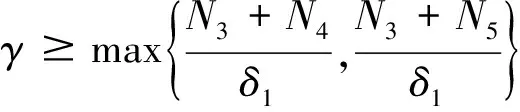一类奇摄动高阶方程非线性多点边值问题
刘 燕,杜冬青
(1.安徽师范大学皖江学院 电子工程系,安徽 芜湖 241000; 2.江苏联合职业技术学院徐州财经分院 基础部,江苏 徐州 221000)
0 引言
源于天体力学的奇异摄动理论已经成为处理非线性问题的重要工具, 近年来, 关于非线性奇摄动边值问题已经得到广泛的研究[1~10]。其中文献[1~3]分别研究了二阶、三阶、四阶非线性微分方程的奇摄动两点边值问题。多点边值问题的存在性结果由Il’in和Moiseev[11,12]发起, 随后, 一些作者讨论了多点边值条件的非线性微分方程的奇摄动问题。如文献[4~5]研究了具有三点边值条件的二阶微分方程的奇摄动问题, 文献[6]讨论了一类具有三点边值条件的三阶微分方程的奇摄动问题,利用Schauder不动点定理、格林函数和上下解法得到边值问题解的存在性和渐近估计,文献[7]采用一种新的Liouville-green变换得到奇摄动二阶微分方程多点边值问题的渐近解,文献[8]利用微分不等式理论和Leray-Schauder度理论,研究了一类三阶微分方程的多点边值条件的奇摄动问题,得到解的存在唯一性和渐近估计结果,文献[9]在文献[8]的基础上将线性多点边值条件推广到非线性多点边值条件,讨论了一类三阶微分方程的非线性多点边值条件的奇摄动问题,并将标量边值问题扩展到向量边值问题[10]。受到以上工作的启发,本文考虑如下一类更为一般的n阶微分方程的附以非线性多点边值条件的奇摄动问题。
εy(n)+f(t,y,y′,…,y(n-1))=0,0 (1) y(i)(0)=gi(y(i)(t1),y(i)(t2),…,y(i)(tm)),i=0,1,…,n-2 (2) y(n-2)(1)=gn-1(y(n-2)(t1),y(n-2)(t2),…,y(n-2)(tm)) (3) 其中0 现作如下假设: [H1]问题(1)~(3)的退化问题 (4) (5) 在t∈[0,1]上有充分光滑的解Y0=Y0(t);[H2]函数f(t,y,y′,…,y(n-1)),关于其变元在相应区域内充分光滑,并存在正常数δ0,δ1使得 fy(n-1)≤-δ0,fy(k)>0(k=0,1,…,n-3), 且 [H3]n-1阶线性微分方程 具有n-1个线性无关的解y1(t),y2(t),…,yn-1(t)∈Cn[0,1],满足 其中 [H4]函数gi(y1,y2,…,ym)(i=0,1,…,n-1)关于其变元在相应区域内充分光滑, 且存在正常数l1,l2使得giyl≥ 0(i=0,1,…,n-1;l=1,2,…,m), 设外部解的形式为 (6) 将(6)式代入(1)和(2)式, 可得退化问题(4)~(5), 以及 (7) (8) 其中Fj-1是有Y0,Y1,…,Yj-1依次确定的函数,Gj-1是依次确定的常数, 由假设[H1][H3]和(7) (8)式可依次确定Yj(t)(j=0,1,2,…) ,得到问题的外部解。 由假设可知, 边值问题(1)~(3)在x=1附近具有边界层项, 引进伸展变量 令 y=Y(t,ε)+εn-2V(ζ,ε) (9) 其中 (10) 且其具有性质 (11) 将(6)(9)(10)式代入(1)(3)式得 (12) (13) (14) (15) 引进光滑函数Ф(t)∈C∞[0,1], 使得 其中p(t)是个多项式函数,σ为足够小的正常数, 令 (16) 由此得到问题(1)~(3)的N阶形式渐近解。 定义1[13]若函数α(t),β(t)∈Cn-1[0,1]∩Cn(0,1)满足 α(n)(t)+f(t,α(t),α′(t),…,α(n-1)(t))≥0,0 α(i)(0)≤gi(α(i)(t1),α(i)(t2),…,α(i)(tm)),i=0,1,…,n-2 α(n-2)(1)≤gn-1(α(n-2)(t1),α(n-2)(t2),…,α(n-2)(tm)) β(n)(t)+f(t,β(t),β′(t),…,β(n-1)(t))≤0,0 β(i)(0)≥gi(β(i)(t1),β(i)(t2),…,β(i)(tm)),i=0,1,…,n-2 β(n-2)(1)≤gn-1(β(n-2)(t1),β(n-2)(t2),…,β(n-2)(tm)) 则称α(t),β(t)分别为边值问题 u(n)+f(t,u,u′…,u(n-1))=0,0 (17) u(i)(0)=gi(u(i)(t1),u(i)(t2),…,u(i)(tm)),i=0,1,…,n-2 (18) u(n-2)(1)=gn-1(u(n-2)(t1),u(n-2)(t2),…,u(n-2)(tm)) (19) 的下解和上解。 定义2[13]设α(t),β(t)∈Cn-1[0,1]满足 α(i)(t)≤β(i)(t),0≤t≤1,i=0,1,…,n-2 函数f(t,x0,…,xn-1)称为关于函数α(t),β(t)满足Nagumo条件, 如果 ξ=maxβ(n-2)(1)-α(n-2)(0),β(n-2)(0)-α(n-2)(1) 存在常数C=C(α,β)且 |f(t,x0,…,xn-1)|≤w(t)φ(|xn-1|) 且 其中, 当p=∞时,(p-1)/p≡1, 引理1[13]若边值问题(17)~(19)满足以下条件 1) 当(t,x0,…,xn-1)∈(0,1)×n时,f(t,x0,…,xn-1)关于变量x0,…,xn-3不减; 2) 当(y1,…,ym) ∈m,gi(y1,…,ym)(i=0,…,n-1)关于每个自变量不减; 3) 存在下解α(t)和上解β(t), 且当t∈[0,1]时, 满足 α(i)(t)≤β(i)(t),i=0,1,…,n-2 4)f(t,x0,…,xn-1)关于α(t),β(t)满足Nagumo条件。 则边值问题(17)~(19)至少存在一个解u(t)满足 α(i)(t)≤u(i)(t)≤β(i)(t),|u(n-1)(t)|≤C,t∈[0,1],i=0,1,…,n-2 定理1 在假设[H1]~[H4]成立下, 则存在充分小的正数ε0, 使得对任意的0<ε<ε0, 边值问题(1)~(3)有解y=y(t,ε)∈Cn[0,1],满足 证明 构造辅助函数 α(t,ε)=yN(t,ε)-γ(1+t)n-2εN+1β(t,ε)=yN(t,ε)+γ(1+t)n-2εN+1 其中γ为待定的充分大的正常数。 显然有 α(i)(t,ε)≤β(i)(t,ε),t∈[0,1],i=0,1,…,n-2 另外, 由微分中值定理, 存在正常数N1,N2,使得 β(i)(0)-gi(β(i)(t1),β(i)(t2),…,β(i)(tm)),i=0,1,…,n-2 =(l1γ-N1)εN+1 以及 β(n-2)(1)-gn-1(β(n-2)(t1),β(n-2)(t2),…,β(n-2)(tm)) =(l2γ-N2)εN+1 β(i)(0)≥gi(β(i)(t1),β(i)(t2),…,β(i)(tm)) β(n-2)(1)≥gn-1(β(n-2)(t1),β(n-2)(t2),…,β(n-2)(tm)) 类似地, 只要γ充分大,就有 α(i)(0)≤gi(α(i)(t1),α(i)(t2),…,α(i)(tm)) α(n-2)(1)≤gn-1(α(n-2)(t1),α(n-2)(t2),…,α(n-2)(tm)) 最后, εβ(n)+f(t,β,β′,…,β(n-1)) 当t∈[0,σ]时, 由外部解的构造知存在正常数N3,使得 =(N3-δ1γ)εN+1 当t∈[1-σ,1]时, 由外部解和右边界层的构造知存在正常数N4,使得 N4εN+1-δ1γεN+1 =(N3+N4-δ1γ)εN+1 当t∈[σ,1-σ]时, 由于每个Vj(ζ)(j=0,1,2,…)具有边界层性态, 故存在正常数N5和充分小的正数ε0,使得 =(N3+N5-δ1γ)εN+1 就有εβ(n)+f(t,β,β′,…,β(n-1))≤0,0 类似可证, 当t∈[0,1]时, 只要γ充分大, 有 εα(n)+f(t,α,α′,…,α(n-1))≥0,0 由引理1可知,对于充分大的γ, 当0<ε<ε0,边值问题(1)~(3)有解y(t,ε)∈Cn[0,1],满足 定理证毕。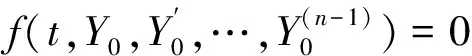
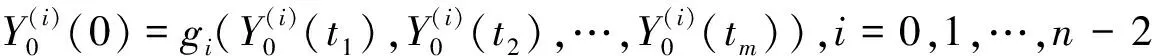
1 问题的外部解
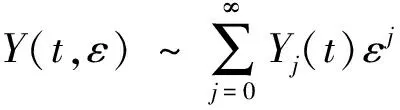
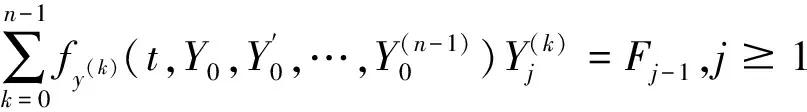
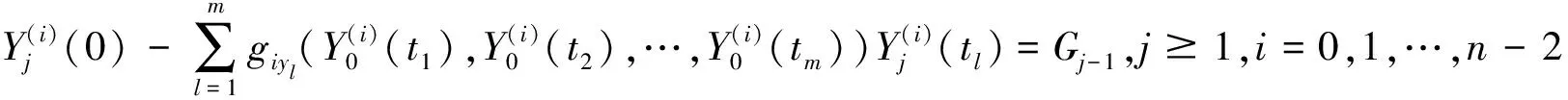
2 边界层校正项
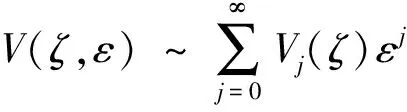
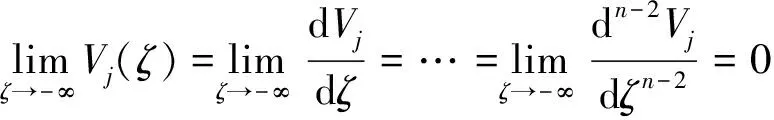


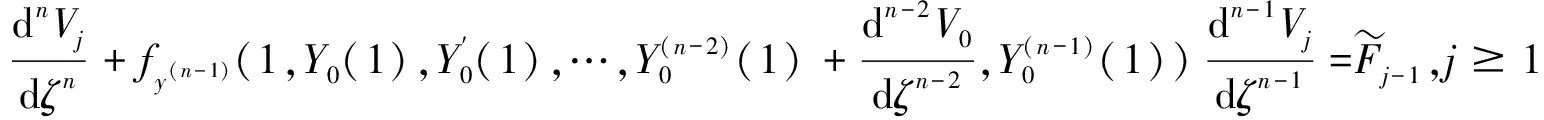
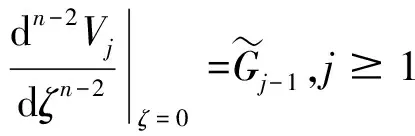
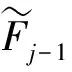
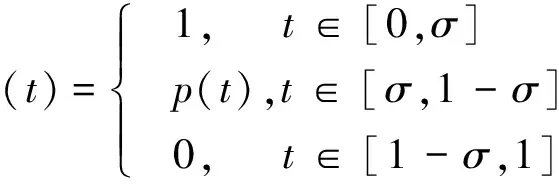
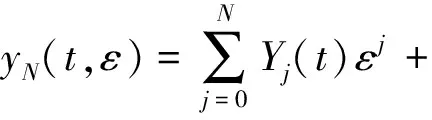
3 主要结果及证明