制动的更精确控制:高速动车组制动系统分级鲁棒控制方法
罗卓军,曹宏发,章 阳,姜岩峰,温熙圆,安志鹏,李邦国
(1 中国铁道科学研究院集团有限公司 机车车辆研究所,北京 100081;2 北京纵横机电科技有限公司,北京 100094)
高速动车组制动系统在控制方面还存在需要提高的地方。一方面,列车级的制动减速度目前还是开环控制,如图1 所示,即使车辆的制动缸压力可通过压力闭环达到精确控制,但是由制动缸压力到产生列车制动减速度还要经过闸片—制动盘摩擦副以及线路工况等环节,闸片摩擦系数[1]和坡道坡度等不确定参数会使列车实际减速度偏离其目标值。因此,有必要通过将列车的电制动力、制动缸压力和速度信息反馈到制动系统,基于自适应控制理论实时估计不确定参数的影响,并计算减速度补偿量,实时修正列车制动力,以提高制动减速度的控制精度,如图1 虚线部分所示。
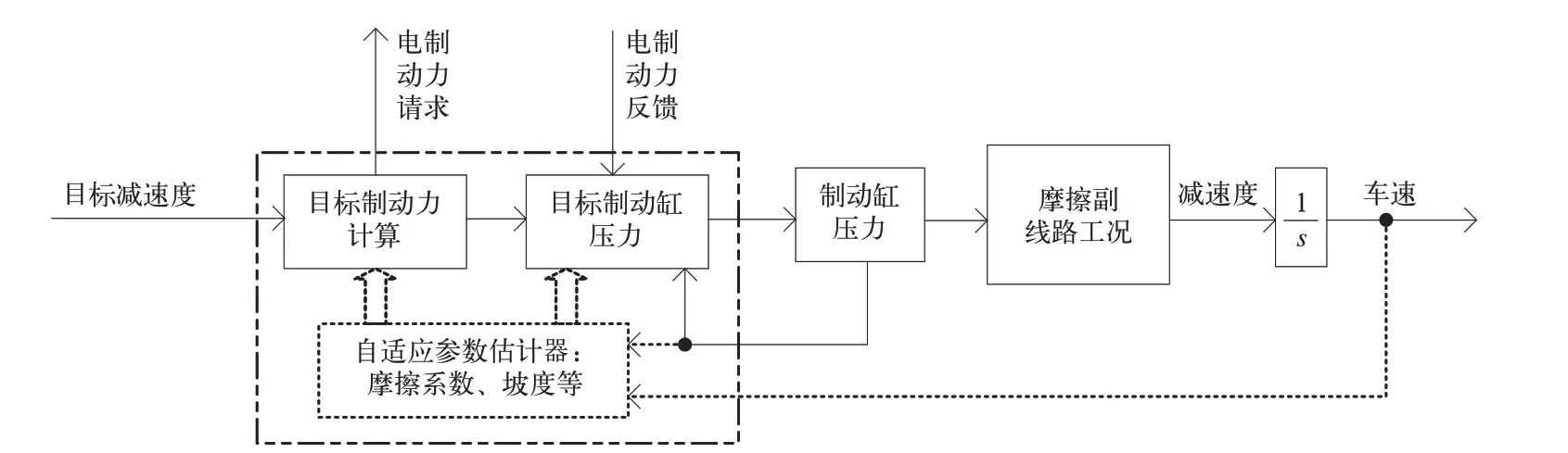
图1 列车级减速度控制示意图
另一方面,车辆级制动控制系统应直接对制动缸压力进行闭环控制。目前,国内部分高速列车的制动系统[1]在进行制动缸压力控制时并非直接控制经中继阀流量放大后的制动缸压力,而只控制中继阀的Cv 先导压力,如图2 所示。若中继阀输出存在误差,即使Cv 先导压力的闭环控制精度再高,中继阀最终输出的制动缸压力仍得不到精确控制。因此,制动控制系统应对采集到的制动缸压力直接进行闭环控制以提高制动缸压力控制精度,如图2 虚线部分所示。

图2 车辆级制动缸压力控制示意图
对于列车级的减速度闭环控制,日本基于PI 控制方法进行过前期研究[2],克诺尔公司称其最新的城轨制动控制系统中已获得应用。而对于车辆级制动缸压力控制方法的研究进展国外则鲜有报道。为进一步提高高速列车的制动控制精度,文中基于自适应控制理论开发了新型列车级减速度闭环控制算法,基于滑模控制方法开发了车辆级制动缸压力鲁棒控制算法,并进行了试验验证。
1 车辆级制动缸压力控制
1.1 控制对象模型
如图2 所示,将中继阀Cv 腔的空气压力和温度分别记为pCv和TCv,则Cv 腔内的空气压力微分方程可记作[3-4]式(1):
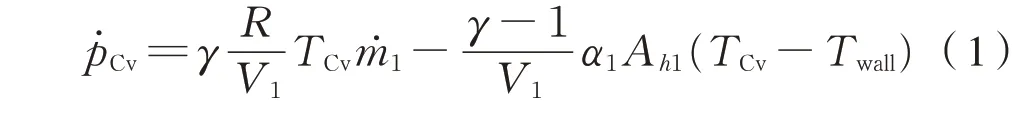
式中:γ为空气比热比;R为空气的气体常数;V1为Cv 腔的容积;ṁ1为充/排气过程中流入/出Cv 腔的空 气 质 量 流 量;α1为Cv 腔 的 传 热 系 数;Ah1为Cv 腔的传热面积;Twall为腔体壁面温度。显然,等式(1)右边第一项表示因充/排气时空气流入/流出引起的压力变化,而第二项表示的是因Cv 腔内空气与腔体壁面传热引起的压力变化。
式(1)中ṁ1为充/排气工况中流经充/排气阀的空气质量流量,若将空气流经电磁阀节流孔的过程以准静态等熵流动过程[5]描述,则该质量流量计算为式(2):

式中:pd为节流孔下游压力(充气时取Cv 腔空气压力pCv,排气时取大气压力patm);pu和Tu分别为节流孔上游压力和温度(充气时取总风压力ps和温度Ts,排 气 时 取Cv 腔 空 气 压 力pCv和 温 度TCv),A1为节 流 孔 的 通 流 截 面 积,而Cq为Perry 气 流 系 数[6],函数g(pd/pu)计算公式为式(3):
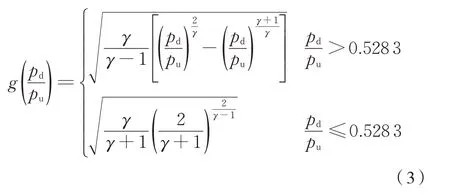
制动系统内用于进行制动缸压力控制的电磁阀为开/关型电磁阀,由开/关型电磁阀的特性可知,当电磁阀气路导通时,通过电磁阀的质量流量可按式(2)计算,但当电磁阀气路截止时,质量流量将骤然降为0,这将导致式(2)中的质量流量不连续。为使控制模型连续,文中在进行压力控制时采用PWM 信号控制,用PWM 周期内的平均质量流量近似代替不连续流量,若将PWM 控制信号的占空比记为u,则式(1)可重新写作式(4):

1.2 滑模控制器
文中基于滑模控制方法[7]开发制动缸压力控制器。首先设计滑模面函数,其原则是当滑模面函数S=0 时,被控系统的状态变量将收敛于其目标值。定义滑模面函数为式(5):



以S作为新的状态变量,对式(5)两边微分可得S的状态方程为式(7):

式中:b̂为用可辨识参数计算出的b的估计值;û称为等效控制,其作用是当系统的不确定参数以其估 计 值 代 替 时û能 使Ṡ=f̂+b̂û-k1(pcr-pc)=0(f̂为f的估计值),因而û可按式(9)计算:

式中,O(ε)为 高阶小量,ks为与b、f的不确定度相关的正增益常数,其推导过程可参考作者前期研究[4,8]。由式(10)可知,当S>0 时有Ṡ为负数,当S<0 时有Ṡ为正数,因此,S可在有限时间内收敛到0。
2 列车级减速度闭环控制
2.1 列车制动的运动学模型
列车制动过程中的运动学模型可表示为:

式 中:v̇为 列 车 运 行 速 度;g为 重 力 加 速 度;θ为 坡道坡度;ω为单位基本阻力和附加阻力(除坡道阻力外)之和;f为整列车的实际闸瓦摩擦系数等效值;Fclamp为列车所有施加气制动的夹钳的夹钳压力之和。
将式(11)两边除M,简化为:
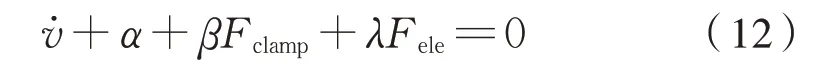
式中:不确定参数α=gsinθ+gω表示列车运行过程中的坡道阻力和基本运行阻力等的影响;β=f/M表示闸片摩擦系数的影响;γ=1/M表示车辆载重变化的影响。在制动系统中对这3 个不确定参数进行实时估计和更新即可较全面地考虑列车制动过程中所受到的不确定参数扰动。
为了避开用微分求列车加速度引入噪声,用一阶滤波器1/(s+γ)(其中s为Laplace 算子,λ为滤波器的转折频率)对式(12)两边进行滤波。该一阶滤波器的单位脉冲响应函数为e-λt,则由卷积定理[9]知滤波后可表示为式(13):

对式(13)左边第一项进行分部积分,则可化为式(14):

式(14)所表示的模型中,除了由不确定参数组成的向量a外,其余各项均能根据制动系统获得的速度、制动缸压力以及电制动力等信息实时计算得到。
2.2 自适应参数估计器
将制动控制系统中对a的估计记作â,将â代入式(14)中可得列车速度的估计值v̂,则速度估计误差为式(15):


t时刻的最优参数估计â(t)应使式(16)取极小值,即∂J/∂â=0,从而有式(17):
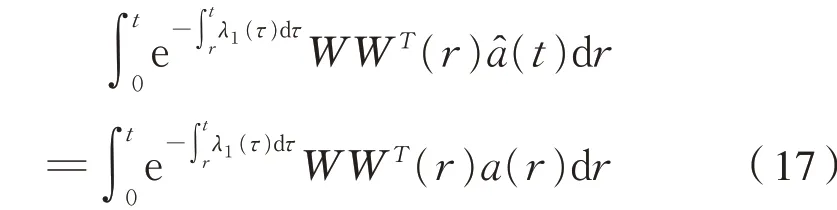
式(17)两边对t求导即可得到用于在线实时更新估计误差向量â的微分方程为式(18):

在制动控制系统中通过数值计算方法同时求解微分方程式(18)和式(20)即可得到不确定参数的估计值,进而用参数估计值计算控制减速度的补偿量,实时修正列车制动力,达到提高减速度控制精度的效果。
3 试验验证
3.1 制动缸压力控制试验
(1)阶跃响应测试
制动缸压力控制过程中PWM 控制信号的周期为300 ms,200 kPa 和400 kPa 阶跃测试的压力响应曲线如图3 所示,从图中可见,电磁阀只需动作2~3 次即可将制动缸压力从0 调至目标值,制动缸压力的控制精度可达到±8 kPa;另外,200 kPa阶跃测试的90% 制动缸压力上升时间为1.65 s,400 kPa 阶跃测试为1.95 s。

图3 制动缸压力控制阶跃响应测试
(2)故障模拟测试
模拟中继阀少输出10% 的制动缸压力(将采集到的制动缸压力乘0.9),对比只对Cv 腔压力进行闭环控制和文中直接对制动缸压力进行闭环控制2 种控制方法的控制效果,故障模拟测试如图4所示。图4(a)所示为只对Cv 压力进行闭环控制的效果,由于中继阀输出故障,导致制动缸压力大概有10%(约30 kPa)的控制误差;而图4(b)所示为文中直接对中继阀输出的制动缸压力进行闭环控制的控制效果,控制器通过提高Cv 压力以使得制动缸压力达到目标值,且90%压力上升响应时间基本与正常工况相同(约为2 s)。

图4 故障模拟测试
3.2 列车减速度闭环控制验证
目前高速动车组上使用的开环控制模式的控制效果如图5 所示,工况为紧急制动EB,制动初速为250 km/h,从图看出,受制动不确定参数(主要为闸片摩擦系数、坡度)的影响,列车实际减速度存在较大的控制误差。
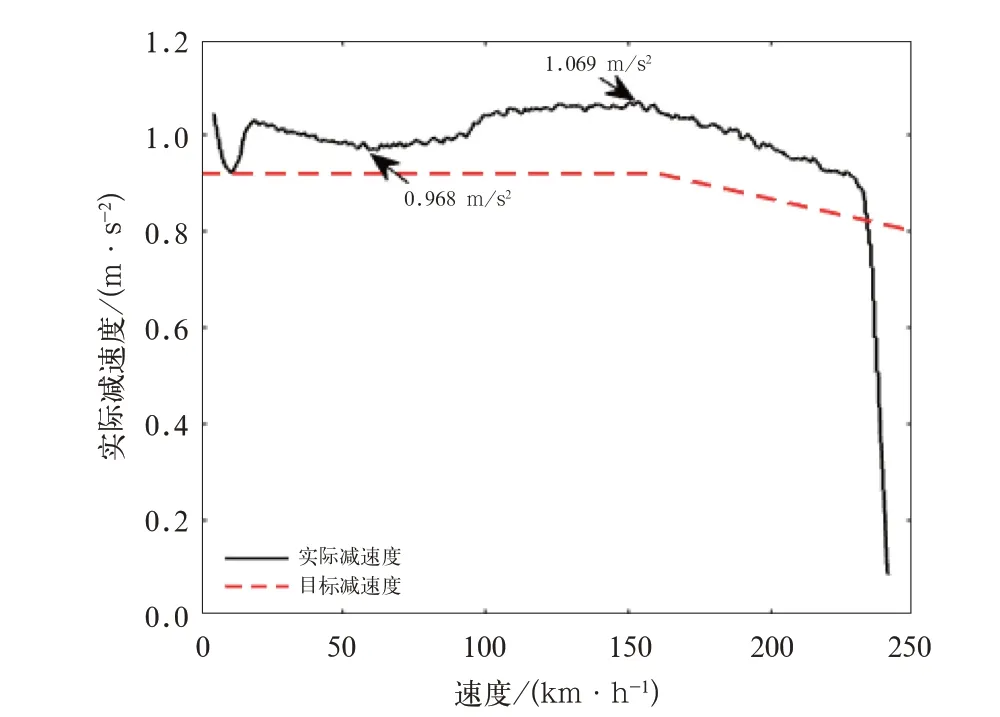
图5 闭环控制的实际减速度与目标减速度曲线
减速度闭环控制算法根据所估计的制动不确定参数计算出的控制减速度补偿量如图6 所示,补偿量为负值表明当前实际减速度大于目标减速度,需要将实际减速度降低以匹配目标值。

图6 减速度闭环控制算法计算出的减速度补偿量
由于一些非技术原因,减速度补偿量并未用于控车,但可将图5 中的实际减速度曲线与图6 中的减速度补偿量相加,即可得到若补偿量用于控车时列车减速度的闭环控制效果,如图7 所示,若减速度闭环控制算法用于控车,列车的实际减速度将能较好地贴近目标减速度。

图7 减速度闭环控制的理论控制效果
4 结 论
文中针对高速列车制动控制在列车级和车辆级2 方面存在的不足,在车辆级基于滑模控制方法开发了制动缸压力滑模控制器,在列车级基于自适应控制理论开发了新型的减速度闭环控制算法。
所开发的车辆级制动缸压力滑模控制器直接以中继阀输出的制动缸压力为闭环控制对象,即使在中继阀存在10%左右的输出误差的情况下仍能快速将制动缸压力控制到目标值,控制精度可达±8 kPa,控制过程中无超调。
所提出的列车级减速度闭环控制算法可根据列车速度、制动缸压力和电制动力实时估计列车制动不确定参数,计算列车制动减速度补偿量,该减速度补偿量可用于修正列车制动力,使列车实际减速度收敛于目标减速度。

