水介质下轮轨制动黏着试验研究*
吴萌岭,周嘉俊,马天和,刘寅虎
(1 同济大学 铁道与城市轨道交通研究院,上海 201804;2 南京浦镇海泰制动设备有限公司,南京 211800)
黏着机理的研究是轨道车辆轮轨关系的核心问题。轮轨间的黏着现象是列车牵引、制动作用发生的基础,铁道车辆的制动尤其离不开轮轨的黏着。列车制动时黏着力不足会引起车轮滑行,造成车轮擦伤,导致停车距离超限,严重影响轨道车辆的运营安全。
轮轨间的黏着系数与许多因素有关,影响黏着系数的主要因素是接触表面的几何形状、轴重、环境温度、轮轨之间的相对滚动滑动速度、摩擦接触振动等,但是实际应用中,最关键的因素是轮轨表面状态。当在有水、油、树叶等“第三介质”污染的轨面条件下,轮轨间黏着系数将大大降低。
对于轮轨间黏着的研究,一般认为,黏着系数与滑移率、速度关系较大,每种速度和滑移率都对应某个黏着系数值,如图1 所示。但是,目前对于黏着系数值的大小及影响因素,尚无统一的定论。

图1 黏着系数—滑移率—速度曲线
1 轮轨黏着
1.1 黏着系数定义
通常把轮轨之间的最大切向作用力叫做黏着力,把黏着力与钢轨对车轮的法向反力之比叫做黏着系数。黏着系数是表示车辆与钢轨间黏着状态的指标,它表示了车辆的牵引力或制动力传递给钢轨的可能程度,具体地说就是车轮圆周方向的切向力与车轮垂直载荷之比的最大值[1]。
目前除了黏着系数这个名称以外,还有假定黏着系数、要求黏着系数、计算黏着系数、有效黏着系数、实际黏着系数、可用黏着系数、利用黏着系数、牵引和制动黏着系数[2]。
1.2 轮轨间黏着特性
轮轨间的黏着特性可以用黏着系数—滑移率曲线来描述。早在19 世纪,Hertz 发表了《论弹性固体的接触》,基于Hertz 的理论,可以对轮轨接触的法向力进行计算。在干燥轨面的条件下,英国学者CARTER 于上世纪20 年代,利用解析法求解了二维弹性体滚动接触问题,并划分出接触斑中黏着区和滑动区,得出了轮轨间切向力和蠕滑率之间的关系[3]。所得的黏着系数—滑移率关系如图2(a)所示。后来在此基础上,又发展出了JOHNSON K L 的三维无自旋弹性球滚动接触理论[4]、VERMEULEN P J 和JOHNSON K L 的 椭 圆接 触 理 论[5]、沈 志 云 的 沈 氏 理 论[6]、KALKER[7-8]简化理论和精确理论、POLACH[9]的快速解法等。虽然Kalker 的轮轨蠕滑理论在铁路中得到了广泛的应用,但是速度对黏着系数的影响在Kalker 的理论并未考虑。然而,试验结果却表明速度对黏着系数的影响是显著的。随着滑移率的增大,轮轨间切向力首先会不断增大到一饱和值,随后便会开始下降,如图2(b)所示。为了考虑速度的影响,各国学者从许多方面做出了不懈努力。ORE[10]、OHYAMA T[11]、KALKER[12]等尝试在KALKER 理论中在滑动区采用动摩擦系数,在黏着区应用静摩擦系数。我国的陈厚嫦还尝试在Kalker 理论基础上考虑函数型摩擦系数[13],对简化理论和精确理论进行了修改。
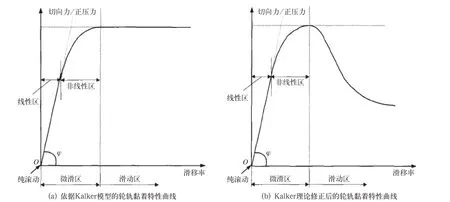
图2 黏着系数—滑移率特性曲线
虽然基于弹性力学黏着特性的理论研究已经有了长足的进展,但是对于实际黏着系数饱和点的大小及所对应的滑移率,目前还是没有定论。
在制动工况下,黏着系数决定了可施加的制动力的大小。当制动力大于黏着力时,轮对会出现滑行现象,车轮的运行状态将从微滑区过渡到滑动区。目前的绝大多数轮轨滚动接触的研究,研究领域都局限于微滑区。但是制动滑行工况,车轮的黏着状态涉及到微滑区和滑动区之间的过渡。对于滑动区、微滑到滑动的过渡过程的黏着研究,目前无论是理论还是试验都存在不足,尤其是由“第三介质”引发的低黏着工况。目前对于有水、油、树叶等“第三介质”污染的低黏着工况,试验测试是最好的研究途径。
2 水介质工况下黏着试验研究
以最常见的水介质为“第三介质”,探究水介质工况下的制动黏着特性,利用1∶1 滚动试验台进行黏着系数的测量试验。为取得较为完整的黏着系数—滑移率曲线,试验中将滑移率范围尽量扩大。
2.1 试验条件
制动系统综合试验台为1∶1 全尺寸滚动试验台,利用带有60 轨轨头形状,1.25 m 直径的轨道轮来模拟无限长的平直轨道。列车使用假车体和CRH380A 拖车转向架进行模拟,如下图3 所示。试验台由最右侧的两个牵引电机提供动力,驱使轨道轮旋转,带动转向架上面的轮对旋转。试验台最左侧为4 个飞轮组,用以模拟列车的惯量。飞轮组左侧为同步齿轮箱,保证带有轨道轮的两根轴转速一致。假车体被与地面固连的反力架所固定,假车体上可以加载不同重量的砝码以模拟不同的轴重。
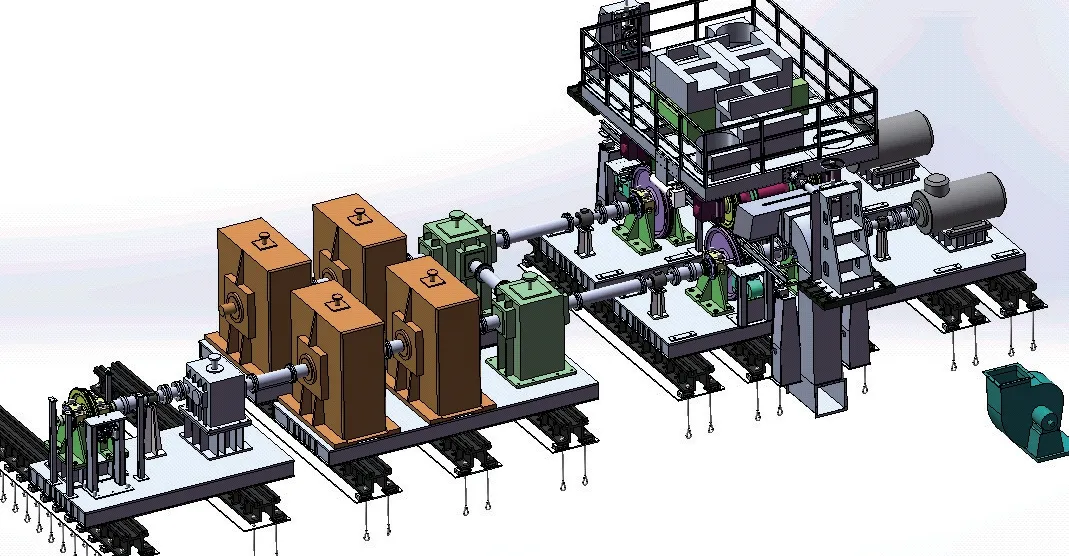
图3 制动综合系统试验台示意图
试验中采用水泵及喷嘴向试验台轨道轮与车轮接触处喷水,如图4 所示。喷水的水量为每个接触面500 mL/min,由于水介质的存在,每次试验开始前,均需要让轮轨接触区充分润滑,再进行制动。

图4 喷头位置示意图
2.2 试验流程
试验在水润滑的工况下进行,为探究制动工况下的黏着特性,轮轨间的滑移率尽量要设置地较大。试验选取3 种轴重等级、6 种速度等级,滑移率预设值为25%。试验流程如下:
(1)使用牵引电机将轨道轮与车轮牵引至一定速度。
(2)牵引至目标速度后稳定后,将电机控制模式切换为转矩控制模式,以维持轨道轮在制动过程中保持恒定速度。
(3)开启水泵对轮轨接触点洒水。
(4)对EBCU(电子制动控制单元)预设防滑排气滑移率极限值。
(5)开始对转向架上一根轴施加制动,实时采集转向架轴速、轨道轮速、扭矩仪力矩等参数。
(6)当滑移率达到预设值时EBCU 控制制动缸一次排空。
(7)重复试验。
(8)改变试验速度,重复1~7 步,直到全部速度工况试验完毕。
(9)改变轴重,重复1~8 步,直到全部轴重试验完毕。
试验过程中洒水一直进行,通过采集记录轮对受到的正压力和切向力,轨道轮与制动轮对的速度,实时计算出当前时刻下的黏着系数—滑移率曲线。
2.3 试验结果
进行了3 种轴重等级、6 种速度等级的黏着测试试验,轴重与速度的序号根据数值由小到大排列。每组包含5 次重复试验。通过5 组重复工况,拟合出当前工况下的黏着系数—滑移率曲线。数据截取制动开始指令和防滑阀排气指令之间的数据,试验结果重复性较好。其中轴重等级1、速度等级1~6 及速度等级1、轴重等级1~3 的试验结果如图5 所示。随着滑移率的增大,切向力与正压力的比值先是增大到某一饱和值,该饱和值对应的滑移率大约为1%左右。随后在滑移率大约1%~5%的区段上,切向力与正压力的比值随着滑移率的增大而减小。但是如果滑移率进一步增大,切向力与正压力的比值将会出现一种上升的趋势,且能够上升到的数值远大于饱和值点的数值。
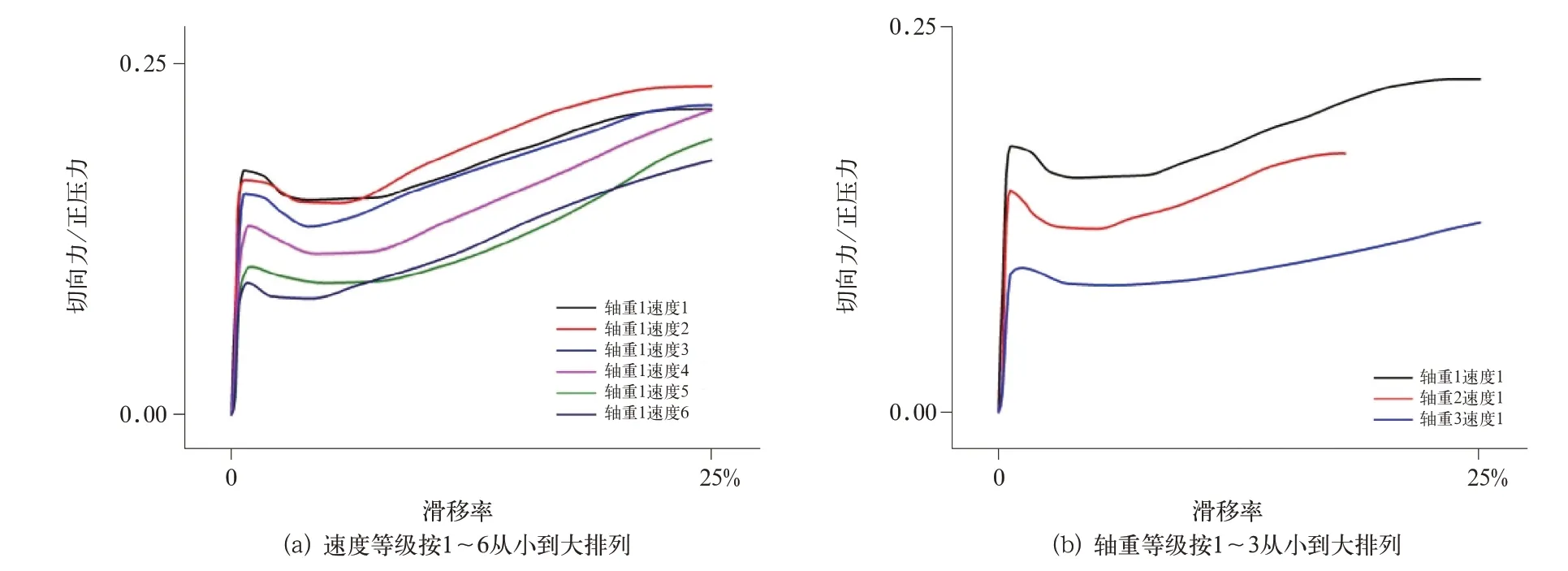
图5 黏着系数—滑移率曲线
从图中5 可以看出,在0~5%滑移率范围内,切向力与正压力的比值随着滑移率是先上升到某一饱和值点后下降的。随着速度的增大,相同轴重下的饱和值点逐渐下降;相同速度条件下,饱和值点随着轴重的增大而下降。这些0~5%滑移率范围内的试验结果,从趋势上和经典轮轨滚动接触理论是符合的。0~5%滑移率范围内,全部工况的饱和值点与速度及轴重的关系如下图6 所示。
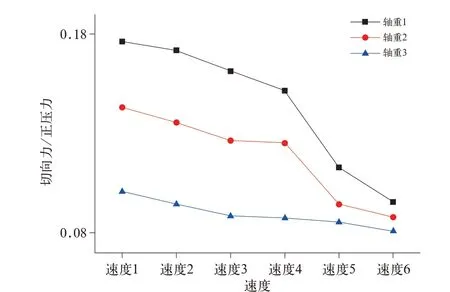
图6 1%滑移率对应的饱和值与速度、轴重关系
但是如果进一步增大滑移率,切向力与正压力的比值不像传统理论所描述的一直下降,反而有所上升,到达25%滑移率时该比值是1%对应饱和点该比值的1.2~1.6 倍,这是基于弹性力学的轮轨滚动接触理论所无法解释的。目前对于水介质工况下,5%~25% 滑移率之间出现切向力与正压力比值上升的原因,尚未知晓。作者推测是由于轮轨间的大滑移作用产生了剧烈摩擦,极高的摩擦热导致轮轨接触区域内水膜破裂,从而导致该现象的出现。
3 结 论
(1)利用1∶1 滚动试验台进行水介质下的制动黏着系数测量试验,试验结果证明在滑移率0~5%范围内,切向力与正压力的比值随着滑移率先上升后下降。在大约1%滑移率处对应着切向力与正压力比值的饱和值点。随着速度的增大,相同轴重下的饱和值点逐渐下降;相同速度条件下,该饱和值点随着轴重的增大而下降。
(2)随滑移率的增大切向力与正压力的比值上升到一定的饱和值后,随后略有下降,当超过5%滑移率后,该比值又有上升的趋势。

