影像与图形融合的视觉信息可视化传达仿真

栾黎荔

(湖北工业大学工程技术学院，湖北 武汉 430068)

1 引言

视觉信息可视化是图像处理中的一个重要内容，将信息转化为可视化的阶段是一个尤为复杂的设计过程。信息可视化可以在多方面促进人们了解和掌握多种复杂数据或图像，采用高效的视觉表达手段，使用户完成对数据的读取和识别，进一步实现用户对所期望有效信息的获取，然而在获取信息的过程中，通过可视化的方式，可以很大程度上减轻海量信息给用户造成的压力。

影像与图形是两种不同形态的个体，会展现出与众不同的视觉感受。将两者融合后可以呈现出崭新的感官效果。在信息交互的传达时代，影像与图形的融合能够作为传达信息的重要载体，是具备某种特定信息的视觉形象。图形是对现实事物简化形态，是人为创造，是虚假的，不仅能够表达真实世界中存在的事物，对于其它不存在的事物也能够抽象的进行视觉化表达。但在视觉信息可视化传达过程中很容易出现图像过于复杂和效率较低等问题。

朱立霞等人[1]提出一种基于时间序列的螺旋图可视化方法，即可以将多个阶段的数据同时展示在一个平面空间内，还能够在有限的空间内展示任意时长的数据。首先将状态圆环上的数据点进行分类，然后在相邻的状态圆环之间设置虚拟绑定圆环，通过边绑定的函数将状态圆环上的数据点映射到其对应的虚拟绑定圆环上。最后在状态圆环与其对应的虚拟绑定圆环之间绘制Bézier曲线，在虚拟绑定圆环与虚拟绑定圆环之间绘制螺旋线，从而实现边绑定的效果。仿真结果表明：该方法能够有效地对大规模数据进行可视化，并能有效地缓解视觉杂乱的问题。

孟令愚等人[2]提出一种基于电网信息三维可视化系统数据管理。首先通过MongoDB技术、B/S技术，通过数据读取和改写使其具有伸缩性能，能够实时处理数据。然后建立三维可视化平台，能够从多方面提高资源搜索效率与空间的规划管理。在三维可视化过程中，要重点关注设备管理三维化，一方面要提升设备上下架效率；另一方面要增加故障告警管理可视化程度，同时注重其机柜使用效率统计可视化。实验结果表明：该方法能够提升数据集成的性能，使数据达到可视化传达。

上述两种方法容易产生图像失真率较高，对比度较低的现象，很难体现出图像的具体结构特征，图像可视化传达效果较差。本文所提方法将影像与图形融合进行融和，能够合理处理画面扭曲的现象。采用映射处理方式，将三维信息转换成平行光模式下的成像效果，所得图像质量更高，能够体现出细节特征，从而实现视觉信息可视化。

2 影像与图形融合

影像与图形这两个元素独立且兼容，两者融合在一起，能够给人们展现出一场与众不同的视觉盛宴。被普遍应用于广告宣传片和海报当中，来增加宣传内容的视觉效果，并且十分吸引观看者的眼球，增加视觉冲击效果。

通过融合不同来源的影像数据，并将其充分利用，这两个元素同时出现在一副画面中，并且都保留了各自的主要特点，在视觉上或者意象上具有关联性[3]。综合考虑影像与图形两者在融合时所耗费的时间与成本，故运用IHS变换方法与Brovery融合方法相结合的方式进一步完成融合。

2.1 IHS变换与Brovery融合

IHS变换方式主要是通过多光谱影像的变换来实现的。首先获取到I、H、S这其中的分量，然后根据黑白影像反复变换对多光谱影像I分量实施处理，通过黑白锐化的形式来突出融合后的图像分辨率。能够在一定程度上保存住其中的具体细节特征。

在为解决IHS进行变换时较为费时且效率较低的问题[4]，提出一种快速IHS变换方法，其表达式为

(1)

其中，δ=P-I，I=(R0+G0+B0)/3，P代表黑白影像的灰度值，R0、G0以及B0代表色彩影像的不同波段，Rnew、Gnew以及Bnew代表完成融合后的图像。

通过均值标准差实施归一化处理[5]，得出表达式即

(2)

其中，P′代表配准结束后的高分辨率黑白影像，P代表未配准时的高分辨率黑白影像，μHRP代表未配准时的影像均值，σHRP代表未配准时的方差，σLRI代表未配准时较低分辨率的I均值，μLRI代表未配准时低分辨率的I分量方差。

Brovery融合完成后的影像方式主要根据较高分辨率的色彩影像和多光谱影像共有的波普区间为基础[6]，其表达式为

(3)

式中，R0、G0以及B0所描述的是色彩影像的不同波段，P所描述的是黑白影像。

2.2 两者相结合的融合方法

针对多光谱影像与黑白影像融合后会出现光谱特性扭曲严重的现象。δ能够决定在融合完成后影像的光谱扭曲程度，若P和所蕴含的光谱信息距离十分贴近情况下，其差值只作为空间结构信息，那么在影像与图形融合之后避免了生成较大的光谱扭曲现象[7]。运用合成后的Inew分量，需符合以下公式即

min{(P-Inew)+(Inew-I)}

(4)

其中，Inew=(P-Inew)/2。当Inew分量接近I过程中，P-Inew的数值将呈现增涨趋势，很容易导致空间分辨率出现较低的现象。当Inew分量接近R过程中，Inew-I的数值将呈现增涨趋势，光谱扭曲程度也会随之增大，光谱扭曲程度也会随之增大。基于此设置出调节值t，若1≤t<∞，那么Inew=I。若t→+∞，那么Inew=P。根据合理调节t因子的数值，获取到完美的融合结果[8]。

随后对上述公式进行改进，得出其表达式为

1≤t<+∞

(5)

从式(5)中可得出，在t=1情况下，代表Brovery融合方式，在t→+∞情况下，则代表IHS变换方式，根据调节值t进一步操控两种方式间的变化。

综上所述，通过适当改变其数值，进一步增强两者之间的对比度，突出主体和客体的分别，对所表达的具体内容予以传达，让整个画面富含美感。

3 视觉信息可视化传达

通过人眼视觉成像原则，采用映射操作，将ToF相机锥形区域中任意点投影到背景区域内，并需要保存其深度信息，从而把三维信息还原成平行光模式下的成像效果，进一步达到人眼视觉效果[9]。设计出几何映射模型，如图1所示。

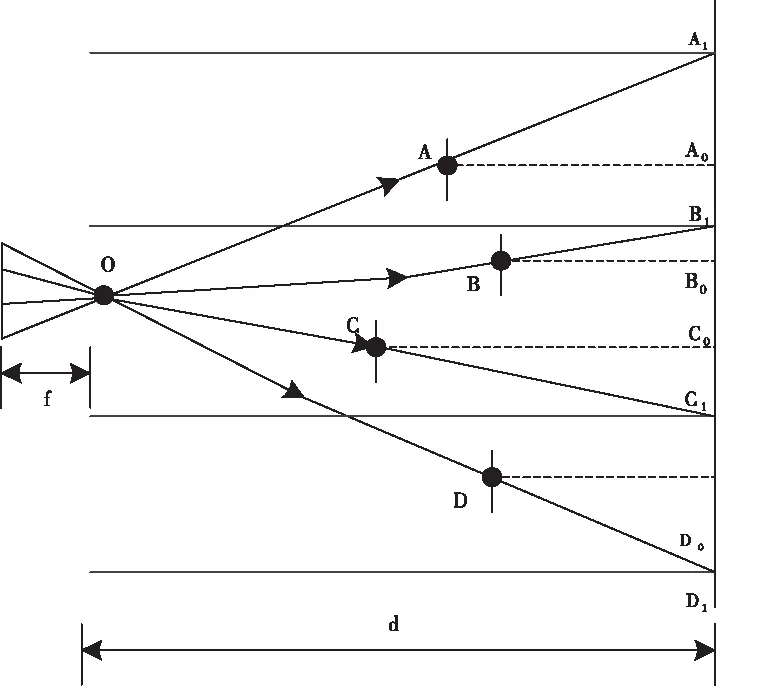
图1 几何映射模型

将图形在空间内的点全部映射至间隔相机小孔是d的ω平面当中，f表示为焦距，ToF相机当作小孔成像模型，因此在ω图形平面和ω′图形平面内只差距一个相乘系数f/d。基于视觉映射的几何模型从图2中展现。

图2 视觉映射几何模型

其中C点所描述的是模型的小孔，B点所描述的是空间内的任意点[10]。依据三维TOF采集到数据的细节信息，并获取到与B点相关联的各个坐标系的维系信息(x1，y1，r1)。设置d代表欧式距离基础上描述的深度信息，即d(CB)=r1。M为B在VA上进行映射，N为B在UA上进行映射。设置∠ACB=∠α，∠MAB=∠β。∠β所描述的是BAC和UAC之间的二面角。

依据图2能够获得以下公式即

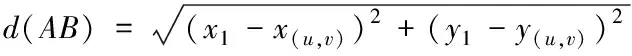
(6)

(7)

(8)

(9)

为了达到视觉的舒适性，需要在艺术图像的空间布局上合理规划，突出层次感，并保留其特点不丢失。需要将空间内各个点都映射到距离相机l(m)与光轴平行的平面ω中，然后在平面中建立坐标系，原点同样为平面与光轴的交点，坐标轴与图像水平，垂直轴平行[11]。具体内容如图3所示。

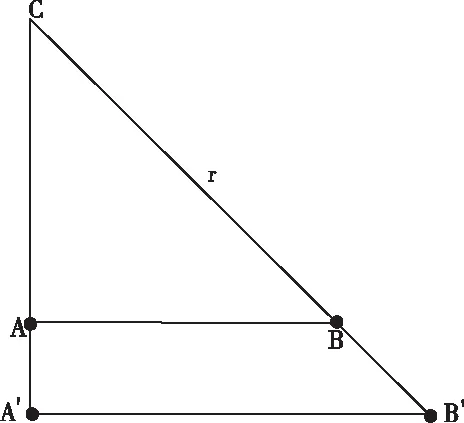
图3 视觉映射几何模型内组成的相似三角形

从视觉映射几何模型内组成的相似三角形，可得出其表达式为

d(A′B′)=ltanα/cosα

(10)

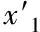
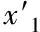
(11)

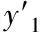
(12)

在此基础上又得出式(17)为

(13)

根据上述式(11)能够获得公式为

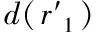
(14)

在三维相机灰度图像坐标系中的各个像素点所对应深度信息实施相对变换[12]。故能够把空间点内的坐标全部映射到ω的坐标系中。

视觉信息可视化的作用在于通过图形化手段进行清晰，有效的信息传递。取得美学形式和功能之间的平衡，从而创造出一些华丽的可视化图表。

4 仿真结果分析

4.1 实验环境

为证明所提方法可行性，需要对图像质量进行检测，在Windows10环境下构建实验平台，2.93GHZ处理器，48.0G内部储存空间，64为Windows10教育版。实验图像来源于艾瑞数据库，并将实验图像的大小设置为188×188的国际标准图像。

4.2 实验结果分析

直方图对于增强的像素不加选择，所以在增强的过程中，有可能降低图像中有用信号的对比度，使得变换后图像的灰度级减少，图像细节消失。因而对所提方法映射前后直方图进行对比。

由图4可以看出，图(b)英文字母要比原始图像矩形框内字母清晰度较高，说明在细节处直方图均衡化得到了增强。整张图片的平均亮度得到了提升，对比度得到了增强。原始图像的直方图有尖峰的，经过映射后，尖峰消失，增加了图像中有用信号的对比度。主要原因在于本文方法把三维信息还原成平行光模式下的成像效果，进一步达到人眼视觉效果。

图4 直方图增强仿真图

由图5可以看出，原始图像较暗，无法准确观测图像细节，相比于文献方法，所提方法人眼直接看到的信息含量增多，图片整体光泽度上升。

图5 仿真测试对比图

(15)

从表1中能可知，所提方法的峰值信噪比较高，证明图像质量检测精度高，较好地保留可视化图像细节信息，并有效地提升了视觉信息可视化传达与识别质量。

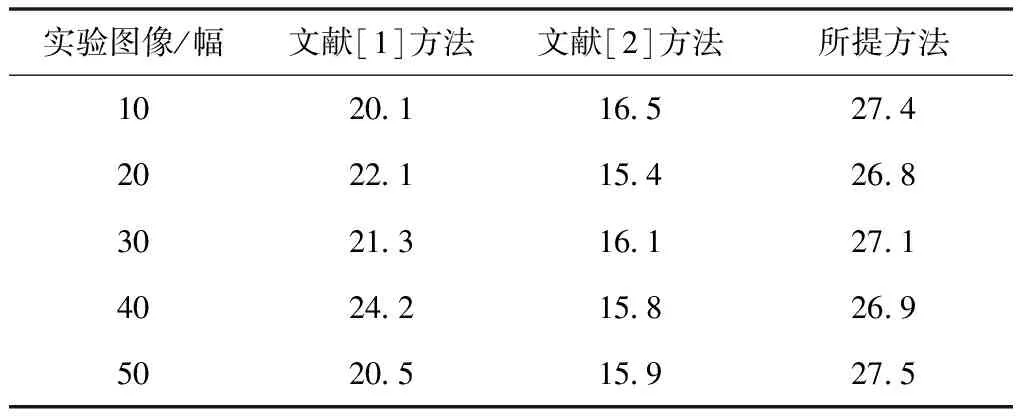
表1 峰值信噪比值对比

如果峰值信噪比的值变大，则图像的对比度增强并且在一定程度上绝对均方亮度误差减小。均方误差(MSE)表达式如下

(16)

式中，f表示输入图像，G表示输出图像，M和N表示图像的行数以及列数。

绝对均方亮度误差用来衡量图像亮度保持的程度，AMBE值越小图像亮度维持效果越好；模糊熵越大表示图像质量越高。其中，绝对均方亮度误差被定义成如下形式

AMBE=|Meanf-MeanG|

(17)

式中，Meanf表示输入图像的均值，MeanG表示输出图像的灰度均值。

从表2中可得出，相比其它方法，所提方法的均方误差、均方亮度误差以及模糊熵均满足条件，融合处理后的图像视觉信息显著性提高，所得图像信息质量更优质。主要原因在于所提方法将ToF相机锥形区域中任意点投影到背景区域内，并需要保存其深度信息，从而把三维信息还原成平行光模式下的成像效果，进一步增强了人眼视觉效果。

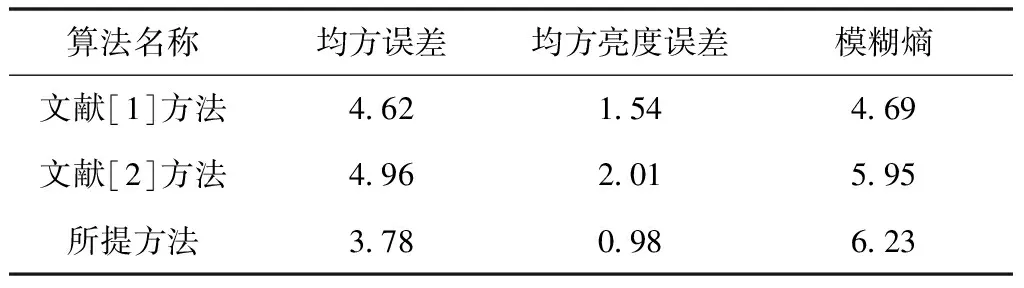
表2 影像与图形融合后的评价指标

5 结论

针对视觉信息可视化传达效果较差问题，运用所提方法，首先将IHS变换法和Brovery融合法相结合，运用调节值合理调节两者的对比度，使画面更加和谐。然后采用映射方式将空间内的全部点都映射到距离相机和光轴平行的平面中，在平行光模式下完成图像成像，从而达到有效的信息传递。仿真结果表明：所提方法逼近人类视觉效果，峰值信噪比较高，证明图像质量检测精度高，较好地保留可视化图像细节信息，且均方误差、均方亮度误差以及模糊熵均满足条件。