超空泡航行体非定常流体动力延迟效应水洞试验研究

刘喜燕，袁绪龙，王 鹰，罗 凯，汪新禹

西北工业大学 航海学院，西安 710072

0 引言

根据空泡截面独立扩张原理[1]，当航行体非定常运动时，位于空化器之后的航行体行进在独立膨胀的系列空泡截面形成的隧道中，航行体改变攻角时，新生成的空泡经过一段时间才能到达航行体尾部，改变沾湿面积，从而改变流体动力的大小。这个时间滞后，即为“超空泡航行体非定常流体动力的延迟效应”，简称“空泡延迟效应（Cavity-delay effect）”。

空泡延迟效应将在很大程度上影响主体空泡的流型和超空泡对航行体的包络性[2]。为了研究超空泡航行体的运动特性，在动力学建模时必须考虑空泡延迟效应。Kirschner 等[3]指出超空泡航行体的动力学特性展现出斜坡不连续的力学曲线和时间延迟效应，并分析了空泡延迟对航行体流体动力的影响。Goel[4]根据空泡截面独立扩张原理获取了超空泡航行体尾部滑行的非线性力，建立了考虑流体动力延迟效应的非线性动力学模型。罗凯等[5]基于超空泡的独立扩张原理，考虑了超空泡的时间延迟效应，提出了可以描述超空泡航行体机动航行特性的运动控制模型。李代金等[6]在超空泡时间延迟效应的基础上，建立了超空泡航行体空间运动模型。韩云涛等[7]针对航行体运动时存在的时滞问题，提出了一种状态空间预测控制方法，建立的预测模型对具有时滞特性的超空泡航行体控制效果良好。

如果延迟时间为零，航行体与空泡之间的相对位置关系与定常运动时相同。延迟效应的存在使得超空泡航行体动力学模型出现振荡，即尾部来回撞击空泡壁，称为“尾拍现象”。近年来，国内外许多学者针对超空泡航行体的尾拍现象进行了研究，李东旭[8]对超空泡射弹水下运动的空泡形态、尾拍运动进行了试验分析，并对射弹空化流场进行了数值模拟，模拟结果与试验结果吻合很好。何乾坤等[9]结合超空泡航行体尾拍运动与空泡变化互相耦合的特点，建立了耦合运动方程，并对超空泡摆动与尾拍的互相作用过程进行了数值模拟，得到了不同速度和角速度的超空泡航行体运动过程以及超空泡摆动对尾拍的影响规律。Kulkarni 等[10]基于滑水力模型计算航行器的尾拍受力，在忽略重力影响以及航行器以头部为中心进行旋转的假设下，建立了超空泡射弹在单平面内高速运动的动力学简易模型，并成功预报了射弹尾部和空泡壁的拍击运动。赵成功等[11-13]采用CFD 方法，通过耦合求解流场控制方程与刚体动力学方程，建立了超空泡射弹平面运动的数值计算方法，研究了射弹在不同参数影响下的空泡形态、尾拍现象和弹道特性。

综上所述，目前的研究主要集中在考虑延迟效应的动力学建模以及非定常运动尾拍过程中的流体动力特性等方面，而对非定常流体动力延迟效应的定量试验研究较少。本文通过搭建连续变攻角测力试验平台，对超空泡航行体非定常流体动力的延迟效应进行研究，为进一步研究超空泡航行体尾拍现象形成机理及动力学建模、超空泡航行体弹道特性和机动航行控制技术打下一定基础。

1 试验方法与装置

本试验依托于西北工业大学高速水洞实验室开展，提出了连续变攻角测力试验方案，用于验证空泡延迟效应对航行体流体动力的影响。该水洞为封闭式循环水洞，是开展水下航行器流体力学研究的大型基础试验平台，如图1所示。

1.1 试验方法

超空泡航行体连续变攻角测力试验系统主要由攻角调节与测量系统、通气流量控制与测量系统、流体动力测量系统、压力测量系统、图像采集系统及模型主体组成，系统结构如图2所示。

图2 试验系统图Fig.2 Diagram of experimental system

将模型以尾支撑方式安装于水洞工作段的电动转台上，通气管路、测压管路和天平导线从导流罩内孔引出至洞体外，压缩空气经流量控制器接至模型通气管。试验开始前调整模型方向，使模型保持在0°攻角位置上。自编摆动程序，由单片机控制步进电机，实现模型按设定规律连续摆动。高速摄像机安置在模型前方和模型上方，记录空泡随航行体的变化过程。

1.2 试验装置

为了开展此次试验，搭建了专用的综合测控系统，此系统可以实现通气流量控制与测量、模型攻角调节与测量、流体动力测量和高速摄像机启停控制等功能。

图像采集系统主要由两台索尼DSC-RX10M2 高速摄像机构成，由支架分别固定在模型前方和上方，透过水洞工作段的有机玻璃窗进行拍摄，相机分辨率为1920 pixel×1080 pixel，拍摄帧速为1000 帧/s。

攻角调节与测量系统主要由电动转台、步进电机、旋转编码器、步进电机驱动器、单片机、控制器、直流电源构成。测控计算机通过控制器向步进电机驱动器发送指定频率的脉冲和转向信号；驱动步进电机以指定速度和方向转动，进而驱动电动转台带动模型按照指定规律转动，从而实现攻角的连续调节动作。旋转编码器则持续向测控计算机反馈其测量所得的模型旋转角度。

流体动力测量系统主要由内置高精度三分力天平和NI9237 应变数据采集器构成。天平总长120 mm，直径20 mm；量程为轴向力±7 kg，侧向力±5 kg，力矩±1 kg·m，精度5‰。通气流量控制与测量系统主要由ALICAT 质量流量控制器组成。该流量控制器量程为0～100 SLPM（标准升每分钟，1SLPM=0.06 m3/h），精度为满量程的1%；采用自编通气流量控制软件实现通气流量的定时定量控制，且通气过程中的实际流量参数由控制器实时采集并记录。

2 试验模型

试验模型采用小长径比超空泡航行体外形，空化器直径为19 mm，柱段直径为54 mm，空化器前端面到圆柱段尾端面为362.7 mm。整套模型由空化器、圆锥段、圆柱段、尾喷管、整流罩和立支杆6 部分组成，其中空化器为可更换的独立构件。空化器前端面后方开有一圈通气孔，压缩空气由PU 管引入航行体前锥段后经过空化器后方的环状缝隙，沿着航行体轴线方向往空泡内补气。在航行体肩部和圆柱段距尾部22.0 mm 处分别开有测压孔，用PU 管将此处的压力引出洞体外测量。立支杆安装在电动转台上，带动模型转动。试验模型的内部结构和安装分别如图3 和4所示。

图3 模型内部结构图Fig.3 Internal structure of the model

图4 试验模型总装图Fig.4 General assembly drawing of the experimental model

3 试验结果与分析

本文开展了水流速度、空化器舵角和摆动频率等参数对流体动力延迟效应的影响规律试验，研究真实状态下的流体动力延迟效应。试验工况如表1所示。

表1 试验工况Table 1 Experimental conditions

试验开始前，通过调节压缩空气流量来控制空泡形态，确定在标准工况下通气流量为80 SLPM。在试验的通气过程中，水洞压力会逐渐升高，洞体内压力通过控制系统自动控制并稳定在80 kPa 左右。

试验中，为消除通气流量和水洞水流速度的脉动变化带来的误差，保证结果的准确性，每个工况均做重复试验。通过模型的运动角度与侧向力数据对比来分析出现的延迟效应，计算各个运动周期下角度峰值与流体动力峰值之间的时间差Δt，取均值作为该次试验的流体动力延迟时间。对多次重复试验得到的延迟时间数据取均值，作为该工况下的流体动力延迟时间t。

为方便对比分析，对延迟时间进行无量纲化处理。取航行体长度L=432 mm 为参考长度，水流速度v为参考速度，则参考时间表达式如下：

其物理含义是流体介质流经航行体长度所需的特征时间。以各工况的平均延迟时间t'除以参考时间tck可得一无量纲参数，定义为延迟系数Cyc。

3.1 空泡生成及变化过程

图5 给出了工况4 在连续变攻角测力试验过程中的空泡变化过程。可以看出，从时序1 到时序5 完整地展示出了空泡的生成过程。时序1，试验开始，启动水洞达到试验水速要求。时序2，通气系统启动，开始通气，可以看到模型头部开始出现水汽混合的云状空泡。随着通气量的增加，空泡在时序3～4 进一步发展。在时序3 可以清晰地看到空化器形成的空泡中存在明显的回射流冲刷模型壁面，模型尾部开始出现空化。时序4，空泡发展到尾部，与尾部空泡开始融合，最终发展为时序5所示的闭合在尾喷管的完整透亮的超空泡。

图5 空泡生成及变化Fig.5 Generation and variation of cavity

为了更直观地看到摆动时空泡的延迟效应，在图6 中给出了模型上方高速摄像机拍摄的空泡图，图中的黑线为模型中轴线位置。可以看出，时序1，空泡刚生成，关于中轴线对称。之后，模型开始摆动，时序2～4 为模型摆动到一侧后又回到中轴线的过程。对比时序2 与3 的空泡图，可以看出模型在时序2 摆动到达预设位置，空泡发生延迟，在时序3 才产生与模型位置相对应的空泡。时序4，模型回到中轴线位置，与时序1 的图像对比发现，此时空泡不对称，同样发生了延迟。之后的时序5～7 为模型摆动到另一侧后又回到中轴线的过程，同样可以明显地观察到时序2～4 中的空泡延迟效应。

图6 摆动过程中空泡变化Fig.6 The change diagram of cavity during oscillation

3.2 水流速度影响分析

工况1～4 分别针对不同的水流速度展开研究，试验结果如图7所示。图中Fz–1 和Fz–2 分别为两次重复试验中航行体模型所受到的侧向力，Angle 代表摆动角度，可以明显看出，不同工况下侧向力的大小存在明显差异。

以工况4（图7（d））为例进行分析，结合空泡图可以看出，在模型未摆动前，空泡处于稳定状态，模型被完整地包裹在空泡内，此时侧向力基本不存在。随着模型开始朝一侧摆动，尾部迎流面出现沾湿，侧向力开始逐渐增大。当模型摆动到最大幅值后开始回摆，由于空泡形态发展相对于姿态改变的延迟特性，沾湿面积会继续增大，侧向力继续增大，但变化率开始降低。当侧向力达到峰值时，模型已经摆回，侧向力的峰值滞后于模型摆动角度的峰值。

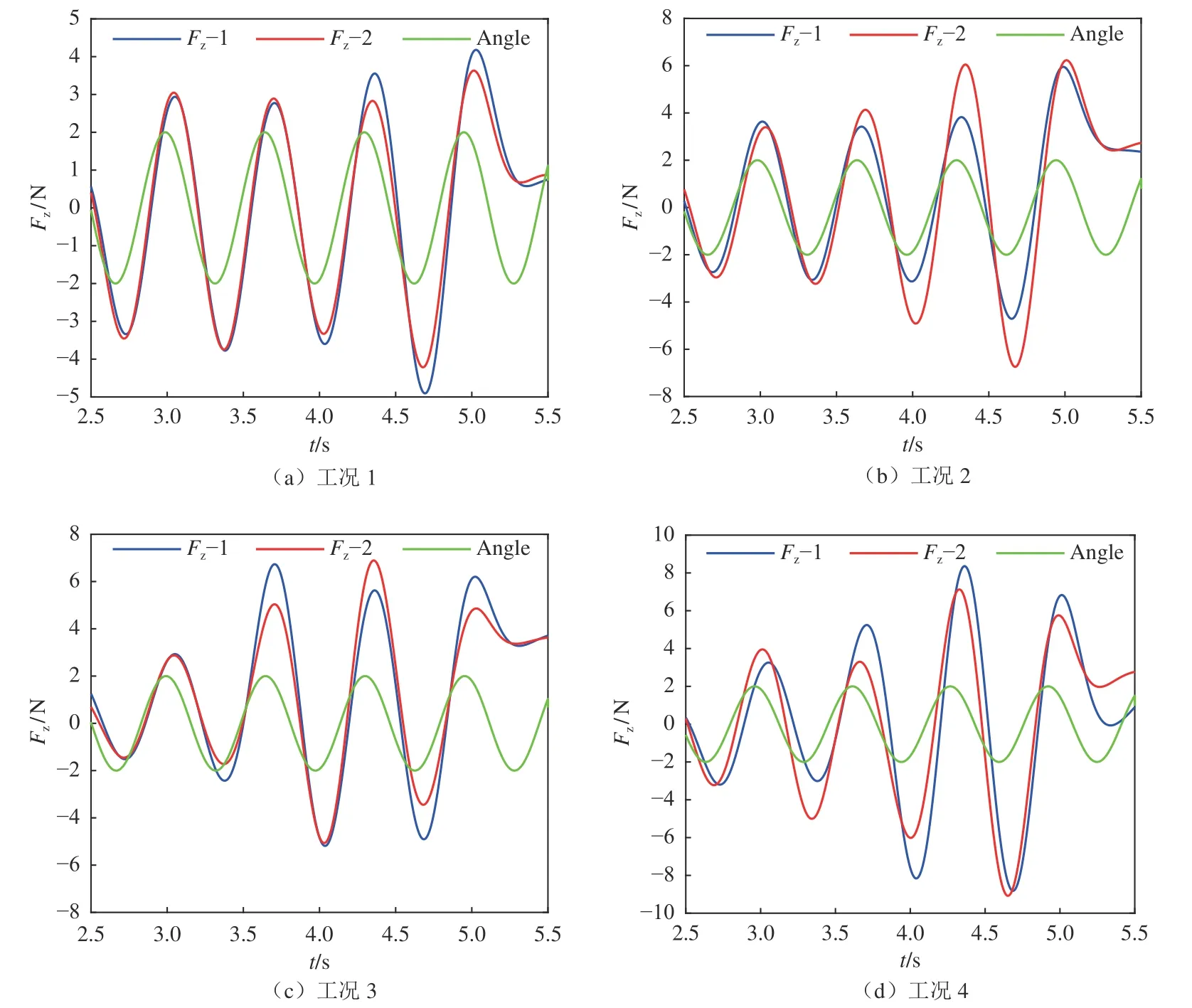
图7 试验结果Fig.7 Experimental results

随着模型继续回摆，附体空泡发展，圆柱段的沾湿面积持续减小。当模型摆动到初始位置时，尾部仍然存在部分沾湿，侧向力不为零。之后模型向另一侧继续摆动，空泡发展至完全包裹模型，侧向力减小至零。随着摆动的继续，出现沾湿且面积逐渐增大，侧向力随之增大。当摆动达到最大幅值时，侧向力同样并未达到峰值，侧向力的峰值仍然滞后于模型摆动角度的峰值。之后几个周期的变化类似，故不再赘述。

表2 给出了不同水流速度下的流体动力延迟时间和流体动力延迟系数。

表2 不同水流速度下延迟时间对比Table 2 Comparison of delay time at different water velocity

图8 给出了延迟系数随水流速度的变化规律。可以看到，空泡引起的流体动力延迟时间近似为水流过航行体全长的时间，水流速度越高，延迟系数越大，与水流速度近似成线性关系，拟合关系式见图8。从宏观上看，模型处于静止状态时，空泡稳定，泡内流场结构近似于层流。当模型开始摆动，其产生的影响可以分为轴向扰动和侧向扰动，使得泡内流动从近似层流状态向湍流状态改变。空泡形状改变的滞后正是由于扰动经水介质传播需要时间造成的。水流速度越高，摆动时产生的扰动越大，空泡形状改变所需要的时间越长，延迟时间就越长。

图8 延迟系数随水流速度的变化规律Fig.8 Variation of time-delay coefficient with water velocity

3.3 空化器舵角影响分析

空化器舵角使流场环境更加复杂，根据已有的研究经验，在同一摆动周期，不同的运动方向会导致流体动力的不对称分布。考虑到试验条件和数据处理过程可能会丢失某些特征，对工况5 和6 各安排4 次重复试验，试验结果分别如图9 和10所示。

图9 工况5 试验结果Fig.9 Results of Case 5

对试验结果进行数据处理，并与预置舵角为0°的工况4 的试验结果进行对比，得到空化器不同舵角下的流体动力延迟时间和流体动力延迟系数，如表3所示。

图10 工况6 试验结果Fig.10 Results of Case 6

表3 空化器不同舵角下的延迟时间对比Table 3 Comparison of delay time at different rudder angle

延迟系数随空化器舵角的变化规律如图11所示，可以发现在试验的预置舵角范围内，随着预置舵角的增大，延迟时间增加。延迟系数与舵角近似成线性关系，拟合关系式见图11。

图11 延迟系数随舵角的变化规律Fig.11 Variation of time-delay coefficient with rudder angle

空化器预置舵角的存在使得航行体周围流场呈现不对称分布，导致空泡截面变形，从而出现斜流。舵角越大，空泡的倾斜越大，航行体尾部就越容易出现沾湿。沾湿时，空泡边界与尾部壁面的碰撞必然会导致空泡内流场变复杂、扰动增大，空泡形状改变所需要的时间增加，即延迟时间增加。

3.4 摆动频率影响分析

航行体的摆动频率作为决定航行状态的另一个重要特征参数，与超空泡航行体非定常流体动力的延迟特性密切相关。在一定程度上，可以用航行体连续往复摆动来类比航行体在超空泡状态下自由航行过程中发生的尾拍现象。试验针对1.00 和1.53 Hz摆动频率的延迟特性进行了研究。对摆动频率为1.00 Hz 的工况7 安排了2 次重复试验，试验结果如图12所示。侧向力的变化规律与工况4 类似，在之前已经进行了详细的分析，这里不再赘述。数据处理后，与摆动频率为1.53 Hz 的工况4 的试验结果进行对比，得到不同摆动频率下的流体动力延迟时间和流体动力延迟系数，如表4所示。

表4 不同摆动频率下延迟时间对比Table 4 Comparison of delay time at different oscillation frequency

图12 工况7 试验结果Fig.12 Results of Case 7

延迟系数随摆动频率的变化规律如图13所示。通过数据的对比可以看到，在试验设置的摆动频率范围下，摆动频率越大，延迟时间越少。

图13 延迟系数随摆动频率的变化规律Fig.13 Variation of time-delay coefficient with oscillation frequency

由于航行体摆动频率发生变化，空泡随航行体位置改变进行状态更新的频率也发生变化。摆动频率越大，即摆动周期越小，对流场产生的扰动间隔越小，空泡延迟时间相应的也越少。

4 结论

本文通过连续变攻角测力试验，测量并分析了超空泡航行体的空泡及流体动力的延迟效应，在水洞试验条件下获得了水流速度、空化器舵角和摆动频率对延迟效应的影响规律，得到以下结论：

1）在航行体摆动过程中，模型尾部会出现反复沾湿，内流场变复杂，从拍摄图像中可以明显观察到空泡的延迟效应。

2）水流速度越高，摆动时产生的扰动越大，空泡形状改变所需要的时间越长，即延迟时间越长，延迟时间约为水流流经模型全长的时间，且延迟系数与水流速度近似成线性关系。

3）在试验预置舵角范围内，随着预置舵角的增大，航行体尾部出现沾湿，扰动增大，空泡形状改变所需要的时间增加，延迟时间增加，延迟系数与舵角近似成线性关系；在试验设置的两个摆动频率下，摆动频率越大，延迟时间越少。