基于时空浓度梯度反演扁平微通道中平均流速的优化算法

吴斯达，陈柯洁，曾 效，李泳江，覃开蓉

大连理工大学 光电工程与仪器科学学院，辽宁 大连 116024

0 引言

近年来，随着微流控芯片技术在化学、生命科学、医学等相关领域的广泛应用，微流控通道内流体的定量检测与精确操控已成为重要的研究热点[1]。速度是流场最主要的特征参数之一，因此微流控通道内流速的测量对于研究微量多相流体的精准操控、构建复杂的离体生物力学微环境、控制生化反应过程等都具有重要意义[2-4]。高度远小于横向和纵向几何尺寸的扁平微通道是最常见的微通道结构形式，其高度方向的平均流速测量是定量分析壁面剪切力和物质输运规律的前提[5-7]。

常见的流速测量方法是通过测量粒子跟随流体的运动来实现，例如微尺度粒子图像测速法（micro-PIV）和微尺度粒子跟踪测速法（micro-PTV）。前者通过连续拍摄记录流场中的粒子群，比较相邻时间间隔的粒子群位置变化来计算流体速度[8]；后者采用拉格朗日类方法直接测量分析单个粒子的运动，避免了micro-PIV 的平均效应，实现了更高的空间精度[9-10]。但这类基于粒子的测速方法在测量小尺度结构时存在较大误差，因为测量小尺度的流动特性需要较大的示踪粒子浓度，但过大的粒子浓度会引发激光穿透困难等问题。此外，这类方法的测量精度还受示踪粒子跟随性的影响[11-13]。随着光学技术的快速发展，科研人员提出了点检测扫描方法[14]。该方法利用光学仪器对准激光进行强聚焦，可以实现高分辨率的单点速度测量，但对系统的校准精度要求较高，且设备昂贵、操作复杂。常见的测量方法还有标量图像测速法，其原理是从守恒标量（如浓度、厚度）的观测中获取速度[15]。与基于粒子的测速技术相比，该方法不存在由粒子尺寸带来的流场干扰和跟随性误差，可以更精确地实现流速测量，已被广泛应用于湍流研究和天气预报[16-17]；而在微流控通道内主要是低雷诺数的层流，标量图像的时空分布必然受流体对流-扩散的共同作用，特别是在扩散占优的流动条件下，标量场的时空梯度分布与流场之间的耦合关系变得相对复杂，如何依据标量场的时空分布确定微通道内的流体流动信息及相关影响因素尚有待于进一步研究。

为实现扁平微通道内流速的精确测量，本文以标量图像测速法为基础，结合微通道内物质输运原理，提出了一种基于时空浓度梯度反演扁平微通道中平均流速的优化算法。通过光学成像技术获得微通道内物质的时空浓度梯度，利用扁平微通道结构特点，基于Taylor-Aris 弥散方程得到描述物质浓度与平均流速间的定量关系，结合优化问题中最小化目标函数的思想，计算得出扁平微通道内流体的平均流速。通过数值仿真验证该优化算法在无噪声条件下的可行性和精度，分析噪声条件下输入浓度信号和物质扩散系数对算法求解准确度的影响。最后利用提出的方法分析微通道中物质浓度图像的时间序列，将优化算法反演得到的流速与流量传感器测量计算结果进行比较，验证算法的可行性和准确性。

1 基于浓度场反演流速的方法

为了获得微通道内浓度场与平均流速之间的定量关系，首先基于Navier-Stokes 方程和Taylor-Aris 弥散方程构建流道模型并进行理论分析。待检测的扁平直通道如图1所示，其高为H，宽为W，长为L。

图1 扁平直通道示意图Fig.1 Schematic of a straight shallow microchannel

1.1 直接反演法

1.2 优化算法

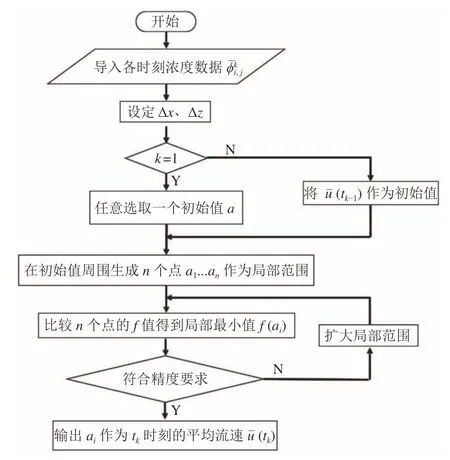
图2 优化算法流程图Fig.2 Flow chart for the optimization algorithm

2 数值仿真

2.1 微通道内时空浓度分布

为了研究基于浓度分布反演流速的方法，首先构建了微通道内物质时空浓度分布。以扁平微通道为例构建如图1所示微通道，其长度L为3 cm，宽度W为3 mm，高度H为150 μm。在微通道内给定均匀分布的流速条件，按其形式可分为定常流和脉动流。在脉动流情况下，流速以正弦波形式变化，满足其中为速度信号的平均值，λ2为速度信号的振幅，f2为速度信号的频率。将通道始端正中间宽度为1 mm 的区域作为入口，向其通入浓度动态变化的组分，其浓度以正弦波形式变化，满足其中为浓度信号的平均值，λ1为浓度信号的振幅，f1为浓度信号的频率。通过MATLAB 程序求解式（8），将速度作为已知量迭代求解浓度分布，边界条件设为左右壁面和微通道出口处无浓度梯度，即可得到微通道内时空浓度分布情况。图3 为脉动流入口浓度条件下物质在微通 道内传输5 s 和10 s 后的浓度分布。

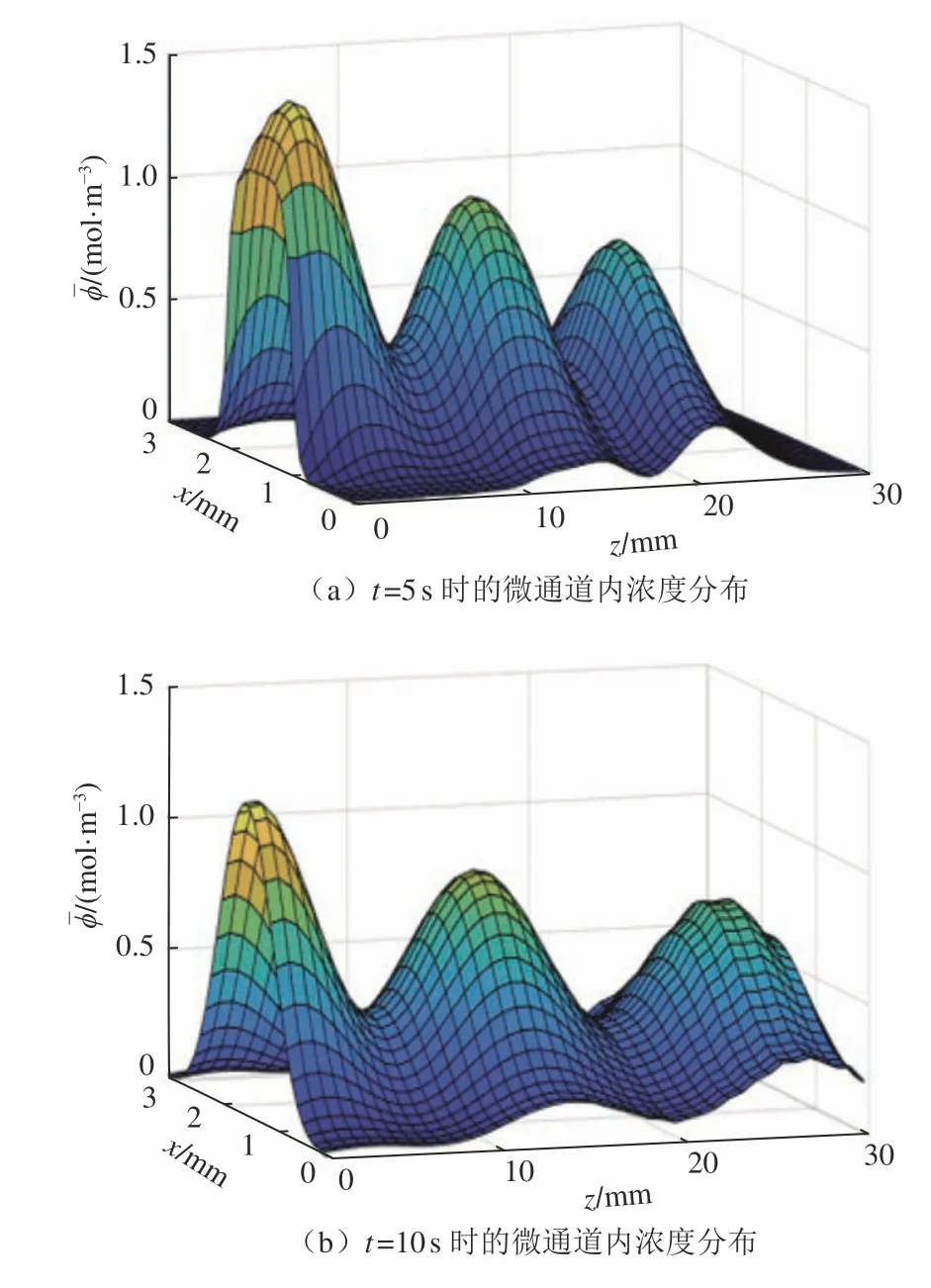
图3 微通道内浓度分布仿真结果Fig.3 Simulation results of the concentration distribution in the microchannel

2.2 无噪声条件下流速反演

基于构建的微通道内时空浓度分布，分别在定常流和脉动流条件下，对无噪声存在时以直接反演法与优化算法计算平均流速的方法进行了验证。基于动态浓度信号在定常流中的浓度分布，图4（a）给出了直接反演法和优化算法计算得到的平均流速与真实流速的比较结果。结果表明：直接反演法所求流速在浓度信号处于极值点时有明显误差。原因是当浓度处于极值点时，浓度对时间的导数为零，式（10）中ci存在较大误差；此外，一元二次方程的求解存在除法运算，分母ai的微小波动也会对结果产生较大影响。相比之下，由优化

算法求得的流速与真实流速几乎完全重合，相对误差ε=0.001%。在脉动流情况下（图4（b）），直接反演法所得流速在特定点处仍存在较大的计算误差，而由优化算法求得的平均流速与真实流速的相关系数R=1，相比于直接反演法有更高的反演精度。

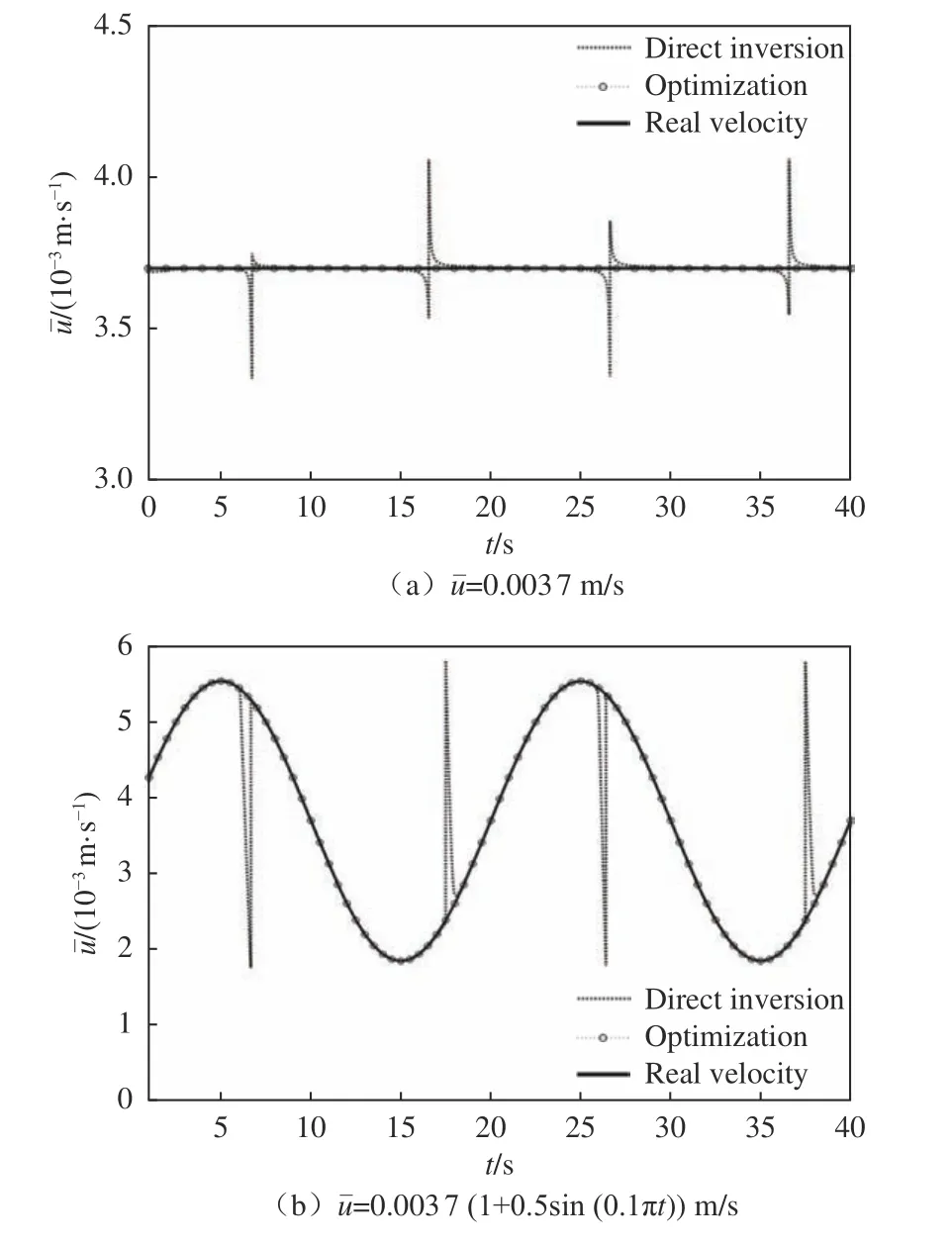
图4 直接反演法和优化算法求得平均流速与真实流速对比Fig.4 Comparison between the real velocity and the average velocity derived based on the direct inversion method and the optimization algorithm

2.3 有噪声条件下流速反演

由于实验中测得的时空浓度分布通常存在噪声，因此本节讨论噪声条件下物质浓度信号的频率、振幅和物质扩散系数对流速求解的影响。通过在浓度数据中添加0.1% 的白噪声来模拟实验测得浓度数据中的噪声。

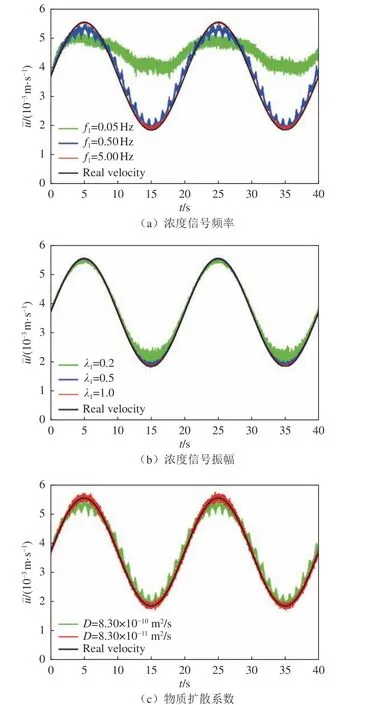
图5 浓度信号参数对优化算法反演平均流速的影响Fig.5 Influence of parameters of the concentration signals on the average velocity derived by the optimization algorithm

由仿真结果可知：在噪声条件下，增大物质浓度

信号的频率和振幅、选择扩散系数较小的物质可以提升优化算法的准确度。

3 实验验证

3.1 实验装置与方法

实验装置如图6所示，主要包括物质浓度时空梯度生成装置、具有扁平微通道的微流控芯片、倒置荧光显微镜和废液回收装置。实验中组合使用恒流泵和工控计算机控制的压力泵作为浓度梯度生成装置。

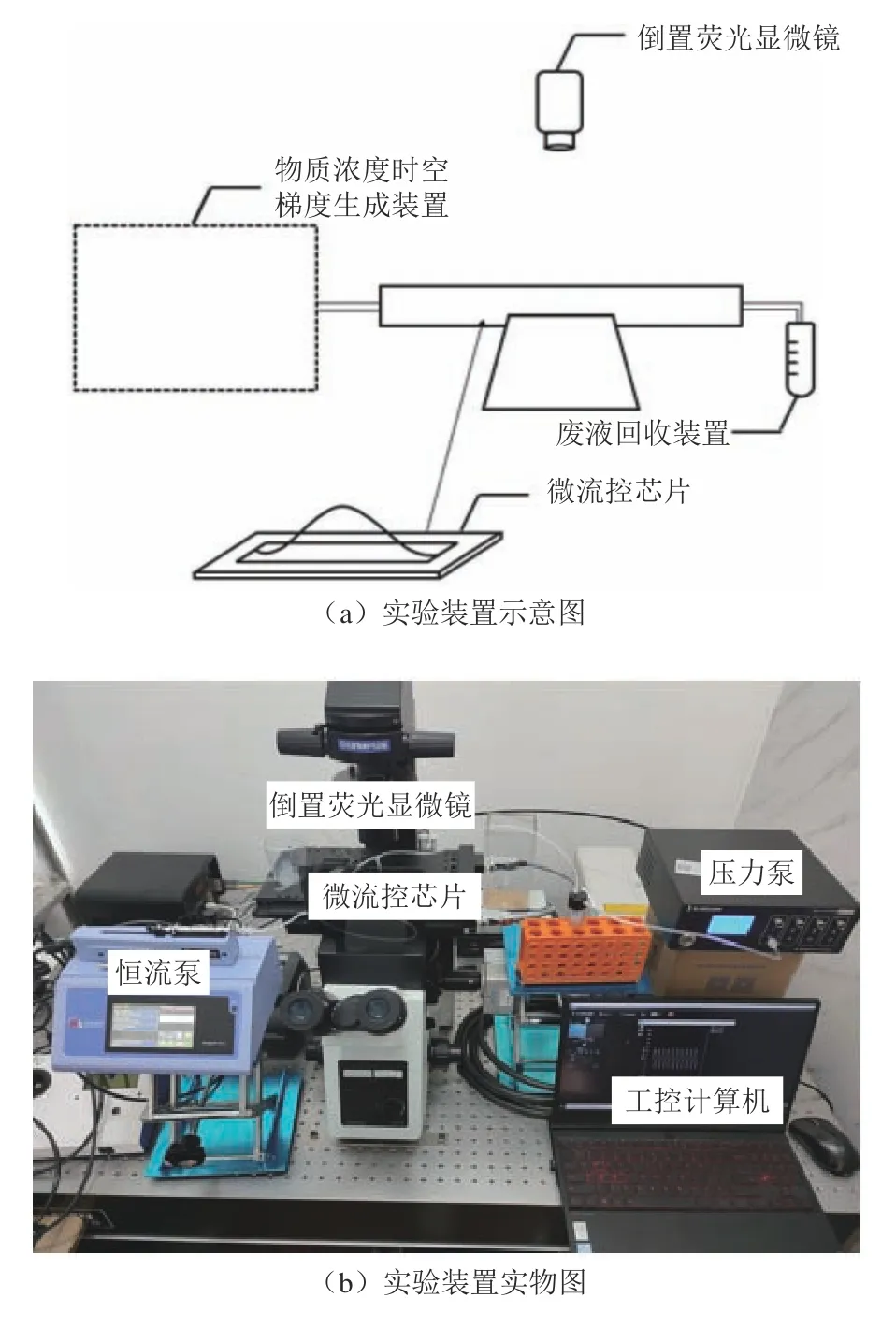
图6 实验装置图Fig.6 Experimental setup

利用该装置确定扁平微通道内平均流速包括以下步骤：在压力泵配套的储液管内加入摩尔浓度为5 ×10–6mol/L 的罗丹明溶液，其扩散系数为4.14×10–10m2/s，在恒流泵的注射器中加入去离子水，通过调节参数控制两泵，使其体积流率随时间按照一定规律变化，进而在微通道的入口处产生摩尔浓度随时间变化的罗丹明溶液，由于横向分子扩散效应，最终在扁平微通道中产生时空浓度梯度。待废液回收装置出现液体后，利用倒置荧光显微镜记录距离微通道入口一定长度处的测量视野内不同时刻的罗丹明溶液摩尔浓度分布，进而得到时间间隔为Δt的一

系列荧光图像，如图7所示。最后对所得图像进行处理：取不同时刻相同区域的荧光图像，提取灰度值并转化为对应摩尔浓度值后代入优化算法式子中，设置优化参数进行计算，即可得到不同时刻下微通道内的平均流速。

图7 实验方法示意图Fig.7 Schematic of experimental method

3.2 实验结果

实验时采用的直线型微通道几何尺寸如下：长度4 cm，宽度4 mm，高度80 μm。将距离微通道入口2 cm 处作为显微镜观测位置，照片拍摄帧率为13.407 Hz，空间分辨率为4 μm/pixel。实验时拍摄的荧光图像如图8所示。

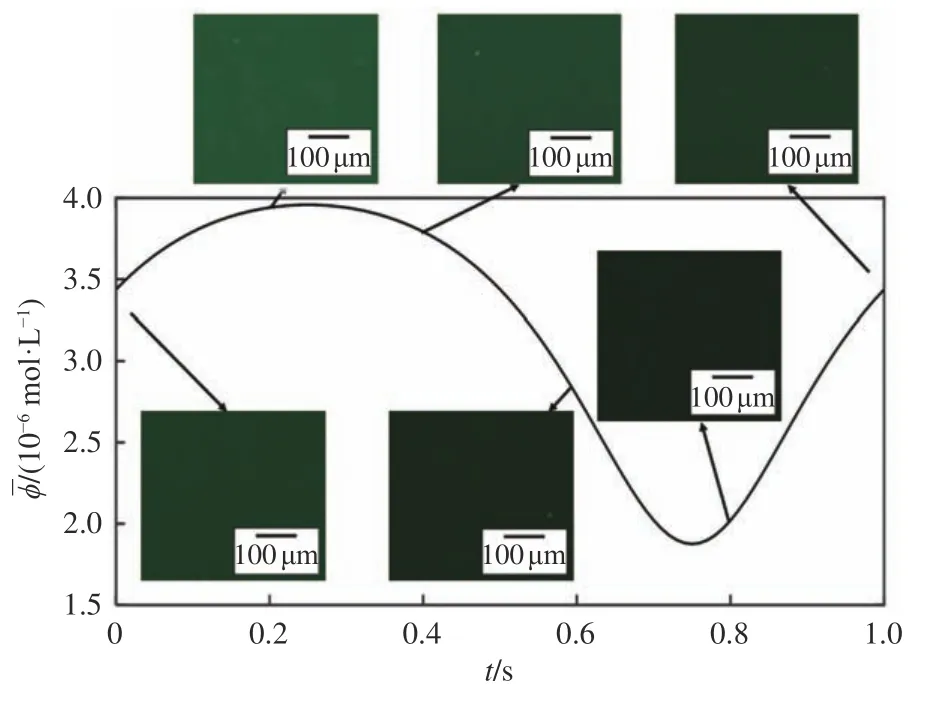
图8 实时荧光图像Fig.8 Real-time fluorescent images

提取实验所得图像序列的灰度值，进行滤波降噪处理并转换为对应浓度值，代入优化算法式子中求解微通道内的平均流速。在相同条件下利用流量传感器测量微通道内的实时流量，用测量结果除以微通道横截面积得到微通道内的流速。将上述两种方法测得的流速结果进行对比，如图9所示。可以看出：优化算法所得流速与使用传感器测量计算的结果基本一致，速度变化的频率预测准确，幅值存在一定误差，相关系数为0.9814。

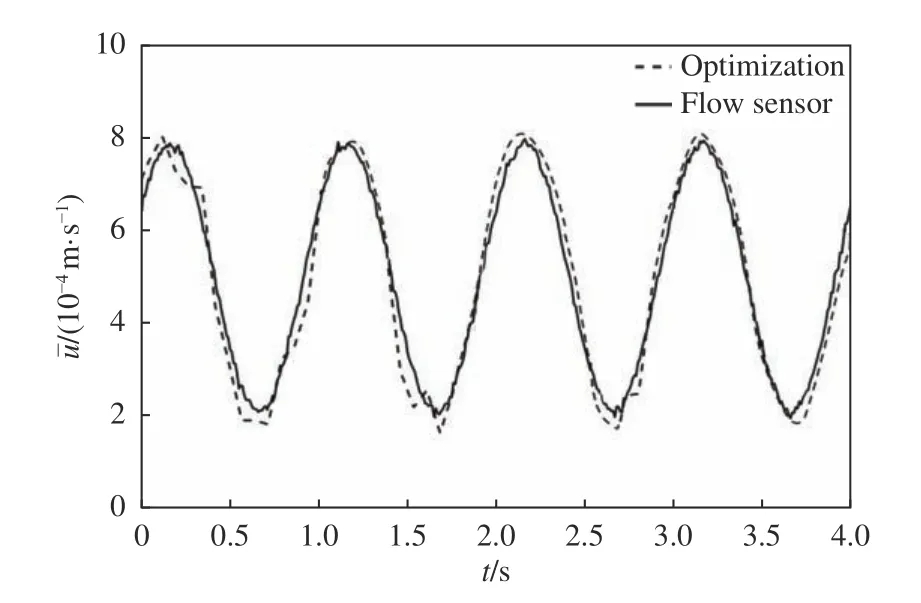
图9 优化算法与流量传感器测量计算结果对比Fig.9 Comparison of the average velocity derived by the optimization algorithm and the experimental measurement by the flow sensor

4 结论

本文提出了基于时空浓度梯度反演扁平微通道中平均流速的优化算法。无噪声条件下优化算法反演结果几乎无误差；噪声条件下，增大浓度信号的频率与振幅、采用扩散系数较小的物质可以提升算法的准确度；优化算法反演结果与流量传感器测量计算结果进行比较，相关系数为0.9814。本文提出的方法操作简便、精度较高，是一种行之有效的微通道流速测量手段。