基于法向量区域聚类分割的点云特征线提取
史红霞 王建民
太原理工大学矿业工程学院,太原,030024
0 引言
随着三维扫描技术的飞速发展,点云模型已成为几何模型的通用表示形式,并广泛应用于计算机可视化、逆向工程、三维重建、文物保护等领域[1-5]。特征是反映点云模型几何外观的最小基元,可精准地表达三维模型表面特性和几何形状[1],因此,特征提取已成为点云数据处理中的一个基础环节,如何有效准确地提取模型特征是当前点云数据处理的关键。
为解决点云模型特征提取问题,部分学者通过点云局部邻域特性及几何特征提取模型特征。几何特征主要指点间距离特征、角度特征及点云法矢、曲率等信息。文献[6]采用空间距离和角度特性提取车辆行驶道路和矿井道路边界,具有一定的准确性,但未考虑道路障碍物的影响。文献[7-8]利用点云法向量信息识别特征点,但均未考虑法向量估算的准确度。文献[9]通过对各点局部邻域协方差矩阵特征值的区域增长生成分割带,在各分割区域内根据主方向提取特征点。文献[10]引入多尺度分类算子分析局部邻域点,计算不同尺度下采样点成为特征点的概率,但多尺度使其计算效率下降。文献[11]根据曲率突变点隐含特征点,设置突变点比率选取备选特征点,但由于比率具有不确定性,故可能会造成细节特征的缺失。
基于点云局部邻域特性及几何特征的方法大多依赖全局阈值进行特征点识别,全局固定阈值的设置易造成特征点的误判或漏判,为此,有些学者运用聚类分割或局部曲面网格重建的方法识别特征点。例如,文献[12]对各点局部邻域三角区域的单位法向量进行高斯映射,对映射点进行聚类分析获取特征点;文献[13] 通过对遗迹碎片表面法向量的聚类实现碎片分割,结合法向量和碎片表面粗糙度提取边界线;文献[14]对已标记的潜在谷脊点构建局部几何特征信息三角网格,然后再进行谷脊点识别,该方法计算复杂度较高。
上述两类方法均不易准确完整地提取所有模型特征点,尤其是模型过渡特征。为此,有些学者引入数学形态学[15]、投影映射[16]、切片技术[17]、神经网络[18]、张量投票理论[19]等方法,使某些模型特征提取效果达到最优。
本文针对现有模型过渡线及细节特征线提取不完整问题,基于区域分割思想进行特征线提取,在综合利用主成分分析(principal component analysis,PCA)法、萤火虫算法[20](firefly algorithm,FA)和模糊C均值(fuzzy C-mean, FCM)聚类算法[21]对点云模型进行聚类分割的基础上,将各分割块边界点作为备选点集识别特征点,采用三次B样条法拟合生成特征线[22]。
1 FCM聚类算法
已知n个l维空间数据集S={s1,s2,…,sj,…,sn}⊂Rl,将数据集S划分为c(2≤c≤n)个子集,即聚类数为c,各子集聚类中心C={C1,C2,…,Ci,…,Cc}。最佳聚类准则是极小化目标函数值,使具有相似特征的数据点聚为一类。目标函数Jm的一般定义如下:
(1)
dij=‖sj-Ci‖Uij∈[0,1]
式中,dij为空间数据集S中第j个样本点sj与第i个聚类中心Ci的欧氏距离;m为模糊加权指数;Uij为第j个样本点属于第i个聚类中心的隶属度。
目标函数Jm取极小值的约束条件是
最小化Jm过程中,可运用下式计算隶属度和更新聚类中心:
(2)
(3)
式中,dgj为空间数据集S中第j个样本数据点sj与第g个聚类中心Cg的欧氏距离。
FCM聚类算法的基本思路就是通过不断迭代更新隶属度Uij和聚类中心Ci,使目标函数Jm最小,然后依据Jm最小时的隶属度矩阵划分数据集S。
运用常规的FCM聚类算法对点云模型进行分割进而提取特征线时,需要考虑两个问题。首先,若直接利用各点空间坐标信息进行聚类划分,则所得模型分割线将与模型特征线无直接联系,不易于后续特征线提取,为此,引入自适应邻域的主成分分析(PCA)法[23]求取模型各点法向,以各点法向量方向的接近程度为聚类特征实现点云模型的有效分割。其次,由于初始聚类中心选择的随机性以及梯度下降式的最优解搜索法,致使算法容易陷入局部最优,为解决这一问题,在FCM聚类算法中引入FA算法,利用具有全局搜索能力的FA算法为FCM聚类算法选取最优初始聚类中心,有效解决其对初始值敏感及过早收敛的问题。
2 基于法向量估计的FA-FCM组合聚类算法
法向量是散乱点云模型的一个重要属性,可用来描述模型特征信息。点云模型中任意采样点局部区域较为平坦时,邻域内各点法向量变化平缓;相反,采样点局部区域起伏变化时,各点法向量变化较大,因此,可估算模型法向量,进而提取模型特征点。
2.1 法向量估计
目前,在常见的点云法向量估计算法中,PCA方法因其算法简单高效、稳定性强而被广泛使用。PCA算法实质是对点云数据局部邻域的主成分分析,然而,固定邻域尺寸的选择致使其估算结果不精确。以二维情况(三维类似)为例,说明因邻域值选择不合理而造成的法向量估算偏差问题,如图1所示。

图1 局部邻域值大小对法向量估算的影响Fig.1 Effect of neighborhood size on normal estimation
图1中圆形区域代表邻域范围,虚直线代表虚线圆形邻域内数据拟合形成的直线,虚线箭头表示根据虚线圆形邻域范围计算所得的法向量,实直线代表实线圆形邻域内数据拟合形成的直线,实线箭头表示根据实线圆形邻域范围计算所得的法向量。图中点s1为尖锐特征点,应选择较小的邻域值拟合估算该点法向量,故图中s1点处虚线法向量因邻域值过大而造成偏差,而s2点所在区域较为平坦,只有局部略微凸起,应选择较大的邻域值拟合估算该点法向量,故图中s2点处实线法向量因邻域值过小而造成偏差。为解决这一问题,采用点云局部邻域几何维度特征最优邻域选择法[23]查找各点最优邻域值,然后结合PCA算法估算各点法向。
对点云样本数据集而言,空间维度l的值为3,此时,点云样本数据集S={s1,s2,…,sj,…,sn}⊂R3,j=1,2,…,n,n为样本总点数,取数据集S中任意样本点s,其k近邻域点集Ns={s1,s2,…,sb, …,sk},b=1,2,…,k,点s的协方差矩阵可表示为
(4)
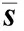
由于协方差矩阵M为对称正定阵,因此其特征值λ0、λ1、λ2具有非负性,同时,可用三个特征值描述样本点局部邻域维度特性,其特性如下:
(1)当λ0≫λ1,λ2>0时,局部邻域呈线性特征分布。
(2)当λ0,λ1≫λ2>0时,局部邻域呈平面特征分布,此时最小特征值λ2所对应的特征向量即为邻域点法向量。
(3)当λ0≈λ1≈λ2时,局部邻域呈三维曲面特征分布。
根据各样本点局部邻域维度特性可定义其特征模型:
(5)
式中,a1、a2、a3分别表示当前点局部邻域为线性(一维)、平面(二维)和曲面(三维)特征。
基于信息熵理论,依据上述维度特征模型定义点s的近邻点数为k时信息熵函数:
(6)

结合上述基于信息熵理论的自适应邻域选择法,采用PCA方法进行法向量估算,步骤如下:
(1)对于点云样本数据集S中任意采样点s,设置邻域搜索上下限值分别为kmax和kmin(kmax,kmin均表示邻域点数),搜索步长为1,初始化邻域值k←kmin。

(3)设置搜索邻域值k←k+1,当k≤kmax时,返回步骤(2);否则执行下一步。

2.2 FA-FCM组合聚类算法
为解决传统FCM聚类算法因随机性的初始聚类中心选择法造成的算法过早局部收敛问题,引入FA,将每只萤火虫的位置作为聚类中心,通过比较萤火虫亮度值进行算法迭代循环,从而为FCM聚类算法寻找最优初始聚类中心。在已求解模型法向的基础上,介绍引入FA算法后FCM聚类算法的初始聚类中心选择方法。
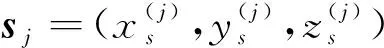
通常情况下,模糊加权指数m为2,对点云模型法向量进行聚类划分时,距离d(vj,Ci)和隶属度Uij的表达如下:
(7)
(8)
则改进后的模糊聚类目标函数为
(9)
FA算法是寻找亮度最亮的萤火虫个体,其中亮度和吸引度是该算法的两个重要概念[24],而FCM聚类算法旨在寻找目标函数最小时的聚类中心,因此,萤火虫亮度值可定义为
(10)
萤火虫吸引度为
β=β0exp(-γr2)
(11)
式中,r为两萤火虫间距离;β0为最大吸引度,即r=0时的吸引度;γ为介质对光的吸收因子。
两萤火虫A、B间距离为
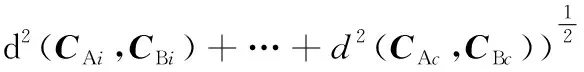
(12)
i=1,2,…,c
式中,CAi、CBi分别为萤火虫A和萤火虫B的第i个聚类中心。
萤火虫A受亮度较高的萤火虫B吸引而向B移动,A移动后的位置由下式决定:
CAi=CAi+β(CBi-CAi)+α(rand-(0.5))
(13)
式中,α为步长因子,α∈[0,1];rand是由3个随机因子构成的向量,在区间[0,1]上属于均匀分布。
FA-FCM组合聚类算法实现步骤如下:
(1)初始化FA算法参数β0,γ,α,c,T1,N(T1为FA算法最大迭代次数,N为萤火虫数)及萤火虫位置,设置FCM算法收敛阈值ε(ε>0)。
(2)将初始化的萤火虫位置作为初始聚类中心,联合式(7)、式(8)计算隶属度矩阵U(N×c)×(n)和距离d(vj,Ci),联合式(9)、(10)计算N只萤火虫亮度值矩阵Is(N×1)。
(3)比较各萤火虫亮度,联合式(11)、式(12)、式(13)更新各萤火虫位置。
(4)判断算法迭代次数是否达到T1,若是,则按式(7)~式(10)计算各萤火虫亮度,取最亮萤火虫位置为最优初始聚类中心;否则,返回步骤(2),继续迭代。
(5)确定初始聚类中心后,使用FCM聚类算法进行聚类分割,令FCM算法迭代次数t=0。

(7)按式(3)更新聚类中心位置,此时,t←t+1。
2.3 FA-FCM聚类有效性检验
为验证聚类方法的有效性,本文选取的评价指标为类内紧致度Var和类间离散度Sep[25]。
根据点云模型隶属度矩阵及聚类中心,类内紧致度为
式中,U为隶属度值Uij构成的隶属度矩阵,i=1,2,…,c,j=1,2,…,n;n(i)为第i个聚类中心样本数。
Var表示样本类内集中程度,Var越小,类内越紧致。
类间离散度为
0≤Sep(c,U)≤1
式中,FX、FY为两个模糊集合;vj表示样本点向量,j=1,2,…,n;min(UXj,UYj)表示该样本点分别属于FX和FY隶属度的最小值;S(FX,FY)表示两集合间相似度;当FX=FY时,Sep(c,U)=0。
Sep表示两聚类集群离散度,Sep越大,各类间越分散。
为综合评价聚类结果,将Var与Sep结合,定义综合评价指标为
VS越小,聚类效果越好。
3 特征点提取
3.1 边界点剔除与合并
应用FA-FCM聚类算法对点云模型进行分割后,需要对各分割块边界点进行特征点提取,在特征点提取过程中,所得分割块的边界点有两种情况需要处理。首先,过分割问题的存在容易致使模型平坦区域出现分割线,显然该分割线为非特征线,该分割线处的点为明显非特征点,表示该分割线的两组边界点相邻且共面,应从边界点集中剔除;其次,若分割线为特征线,则表示该分割线的两组边界点相邻但不共面,应对其进行合并处理。
本文在利用邻近投影点相邻向量夹角的方法[26]提取各分割块边界点的基础上,对边界点进行优化处理,剔除相邻且共面的边界点,合并相邻但不共面的边界点。
为直观表达,以图2所示圆柱体与长方体的组合模型为例进行说明。图2a所示为该组合模型经FA-FCM算法聚类分割后所得结果,由该图可知,为有效分割长方体四个侧面,圆柱体侧面也会被划分为四组,存在过分割现象,导致圆柱体侧面边界点集l1、m1为非特征点集,长方体相邻两侧面边界点集l2、m2均为两侧面交线处特征点,如图2b所示。为此,以各分割块为处理单元,通过分析比较两分割块边界点间距离和法向夹角,利用设置阈值的方法剔除相邻且共面的边界点集(如l1、m1),将相邻但不共面的边界点集(如l2、m2)合并,方法如下。

(a)区域聚类分割结果 (b)边界点提取结果图2 边界点优化准则Fig.2 Optimization rule of boundary points
模型分割后,定义分割块边界点集为
F={fi}i=1,2,…,c
式中,fi为第i个分割块边界点集。
给定任意两组边界点集fw1,fw2(w1,w2=1,2,…,c,w2≠w2),依据点云密度设置距离阈值D,以及依据边界点集fw1和fw2所对应分割块的聚类中心间夹角设置法向夹角阈值T,分别取fw1和fw2中任一点su1(u1=1,2,…,n1)和su2(u2=1,2,…,n2),n1、n2为各点集总点数,求su1、su2两点间坐标距离d、法向夹角φ。判定准则如下:
(1)若d≥D,则点su1、su2不做任何处理。
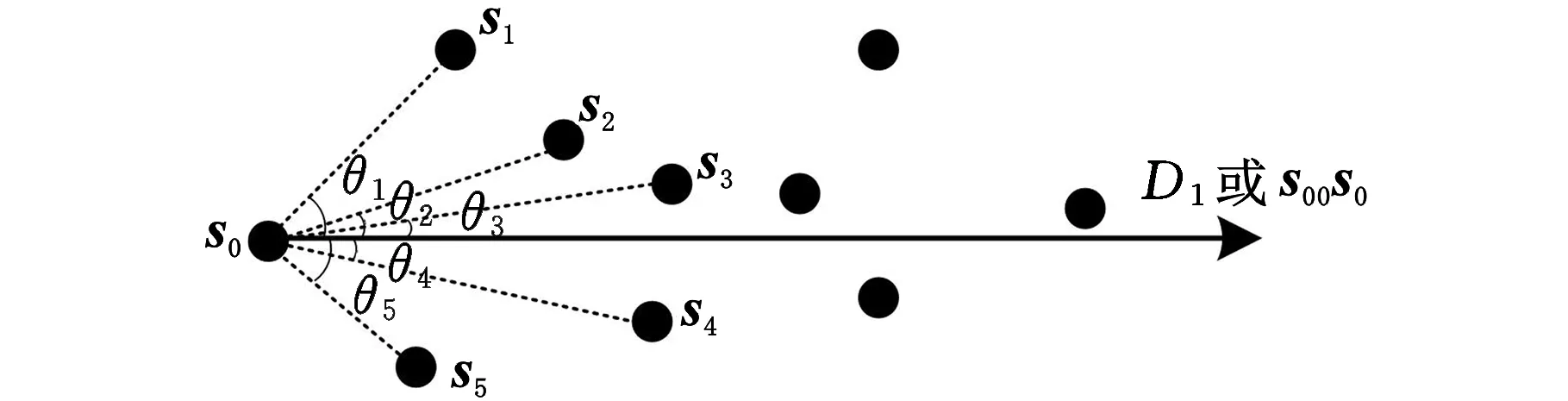
(2)若d (3)若d 各分割块边界点集经优化处理后所得点集为无序点,称该无序状态点集为候选特征点集,为便于曲线拟合,需先对候选特征点进行排序,然后再拟合成线。然而,由于点云数据在获取过程中不可避免地受外界环境、扫描设备等因素影响,导致候选特征点集中存在噪点,若直接对排序后的候选特征点进行曲线拟合,则噪点的存在会严重影响拟合精度,因此,以各点局部邻域主轴方向[27]为基准对排序后的候选特征点进行平滑处理。 取排序后候选特征点集中的一点s0,确定点s0的邻域值k0,对于邻域内任意点su(u=1,2,…,k0),记s0与su两点连线方向s0su与平滑参考方向正向夹角为θu(u=1,2,…,k0),如图3b所示。平滑参考方向构造法如下: (1)候选特征点s0为初始点时,无参考方向,取局部邻域点PCA主轴方向D1为平滑参考方向,如图3a所示。 (a)采样点局部邻域点集及主轴方向 (b)相邻点方向夹角图3 候选特征点平滑准则Fig.3 Smoothing rule of candidate feature points (2)候选特征点s0为非初始点时,取s0的前一点s00与s0的连线方向s00s0为平滑参考方向。 确定参考方向后,平滑准则如下: (1)距离准则。min(|s0su|)(|s0su|表示点s0与点su的距离,u=1,2,…,k0),即查找k0邻域内距s0最近的点。 (2)夹角准则。min(θu)(u=1,2,…,k0),即查找s0和k0邻域内任意点su(u=1,2,…,k0)的连线方向s0su与平滑参考方向正向间夹角最小的点。 如图3b所示,取邻域值k0为5,搜索s0的下一点,min(|s0su|)=|s0s5|,min(θu)=θ3。仅使用距离准则时,s5被确定为s0的下一点,此时s5与平滑参考方向角度偏差太大;仅使用夹角准则时,s3被确定为s0的下一点,此时距离跨度太长,直线拐点处特征点不易保留,容易出现过度平滑现象。因此,在对候选特征点进行平滑处理的过程中,应组合使用距离准则和夹角准则,设置夹角阈值T2,对满足条件θu 根据候选特征点分布特性设置夹角阈值T2,多次调整阈值以达到最佳平滑效果,在实验过程中,对直线和曲线类特征线设置不同的角度阈值T2,分别为T2=5°~10°和T2=20°~30°。 本文将基于法向量的FA-FCM聚类算法应用于点云模型特征线提取问题中,选取AIM@SHAHE Shape Repository公开数据库中的Smooth、Fandisk、Vase模型以及Princeton ModelelNet数据库中的m932-table模型作为实验对象,验证所提算法的可行性和优越性。 目前萤火虫算法的参数设置还没有明确合理的参考值,为此,首先通过分析比较文献中的参数值来设置合理的参数范围,然后测试不同的参数组合,确定该特征线提取算法的初始化参数值,设置见表1。 表1 参数列表Tab.1 The list of parameters 为验证本文算法的可行性,选取Smooth、Fandisk、Table和Vase模型进行特征线提取。首先估算各模型数据点法向,由FA-FCM混合算法对其进行聚类分割,各模型聚类有效性评价指标见表2。由表2可知,4个模型的Sep(0≤Sep≤1)值均接近于1,表明各模型整体划分效果较好,但分析比较Var值与VS值可知,Vase模型所对应的Var和VS值均为最大,表明Vase模型的聚类效果较差,还需进一步优化。 表2 各模型聚类有效性指标Tab.2 Cluster validity indexes of each model 4个模型经FA-FCM算法聚类分割后,基于各分割块边界点提取特征点,对应该相交的特征线端点进行合并处理,然后拟合生成特征线,各模型特征线提取不同阶段效果显示如图4~图7所示。 (a)Smooth模型原始点云 (b)区域聚类结果 (c)特征点提取结果 (d)特征线提取结果图4 Smooth模型特征线提取Fig.4 Feature line extraction from Smooth model (a)Fandisk模型原始点云 (b)区域聚类结果 (c)特征线提取结果图5 Fandisk模型特征线提取Fig.5 Feature line extraction from Fandisk model Smooth模型结构简单,主要由平面和曲面构成。图4b是模型经FA-FCM区域聚类分割所得结果,通过相邻两分割块交线提取该模型特征线,特征线以直线为主,特征信息较为突出,即为尖锐特征,图4c为Smooth模型特征点识别结果,表明模型尖锐特征点能够得到准确提取。 (a)Table模型原始点云 (b)区域聚类结果 (c)特征线提取结果图6 Table模型特征线提取Fig.6 Feature line extraction from Table model (a)Vase模型原始点云 (b)区域聚类结果 (c)特征线提取结果图7 Vase模型特征线提取Fig.7 Feature line extraction from the Vase model 图5为Fandisk模型特征线提取不同阶段效果图。Fandisk模型为机械轮盘模型,相比于Smooth模型结构较为复杂,既包含明显棱线(即尖锐特征线),又包含过渡特征线(如在模型底部相邻曲面相交处的特征点曲率变化较小,法向量方向相近,特征信息不明显,这类特征即为过渡特征)。图5c为Fandisk模型特征点识别结果,表明Fandisk模型的尖锐特征得到了完整提取,同时也有效保留了过渡特征。 图6为Table模型特征线提取不同阶段效果图。Table模型为餐桌模型,结构相对复杂,主要由平面、曲面以及球面构成,特征信息丰富,既包含尖锐特征,也包含细节特征,如模型桌脚及两球面相交处均包含有细节特征。图6c所示为Table模型特征点识别结果,表明本文所提方法在完整提取Table模型尖锐特征的同时也能有效识别模型细节特征。 图7为Vase模型特征线提取不同阶段效果图。Vase模型为构造复杂的花瓶模型,由内外两层曲面构成,特征线呈“之”字形,主要包括尖锐特征和过渡特征。与Fandisk模型相比,该模型曲面弯曲度较大,过渡特征的特征强度较弱且分布不均。图7c所示为Vase模型特征点识别结果,表明该算法对Vase模型中强度较弱的过渡特征提取效果不佳,部分特征线断裂。这与由表2得出的Vase模型聚类效果较差的结论相对应。 为对本文算法的特征线提取结果进行定量评价,分别计算各模型特征线的数量提取率和长度提取率。 模型数量提取率通过计算精确率Rpc和召回率Rrc[28]获得,精确率表示被正确提取的特征线数目占被提取出特征线总数的比值,召回率表示被正确提取的特征线数目占模型特征线总数的比值。精确率、召回率的计算公式如下: 式中,Tp为被正确提取的特征线数目;Fp为被错误提取的特征线数目;Tz为模型特征线总数。 模型长度提取率通过计算模型中各特征线段长度提取率的平均值获得,模型中某一特征线的长度提取率为已提取出的该特征线长度与其准确长度的比值。因为三维点云模型中特征曲线的准确长度不易求取,故本文利用“化曲为直”的思想,近似估算曲线长度。模型整体特征线长度提取率的计算公式如下: 式中,hq为第q条特征线的长度提取率(q=1,2,…,Tz);lq为已提取的该特征线长度;Lq为该特征线准确长度;H为模型整体特征线长度提取率。 对4种模型的精确率、召回率和模型长度提取率H进行统计,结果如表3所示。分析表3可知,Smooth模型和Fandisk模型的特征线提取结果更加完整和准确,所提取特征线不存在误判和漏判现象,由精确率、召回率及长度提取率H可判定Smooth和Fandisk的特征线基本得到了准确完整的提取,经细微调整后可投入实际应用中。Table模型特征线提取准确性较好,不存在误判现象,但由其Rrc值可判定该模型特征线未得到完整提取。此外,4种模型相比之下,Vase模型特征线提取的完整性和准确性较低,由其Rpc值和Rrc值可判定该模型的特征线提取既存在误判现象又存在漏判现象。但Table模型和Vase模型的召回率Rrc均达到90%,两模型长度提取率H均可达85%,表明本文方法在进行相对复杂模型的特征线提取时也可取得较好成效,可进行局部二次特征提取,从而有效识别强度信息不明显的特征点,提高模型特征线提取的完整性和准确性。 表3 各模型特征线数量提取率和长度提取率Tab.3 The extraction rate of the number and the length of feature lines of each model % 为进一步验证算法的可行性及优越性,选择Fandisk模型特征线提取结果与文献[29]提取结果进行对比,结果如图8所示。选择Vase模型特征线提取结果与文献[29]、[30]和[31]的提取结果进行对比,结果如图9所示。 (a)本文方法特征线提取(b)文献[29]特征线提取图8 Fandisk模型特征线提取方法对比Fig.8 Comparison of the feature extraction methods used in Fandisk model 在图8中,对比长方形框标定区域可以看出,文献[29]的方法不易识别特征强度逐渐减弱的平滑过渡区特征,从而导致特征线提取不完整,而本文方法所提取特征线的完整度以及线条光滑度相对较好。 由图9可知,本文算法能较好地识别内外两层特征线,两层线间不存在相互扭曲现象,曲线线条性更好,但不能完整识别特征强度较弱的特征点,致使曲线出现断裂和不完整现象。 (a)本文方法特征线提取 (b)文献[29]方法特征线提取 (c)文献[30]方法特征线提取 (d)文献[31]方法特征线提取 本文基于自适应邻域的FA-FCM算法实现点云模型的有效分割,通过构造边界点集剔除与合并准则以及候选特征点集平滑准则从各分割块边界点集中识别特征点。结合实验分析得出以下结论: (1)相对于固定阈值的主成分分析(PCA)法,自适应邻域的PCA法可较为精准地估计模型尖锐特征点处法向,再通过荧火虫算法优化后的FCM算法可使模型分割效果达到最佳,从而提高各分割区边界点中特征点比率。 (2)边界点集剔除与合并准则可有效去除边界点集中多数非特征点,从而提高算法效率;同时,结合候选特征点集平滑准则的应用可使所提算法能够识别更多准确的模型特征,提高所拟合特征线的光滑度。 (3)通过4种实验模型的特征线提取精度分析可知,Smooth模型和Fandisk模型的特征线可得到准确完整的提取,结构相对复杂的Table模型和Vase模型特征线的数量提取率可达90%,长度提取率也可达85%,其中,主要特征线均可得到完整提取。结果表明,本文算法简单有效且具有一定的通用性,在准确提取点云模型显著特征和细节特征的同时能尽可能多地保留模型过渡特征。3.2 候选特征点平滑

4 实验结果与分析
4.1 主要参数设置

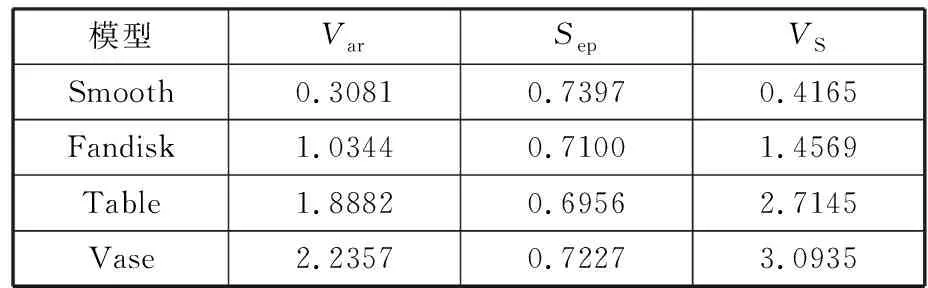
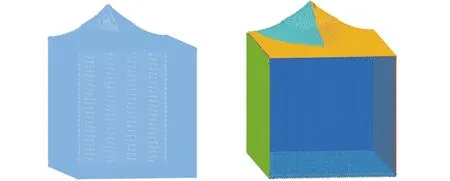
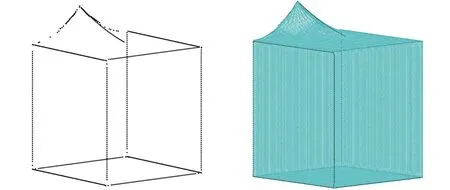
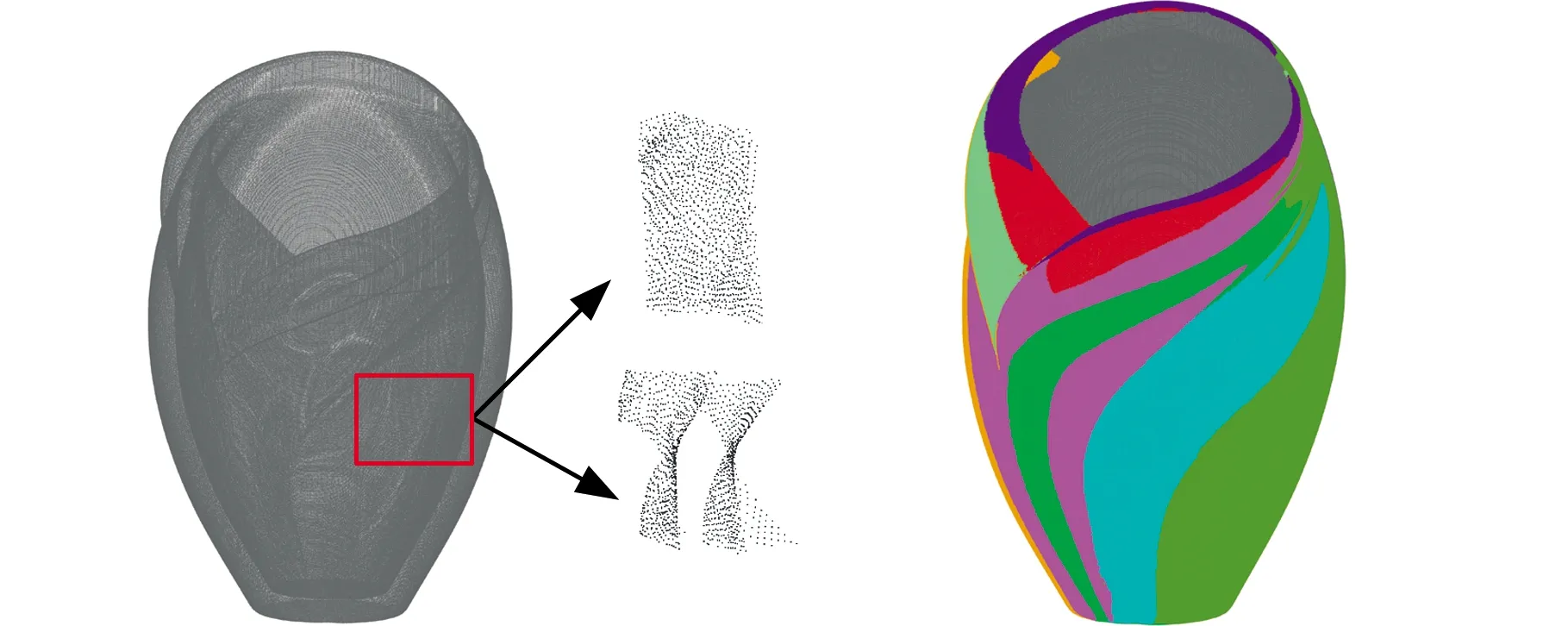
4.2 特征线提取结果的有效性及精度分析




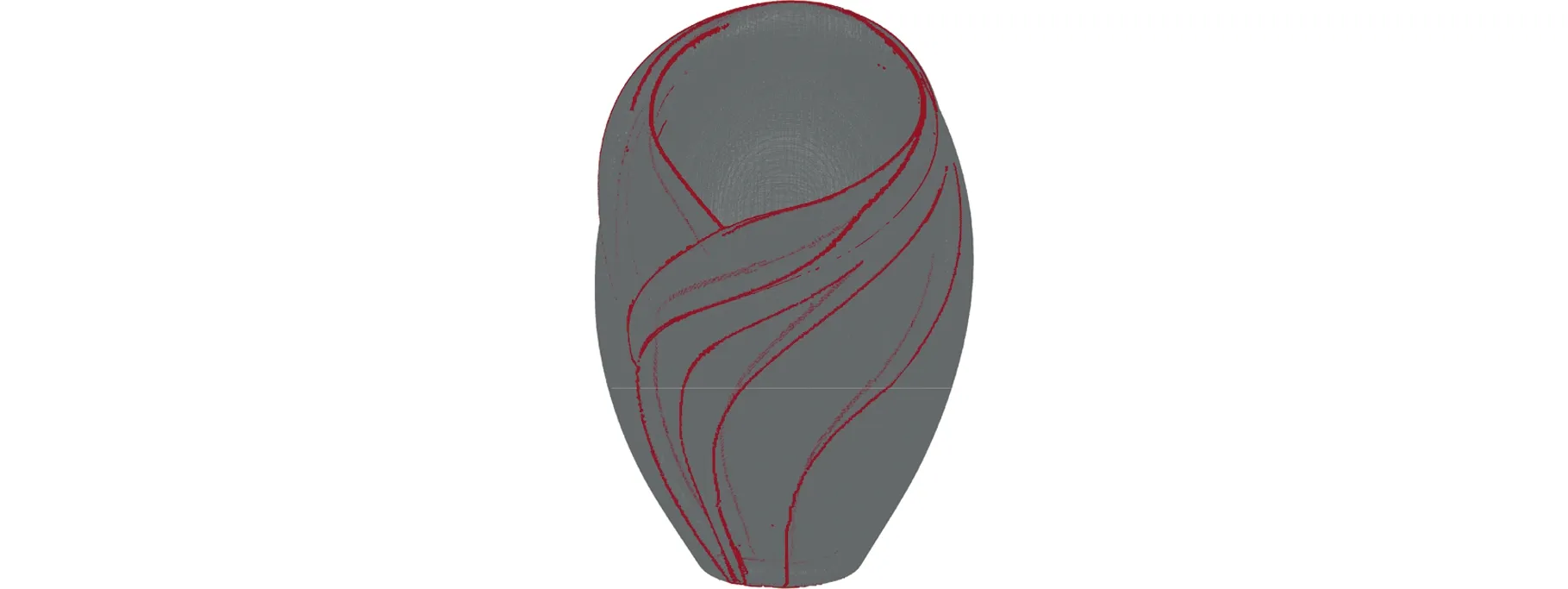

4.3 特征线提取方法对比
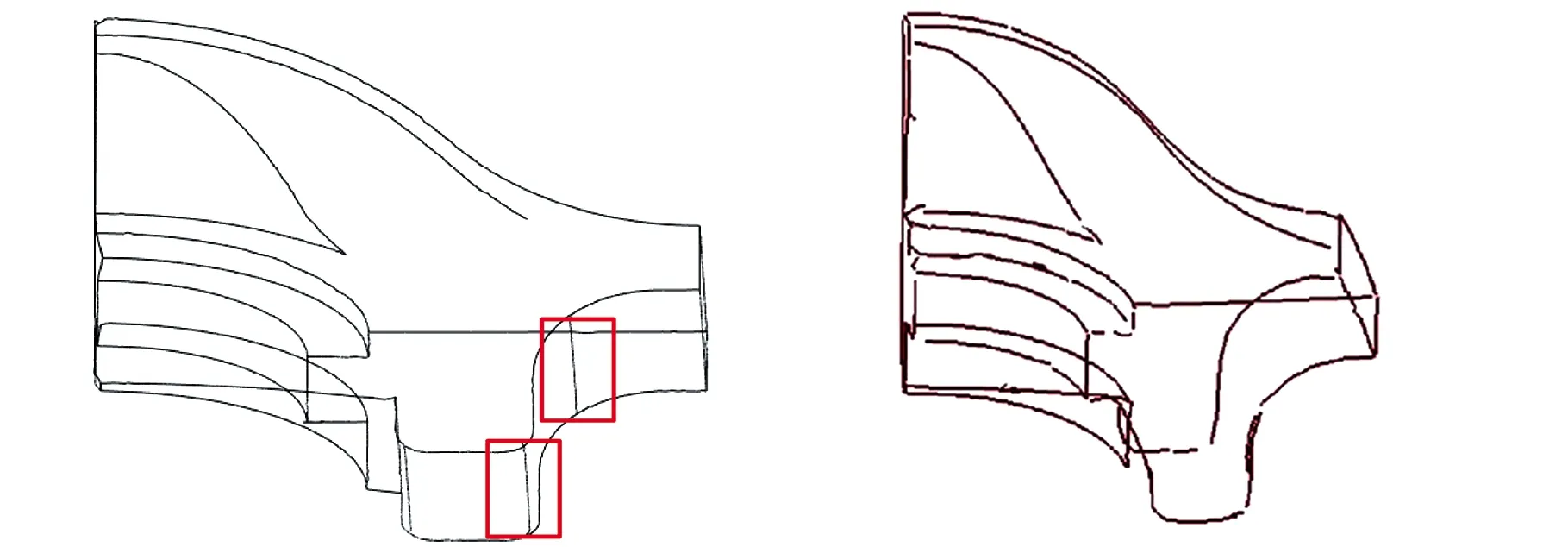
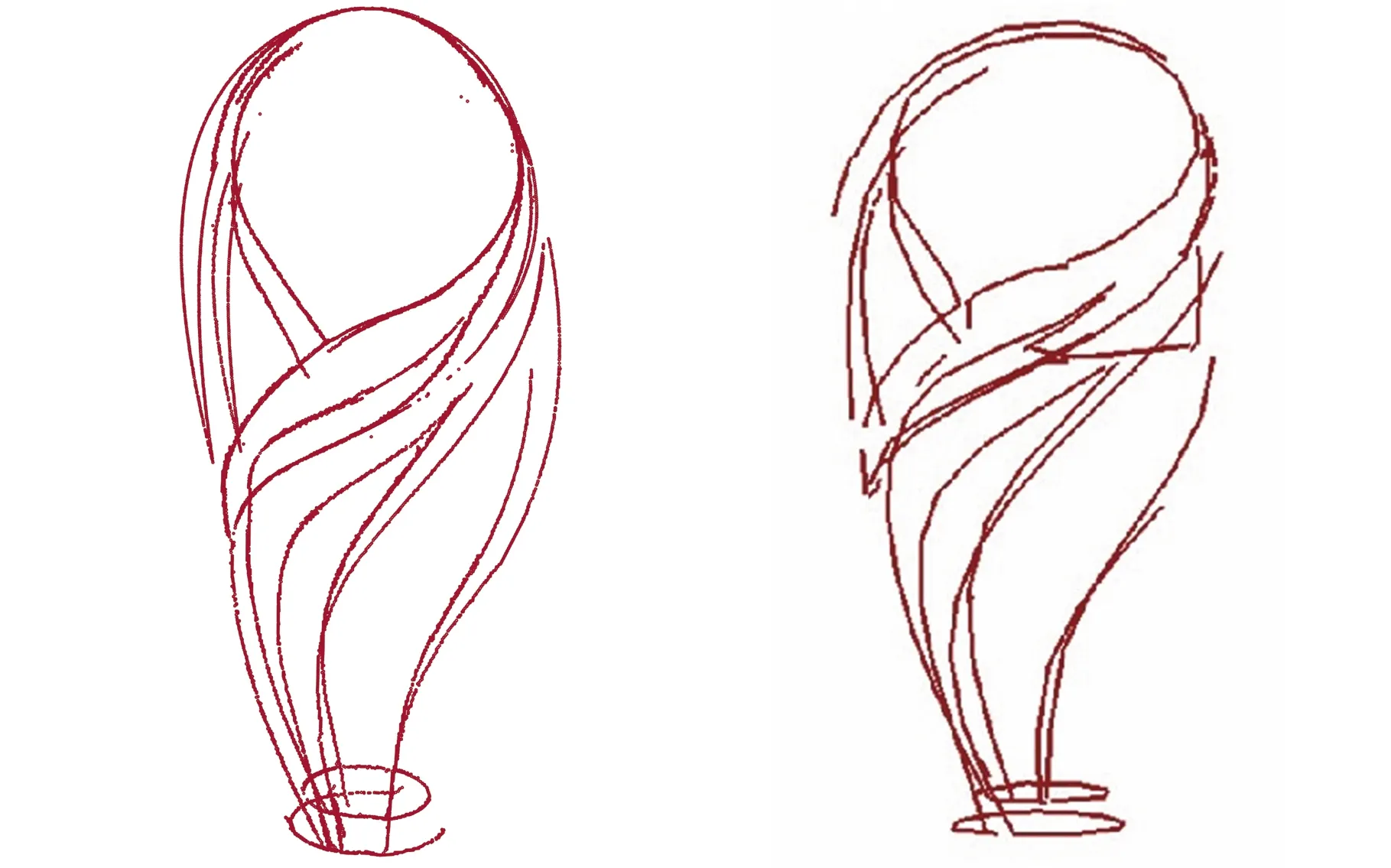

5 结论

