基于MATLAB/Simulink动力换档变速箱换挡过程仿真研究*

刘彩霞 尹 明

(1.包头职业技术学院 数控技术系，内蒙古 包头 014030；2.内蒙古科技大学 机械工程学院，内蒙古 包头014010)

在国内外的许多汽车、工程车辆都装了行星变速箱，行星变速箱包括换挡制动器、换挡离合器和具有行星齿轮的变速机构等[1]。行星齿轮变速箱最重要的优点是改善了换档的平顺性、驾驶的平稳性及乘坐的舒适性。开始换挡时主、被动摩擦片会产生滑动，随着换挡进行，操纵油压上升，摩擦力矩增大，最终使得被动轴转速等于主动轴的转速，接合结束，所以说是一个动态变化的换挡过程。而在换挡时如何找到最佳的参数来满足换档的平顺性、平稳性及舒适性。根据相关资料及实验数据，当主、被动盘的接合转速在10左右，接合时间是2.4s，被动盘的加速度在2.5倍的重力加速度(6m/s2)范围内时，能体现换挡平稳性好、冲击度小[2]。国内外学者主要是研究换挡时运动数学模型的建立，而对满足换挡性能的换挡参数的研究较少，作者通过应用MATLAB/Simulink模拟找出适合换挡的较佳油压上升时间、上升速度、油压规律及滑摩力矩。

1 运动数学模型的建立

1.1 用结构联系矩阵转换转速矩阵

动力换挡行星变速箱的内部结构通常用传动方案简图表示结构关系，如图1所示。通用的计算机是不能识别这种用传动方案简图的，需将其内部结构转换成能用计算机表示和存储的方法。

矩阵C用一个h×m维结构联系矩阵表示，其行对应于构件，列对应于运动件。则图1建立的结构联系矩阵如式(1-1)所示。

1-输入轴；2-输出轴；3、6-太阳轮；4、7-行星架；5、8-齿圈；9、10-制动器摩擦盘；11、12-离合器摩擦盘Ⅰ-构件Ⅰ；Ⅱ-构件Ⅱ；Ⅲ-构件Ⅲ；Ⅳ-构件Ⅳ图1 二自由度行星变速箱动力换挡传动简图

式(1-1)

结构联系矩阵C可变换为转速矩阵。式(1-2)表示转换后的转速矩阵。

式(1-2)

在图1中一档时运动件9、11、12不动作，而制动器摩擦盘10动作；二档时制动器摩擦盘9、10不动作，离合器摩擦盘11、12动作；倒档时运动件10、11、12不动作，制动器摩擦盘9动作。

1.2 二个自由度的动力换挡行星变速箱的运动微分方程的建立方法

1.2.1 非独立运动件转速表示方法

非独立运动件转速的转速可以用独立运动件转速表示，现设一个行星变速箱的自由度数是2，矩阵Bm的(m-l)个方程是线性无关的，当有m个运动件时，它的转速矩阵Bm为(m-2)×m阶矩阵[4]，初等变化后的Bm为：

式(1-3)

假设m和m-1是独立运动件，其转速为ωm和ωm-1，那么其他运动件的转速表示为：

……

式(1-4)

当11、12为独立运动件时,初等变换后的转速：

式(1-5)

现在非独立运动件转速为：

ω1=ω11,ω2=ω12,ΛΛ,ω10=-0.366ω11+1.37ω12

1.2.2 建立运动微分方程

式(1-6)

式中：mpi为行星轮质量,Jpi为转动惯量。

经变换后的运动微分方程为：

式(1-7)

1.2.3 广义力矩的确定及转换矩阵

广义力矩是指把动力换挡变速箱的外力矩通过转换矩阵等效折算到独立运动件上的力矩。变速箱外力矩一般包括：离合器摩擦力矩，制动器摩擦力矩，输入、输出力矩[4]。

外力矩对系统做的功为：

式(1-8)

式(1-9)

变形后行星变速箱运动微分方程为：

式(1-10)

式(1-10)建立的是行星变速箱换挡瞬时的运动数学模型，给出力矩值就能求解方程组，它描述了换档离合器接合过程转矩、转速的变化规律。

2 动力换挡行星变速箱换档离合器摩擦系数和滑摩力矩

式(1-11)所表示的运动微分方程中有外力矩，其中滑摩力矩对换挡离合器动态过程影响很大，故对离合器的滑摩力矩的计算非常重要。

2.1 摩擦片的动摩擦系数的推导

行星变速箱采用湿式多片离合器，包括主、被动摩擦片。随着压力、温度、滑动速度的变化摩擦系数也变化，经实验研究证明，动摩擦系数是随着滑动速度的增大而减少，其规律用指数曲线拟合最逼真。

假设

u(v)=aebv

式(2-1)

变换公式并用最小二乘法进行拟合，得出：

a=eA,b=B

式(2-2)

对一种常用的摩擦片进行试验，用测得数据拟合，得到的动摩擦系数为：

u=aebv=0.113e-0.0558v

2.2 滑摩力矩的计算

滑摩力矩是摩擦片被操纵油缸压紧后，主、被动摩擦片间产生相对滑动的结果。滑摩力矩随内外径尺寸而变化。设操纵油压从零上升到额定压力的时间为，其随时间变化成线性增长规律[5]。

将拟合的滑摩系数u(Δwr)=aebΔωr带入式(2-3)，得出离合器总摩擦力矩：

式(2-3)

式中，z—摩擦副数，r—摩擦片半径，F(t)—离合器摩擦片上的压紧力。

3 行星变速箱换挡过程的仿真与分析

3.1 动力换挡变速箱的模拟仿真

以ZL-50轮式装载机的行星变速箱仿真，已知：输入转矩Ml=729Nm，输入速度ω1=16.1r/s，输出阻力矩M2=689Nm，输出速度ω2=5.2r/s。当Ⅰ档换到Ⅱ档时，制动器松开，离合器接合，操纵油压按线性规律上升[2]。

表1 离合器结构尺寸 mm

表2 各构件转动惯量 kg·mm2

以给定油压的上升规律得出滑摩力矩来仿真行星变速箱换挡过程。如果用前面推导公式进行换挡过程的仿真是非常困难的，现将油压上升规律和滑摩力矩公式进行简化，然后使用MATLAB/Simulink模块对换挡过程进行模拟仿真，找出符合车辆换挡接合转速在10r/s左右，接合时间在2.4s之内，被动盘角加速度在2.5倍的重力加速度6m/s2范围内的油压上升规律的参数(T、K)值。其中用2.4s之内能反映换挡接合时间短、换挡快，6m/s2反映换挡的平稳性好、可靠性高。

3.2 仿真前期的数学处理

主被动盘11、12作为独立运动件，带入公式计算得出：

等效转动惯量的矩阵：

力矩转换矩阵：

得到运动微分方程组为：

式(3-1)

式中：Ml—滑摩力矩；Mo—输出阻转矩；Mi—输入转矩；后面两个零表示制动器没有动作。

可知油压规律为：

式(3-2)

式中，K—油压上升斜率，t—油压上升时间，T—是油压上升时间范围值，G—上升后的恒定值。

简化后Ml的公式如下：

式(3-3)

式中，R2，R1—摩擦片内外径尺寸；Rf1，Rf2—油缸内外径尺寸。将式(3-2)代入式(3-3)得：

式(3-4)

3.3 运用MATLAB/simulink建立仿真模型

如图2所示，在MATLAB/simulink中建成的仿真模型。

图2 二自由度动力换挡变速箱仿真模型

其中M1的函数为：

function y =cal(u)

if u<0.4

y=137.5*u+6913.5;

else

y=7463.5;

end

运动微分方程的其它函数为：

function y =fcn(u)

d=[0.2016 -0.0024;-0.0024 29.8192];

e=[1 0 -1 0 0;0 -1 1 0 0];

f=[729;689;u(1);0;0];

y=inv(d)*e*f;

3.4 仿真结果分析

下面分析仿真结果，仿真时保证式(3-4)中b和c不变，试验a，即K值变化使a值变化得到主被盘转速的变化过程。列出两组数据的仿真曲线。

当T=0.4s

K=50000

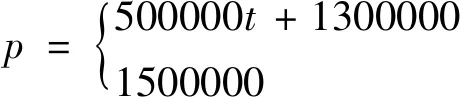
仿真如图3所示。

图3(a)换挡离合器的ω11、ω12曲线图

图3(b)被动盘12加速度曲线图

当T=2.6s

K=7692.308

仿真如图4所示。

图4(a)换挡离合器的ω11、ω12曲线图

图4(b)被动盘12加速度曲线图

当K值从100000按一定规律逐渐减小到7692.3077。给定9组数据仿真，当油压的初始值和最大值给定且压差保持在200000Pa，油压上升速度K逐渐减小，油压上升时间T逐渐增加时，其换挡速度保持在12r/s和13r/s数值上，而主、被动摩擦盘11、12的接合时间由1.4s增加到2.4s，换挡速度和时间基本满足换挡接合要求的速度和时间。被动盘12的加速度上升时间由0.2s延长到2.6s，且最大值在9m/s2以上，这个值超过了2.5倍的重力加速度6 m/s2范，使得换挡的冲击度大，不能满足换挡平顺性、舒适性的要求，且影响换挡元件的使用寿命，说明给定P,Ml的值不符合实际的要求。

T=2.6s

K=7692.308不变

油压的压差值为200000Pa

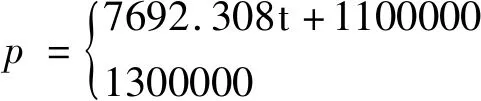
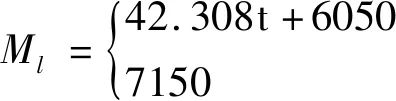
通过仿真发现ω11从初始值往上升，和ω12不会有交点，而被动盘加速度的斜率比较大，加速度的最大值在减小，说明初始值和最大值减小得大了，现将油压初始值增加为1160909.09 Pa，摩擦转矩的初始值为6379Nm ，如图6所示的仿真结果。此时运动件12的加速度在6m/s2内，满足了换挡加速度的要求。运动件11、12约在5s时速度相等，动力换挡离合器的换挡接合时间过长，不符合实际的需要。

图5(a)换挡离合器的ω11、ω12曲线图

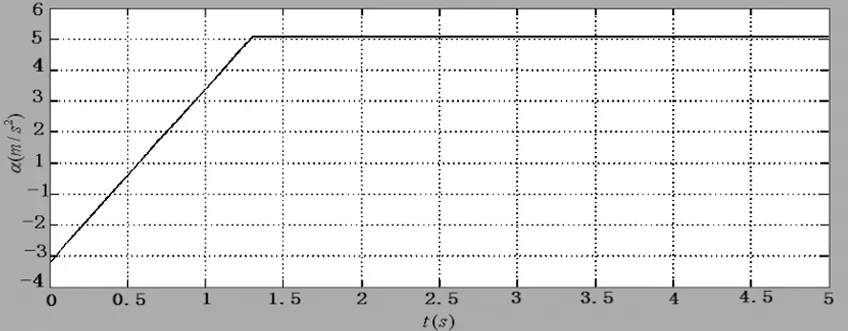
图5(b)被动盘12加速度曲线图

将油压的初始值减小为1156366.37Pa，摩擦转矩的初始值为6360Nm仿真结果如图7所示。运动件12的加速度已在6m/s2的范围内，满足2.5倍的重力加速度的要求，但是换挡接合时间为4.6s，这不符合2.4s的要求。结合前面仿真数据，减小T值和K值。

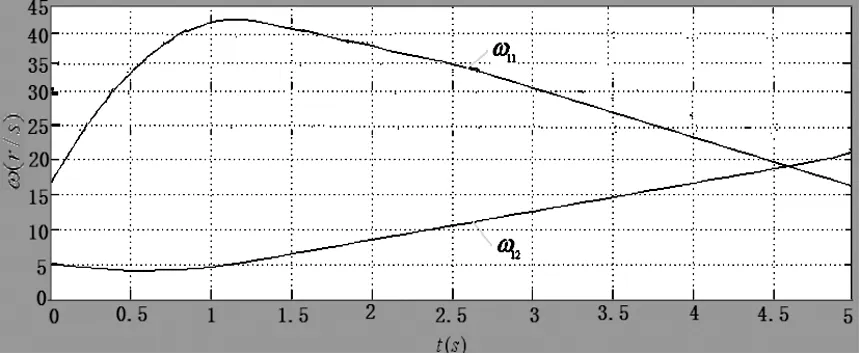
图6(a)换挡离合器的ω11、ω12曲线图

图6(b)被动盘12加速度曲线图

现T=0.4s

K=50000

油压的初始值和最大值根据实际取1157000Pa和1357000Pa

图7(a)换挡离合器的ω11、ω12曲线图

图7(b)被动盘12加速度曲线图

通过上面一系列的仿真看出图7曲线更好些，图中主、被盘接合速度约为，接合时间是2.4s，被动盘的加速度约是5.8m/s2，这和一些实验证明的数值相吻合。体现换挡平稳性好、冲击度小。已满足理想的主被动盘的接合角速度约在10r/s，接合时间是2.4s，被动盘的加速度是6 m/s2，仿真值已在这些值范围内，说明这一组仿真曲线是较理想的曲线，得到这一组曲线所给的参数值是：

T=0.4s

K=50000

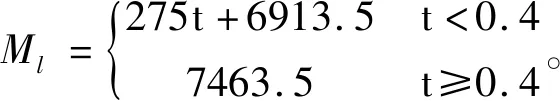
4 结语

本文研究的是行星变速箱换档离合器的运动数学模型建立和换挡瞬时过程随油压变化规律引起换挡品质评价指标的仿真过程，应用所建立的运动微分方程及摩擦力矩,推导出油压变化规律影响摩擦力矩，摩擦力矩对车辆的平稳性有很大的影响。行星变速箱换挡主要是由操作油缸产生压紧力实现的，从仿真的过程得出，液压油的上升时间T和上升速度K主要影响换挡速度和时间，当K减小时、换挡速度减小、换挡接合时间增加，而油压的初始值、最大值、压差值将影响换挡冲击度、平顺性和换挡元件的寿命，油压初始值、最大值设定的大，被动盘的加速度将增加、换挡冲击度大、换挡的平顺性不好，所以在设计换挡离合器时应合理选择液压油的上升时间、上升速度、初始值、最大值和压差值。通过仿真得出满足换挡品质评价指标最佳的油压上升时间T、油压上升速度K、油压规律值和摩擦转矩值。