确定性系数模型的滑坡易发性评价应用与比较*

宋小川，刘汉湖，张 春，周林博

(成都理工大学 地球科学学院，四川 成都 610051)

滑坡是常见地质灾害之一，容易造成大量生命财产损失和生态环境破坏。我国滑坡地质灾害频发，因此，需要对滑坡地质灾害有全面的认识，为此进行滑坡灾害易发性评价就显得尤为重要。

国内外许多学者在研究滑坡易发性中，先后提出了多种评价方法，滑坡易发性评价从最开始的定性分析(如：专家打分法、层次分析法[1-3]、加权线性组合法[4]等)，如许冲等人利用层次分析法对汶川地震区的滑坡易发性评价[5]，层次分析法作为一种多因素分析方法，有一定的主观因素影响，基于专家知识逐一对比每两个影响因子之间的关系，使易发性评级结果较为主观，受人为因素的影响较大；再到被科学界认为更客观、更适合用于滑坡易发性评价的统计学方法，可以大限度减少专家的主观性，应用比较广泛的统计预测模型有[6-9]逻辑回归、信息量、确定性系数等。随着机器学习与人工智能的不断发展，机器学习模型[10-12](BP神经网络、随机森林、支持向量机等)也得到极为广泛的应用。对比以上方法，定性分析方法受主观因素影响较大，机器学习在精度上具有一定的优势，但以此为基础的评价模型过程复杂，而统计学方法原理容易理解、操作更易于实现，在更新评价指标时只需将指标的统计系数叠加到原始评价结果中，不需再对整个研究区进行重新评价，具有较好的推广和应用价值。

综上，选取了统计预测模型中应用比较广泛的信息量与确定性系数模型用于该区域的滑坡易发性评价，希望能为滑坡易发性评价提供一定的理论与依据。

1 研究区与研究方法

1.1 研究区概况

雷波县位于四川省西南边缘、金沙江下游北岸，属凉山彝族自治州所辖，地理坐标为东经103°10′～103°52′，北纬27°49′～28°36′，如图1所示，全县幅员面积2 932 km2，海拔277.6～4 067 m，属于金沙江高中山峡谷气候，干湿季节分布明显，年降雨量主要集中于夏、秋两季，年气温差异较小，地方气候特点比较突出，受诸多因素影响，区内气候变化明显，县域内构造带也较为发育。以上的地质地貌条件，孕育了雷波县滑坡灾害发生的自然环境。

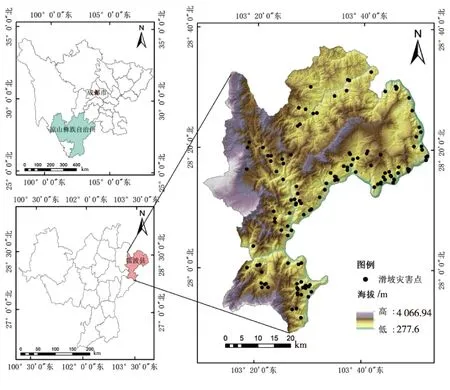
图1 研究区地理位置图

1.2 数据来源

本次数据包括：空间分辨率为10 m的数字高程模型(DEM)，1：100 000地质图(图幅号为H48D011003、H48D011004、H48D012003、H48D012004、G48D001003、G48D001004)，河流与路网数据来源于全国地理信息资源目录服务系统(https://www.webmap.cn/)，地理空间数据云(http://www.gscloud.cn/)下载的空间分辨率为30 m的Landsat8遥感影像，野外地质灾害调查资料收集的滑坡点数据129处。

2 滑坡易发性评价方法与因子选取

2.1 研究方法

2.1.1 信息量模型

导致滑坡灾害发生的因素较多，信息量模型是通过计算滑坡发生的密度来表征各影响因子分级下滑坡发生的信息量大小，再通过叠加各因子分级下的信息量值，完成滑坡易发性分区[13-14]，其原理公式如下：

(1)

式中，I(y，x1，x2，…，xn)为因子组合x1，x2，…，xn对滑坡灾害提供的信息量；P(y，x1，x2，…，xn)为因子组合x1，x2，…，xn条件下滑坡灾害发生的概率；P(y)为滑坡灾害发生概率。

在实际运用过程中，一般采用以下模型计算：

(1)首先，计算单因子x对滑坡灾害(D)发生提供的信息量I(xi，D)：

(2)

(2)计算单个评价单元中总的信息量值：

(3)

式中，Ni为某一因子分级xi中发生滑坡的个数；Si为xi的栅格总数；N为研究区内滑坡总数；S为研究区总栅格数；I为评价单元总的信息量。

2.1.2 确定性系数

确定性系数(Certainty Factor，CF)是一个概率统计指标，此指标通过已经发生的滑坡灾害与确定影响灾害发生的若干因子之间的统计关系，来分析各影响因子敏感性[15]。其表达式如下：

(4)

式中，PPa为滑坡灾害在某一影响因子分级a中发生的概率，即是分级a中滑坡灾害数量(或面积)与分级单元数量(或面积)的比值；PPs为滑坡灾害在整个研究区发生的概率，是整个研究区滑坡灾害数量(或面积)与研究区单元数量(或面积)的比值。CF取值范围在[-1，1]，其值越大，表示发生滑坡灾害的概率越大。

2.1.3 精度验证

利用测试数据集，采用统计方法和受试者工作特征(Receiver Operating Characteristic，ROC)曲线对滑坡模型的性能进行评价。使用的统计方法是精确率(precision)、召回率(recall)、准确率(accuracy)和ROC曲线[16]。

(5)

(6)

(7)

式中， FP为误分类滑坡的数量样本；FN为误分类的非滑坡样本数量；TP为正确分类的滑坡样本数量；TN为正确分类的非滑坡样本数量。如表1所示。

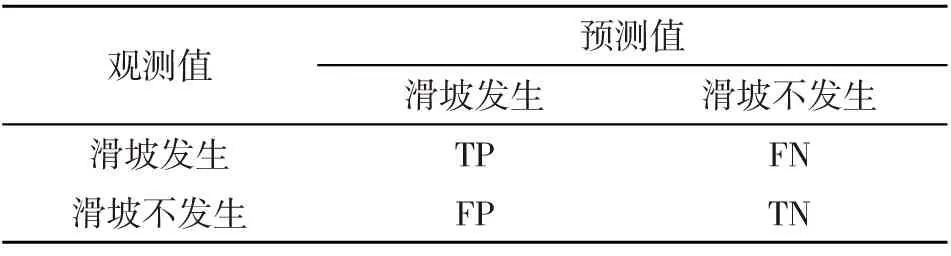
表1 混淆矩阵

2.2 评价单元与因子选取分级

首先，需要选取规则的评价单元，所用数字高程模型分辨率为10 m，因此，将单元格划分为10 m×10 m大小，通过ArcGIS重采样功能将各个因子图层转化为10 m×10 m大小的栅格，同时，所有因子图层采用统一坐标系(CGCS2000)。

评价因子的选取数量对于评价分析也尤为关键，在结合滑坡影响因素以及资料收集的前提下，主要考虑了地理环境因子、地质环境因子、人类活动因子三个方面。选取坡度、坡向、高程、归一化植被指数、距河流距离为地理环境因子；选取距断层距离、地层岩性为地质环境因子；选取距道路距离为人类活动因子。

将坡向按照方向进行分级。将高程、坡度、归一化植被指数按照自然间断法进行分级。自然间断法是一种依据数值统计分布规律分级和分类的统计方法，它能使类与类之间的不同最大化。将距道路、河流距离以500 m为步长进行分级，距断层距离以800 m为步长进行分级。针对岩土体的整体性及复杂性，将岩组划分为5类，分别为碎屑岩软质～半坚硬，碳酸盐岩硬质岩组，玄武岩坚硬岩组，砂、泥岩软质～半坚硬，第四系松散碎石、粘土。

2.2.1 地理环境因子

(1)高程

滑坡灾害的发生受海拔高度的影响，不同的海拔范围影响强度也不同。研究区最高4 067 m，最低277 m，高差较大，不同高程对该区域的滑坡灾害发生影响程度也不同，采用ArcGIS自然间断法进行分级，如图2(a)所示。

(2)坡度

不同坡度对滑坡灾害发生的影响也具有差异，通过DEM数据，利用ArcGIS空间分析功能，采用自然间断法分为5类，如图2(b)所示。

(3)坡向

不同坡向的光照强度影响着植被覆盖、斜坡体稳定性等。研究区坡向为-1°～360°。根据其方向分为10类，如图2(c)所示。

(4)归一化植被指数

归一化植被指数是植被覆盖密度的评价指标，植被覆盖好的区域不利于灾害的发生。采用自然间断法将其分为5级，如图2(d)所示。

(5)距河流距离

距河流的远近影响着斜坡的稳定性，距离越近其影响越大。研究区均属长江上游金沙江水系，区内金沙江由南西向北东向穿过，采用ArcGIS欧氏距离以500 m为间隔进行分级，如图2(e)所示。

2.2.2 地质环境因子

(1)距断层距离

断裂构造严重影响着滑坡灾害的发生，研究区不同方向构造带较为发育。利用ArcGIS欧氏距离分析，以800 m为间隔进行分级，如图2(f)所示。

(2)地层岩性

不同的地层岩性影响着斜坡岩层的稳定性，岩性越脆弱，其发生滑坡灾害的概率就越大，根据研究区地质资料，将岩性大致分为5类，如图2(g)所示。

2.2.3 人类活动因子

人类活动也是滑坡灾害发生的重要因素，距离道路的远近差异也会受到不同程度的影响。利用ArcGIS欧氏距离分析，以500 m为间隔进行分级，如图2(h)所示。

图2 滑坡易发性评价因子分级

3 易发性结果对比分析

3.1 易发性评价结果

根据统计各影响因子的不同分级，计算两种评价模型各影响因子不同分级下的信息量值和CF值，两种评价模型易发性分区结果如图3所示。通过对各因子图层进行叠加分析，得出研究区信息量值的范围为[-7，3]，信息量值越大表明该区域发生滑坡灾害的可能性也越大；对叠加得到的确定性系数值进行归一化处理，利用ArcGIS对总信息量值、确定性系数值进行重分类，采取自然间断法将研究区分为低、较低、中、较高、高易发区。

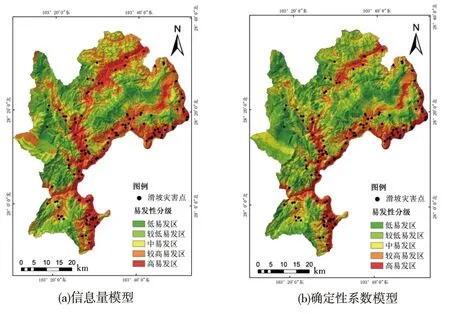
图3 滑坡易发性分区图

如表2所示，滑坡灾害主要集中在高程较低的区域，当高程大于1 800 m时滑坡比例仅占7%，而且信息量值与CF值均表现为负，说明大于1 800 m时滑坡易发性较小；坡向因子，除了在北方向上滑坡比例不超过5%，其他方向分布上较均匀，在10%～17%范围内，信息量值与CF值在东、南、西南、西方向上表现为正值；对于坡度因子，滑坡灾害点接近80%分布在36°以下，结合信息量值与CF值均表现为正值，可以看出坡度在36°以下更有利于滑坡灾害的发生；在植被覆盖度方面，结合信息量值与CF值，呈现负相关关系，表明植被覆盖越大越不利于滑坡灾害的发生；河流、断层、道路对于滑坡灾害的影响，表现为在一定距离范围内，距河流、断层、道路距离越近，其滑坡比例越大，表明其发生滑坡灾害的概率越大；在地层岩性方面，地层碎屑岩软质滑坡比例占60.47%，砂、泥岩软质滑坡比例占11.63%，有利于滑坡的发生，第四系松散碎石、粘土信息量值(1.108 512)、CF值(0.67)较大，也表明对滑坡发生影响程度较大，因为这几种地层岩性比较脆弱，容易发生地质灾害，这也与实际情况相符。

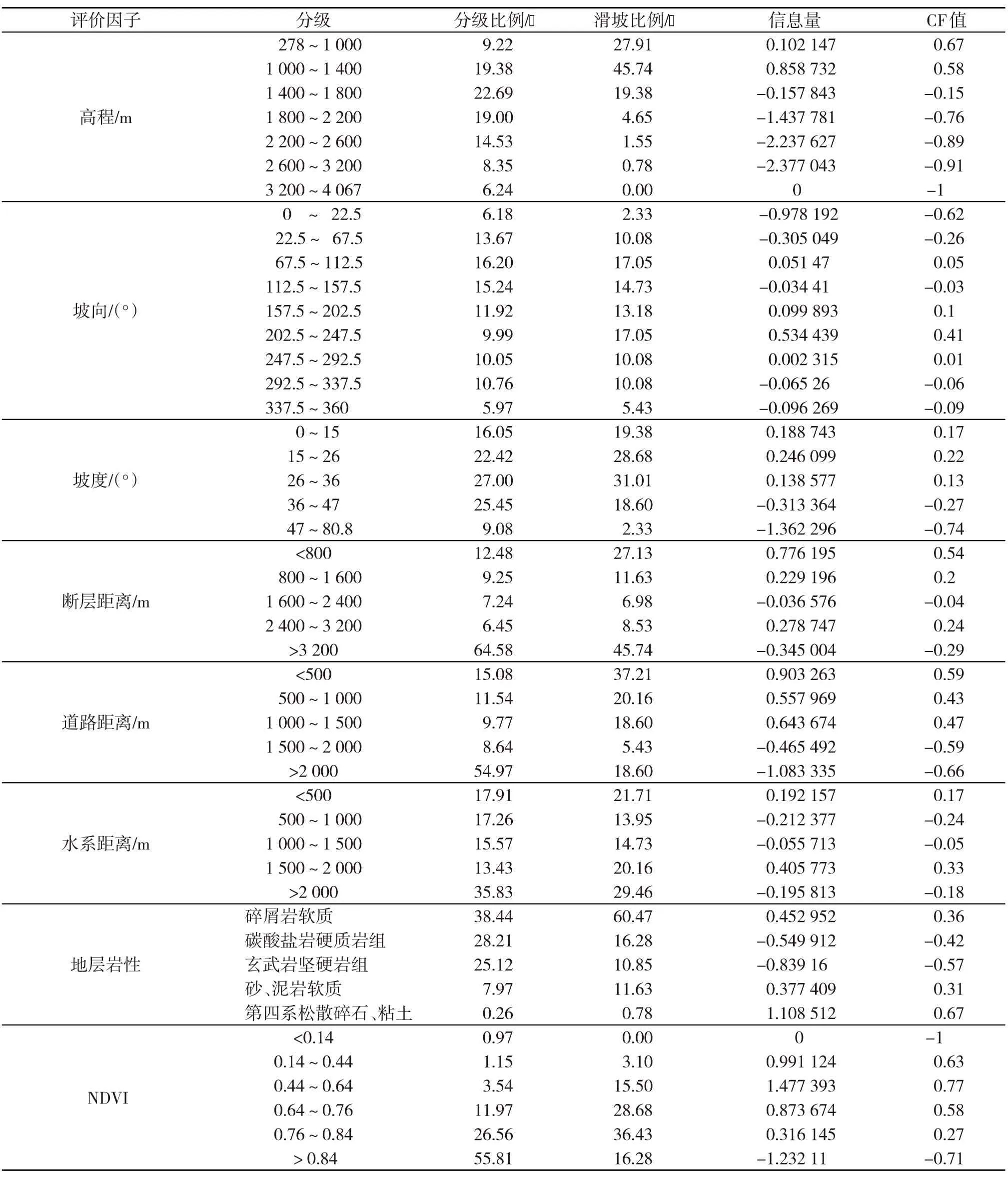
表2 滑坡易发性评价结果统计

3.2 易发性结果验证对比分析

通过选取滑坡点30%作为验证样本，并在已有滑坡点1 km内建立缓冲区，然后，在缓冲区外随机选取出相同数量的非滑坡点，将两者组成之后作为正负类样本，再利用ROC曲线分析两种模型对滑坡易发性评价的预测率。

如表3所示，信息量模型精确率(0.88)较高，但召回率(0.72)较低，确定性系数模型精确率0.81，召回率0.84，确定性系数模型准确预测的滑坡数量比例高于信息量模型。为了更好的评价模型的预测能力， 采用ROC曲线及曲线下面积(Area Under Curve，AUC)值对模型进行精度分析。ROC曲线以敏感性和特异性为垂直轴和水平轴，AUC值的大小用来评价模型的预测能力，值越接近1则表示模型预测能力越好，反之越差。

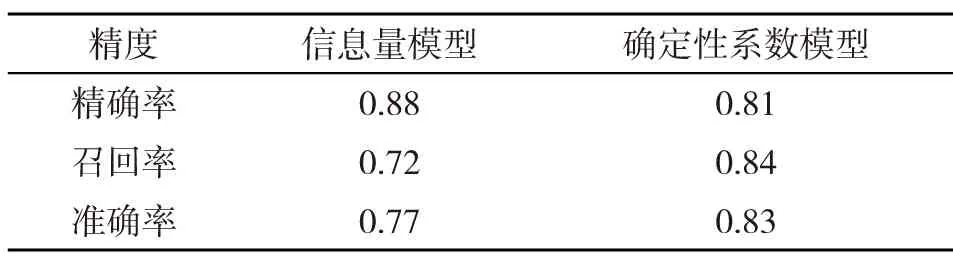
表3 不同模型的预测精度对比

如图4所示，信息量和确定性系数模型的AUC值分别是0.829 9、0.893 5，确定性系数模型AUC值大于信息量模型，说明确定性系数模型整体上预测效果更好。

图4 不同模型预测结果的ROC曲线

在面积分布上，如图5所示，两种模型均表现为以低、较低、中易发区为主，但在较高、高易发区分布面积上有一定差异，信息量模型分布面积占比41.85%，确定性系数模型分布面积占比27.42%；在滑坡数量上，信息量模型有81%的滑坡点位于较高和高易发区，而确定性系数模型有80%的滑坡点位于较高和高易发区。结合分区面积，前者较高、高易发区分布面积占比较大，而后者分布面积较小，分析可得出确定性系数模型在较高、高易发区的点密度相对较大，同时，结合ROC曲线结果分析，表明确定性系数模型更加适合于该区域的滑坡易发性定量评估。

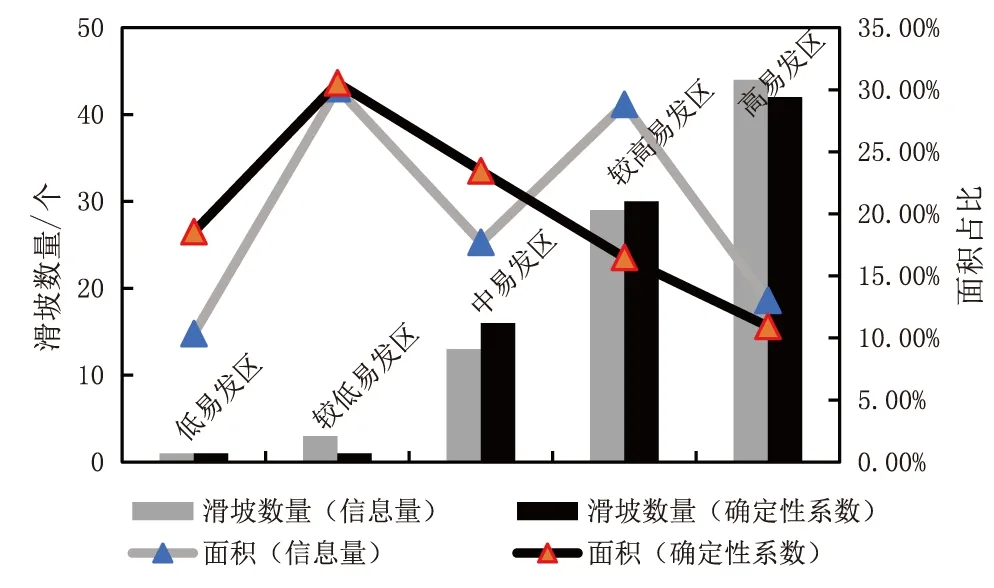
图5 不同模型易发性评价结果统计

4 结 论

(1)以四川省雷波县为研究对象，选取了高程、坡度、坡向、归一化植被指数、距道路距离、距河流距离、距断层距离、地层岩性作为滑坡易发性评价因子，采用了信息量模型、确定性系数模型进行滑坡易发性评价，得出了雷波县滑坡易发性分区图。

(2)两种模型评价结果都显示高、较高易发区集中分布在距离道路、河流、断层较近和地层岩性脆弱的地区。信息量模型分区结果：低易发区10.34%、较低易发区30.2%、中易发区17.7%、较高易发区28.82%、高易发区13.03%；确定性系数模型分区结果：低易发区18.57%、较低易发区30.55%、中易发区23.46%、较高易发区16.49%、高易发区10.93%。滑坡点数量上，信息量模型与确定性系数模型分别有81%、80%的滑坡点位于较高和高易发区。滑坡易发性评价结果与野外灾害调查结果比较一致。

(3)通过分析ROC曲线结果信息量模型(AUC=0.829 9)、确定性系数模型(AUC=0.893 5)，后者ROC精度更高，表明确定性系数模型在该区域滑坡易发性评价中评价结果与预测能力较好，更加符合该区域实际滑坡的分布情况，适合于该区域的滑坡易发性评价。结果表明，由ROC曲线与确定性系数相结合的滑坡易发性评价方法，具有一定的准确性和可靠性，可以为滑坡灾害易发性评价提供依据。