基于二维卷积神经网络高层数据特征学习的过程故障检测

李 元, 杨东昇， 李大舟

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)

化工生产过程系统正快速向着大型化、复杂化发展，在带来经济效益的同时也使得设备故障和人员受伤的几率增大.与传统工业环境相比，这些系统发生故障，一方面带来经济方面的损失，另一方面还有可能引起爆炸、火灾、毒气泄漏等特大事故，从而给社会、人员和环境带巨大的伤害.所以，确保化工过程安全、可靠，故障检测的准确性具有十分重要的意义.故障检测的研究也成为大量海内外专家学习和研究的热点[1-4].

故障检测技术包含4大类：(1)基于专家系统的诊断方法;(2)基于多元统计分析的诊断方法;(3)基于机器学习的诊断方法;(4)基于深度学习的诊断方法.其中专家系统包括浅知识专家系统和深知识专家系统，具有知识获取方便、形式统一、维护简单等优点，但存在知识集不完善、过分依赖专家经验和推理速度相对较慢的缺点.常用的多元统计分析方法包括主元分析(principal component analysis,PCA)[5]、基于k近邻的方法(k-nearest neighbor,kNN)[6]、偏最小二乘法(partial least squares,PLS)[7]，以及独立主元分析(independent component analysis,ICA)[8]，具有方法简单、数学解释性强的优点，但是针对化工过程数据的多模态、非线性问题并不能妥善处理.机器学习包含了人工神经网络(artificial neural network,ANN)[9]、支持向量机(support vector machine,SVM)[10]、高斯混合模型(Gaussian mixture model,GMM)[11]等，具有特征学习能力强的优点，同时也存在着故障检测率低的不足.深度学习包含了深度信念网络(deep belief network,DBN)[12]、卷积神经网络(convolutional neural networks,CNN)[13]等，具有可通过捕捉输入样本的模式特征、通过网络连接的方式提取出最高层的特征、再将其分类的优点.

目前已有一些专家学者将深度学习中的卷积神经网络用于故障检测与诊断中，并且获得了一定的成果.李辉[14]等将二维卷积神经网络用于变压器的故障检测，提出一种将一维样本数据转为二进制二维数据的检测方法和流程，并且取得相对较好的成果.赵东明[15]等将一维卷积神经网络用于柴油发电机的健康评估，提出一种基于卷积神经网络的健康评估方法，并与常用的BP神经网络对比，在准确率和识别速度上都有了明显的提升.吴春志[16]等将卷积神经网络用于齿轮箱的故障诊断，利用一维卷积神经网络模型对齿轮箱故障进行检测，该模型对单一和复合故障检测准确率均高于传统检测方法.Wen[17]等提出一种基于卷积神经网络的智能故障检测方法，在凯斯西储大学电机轴承数据集上进行了实验，获得了预测精度高达99.51 %的成果.Zhang[18]等提出一种基于扩展深度信念网络，利用DBN子网络提取故障数据的时空特征，利用全局反向传播网络进行故障分类，并且获得平均故障检测率高达82.1 %的成果.尽管以上算法用于工业故障检测可以获得较好的成果，但是针对化工过程中的非线性、高噪声、非高斯分布问题，尚存在识别速度慢、识别准确率低、误报率高等问题[19].

针对以上提出的问题，本文以传统的田纳西-伊斯曼(TE)化工过程数据作为研究背景，应用二维卷积神经网络(2D-CNN)方法对TE过程构建故障分类模型，将此模型用于TE过程11个操纵变量的处理.使用卷积神经网络中的卷积层进行特征提取和池化层进行特征降维学习原样本数据中高层的抽象特征，再将抽象特征输入全连接神经网络分类器，训练该神经网络识别不同的故障.经过训练的模型用在TE化工过程数据中,获得了以下良好的优势：(1)因输入层样本由多个采样样本组成，可以快速采集样本并将该段时间内采集的样本批次处理，所以，能够应用于对实时性要求高的故障检测领域，实现快速诊断的效果；(2)对训练的样本组合式预处理，使得卷积神经网络模型训练的时间大幅减少，同时检测率和误报率也相应地提升和降低.

1 卷积神经网络基本原理

1.1 卷积层与池化层前向传播

卷积神经网络主要是通过卷积核对局部范围内的特征进行提取，卷积层中每个神经元连接数据窗的权重是固定的(参数共享)，每个神经元只关注一个特征.其中卷积核的滑动使得对全局的局部特征进行整合，以此来获取整个样本的信息.卷积核每滑动到一个位置，将对应位置的数据与卷积核对应位置的值相乘并求和，得到一个特征图矩阵的元素.一般，卷积层为

(1)

其中:l代表层数;K为卷积核;Mj代表输入层的感受野.每个输出特征图都有一个偏置b，卷积核的操作流程如图1所示.

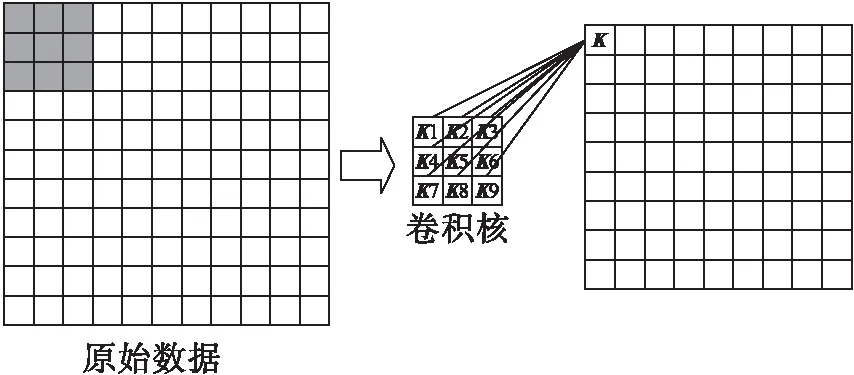
图1 卷积核操作示意图

卷积层对原数据进行多个卷积运算产生一组线性激活响应，而非线性激活层是对之前的结果进行了一个非线性的激活响应.卷积神经网络使用的激活函数一般为修正线性单元(rectified linear unit，RELU)，特点是收敛速度快，能够有效地防止梯度消失的问题.RELU函数的形式如图2所示，函数

f(x)=max(0,x) .

(2)

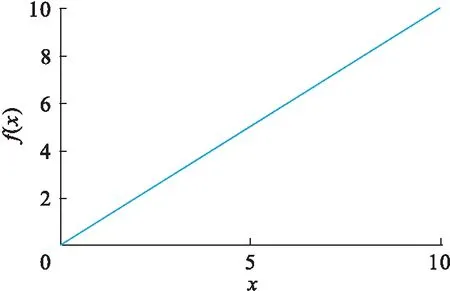
图2 RELU函数

经过RELU修正后的数据进入池化层,使用步长为n×n的最大池化(max-pooling)选出n×n范围内的最大特征值作为该池化的输出.池化层的主要作用就是减少特征图的尺寸，降低特征维数，同时一定程度上增加网络模型对特征缩放、扭曲的鲁棒性.池化操作的形式为

(3)

其中:MaxPolling(·)为池化函数；∂为权重系数.

1.2 全连接层的前向与反向传播

常用的全连接层神经网络大多为误差逆传播算法训练的多层前馈神经网络(back propagation，BP)，具有较强的非线性映射能力.常用的全连接层神经网络结构如图3所示.

图3 全连接层神经网络基本结构

其中全连接层输入参数为经过卷积神经网络中池化层降维处理并且拉伸为一维向量的样本数据.网络的输出参数y1,y2,…,ym为网络分类输出的概率值;d1,d2,…,dm为样本中原始数据的标签值，通过误差计算层计算出输出误差，再反向更新网络中隐含层与输出层的权重系数.

全连接层中隐藏层的激活为

(4)

经过不断重复上式的计算，最终求得网络的输出y1,y2,…,ym,利用网络期望输出和实际输出的差值，得出网络输出的误差.常用的误差函数为均方误差函数，公式为

(5)

其中:dk为理想输出；yk为实际输出；K表示输出神经元的个数.

全连接网络的迭代终止于Ek达到预设精度或大于设定的迭代次数，最后通过对误差函数与全连接神经网络中的权重关系，使用梯度下降法来获取最优权值为

(6)

(7)

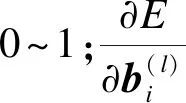
模型完成一整个反向传播更新权值参数后，将网络输出的结果经过sigmoid函数进行二分类.sigmoid函数多用于二分类问题中，它可以将整个实数区间映射到(0,1)区间内，sigmoid函数为

(8)

其中x为上一层神经元输出的结果.

1.3 卷积层的反向传播

在一个卷积层中，上一层的特征图被一个可学习的卷积核进行卷积运算，然后通过激活函数，就得到了输出特征图，这个输出特征图可能是包含了多个输入特征图的卷积输出，对于卷积层的每一种输出的特征图xj有[20-25]

(9)

因其第l+1层为池化层，同样也相当于是做卷积操作.为了求取单个样本的误差代价函数对参数的偏导，定义节点灵敏度δ为误差对输出的变化率[25-26]，即

(10)

式中若采样的因子是n，只需要简单地将每个像素水平和垂直向上拷贝n次，就可以恢复原来大小.

因为连接的权值是共享的，因此给定一个权值，需要对所有与该权值有联系的连接对该点求梯度，然后对这些梯度进行求和，使用(u,v)代表灵敏度矩阵中的元素位置，求得误差函数对偏置b的偏导与误差函数对卷积核K的偏导为

(11)

(12)

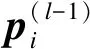
2 基于卷积神经网络学习模型的故障检测

卷积神经网络(convolutional neural network,CNN)是一种常见的深度学习网络框架，通常是含有卷积层、池化层、全连接层的神经网络，能够对高维数据特征进行提取和分类，进而实现数据本质特征的发掘.此前该方法广泛应用于图像识别、图像检测、语音识别等领域，并取得了很好的效果.

2.1 基于卷积神经网络高层数据特征的故障检测步骤

给定原始数据X.

(2) 通过专家经验对原始数据进行标签的标注处理；

(3) 提取训练和测试数据中的标签样本；

(4) 将不含标签的样本经卷积层操作产生一个特征映射来表明某些特征在输入样本中出现的位置；

(5) 将步骤(3)中输出的特征映射矩阵经过池化层的降维处理，输出一组低维度的特征矩阵；

(6) 再对步骤(4)输出的数据经过一组卷积层和池化层的特征提取、降维操作，接着将重构的特征压缩为一维数据，将其做为全连接层神经网络的输入，并通过全连接神经网络输出预测结果，最后将预测结果与标签对比得出误差，并通过反向传播算法更新全连接神经网络和卷积层的权重和偏置；

(7) 使用含标签的测试样本对模型进行评估，若训练误差与测试误差均符合设定的要求则保存模型，否则，继续执行(4)、(5)、(6)步骤，直到满足要求.

其流程如图4所示.

图4 卷积神经网络故障检测流程图

2.2 卷积神经网络模型的基本结构

卷积神经网络模型如图5所示.根据输入样本的大小为11×11的二维数据，考虑其卷积核大小、卷积核移动步数(步长)、卷积核个数、卷积层数与其结果准确率的关系，网络参数如下：

第一层为卷积层，使用16个4×4大小的卷积核，横向纵向步长均设置为1时，可得到特征为8×8的特征图，再经过2×2最大池化，横向纵向步长设置为1后，输出的为16个4×4的特征图.

第二层卷积层使用了16个1×1大小的卷积核，横纵向步长设置为1，得到16个4×4的特征图，再经由2×2最大池化，横纵向步长设置为1后，输出的为16个2×2的特征图.

在进入全连接层之前，将16个2×2的数据展开为一维向量，目的是将高维数据降到低维，为全连接层提供特征数据.

最后使用sigmoid函数对神经网络的输入进行分类.

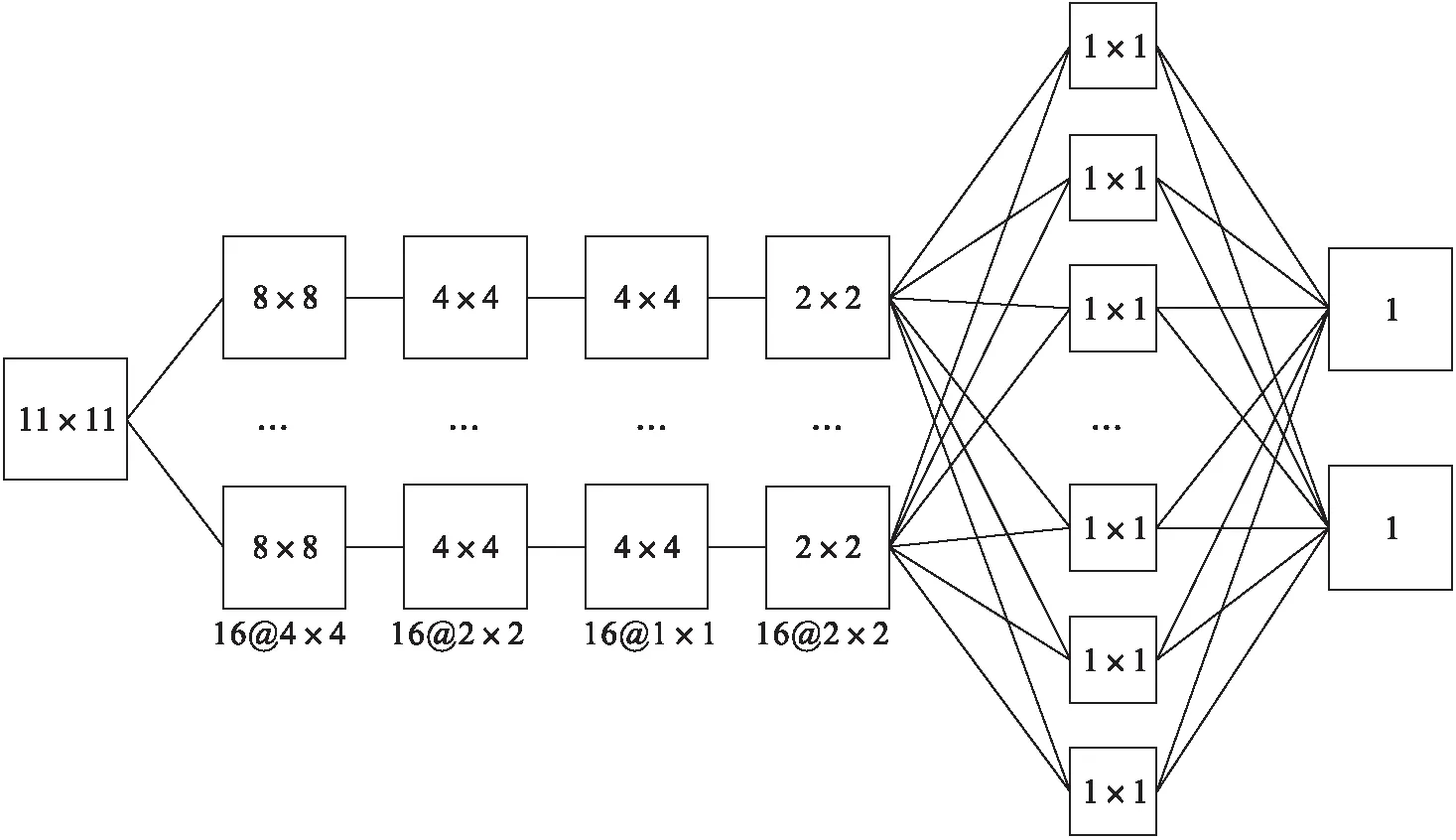
图5 卷积神经网络基本结构

3 TE生产过程的仿真研究

3.1 数据采集

数据来自田纳西-伊斯曼化学公司某实际化工生产过程提出的一个仿真系统.该流程作为通用测试平台得到了广泛的应用.TE工艺有12个操纵变量和41个被测变量，分别位于混合器、反应器、冷凝器、分离器、压缩机、汽提器等6个主要操作单元中.对TE过程的模拟包括1种正常状态和21种故障状态，分别发生在测试数据集的第161个样本点.

TE过程数据由训练集和测试集构成.训练集又分为正常状态训练集和故障状态训练集.其中正常状态训练集由500个样本点、52个变量组成，构成500×52维度的正常样本；故障状态训练集由各种类型故障的500个样本点、52个变量组成，构成共计21组500×52维度的故障样本，每组样本对应其中一种故障.测试集分为21组包含故障状态的测试样本，其中每种故障仅存在于一组测试样本中.样本由960个样本点、52个变量组成，其中测试集前160个样本点均为正常状态，故障在第161个样本点时刻引入，960个样本点时刻截至，构成960×52包含正常和故障的样本集.本文只使用了TE过程中最主要的11个操纵变量，这些变量与生产过程的状态密切相关.

本文中训练模型使用的数据同样也由训练集和测试集构成.训练集由495×11的正常状态样本与495×11的故障状态样本组成，构成21组，每组仅包含一种故障的训练样本，样本均从TE过程数据的训练集中不放回地随机抽取，再对训练样本中的正常和故障样本标注标签后构成一个维度为990×12的带标签训练集.测试集由550×11的正常状态样本与550×11的故障状态样本组成，其中正常状态样本由21组故障测试集的前160个正常样本组成3360×11的正常样本，再随机不放回挑去550个样本点做为测试集中的正常状态样本；故障状态样本由故障测试集中第161个样本到960个样本中随机不放回抽取的550个样本所组成；最后对正常状态样本和故障状态样本标注标签后构成一个维度为1100×12的带标签测试集.

3.2 仿真实验结果

利用已经搭建好的分类模型对TE过程进行故障评估，再与BP神经网络的分类准确率、误报率进行对比.为了保证模型对比的一致，其中BP神经网络的激活函数、隐藏层数、神经节点数与二维卷积神经网络参数一致.因二维卷积神经网络的输入为二维数据，所以在同一训练集和测试集情况下，二维卷积神经网络的训练和测试样本数分别为90个和100个，而BP神经网络是对单样本进行处理的，所以测试和训练样本个数各为990个和1100个.

使用TensorFlow架构来实现化工过程故障检测模型，因此，可以使用TensorFlow自带的神经网络工具箱函数来搭建该模型.为获得更好的效果，现对2D-CNN神经网络参数进行优化，表1所示为2D-CNN准确率与学习率和附加动量之间的关系.由表1可知：当学习率为0.01、附加动量为0.9时，模型的准确率高达100 %，且训练误差最低.由图6可以看出：相校于BP神经网络，2D-CNN具有较小的训练误差.

表1 2D-CNN准确率与学习率及附加动量的变化关系

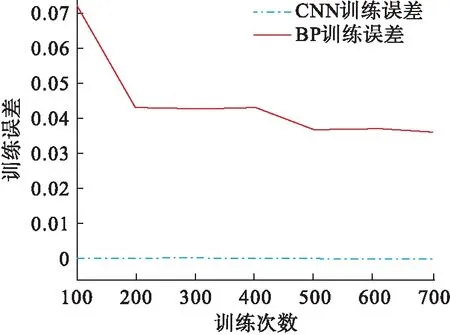
图6 两种算法的训练误差与迭代次数之间的关系

选取TE过程的故障1、5、8、11、13、14、17来验证算法的有效性.实验结果如表2所示.

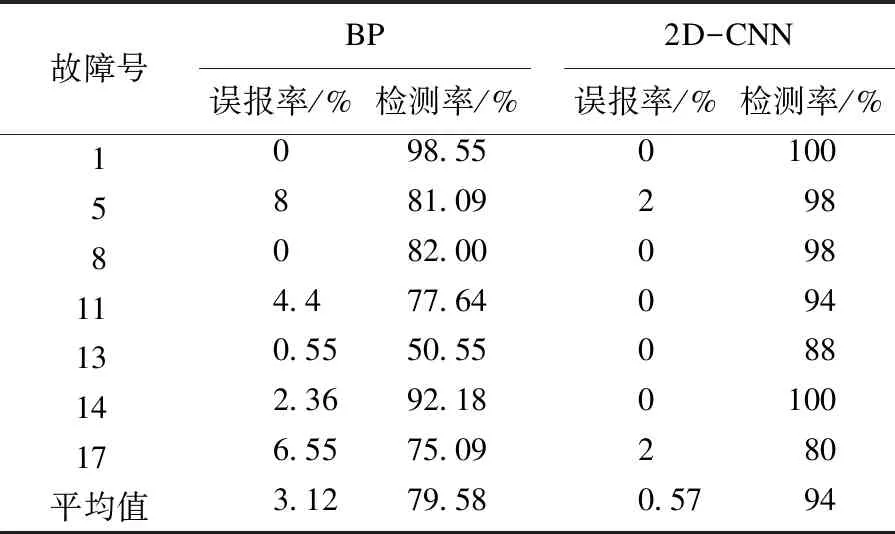
表2 两种算法的误报率和检测率

对于同样的训练数据，BP神经网络和2D-CNN的误报率和检测率如表2所示.BP神经网络采用传统神经网络的预处理模式，通过对样本的不断迭代学习，输出分类结果.BP神经网络对TE过程的7种故障都能较为准确地识别出，而且其误报率相对较低，但是TE过程为化工连续过程，BP神经网络只考虑单个样本中变量之间的关系，而没有考虑到前一时刻和现在时刻数据之间的特征关系.对比2D-CNN，经过多个样本之间的特征学习，提取出化工过程连续样本之间的高层关系，使得检测率有了明显增加，特别针对故障11和故障13，2D-CNN的分类准确率分别增加了16.36 %和37.45 %，误报率降低了4.4 %和0.55 %.对于故障5、8、14、17，2D-CNN的检测率都明显优于BP神经网络，且能够保证误报率相对较低.对于故障1，因其故障尺度较大，BP神经网络和2D-CNN均能较好地分类识别.

选取卷积神经网络检测率较高的3种故障(故障5,11,14)进行结果分析，图7给出了这3种故障的分类结果图.神经网络分类结果输出的为概率结果，设定类别概率值大于0.5就分为对应类别，其中正常样本标签为1，故障样本标签为2.

对于所选的3个故障，在检测出故障后，此后的故障都能被良好地识别出来，达到了较高的检测率.针对故障5和11，由图b和d可知：BP神经网络的故障分类从第557个样本开始才正确检测出来，而后的过程中仍有大量故障没有检测出来，而错误的将其分为正常类.由图a和c可知：2D-CNN的故障分类从故障一开始的第一时刻就已经正确识别出来，此后的所有故障都被正确地检测出来，仅故障11的故障样本有两处分类错误.而针对故障14，由图e和f可知：BP神经网络在故障发生后第555个样本才开始检测出故障，且正常样本中存在大量误报样本，故障样本中也同时存在分类错误的样本；而2D-CNN在故障发生的第一时刻就检测出来，同时正常样本中和故障样本中均无错误分类的样本存在.

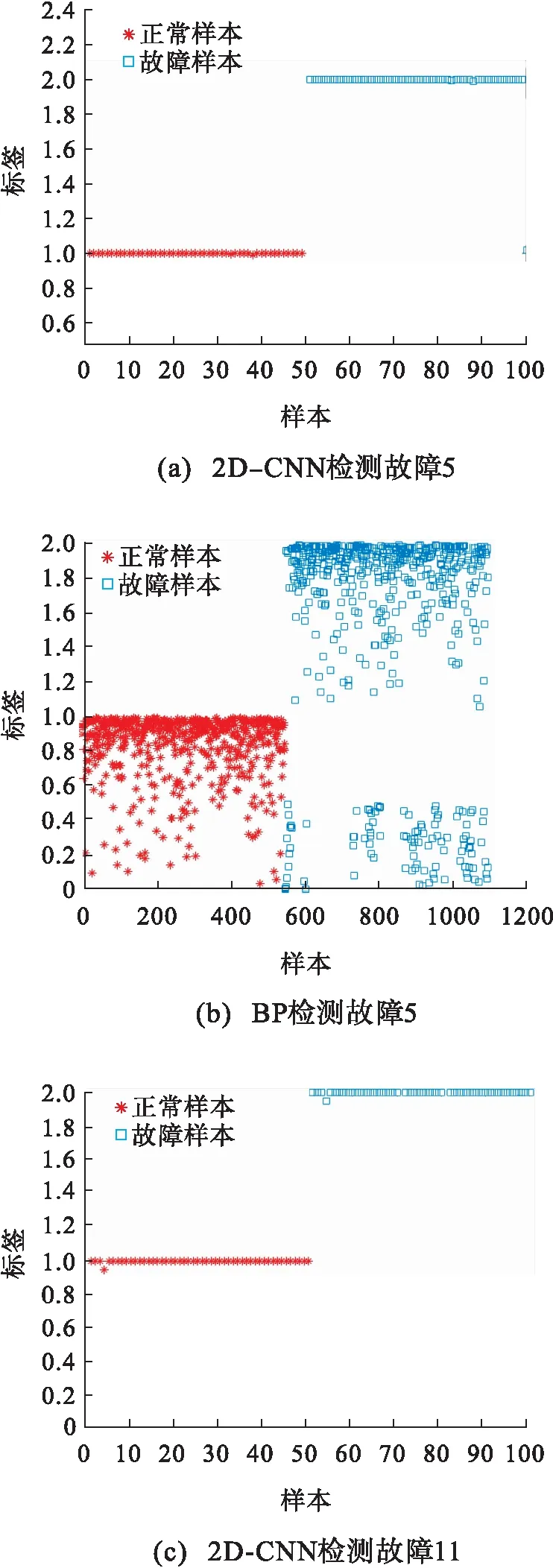
图7 2D-CNN与BP神经网络的分类分析结果

4 结 论

提出使用二维卷积神经网络(2D-CNN)找到TE化工过程数据故障各自对应的高层特征，通过卷积、池化、反向传播等操作实现数据的特征学习、特征重构，并且使用不同的神经网络方法进行对比，得到以下结论：卷积层的输入需要大量样本，使用卷积神经网络能够实现实时的样本采样和检测，使得该神经网络模型可以很好地使用在实时的故障检测系统中；卷积核在样本数据中的滑动能够很好地寻找到不同时刻样本与样本之间、变量与变量之间的潜在特征关系，得到最能反映原始数据中特征的隐藏变量.TE应用结果表明，二维卷积神经网络相较于BP神经网络，其检测率得到提高，同时误报率相对较低，很好地验证了该算法的有效性.