刚性变弯度机翼设计及低速风洞试验研究

冒 森， 杨 超， 谢长川， 孟 杨

(1.成都飞机工业(集团)有限责任公司技术中心，成都 510100;2.北京航空航天大学 航空科学与工程学院，北京 100191)

从莱特兄弟1903年第一架飞机的试飞成功开始，优化飞机的气动性能，实现更为高效、机动及安全的飞行一直是飞机研制的重点。未来飞行器朝飞行任务多样化、飞行条件多变以及实时调节飞机的飞行性能等方向发展，传统机翼已无法始终保持飞行过程中所需的最佳气动外形。变弯度机翼无论从基础的空气动力学方面还是工程实用角度都具有极大潜力[1-2]，采用变弯度机翼自适应技术的飞行器能依据飞行环境和任务的变化实时调整机翼弯度来提高飞行效率，增强机动性，以适应复杂多变的任务环境，被认为是未来实现航空技术新突破的主要研究方向之一。

从以往的研究可以看出，变弯度机翼的研究方法主要有仿真计算和试验研究两方面。仿真计算具有成本低、速度快、精度高等优点，在初始设计阶段和后期结构优化方面发挥了重要作用。Fujiwara等[3]以可变后缘的远程宽体跨音速客机为研究对象，采用CFD/CSD流固耦合计算并优化了机翼后缘气动外形和翼盒结构，使得巡航状态下全机减少了4.7%的燃油消耗。聂雪媛等[4]通过相似的方法研究柔性飞行器大变形时的静气动弹性问题。李哲等[5]利用几何拓扑的方法对柔性变弯度机翼结构进行优化设计。Mao等[6]基于几何精确涡格法对采用压电片驱动的变后缘二维翼段进行分析，很好地描述了压电变弯度机翼的气动非线性特性。倪迎鸽等[7]则是通过有理函数拟合非定常气动力研究了具有铰链间隙的折叠变形机翼的非线性气动弹性时域响应。但变弯度机翼结构普遍难以建立精确的数学模型，并且变弯度机翼实际变形能力有限，这导致仿真计算结果和实际结果差距比较大。因此，仿真计算不能作为判断变弯度机翼设计的唯一标准，需要和试验分析相结合。

试验研究作为变形机翼主要的研究手段一直也是变弯度机翼的研究热点。试验主要有地面试验，风洞试验和飞行试验三种。地面试验主要目的是验证机翼的变弯度功能。Campanile等[8]基于柔顺机构提出了带肋变形结构，用碳纤维和金属铰链制造带肋结构，并在试验中验证了变形能力。Icardi等[9]设计并制作了形状机翼合金(SMA)驱动的柔性蒙皮变体机翼模型，机翼结构由夹心盒段、柔性蒙皮和柔性翼肋组成，能够实现机翼整体弯曲和局部表面变形。王晓宏[10]设计了一种利用形状记忆合金驱动的可连续变弯度机翼机构，将SMA丝布置于波纹状主动变形结构的谷底位置，通过形状记忆合金变形驱动整个结构变形。这些地面试验直观地反映所设计机翼的变形能力，但是没有引入气动载荷，其真实变形能力需要后续的风洞试验进一步验证。飞行试验是验证设计可行性的直接方案。NASA将可连续变弯度机翼机构与机翼固定盒段连接成为一个整体，机翼表面覆盖可变形蒙皮，将其运用到F-111飞机上，并进行了多次飞行验证试验，均取得了圆满成功[11-12]。Probst等[13]采用MFC(Macro Fiber Composite)作为驱动器，在空中对展长为0.5 m的无人机进行弯曲控制。飞行试验是变弯度机翼进行实际运用的最终手段，但是由于重复性差、准备周期长，并不适合于初步设计阶段。风洞试验可以准确测量包括气动特性和驱动功率，实际变形位移等变弯度机翼关注的物理量，具有重复性好、测控精度高等优点，在试验研究中承担承前启后的作用，因此绝大多数变弯度机翼的实验研究都集中在这一阶段。Woods等[14-15]提出了一种鱼骨主动变弯度机翼结构。风洞性能测试表明，这种结构能够提供很大的向上向下偏转变形的能力，并且对驱动能力要求较低。2015年，欧盟FP7项目开展了基于柔性结构技术的机翼翼尖变形装置的风洞验证[16]。Jenett等[17]公布一款模块机翼，该机翼可实现翼展方向的连续扭转变形。采用柔性臂实现翼尖扭转驱动，并在风洞试验中证明其相对传统机翼具有更加优越的滚转效率。刘逸峰等[18]设计了一种基于SMA驱动器厚度可变的机翼结构，并进行了地面加载和风洞试验，验证了设计方案的可行性。可以看出在研究初期，风洞试验可以快速准确的提供一些初始数据，为变弯度机翼初步设计提供重要的参考。另一方面，不同形式的变弯度机翼在风洞试验需求上并没有显著区别，因此开发可靠准确的变弯度机翼风洞试验平台，也是研究变弯度机翼的重要研究方向。

对于变弯度机翼的设计方案，国内外都开展了广泛而深入的研究。从现有的研究成果来看，变弯度机翼设计可以大致分为基于传统材料的机翼设计和基于新一代智能材料的机翼设计两大类。现阶段在全尺寸飞机上得到飞行验证的只有美国 FlexSys Inc.的无缝后缘变形方案[19-20]和欧盟Saristu的自适应变形后缘方案[21-23]两种，而这两种方案都是基于传统材料和常规驱动的变弯度机翼设计。侧面反映出当前阶段智能变形机翼从技术成熟度和结构可靠性角度还是有所欠缺的。因此，本文设计了一种基于传统材料的刚性分段后缘变弯度机翼结构(简称刚性变弯度机翼)，以此作为风洞试验的研究平台。该机翼结构共分为四个翼盒，各个翼盒之间通过转轴进行前后连接，并通过与转轴相连的舵机实现机翼结构弯度的变化。

本文分为三部分。第1章介绍刚性变弯度机翼的详细设计，通过气动力计算软件XFOIL对变弯度机翼的不同构型进行数值仿真计算，研究其气动性能。第2章设计变弯度机翼风洞试验平台，搭建测试采集系统，对刚性变弯度机翼进行风洞试验。第3章分析并研究仿真结果和风洞测试结果的变化趋势和差别。最后总结并评估刚性变弯度机翼的实际变形能力和风洞测试平台的性能。

1 刚性变弯度机翼的设计与分析

1.1 结构设计

本文提出的刚性分段后缘变弯度机翼结构由四段刚性翼盒组成。区别于柔性变弯度机翼，本文提出的变弯度机翼变弯度功能不涉及材料变形，而是通过舵机驱动翼盒之间的转轴实现，结构如图1所示。主要设计包括以下部分：①变弯度机翼结构段，包括机翼前缘段、机翼中段、机翼中后段以及机翼后缘段；②转动机构，包括舵机、转轴、联轴器等；③角度测试机构，包括角度传感器、可拆卸支架和转动轮。各个机翼结构段均是由纵墙、翼肋、蒙板等组成的翼盒结构，主梁安置在机翼前缘结构段中。机翼结构段之间通过部分翼肋与转轴相连，通过舵机带动与结构段相连的转轴实现机翼弯度变化。角度传感器通过传动轮与舵机相连，根据传感器转动角度和传动比间接计算出舵机的转动角度。机翼参考翼型是NACA0015，考虑到舵机的尺寸和安装形式，以及后续改进方案的需求，将从前缘到后缘4段翼盒占总弦长的比例设置为40%，17.5%，17.5%，25%。

(a)

(c)

1-机翼前缘结构段;2-机翼中部结构段;3-机翼中后部结构段;4-机翼后缘结构段;5-纵墙;6-翼肋;7-蒙板;8-转轴;9-舵机;10-角度传感器;11-可拆卸支架;12-传动轮;13-普通翼肋;14-加强翼肋;15-舵机翼肋;16-蒙皮。

图1 刚性分段后缘变弯度结构设计图与实物图

Fig.1 Structural design drawing and physical drawing of the rigid variable camber wing

为了保证刚性变弯度机翼为没有缝隙的封闭机翼。刚性翼盒设计为通长结构，翼盒表面布置蒙板，只在两个翼盒连接处留有细长的缝隙。翼盒之间的柔性蒙皮选择有机硅精密薄膜，这种薄膜弹性模量比较小并且不容易断裂，经预拉伸后进行粘贴到翼盒连接缝隙上。

给定机翼期望弯度，控制装置输出相应的电信号给舵机在舵机的驱动下，转轴带动与之相连的加强翼肋转动，从而使得与之相连的机翼结构段实现转动功能。同时，舵机带动与之相连的角度传感器转动，角度传感器读取舵机的转动角度并将其转化为相应电信号传输到控制装置，从而构成一套完整的角度测试系统。

1.2 气动分析

为了确定本文提出的刚性变弯度机翼的设计方案，使用XFOIL气动软件进行了初步分析，并比较刚性变弯度机翼，标准NACA 0015翼型以及传统带后缘控制面机翼的气动性能。XFOIL代码是基于势流理论，加入黏性边界层求解器来预测表面摩擦阻力和流动分离，提供了比无黏性代码更完整的阻力预测，且可在一定范围内考虑气流分离特性。XFOIL已被证明在计算二维翼型时与高精度的CFD计算结果具有可信度[24]。它的计算成本低，易于集成到MATLAB软件中，因此为模型设计中的中等精度气动力分析提供了一个理想的解决方案。

XFOIL的输入是翼型坐标和外部气动条件。为了准确得到机翼主动变形后的翼型坐标，本文采用翼型参数化方法，将刚性变弯度机翼翼盒的相对转角作为参数，生成机翼变形后的翼型坐标。具体方法为：首先选取翼盒表面上相当数量的坐标点为控制点，根据相对转角对控制点进行坐标旋转变换，生成新的控制点。并在翼盒关节处对控制点进行三次样条插值处理，最后重新插值生成新的翼型坐标。另外选取M=0.2，Re=106的工况作为外部气动力条件。这是无人机典型工况点，马赫数足够低，可以避免显著的压缩性影响，雷诺数足够大，可以避免低雷诺数时阻力的高度非线性增长。

本文中将前缘翼盒、第二段、第三段及后缘翼盒之间的相对转角分别记为转角1、转角2、转角3。每个翼盒向下偏转4°作为刚性变弯度机翼的典型气动外形，按转角顺序记做变弯度构型4-4-4。为了进行有效的比较，取弦长相同，且传统带后缘舵面翼型的最大升力系数将和变弯度构型4-4-4相同作为基准状态。通过分析计算，选择初始翼型为NACA0015的传统舵面翼型为研究对象，舵面长度设定为25%弦长，舵面向下偏转14.5°，达到两种翼型具有相同的最大升力系数。分析时假设传统带后缘控制面翼型是一个没有缝隙的封闭舵面，图中及后文简记为传统舵面翼型；无控制面偏转的NACA0015翼型简记为初始翼型，各翼型如图2所示。

图2 三种翼型的翼剖面Fig.2 Wing profiles of the three airfoil

图3(a)显示后缘向下偏转后，传统舵面翼型和构型4-4-4升力系数显著大于初始翼型。刚性变弯度机翼迎角为11°时，升力系数达到最大1.44，之后发生失速，升力系数减少。传统舵面翼型拥有相同的最大升力系数，迎角为12°时到达最大点。图3(b)显示当迎角大于10°时，阻力系数显著增加。表明临近失速时，通过增加迎角已经不能提升翼型升力，反而会额外增加阻力。考虑到XFOIL无法在大迎角失速状态下得到准确的阻力系数，此时的数据仅做为趋势参考。

图4显示的是迎角与力矩系数的关系，负值代表是低头，正值代表抬头。迎角为0°时，初始翼型的力矩系数为0，而传统舵面翼型和变弯度构型4-4-4有很大低头力矩系数。迎角大于-3.5°时，随着迎角的增加，传统舵面翼型和构型4-4-4的低头力矩系数减少，并且传统舵面翼型低头力矩系数大于构型4-4-4的。当迎角小于-3.5°，传统舵面翼型的低头力矩系数要小于构型4-4-4的力矩系数。综合升力系数与力矩系数的结果可以看出，对实际飞机而言，在正常飞行时，在同一迎角下，相对传统舵面翼型，变弯度翼型能够提供更大的升力而产生更小的低头力矩，这是变弯度翼型在实际应用中的优势之一。

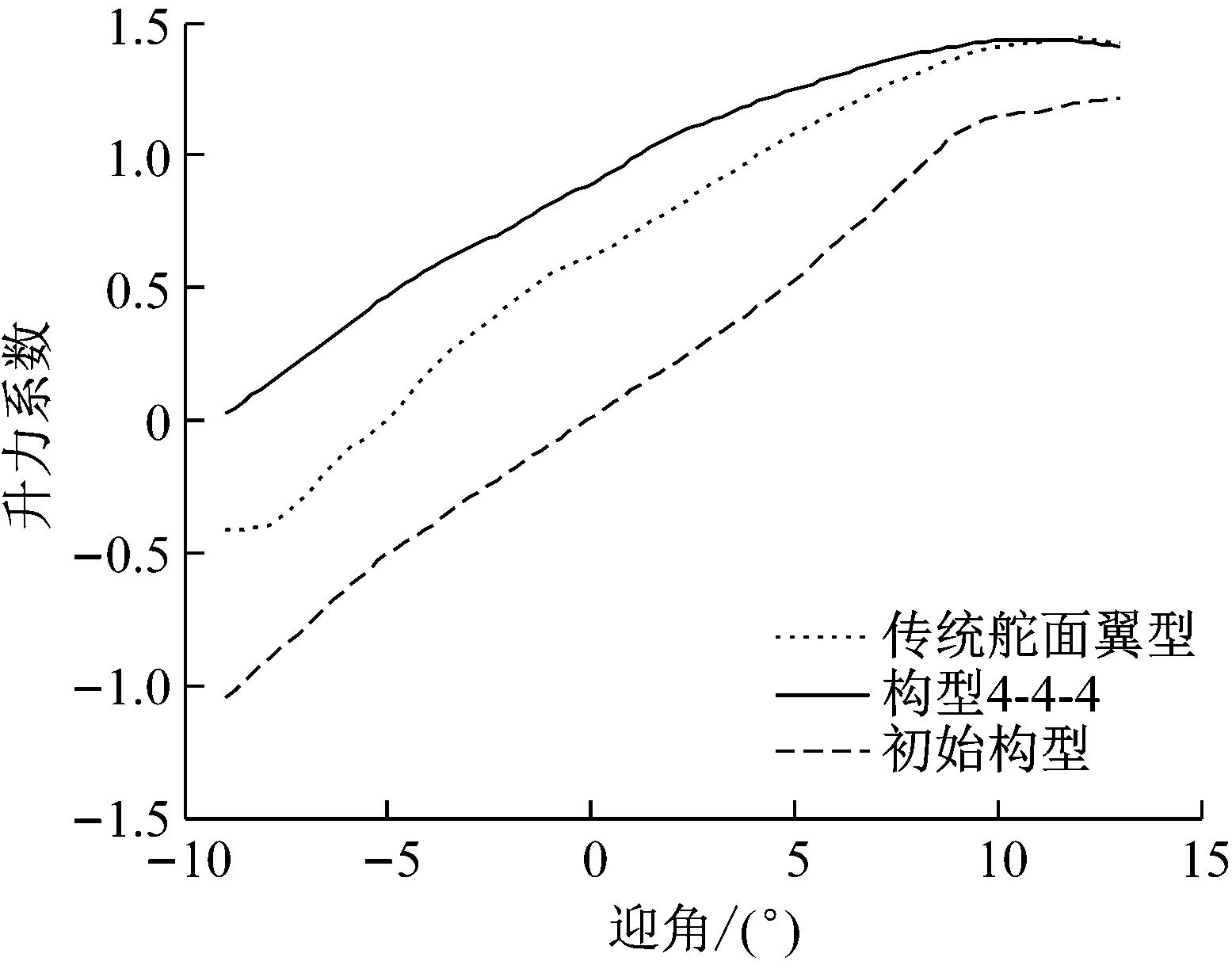
(a) 迎角与升力系数关系

(b) 迎角与阻力系数关系图3 二维翼型气动系数与迎角的关系Fig.3 Relationship of the 2D airfoils between aerodynamiccoefficient and angle of attack

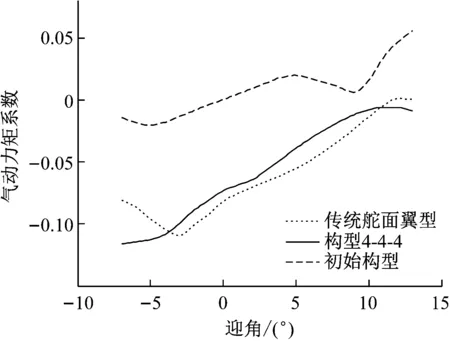
图4 二维翼型力矩系数与迎角的关系

图5为典型迎角下各翼型的压力系数(Cp)分布，横坐标为各翼型的弦线弧长。图5(a)显示传统舵面翼型和刚性变弯曲构型4-4-4的上下表面压力差均大于初始翼型，所以升力系数更高。构型4-4-4的Cp分布曲线整体上比较光滑，只在翼盒转角处有细微的突变。而传统舵面翼型在后缘部分则出现明显的气动压力上升，变化幅度剧烈。不光滑的Cp分布也是阻力增大的原因，变弯度机翼可以通过柔性蒙皮技术进一步提高压力分布的光滑度从而减少阻力，对比传统舵面翼型具有气动优势。图5(b)可以看出，迎角为-4°时传统舵面翼型的下表面压力系数对比迎角为-3.5°时显著减少，所以引起了气动力矩的突变。同等情况下，刚性变弯度机翼Cp分布整体变化不大，前缘升力减小。这与图4中气动力矩分布有一致性，因此变弯度构型4-4-4对比传统舵面翼型力矩曲线随迎角变化更平稳。

(a) 5°迎角，翼型压力系数分布

(b) -3.5°与-4°迎角，翼型压力系数分布图5 典型迎角下各翼型的压力系数分布

图6表示三种翼型的升力系数与阻力系数关系图6(a)为翼型极曲线，可以看出，当升力系数小于1.165时，变弯度构型4-4-4的阻力系数要明显小于传统舵面翼型，甚至小于初始翼型。当升力系数大于1.165时，传统舵面翼型和构型4-4-4有相当的阻力系数。此外，当升力系数大于1.165时，刚性变弯度机翼的阻力系数显著上升而此时升力系数增加缓慢，这对应了机翼大迎角时的状态。图6(b)显示了升阻比与升力系数的关系，该图进一步显示了用变弯度构型4-4-4相对于初始翼型和传统舵面翼型的优越性。构型4-4-4最大升阻比相对于初始机翼提高了34%，相对于传统舵面翼型提高了72%。当升力系数相同且都小于1.165时，构型4-4-4对比其他两种翼型都有较高的升阻比。这一点可以从图6(c)上得到验证，当迎角小于5°时，构型4-4-4的升阻比大于其他两种翼型，此时构型4-4-4的升力系数为1.165。值得注意的是，刚性变弯度翼型已显示出较好的气动性能，且此时未针对迎角状态优选配置各段偏角，而且对传统舵面翼型也未考虑缝隙的作用。

为进一步研究变弯度机翼的气动性能，选取变弯度构型4-4-4,3-3-2,4-0-2,1-0-3和0-0-2进行计算，得到升阻力与迎角的关系如图7所示，实线表示了几种构型升阻比外包络线。由图7可知，不同变弯度构型的最大升阻比对应的迎角不尽相同。翼型转角越大，最大升阻比对应的迎角越小。另外还注意到，变弯度构型越接近初始翼型，升阻比随迎角变化越平缓；变弯度翼型中弦线弯曲程度越大，升阻比随迎角变化越剧烈。图7中各构型的升阻比包络线证明，可以通过调整各段转角使得刚性变弯度机翼在较大的迎角范围内都能保持较高升阻比，这是传统机翼不能做到的，满足变弯度机翼始终保持最优气动外形的设计初衷。考虑到二维翼型和实际机翼的差别，刚性变弯度机翼的实际气动性能可能会低于计算预测值，但是三种构型的气动系数均通过统一分析工具得到，其相对关系具有明显的参考价值。

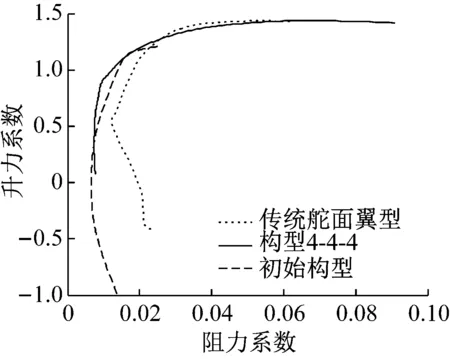
(a) 翼型极曲线

从上面的分析结果可以得到，本文设计的刚性变弯度机翼对比传统舵面翼型具有更好的气动性能，同等升力下，阻力更小，气动力矩随迎角变化更平稳，并且能在一个较大升阻比下扩展迎角范围。提供的翼型参数化方法可以正确反映翼型变化，结合XFOIL气动力计算软件，可以很好的分析不同翼型的气动力系数，计算耗费小，计算速度快，作为变弯度机翼初步阶段的气动分析工具是可行的。

图7 刚性变弯度机翼不同构型迎角与升阻比关系

2 风洞试验设计

针对本文研究需求设计了一种低成本的变弯度机翼风洞测试专用平台，可以便捷地改变机翼对来流地迎角，并对机翼在各种迎角来流下的升力、阻力、俯仰力矩进行测试，为变弯度机翼的气动力辨识，控制系统建模，主动气动弹性控制等研究提供初始数据。作为变弯度机翼研究的初始阶段，本文重点测试刚性变弯度机翼不同构型下的气动力，对比仿真计算结果，评估其在气动力作用下的真实变形能力。

2.1 试验模型描述

试验模型为矩形机翼，弦长360 mm，展长700 mm，如图8所示。翼盒结构为木质材料，总质量510 g。机翼主梁布置在弦长22.2%处，主梁为一通长的铝管，壁厚2 mm，外径20 mm，长度为800 mm。刚性变弯度机翼总共布置了三个舵机，两个舵机跟翼盒转轴同步直接驱动翼盒偏转，后缘翼盒舵机通过连杆结构驱动最后一段翼盒转动。翼盒中另外布置三个角度传感器，通过传动轮与转轴相连。所有舵机都选用Futaba BLS173SVI型航模舵机，其驱动力可以达到6.8 kg/cm，并且重量和体积都相对较小。柔性蒙皮材料为100 μm厚PDMS有机硅精密薄膜。

迎角调节盘可在±15°内较为精确调节机翼迎角，调节精度由转盘上的角度刻度盘确定，约为±0.1°。机翼轴套基座和迎角调节转盘用螺栓螺母连接，其套筒上有插销孔，用于固定刚性变弯度机翼的主轴，并防止其相对转动。

角铁、测力天平安装在风洞框架后，风洞试验前调节迎角时，首先固定住轴套与迎角调节转盘，随后按照对应的角度刻盘转动迎角调节转盘使测试翼段与来流达到一定迎角，再紧固相应连接，实现迎角调节转盘与测力天平一体固定。

图8 风洞试验支持系统Fig.8 Wind tunnel test support system

2.2 数据采集与试验监控系统

风洞试验相关设备主要包括稳压电源、低通滤波器、数据采集卡、工控机和监控机等，整个系统示意图见图9(a)，试验实物图见图9(b)。稳压电源的作用是给测力天平供电。低通滤波器的作用是将天平平台的采集信号中的高频噪声滤掉。数据采集卡以1 000 Hz的采样频率采集传感器感受到的模拟电压信号并将其转换成数字信号，再将数字信号输入到工控机，通过工控机计算产生控制指令传给可变弯度机翼上的舵机，控制可变弯度机翼的翼型弯度。监控机的作用是实时监控角度数据，保证试验模型的安全。最终，数据采集系统可以将数据采集卡得到的试验数据传递给上位机，通过Labview编写的图形界面直观地展示数据。

(a) 系统示意图

(b) 系统实物图图9 风洞试验数据采集与监控系统Fig.9 Acquisition and monitoring system of wind tunnel test

本次风洞试验主要通过六自由度测力天平监测模型根部测力数据，见图10，具体参数见表1，满足本文试验的测试需求。

图10 风洞试验天平Fig.10 Balance of the wind tunnel test

表1 测力天平参数Tab.1 Parameters of the force balance

在整个试验过程中，机翼的主轴与天平几何中心重合，机翼翼型弦线与天平X方向中线重合，保证天平获得的力的大小能代表机翼机体坐标系的受力。再由坐标系转化获得机翼的气动力特性，对于本次试验来说，具体转换关系如下

升力系数：

(1)

阻力系数：

(2)

力矩系数：

(3)

式中：Fx为天平X方向测力数据;Fy为天平Y方向测力数据;Mz为天平Z方向的力矩数据;l为主梁和气动中心的距离;α为机翼迎角;ρ为试验空气密度;v为试验段来流风速;S为机翼参考面积。

3 试验结果分析与讨论

开启风洞，风速设定为10 m/s，给舵机输入控制信号改变机翼的三个转角，通过监控器监控并记录翼盒实际转角，同时记录天平测力数据。迎角选取0°、2°、4°三个角度进行变化，转角选择为0°、2°、4°、6°四个角度进行变化。从迎角0°，构型0-0-0开始测量。首先固定迎角，然后按顺序分别变动4次转角3、转角2和转角1，每次测量仅独立变动一个角度，共需测量3×4×4×4=192个状态。运用式(1)～(3)，将天平测力数据换算为刚性变形机翼的气动力系数，记为测力试验值。通过迎角转盘和各翼盒相对实测角度，按1.2节分析方法计算得到对应构型的气动力系数，记为实测角度解算值。实测角度和指令角度按照试验顺序排列如图11所示。同时，按1.2节分析方法计算得到舵机输入角度对应构型的气动力系数，记为仿真计算值。

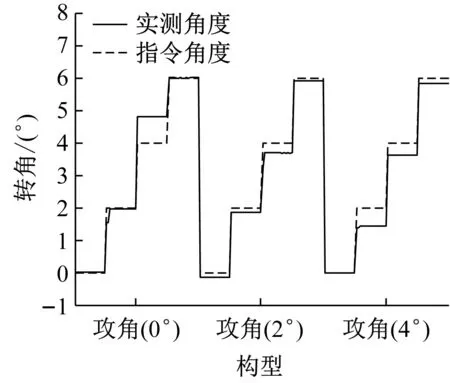
(a) 转角1

图11为转角实测角度和指令角度按照测试顺序排列。整体上实测角度和指令角度符合较好，平均相对误差为-4.32%，但是由于存在结构间隙和摩擦等不利因素影响，翼盒实际转角小于指令转角。又观察到机翼迎角越大，实测角度和指令角度差距越大，在转角1和转角3上体现得比较明显。这是由于迎角越大，机翼承受的气动力越大，航模舵机在大载荷下输出角度不稳定引起的。这是后续研究中需要改进的地方，这也说明了一个问题，开环形式的变弯度机翼很难保证精确的角度控制，即使是刚性变弯度机翼这种可靠性比较高的变弯度结构，需要通过有效的反馈控制才能到达预期的效果。

图12(a)为刚性变弯度机翼各构型在不同迎角下的升力系数，图12(b)为0°迎角下各构型升力系数，图12(c)为图12(b)黑色虚线框中放大图，显示的是转角1为2°时各构型升力系数。从图12(a)可以看出各构型的升力系数随着迎角增加而增大。三种结果随转角变化的趋势是一致的，实测角度解算值略小于仿真计算结果，平均相对误差为-5.81%，测力试验值则与仿真计算值吻合度略低，测力试验值和实测角度解算值的平均相对误差为-8.92%。实测角度解算值小于仿真计算结果是因为转角实测角度要小于指令角度。测力试验值总体偏低，其差异来源于两点，一方面XFOIL是基于面元法的气动力计算软件，二维翼型升力系数仿真计算结果会高于实际；另一方面由于三维效应的存在，二维翼型仿真结果也会比实际机翼模型的气动力系数高。

图12(b)分为四部分，每部分有16个变弯度机翼构型，表示不同转角1角度下的各构型升力系数。可以看出，变弯度机翼构型升力系数随着转角1角度增加而增大。图12(c)横坐标为具体构型。对比构型2-0-0,2-0-2,2-0-4,2-0-6的升力系数变化，可以得出保持转角1和转角2不变，增加转角3角度，变弯度构型升力系数增加。当构型2-0-6变动到2-2-0构型时，翼型的升力系数下降。这是由于变弯度机翼的转角3减少了6°，而转角2只增加了2°，转角3角度变化对升力下降的影响超过了转角2。这也是图12(c)中升力系数连线出现起伏的原因，类似的情况还出现在构型2-2-6到构型2-4-0等。此外，从构型2-0-0,2-2-0,2-4-0,2-6-0的升力系数变化，可以得出转角1和转角3不变，增加转角2的角度，构型升力系数也会增加。综上，对于本文中的变弯度机翼，增加转角角度，都会增加升力系数。原因是增加翼盒转角，相当于增加了局部迎角，使得翼型整体环量上升，从而引起升力增加。

(a)

为了研究各转角变化对变弯度机翼构型升力系数的具体影响，计算得到各转角平均单位角度升力系数增量与转角的关系，如图13所示。从图中看出，仿真计算结果和风洞试验值都表明三个转角的平均单位角度升力系数增量都随着转角的增加而减小。测力试验值的平均单位角度升力系数增量要小于实测角度解算值且小于仿真计算值，这和图12(a)中测力试验值升力系数要小于实测角度解算值和小于仿真计算值是一致的。相同转角下，转角1的单位角度升力系数增量大于转角2大于转角3。这是由于转角1转动，后续所有翼盒都保持相对转角整体在偏转，而转角3变化只相当于后缘翼盒发生偏转。不同转角变化对应不同的机翼面积偏转，所以变化转角1带来的机翼升力系数变化最大。因此对于刚性变弯度机翼，为了提高机翼升力增加转角1角度收益最好。

图14为刚性变弯度机翼各构型在不同迎角下的阻力系数。迎角和翼盒转角越大，阻力系数越大，这与升力系数的变化趋势一致。构型6-6-6是各迎角下的阻力系数最大的构型。各构型的阻力系数的实测角度解算值和仿真计算值的平均相对误差为-7.52%，测力试验值和实测角度解算值的平均相对误差为-13.22%，都要大于升力系数的误差。阻力系数的角度推算值与仿真计算值误差较大的主要原因是，XFOIL计算阻力系数时对刚性变弯度机翼构型转角误差更为敏感。考虑到机翼的三维效应，并且阻力系数测力试验值能正确反映转角变化对于机翼阻力的影响，其与仿真计算值误差是可以接受的。

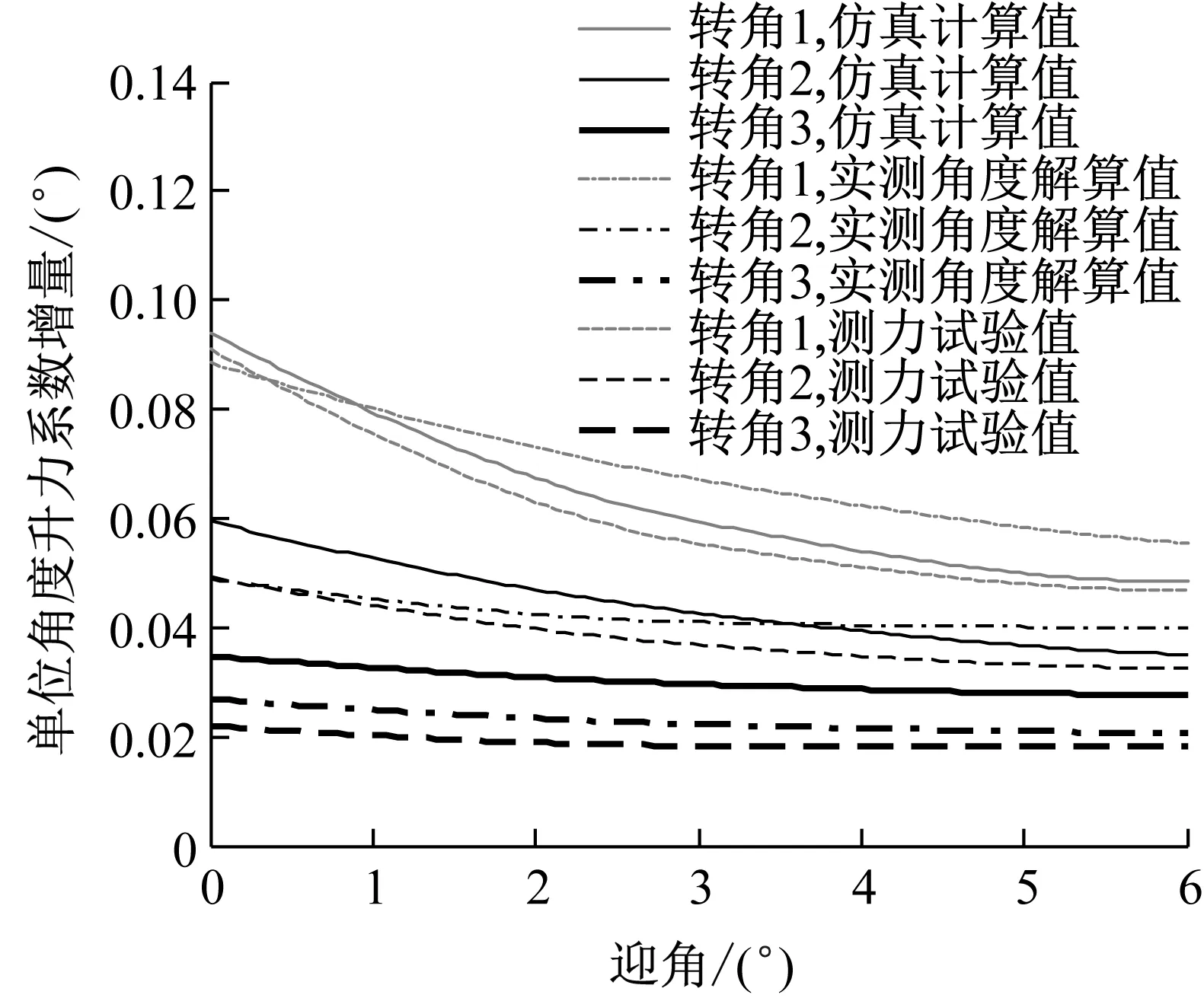
图13 平均单位角度升力系数增量与转角关系

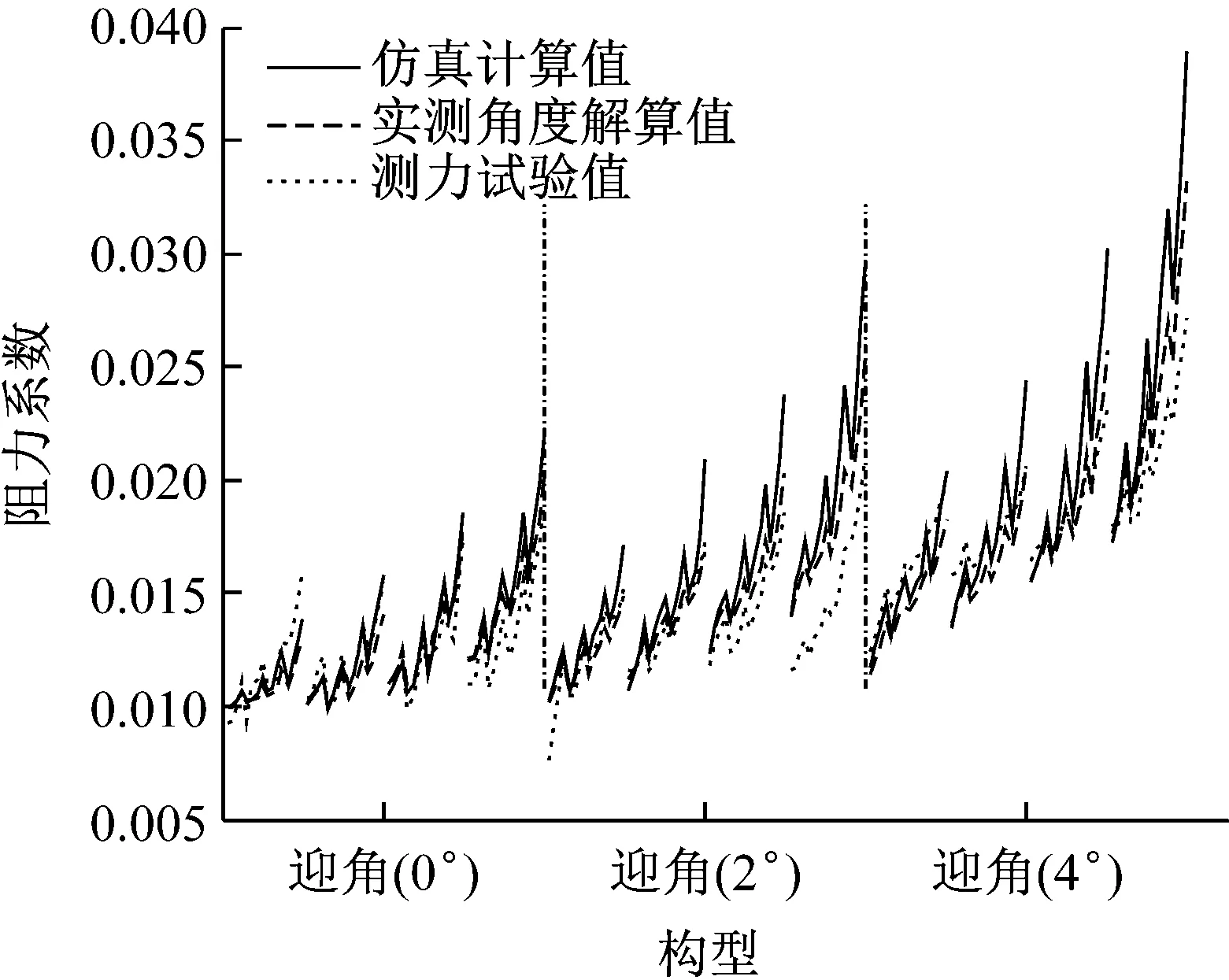
图14 刚性变弯度机翼各构型阻力系数

图15为各变形构型下力矩系数试验值和仿真计算值的比较。从中可以看出刚性变弯度机翼翼盒转角增加，产生低头力矩，随着迎角增加，低头力矩减少。最大的低头力矩系数是0°迎角下构型0-6-6产生的。变形机翼构型的力矩系数的实测角度解算值和仿真计算值的平均相对误差为7.28%，测力试验值和实测角度解算值的平均相对误差为6.77%，试验值跟仿真计算结果吻合得更好。计算得到各转角平均单位角度气动力矩系数增量与转角的关系，如图16所示。

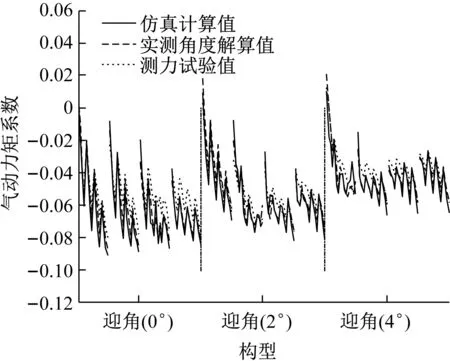
图15 刚性变弯度机翼各构型力矩系数Fig.15 Moment coefficients of the configurations of the rigidvariable camber wing

图16显示单位角度低头力矩系数增量随着转角的增加而减少。转角较小时，转角1提供的单位角度低头力矩系数增量最大，但是随着转角增加迅速减少。转角较大时，转角3的单位角度低头力矩系数增量最大，而且随角度变化不大。转角2单位角度低头力矩系数增量整体上小于转角3。这意味想要通过改变刚性变弯度机翼的气动力矩来调整飞机姿态，最好的办法是调整转角3的角度。

图17为不同迎角下刚性变弯度机翼各构型的升阻比。其中仿真计算值和实测角度推算值符合的很好，且都大于测力试验值。这主要是因为前两者是二维翼型的升阻比，忽略了机翼的三维效应，所以要大于测力试验值得到的升阻比。实测角度推算结果显示，0°迎角下4-4-2构型升阻比最大为102.4，2°迎角下2-2-4构型升阻比最大为85.32，4°迎角下构型1-2-0升阻比最大为77.55。随着迎角增加，变弯度机翼构型最大升阻比减少；迎角越大，最大升阻比对应的翼型转角越小。这和本文第二小节图7得到的结论是一致的。测力试验值表明，0°迎角下4-4-2构型升阻比最大为69.29，2°迎角下2-2-2构型升阻比最大为68.94，4°迎角下构型1-4-0升阻比最大为49.71。虽然测力试验值得到的不同迎角下最大升阻比构型与实测角度推算值有所不同，但是相关构型转角差别不大并且其变化趋势一致，进一步验证了本文提供的仿真计算方法的合理性。同时看到当构型转角等于6°时升阻比都比较小。因此刚性变弯度机翼要保持较高的升阻比，进行转角控制时尽量避免单一转角角度过大的情况，迎角增加时需要减少转角角度。

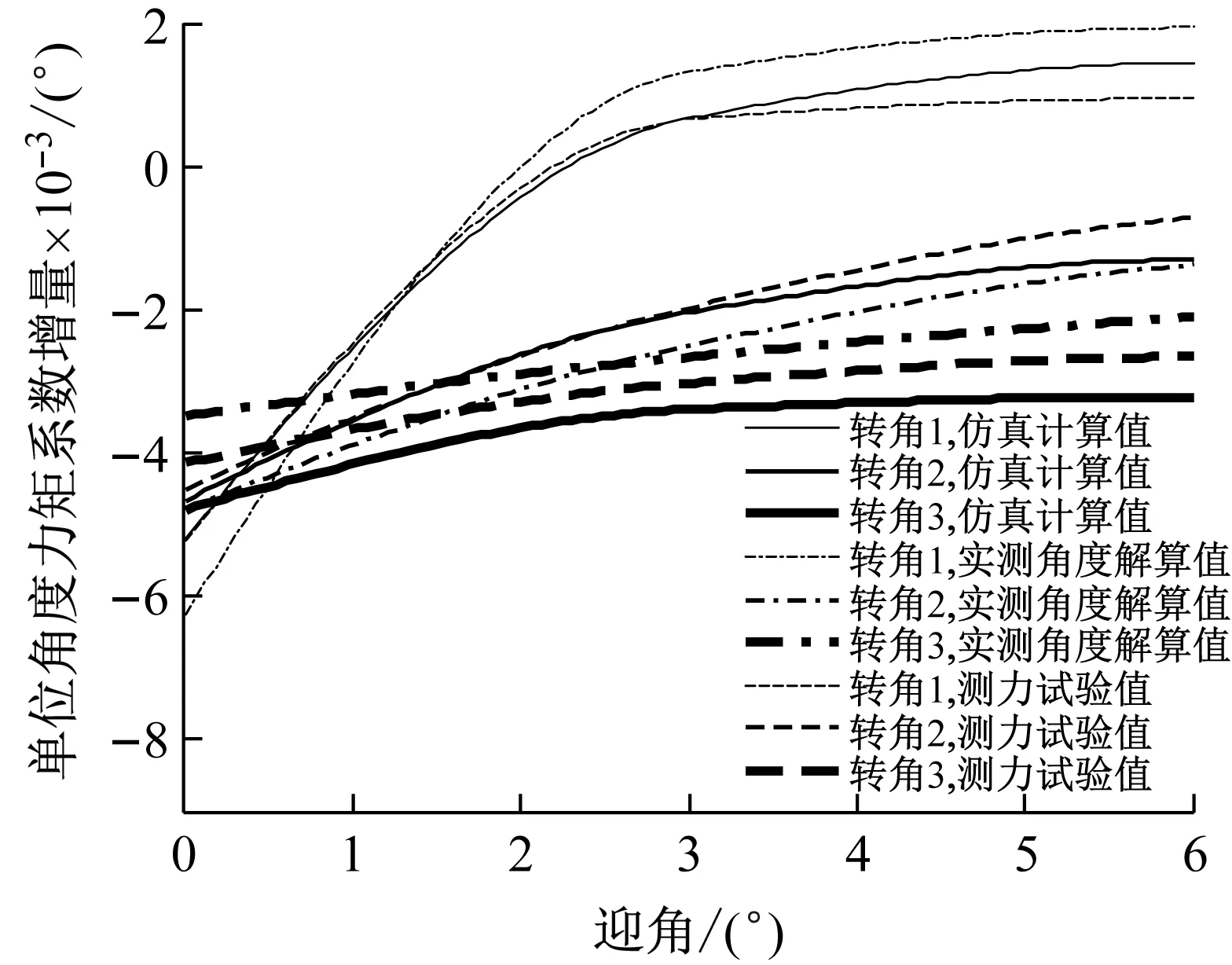
图16 平均单位角度力矩系数增量与转角关系Fig.16 Relationship between average increment of momentcoefficients per unit angle and rotation angle

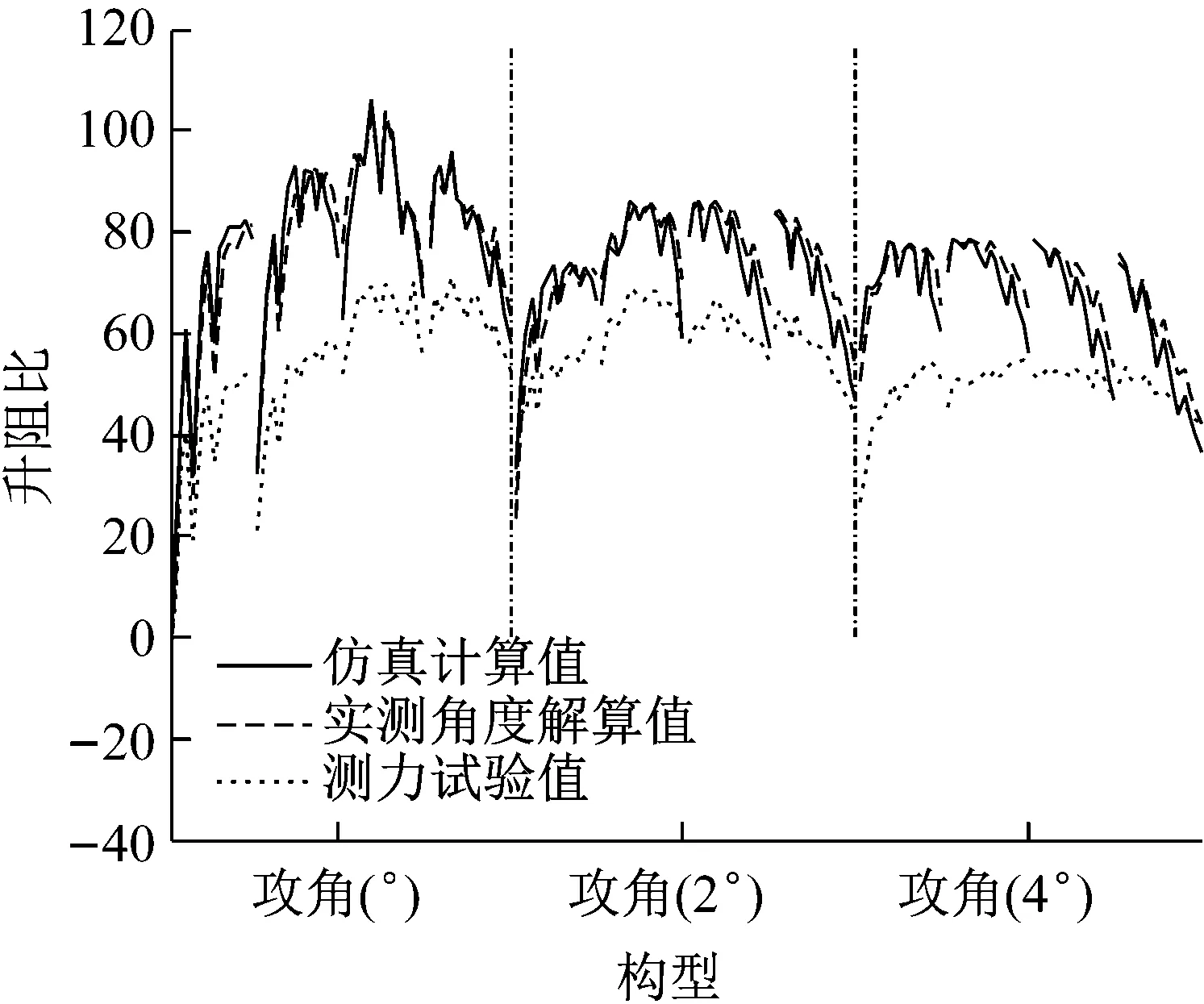
图17 刚性变弯度机翼各构型升阻比

结合上述分析，我们可以得到：① 本文设计的变形机翼风洞试验平台满足刚性后缘分段变弯度机翼气动性能测试要求。对于升力系数，实测角度解算值和仿真计算值气动系数的误差为-5.81%，测力试验值和实测角度解算值误差为-8.92%；对于阻力系数，实测角度解算值和仿真计算值的平均相对误差为-7.52%，测力试验值和实测角度解算值的平均相对误差为-13.22%；对于力矩系数，实测角度解算值和仿真计算值的平均相对误差为7.28%，测力试验值和实测角度解算值的平均相对误差为6.77%。总体来说，气动力系数的测力试验值的结果与仿真计算结果符合较好，能正确反映刚性变弯度机翼的转角变化对气动力的影响以及不同迎角下升阻比最大的变弯度机翼构型。② 对于本文提供的刚性变弯度机翼，翼盒实际转角和指令转角平均相对误差在5%以内，保证了结构变形功能。对于其飞行控制而言，增加转角1能显著提高升力，增加转角3则能显著提高低头力矩，避免单一转角过大并且在迎角增加的情况下减少转角可以保持高升阻比。

4 结 论

本文以一种刚性变弯度机翼为研究对象，将刚性变弯度机翼参数化后，结合XFOIL气动力计算软件，对变弯度机翼的不同构型进行数值仿真计算。在此基础上，设计变弯度机翼风洞试验平台，搭建测试采集系统，对刚性变弯度机翼进行低速风洞试验研究。分析仿真计算结果和风洞试验结果后，得出结论：

(1) 本文提出的刚性变弯度机翼作为变弯度机翼的一种设计方案，结构简单可靠，变形效果显著。仿真计算和风洞试验表明均表明其在增升减阻，保证高升阻比和提供机翼配平力矩的优势明显，并提出了对应的控制策略。但是实际控制中存在转角变形不到位的情况，需要对其进行角度反馈控制。

(2) 本文设计的刚性变弯度机翼风洞试验系统可以正确测量和记录不同迎角和构型下刚性变弯度机翼的气动力。通过本次多工况的风洞试验，其结构可靠性和易操作性都得到了验证，为仿真计算提供了数据支撑。作为变弯度机翼风洞试验平台可以在此基础上进一步开展变形机翼的动力学试验。

(3) 将刚性变弯度机翼参数化后，结合XFOIL气动力计算软件，可以快速的计算不同刚性变弯度机翼构型的气动系数。其作为刚性变弯度机翼的气动分析工具是高效可行的，能正确反映转角变化对刚性变弯度机翼气动力的影响，准确性得到了风洞数据验证。在后续研究中可以作为分析工具开展刚性变弯度机翼的气动外形优化工作。