集装箱坠落载荷作用下甲板板架结构响应理论预报方法研究
郭德松, 纵 帅, 王秀飞, 费宝祥, 王加夏, 刘 昆
(1.江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003;2.驻秦皇岛地区军事代表室,河北 秦皇岛 066000)
在经济贸易的带动下,港口业务日益繁忙,集装箱吞吐量不断增加。与此同时,港口码头发生集装箱坠落事故有增无减。由于在起吊作业过程中诸多环境因素以及人员操控的不可控性,钻杆、立/套管、集装箱、发动机等不慎坠落事件时有发生,往往会导致甲板等船体结构破损,危害舱室安全[1-2]。据英国石油部门在1980—1986年间所做意外事故统计,平均每年每台吊机作业超过4 500次,物体在每次起吊过程中的坠落概率约为2.2×10-5[3],足以引起设计者的关注。
在各类坠物中集装箱最为常见,其质量大、吊装高度高,一旦发生坠落事故,巨大的撞击动能会导致船体结构产生严重的损伤变形,威胁船体结构安全性[4]。针对于此,国内外学者已开展了一些研究工作。船舶碰撞场景中,结构损伤与箱型坠物相似,基于此,在一些船体结构碰撞研究中,Zhu等[5-7]研究了船舶及海洋板结构受重复撞击荷载时的损伤机理,建立了结构损伤的简化预报公式。刘昆等[8]对强桁材结构进行了试验仿真研究,为解析方法中变形模式的确定提供依据。Wang等[9-11]对舷侧外板的变形进行了研究,提出了多种结构损伤解析预报公式。上述研究可为箱型坠物解析方法提供参考。坠物损伤方面,郝瀛[12]研究了箱型坠物作用下甲板结构破损的临界变形能,确定了临界变形能的加权系数,进而得到板架整体的临界变形能,可为实际工程设计提供参考。刘伟等[13-16]对受坠落物体撞击作用后的海洋平台以及海底隧道结构动态响应过程进行了数值仿真,得到了结构的碰撞力、损伤变形及能量转换的一般性规律。目前针对船体坠物损伤的研究中多采用数值仿真方法且计算场景比较理想,然而实际事故中坠物形状、坠落状态和撞击位置均具有不确定性,且基于理论的简化预报方法可以更为便捷快速的得到结构损伤响应以指导设计及事故救援。应用简化解析法对重物跌落问题进行求解时,最重要的是得到结构损伤变形的主要特征并建立合理有效的数学模型。对于数学模型的建立可以是基于试验结果的观察,也可以是基于对仿真结果的分析[17-18]。因此,本文以船体板架结构为研究对象,考虑集装箱不同坠落撞击状态,基于塑性力学理论建立板架结构响应理论预报方法,分析集装箱坠落冲击载荷作用下结构的动态特性。
1 典型坠物事故场景
在使用吊机装卸集装箱的过程中,由于吊装设备以及人员操作等原因,常常发生集装箱坠落事故。图1为集装箱吊装场景示意图,其中a、b、c处可能发生缆绳断开以及挂钩的损坏,导致集装箱坠落于甲板。本文坠物选取典型的20尺标准集装箱,其几何尺寸为2.18 m×2.13 m×5.69 m,质量为17.5 t(配货毛重),选取其坠落于甲板的事故场景进行分析。

图1 集装箱吊装场景示意图Fig.1 Schematic diagram of container hoisting scenario
针对集装箱不同坠落状态,选定集装箱与甲板线接触和面接触两种坠落工况,并根据表1甲板板架结构参数,制定如图2所示的两种工况下集装箱坠落场景。其中,基于实际坠落概率选取面接触坠落高度为10 m的工况,即集装箱面接触甲板时的速度约为14 m/s,接触区域为甲板板、纵骨以及横梁的交叉结构;由于接触面积小的线接触工况在低速情况下就可以对甲板造成足够大的损伤,因此选取线接触坠落高度为5 m的工况,而集装箱最低点与甲板的距离小于5 m,所以线接触坠落时集装箱接触甲板的速度约为5 m/s,接触区域为甲板与三根纵骨的交叉结构。

表1 甲板板架结构参数


(a) 面接触坠落

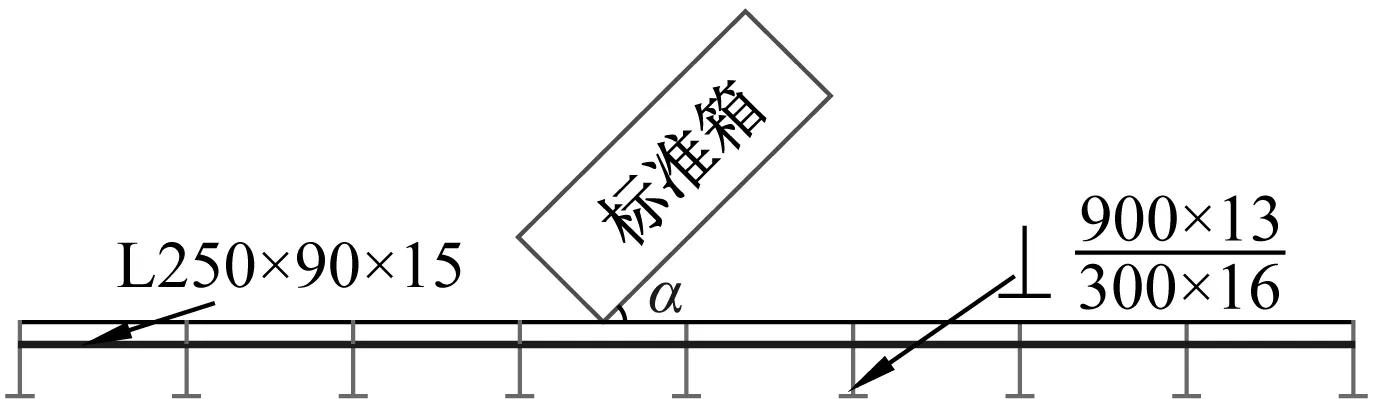
(b) 线接触坠落图2 集装箱坠落场景示意图Fig.2 Schematic diagram of container drop scenarios
2 集装箱坠落载荷作用下板架结构响应理论预报方法
基于仿真计算确定结构损伤变形特征,建立在集装箱坠落时板架结构各组件变形损伤简化模型,在此基础上,运用塑性力学理论,推导得到甲板板、纵骨、横梁的吸能以及撞击载荷计算公式。
2.1 结构损伤变形模式
2.1.1 有限元模型
根据集装箱与甲板结构参数,在有限元软件ABQUAS中建立有限元模型(图3),其中,坐标原点选择甲板中心位置,x轴沿船长方向、y轴沿船宽方向、z轴为垂直方向,集装箱与甲板板、横梁、纵骨采用四边形减缩积分单元(S4R),网格特征长度为80 mm。对于板架结构,其四周刚性约束,即:Ux=Uy=Uz=URx=URy=URz=0,而集装箱仅放松z方向平动自由度,即:Ux=Uy=URx=URy=URz=0。由于重点研究甲板板架结构损伤,其集装箱相对刚度较大,故将其简化为刚体。甲板板架结构使用理想弹塑性材料,密度为7 850 kg/m3,弹性模量为210 GPa,泊松比为0.3,屈服应力为235 MPa,失效应变取0.3[19],摩擦因数为0.3。
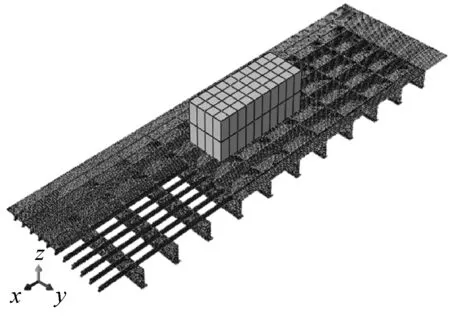
(a) 面接触

(b) 线接触图3 有限元模型Fig.3 Finite element models
2.1.2 仿真结果损伤变形
冲击载荷造成甲板结构的损伤变形集中在接触区域(图4),面接触碰撞区域包含纵骨、甲板以及横梁结构,而线接触坠落主要为甲板以及甲板下方的三根纵骨。

(a) 面接触
(1) 甲板板
图4(a)为面接触板架结构的变形图,甲板上矩形区域产生凹陷变形,在碰撞初期,随着撞深的增加,产生凹陷变形的区域迅速扩大直至扩展到外侧横梁以及外侧纵骨处,塑性铰线的长度基本固定。
图4(b)为线接触板架结构的变形图,甲板上矩形区域产生凹陷变形,在碰撞初期,随着撞击深度的增加,凹陷变形区域不断扩大;随着撞深继续增大,由于横梁结构刚度大,不易产生变形,产生凹陷变形的区域扩大到横梁处,而平行于接触边方向的变形不断扩大并终止于外侧纵骨处。
(2) 纵骨
面接触坠落工况纵骨的损伤变形结果图5(a)与甲板变形结果类似,接触区域有整体向下的位移,在集装箱的边缘以及靠近横梁位置处产生塑性铰,由于纵骨损伤部分长,并且纵骨凹陷部分有多根横梁支撑,纵骨在向下产生凹陷变形过程中并未产生侧向的变形。
线接触坠落工况纵骨的损伤变形结果图5(b)也与甲板变形类似,横梁结构较强,对纵骨的约束近似于固支,纵骨的变形接近于梁的三点弯试验结果,在靠近横梁位置以及与集装箱的接触区域产生塑性铰。
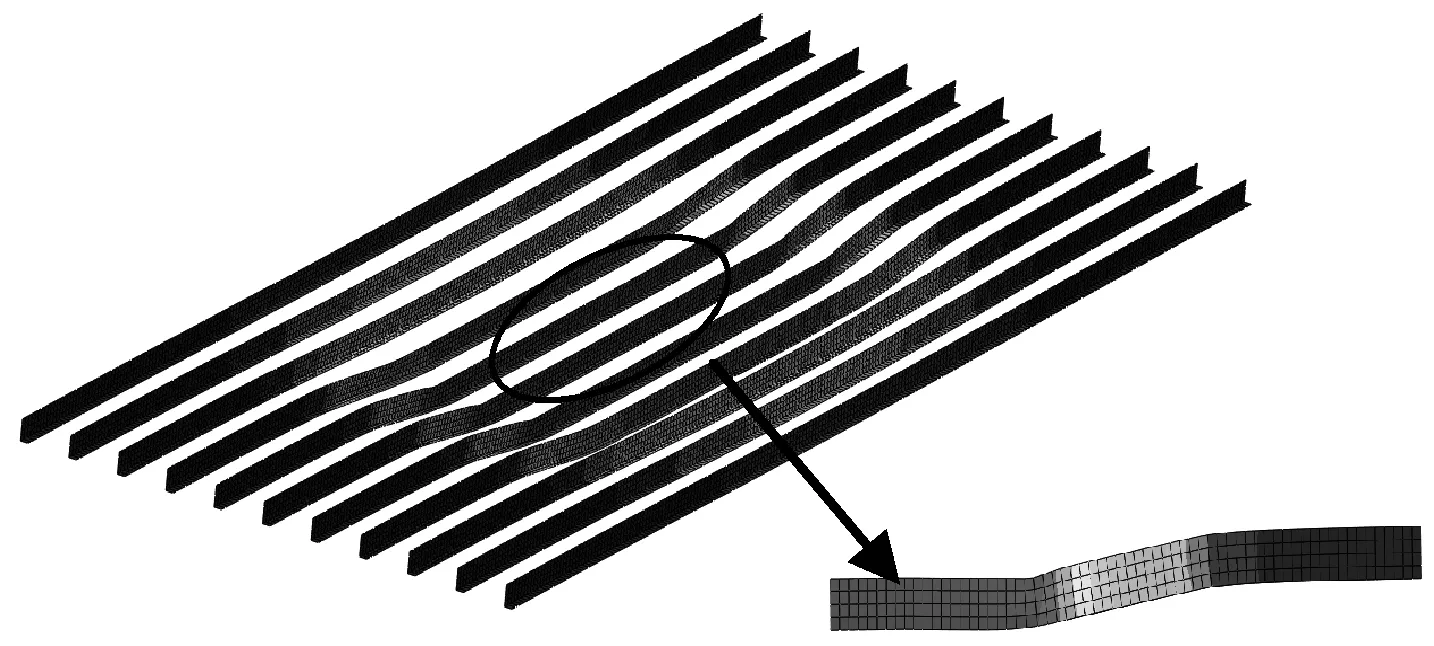
(a) 面接触
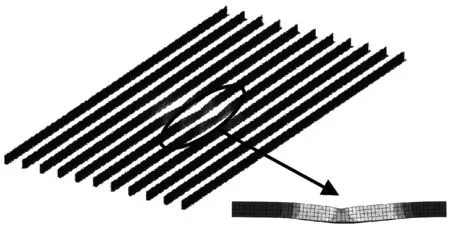
(b) 线接触图5 纵骨损伤变形图Fig.5 Damage and deformation of deck longitudinals
(3) 横梁
横梁的损伤变形结果如图6所示,横梁产生类似于纵骨的变形,由于横梁为T型材,截面为对称图形,在凹陷变形时不会产生侧向变形。
2.1.3 结构变形模式—面接触坠落
(1) 甲板板
在集装箱坠落冲击下,甲板板的变形受到纵骨与横梁的限制,甲板板产生梯台形的凹陷变形,示意图如图7所示。
图7中所取甲板板变形范围定义如下:集装箱底面宽度表示为2a,长度表示为2b,产生凹陷变形的区域长度为2l1,宽度为2l2,δ则为标准箱在垂直于甲板板方向上的撞深。

图6 横梁损伤变形图Fig.6 Damage and deformation of deck beam
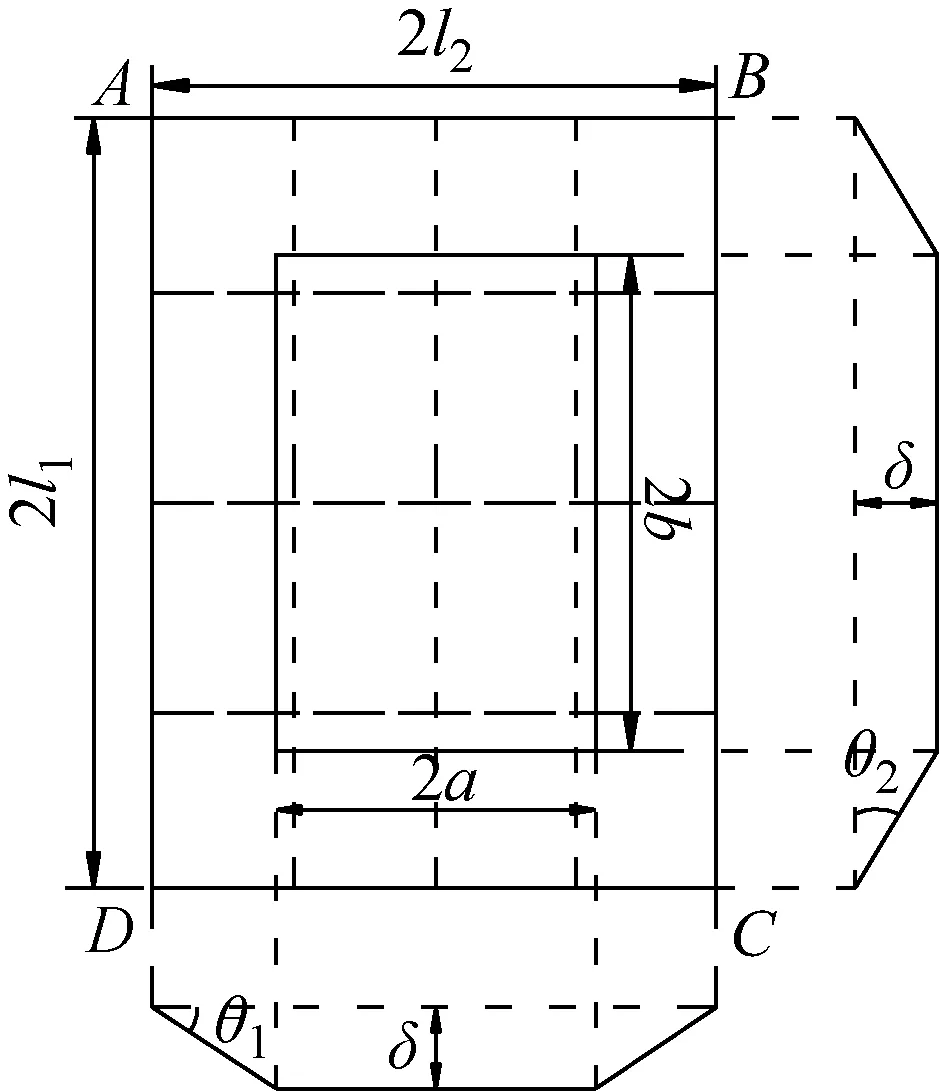
图7 甲板板损伤变形模型Fig.7 Deformation mode of deck plate
所以θ1、θ2依据图7有如下关系
(1)
甲板板在集装箱冲击下,在接触区域产生四条塑性铰线,在外侧纵骨与横梁的约束位置也会形成四条塑性铰线,甲板主要通过凹陷部分的膜拉伸变形以及八条塑性铰线的转动吸能。
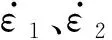
(2)
及
(3)
解得
(4)
及
(5)
又因为单位长度塑性铰线弯矩M0为
(6)
综上可得标准集装箱坠落时甲板板总能量耗散率为
(7)
甲板板的碰撞力表示为
(8)
(2) 纵骨及横梁
由结构的损伤变形简化得到图8中纵骨与横梁的简化变形模式,在一条纵骨或者横梁上会产生四处塑性铰,并在凹陷部分产生膜拉伸变形。由于各单个构件具有相同变形模式,故对单个构件的损伤机理进行分析。

(a) 纵骨

(b) 横梁图8 纵骨与横梁损伤变形模型Fig.8 Deformation modes of longitudinal and beam
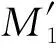
对塑性铰弯矩进行计算,以M1与M2为例,计算过程如下
对于弯矩M1,由于横梁对纵骨变形的约束近似于固定支撑,因此计算M1时假设形心所在平面不因θ角的变化而产生应变。定义面板中面与形心距离为l′,根据形心的定义计算得到
(9)
故有M1为
(10)
式中:lf为纵骨腹板的宽度;tf为对应腹板厚度;ly为纵骨面板的宽度;ty为厚度;σ0为屈服应力表示。
对于弯矩M2,在撞深不断增加的过程中,θ2角也不断增大,但纵骨与压痕的接触位置不会因θ2角的增加而产生应变,对图9中的N点求得弯矩M2为
(11)
图9 纵骨剖面示意图Fig.9 Section profile of longitudinal
此外,依图7可得膜拉伸能量耗散率[20]为
(12)
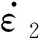
(13)
在集装箱棱线以下有k根纵骨时,所有纵骨的能量耗散率为
(14)
k根纵骨的碰撞力表示为
(15)
于是,同理,对于横梁有:
(16)
(17)
膜拉伸能量耗散率为
(18)

(19)
一般地,当箱体撞击板架时,箱面与板架接触面有k根横梁时,则k根横梁总的能量耗散率为
(20)
k根横梁的碰撞力表示为
(21)
2.1.4 结构变形模式—线接触坠落
(1) 甲板板
由于甲板在集装箱的冲击下变形受到纵骨与横梁的约束,因此甲板产生如图10的变形模式。
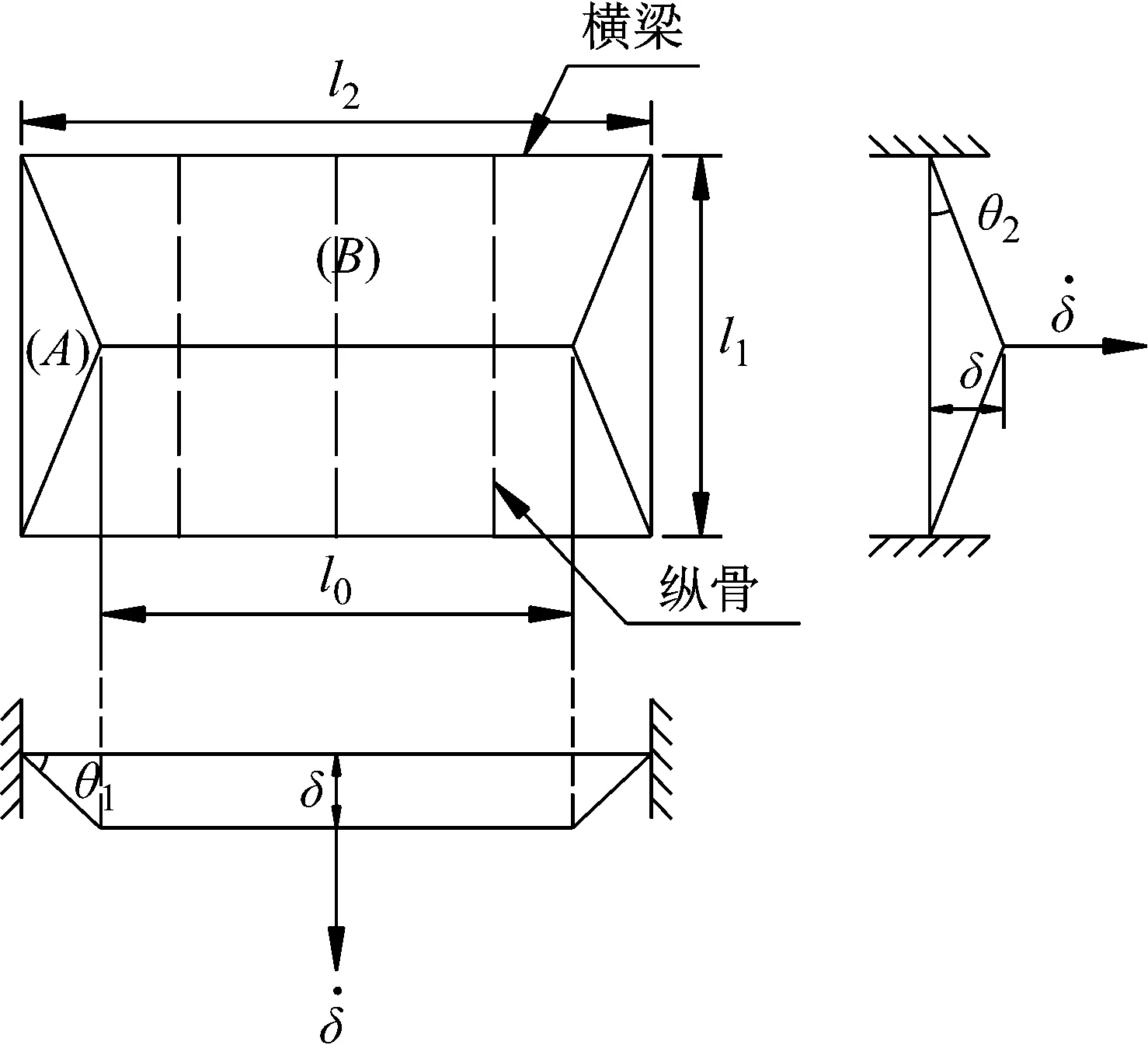
图10 甲板板损伤变形模型Fig.10 Deformation mode of deck plate
图10中所取甲板板面积范围定义如下:l1为横梁间距,l2表示棱线外侧相邻两根纵骨间距。l0为标准箱坠落在甲板板上的棱线长,δ则为标准箱在甲板板纵向的撞深。
所以θ1、θ2依据图10有如下关系
(22)
甲板板在冲击作用下,由于甲板板的凹陷变形,在接触位置以及变形甲板板格四周形成多条塑性铰线,甲板主要通过凹陷部分的膜拉伸变形(接触线两边与原平面产生夹角θ1的梯形区域,平行于接触线方向的三角形区域)以及塑性铰线(斜边与原平面夹角θ1、θ2处以及接触线处)的转动吸收能量。
(23)
及
(24)
解得:
(25)
及
(26)
又因为单位长度塑性铰线弯矩M0为
(27)
塑性铰线主要为接触线部分、凹陷甲板与两边横梁连接的部分和凹陷甲板与两边未变形纵骨连接部分,则变形区域内塑性铰能量耗散为
(28)
凹陷甲板梯形区域A与三角形区域B膜拉伸能量耗散为
(29)
综上可得标准箱线接触坠落时甲板板总能量耗散率为
(30)
甲板的碰撞力表示为
(31)
(2) 纵骨
由于在该坠落场景中集装箱边线一直处于水平状态向下平移,集装箱的边同时作用于多条纵骨上,并且纵骨的变形情况类似,故仅选取一根纵骨进行分析。依据仿真结果将纵骨的变形进行简化,变形模式如图11所示。

图11 纵骨损伤变形模型Fig.11 Deformation mode of longitudinal
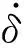
与前述面接触坠落中纵骨及横梁变形同理,对于M1,需对其固支截面中心取矩;对M2,需对截面中心上端顶点取矩,因此同理可得下式
(32)
(33)
(34)
此外,依图10可得膜拉伸能量耗散率为
(35)
所以可得单根纵骨总的能量耗散率为
(36)
在集装箱棱线以下有k根纵骨时,所有纵骨的能量耗散率为
(37)
k根纵骨的碰撞力表示为
(38)
3 坠物载荷下甲板板架结构响应分析
针对集装箱不同坠落状态,通过上一部分推导的结构变形模式,对集装箱与甲板线接触和面接触时结构损伤变形情况进行分析,并通过与有限元仿真结果进行对比,以验证本文预报方法的可行性。
3.1 撞击载荷
图12为集装箱坠落时的碰撞力曲线对比图,撞深较小时两工况的载荷迅速上升达到弹性极限,曲线的趋势较为一致,弹性极限后,仿真值出现波动,而解析值较为平缓,这是由于解析时对结构变形的简化,使得解析结果得到的碰撞力曲线较为平缓,忽略了结构失稳导致承载力迅速下降的过程,但解析结果在碰撞力均值上有一定准确性。
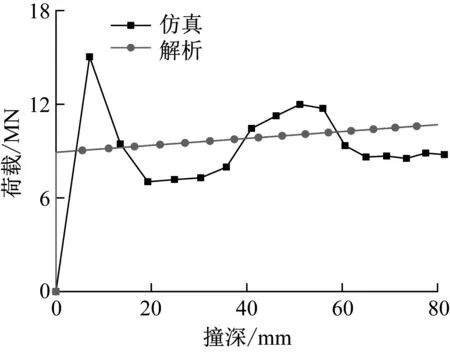
(a) 面接触
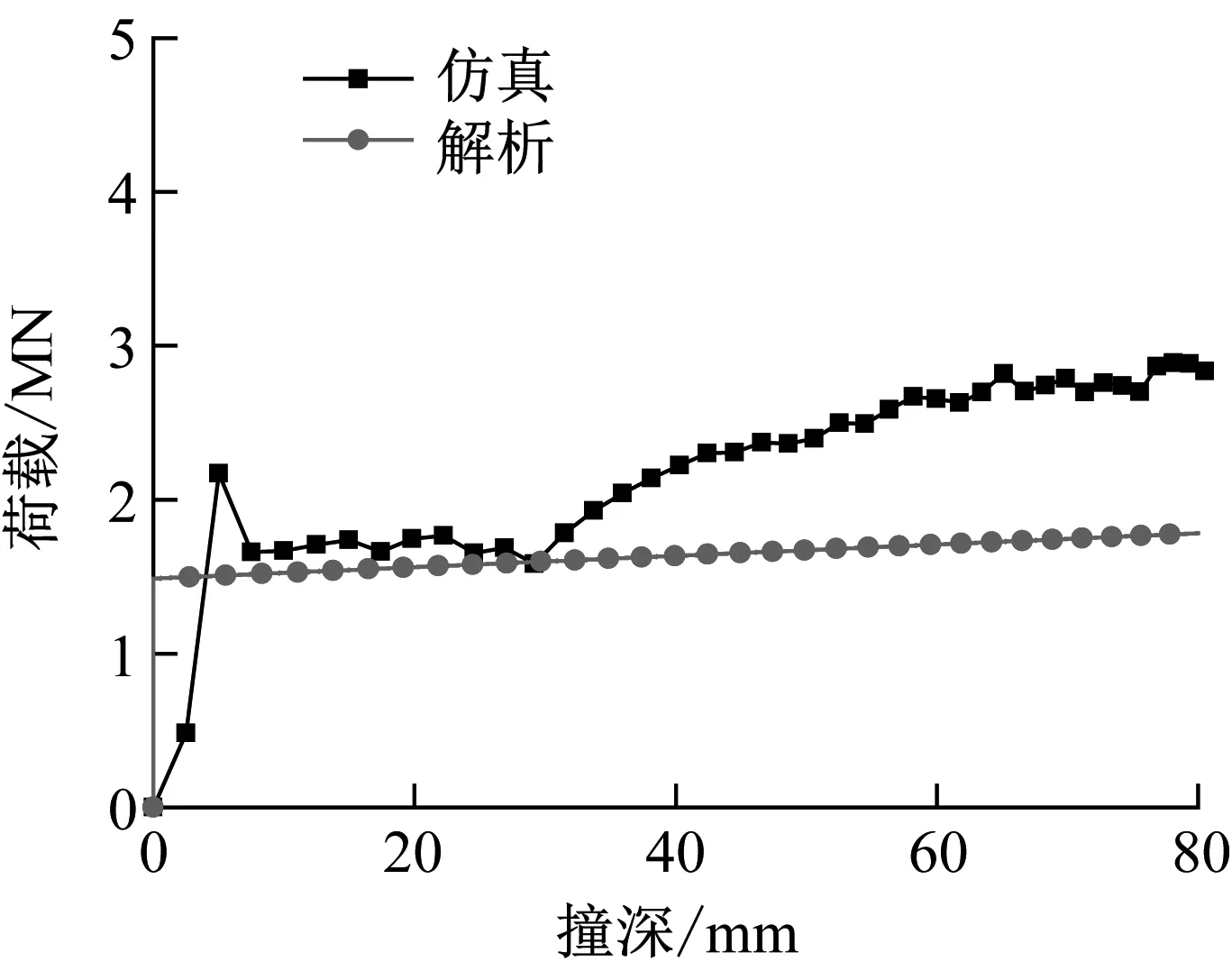
(b) 线接触图12 碰撞力比较Fig.12 Comparison of collision forces
3.2 能量吸收
3.2.1 面接触坠落
图13(a)为集装箱以面接触形式坠落时的各结构吸能曲线对比,图中可以看出:甲板板与总能量的解析结果与仿真结果吻合较好;纵骨在撞深较小时仿真与解析结果相差较大,产生较大误差的原因是在碰撞初始阶段,纵骨的腹板会产生一段压缩变形,在对纵骨吸能开展解析计算时不便与塑性铰转动一同考虑,导致解析结果相比有限元结果小,随着塑性铰的产生,纵骨腹板的压缩变形逐渐消失,而此时纵骨两侧膜拉伸变形逐渐成为主要吸能要素,解析值不断接近仿真结果。横梁解析结果在撞击初期较小,而后略大于仿真结果,造成这一现象的原因是仿真中横梁高大的腹板在瞬时冲击过程中产生局部变形,仿真结果偏大,而后整个腹板发生弯曲,由于横梁中间截面腹板被压溃,在撞深继续增加时,整体产生膜拉伸变形的应变率显著下降,吸能效率有所下降,故结果有一定差异。
3.2.2 线接触坠落
图14为集装箱线接触形式坠落时各结构吸能曲线对比。从曲线图可以看出,仿真结果与解析结果整体吻合较好。甲板板吸能曲线在碰撞初期结果相差较大,主要原因是在碰撞初期,甲板板吸能仿真结果远大于解析结果,在撞深增加后,仿真结果增加减缓,与解析结果的差距逐渐减小;这是由于在碰撞初期,标准箱与甲板的接触面积较小,产生塑性变形的区域不断向外扩大,在一定时间后才会扩展到横梁处,而解析中假设的塑性变形范围一直是棱线下方的5块板格,因此在解析计算时会产生一定误差;在撞深比较大时,凹陷范围已经扩展到横梁处,解析与仿真结果趋势较为一致。而纵骨解析结果在撞击初期较小,而后略大于仿真结果,造成这一现象的原因与面接触工况中横梁解析结果出现这一现象的原因相同。
通过对比分析,总体来说解析结果与有限元仿真结果基本吻合,验证了本文理论预报方法对板架结构的吸能解析结果具有一定适用性和合理性。
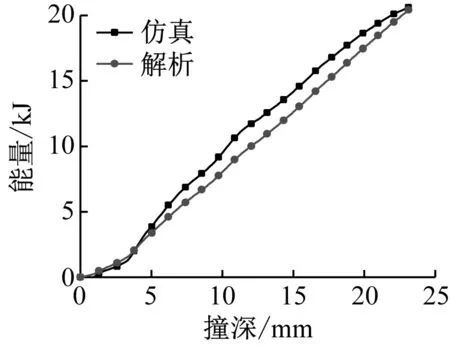
(a) 甲板板
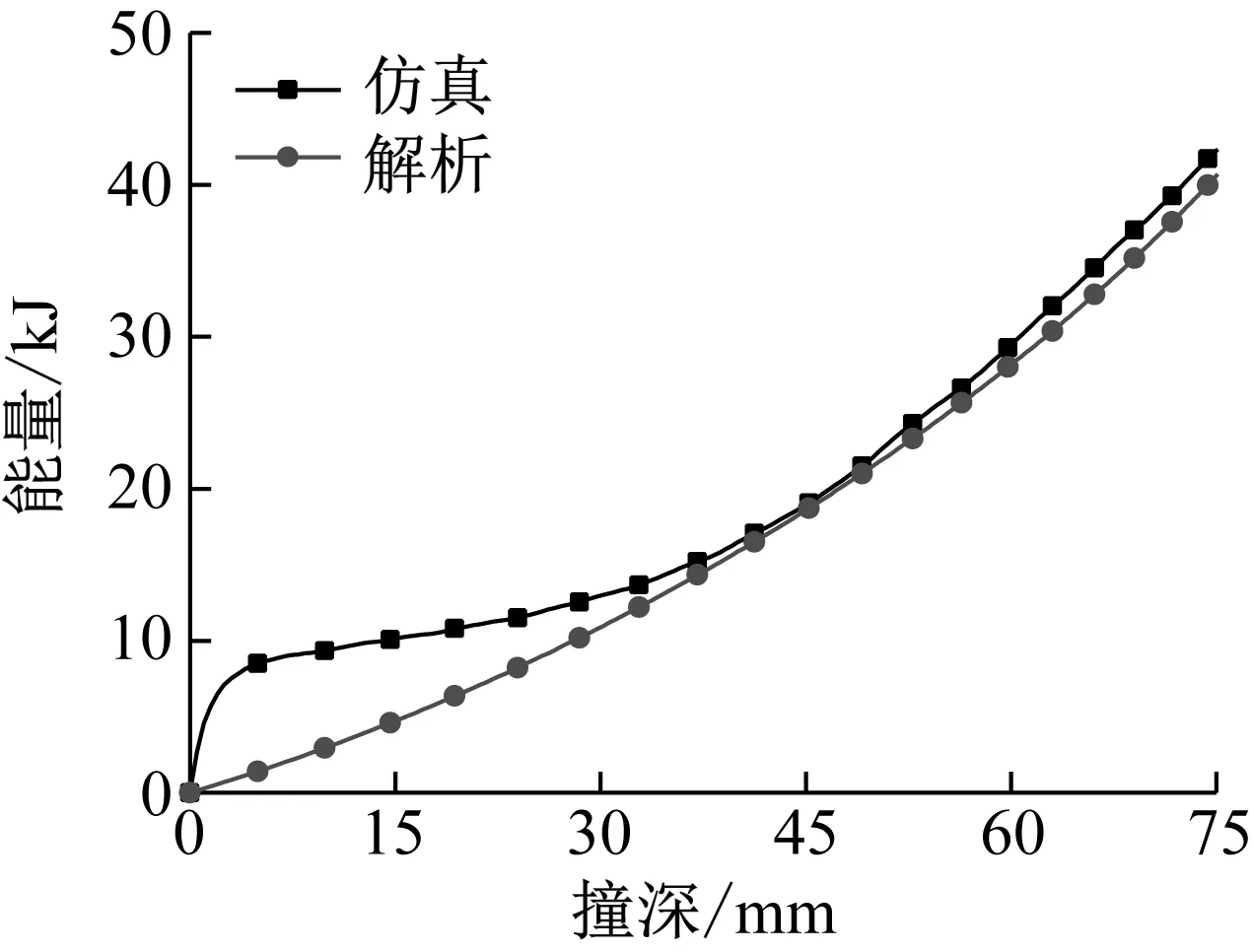
(a) 甲板板
4 结 论
本文以典型船体板架结构为研究对象,开展标准集装箱的坠落冲击有限元计算,通过分析甲板板架各组件的损伤变形简化得到其变形模式,运用塑性力学基本理论开展解析计算研究。主要结论如下:
(1) 在集装箱面接触坠落工况中,甲板板架中纵骨与横梁为主要吸能构件,且此类强结构的尺寸以及间距对吸能影响明显;在线接触坠落工况中,纵骨为主要吸能构件,在结构设计时,纵骨的尺寸以及分布对板架结构的耐撞性具有很大的影响。因此在结构设计阶段需考虑这些特点。
(2) 依据标准箱面接触以及线接触形式坠落工况建立板架结构的塑性变形理论模型,并推导了各构件的能量耗散率计算公式,与仿真结果对比证明该方法有一定的准确性,可用于板架结构耐撞设计的快速评估。
(3) 本文通过运用塑性力学理论建立了理论预报方法,适用于快速评估箱型坠物坠落于甲板板上时甲板板的抗撞性能以及甲板板架结构抗撞设计。

