基于总场公式的水下冲击结构响应分析方法

张 浩，赵梓斌，李上明,2

(1. 中国工程物理研究院总体工程研究所，四川，绵阳 621999；2. 工程材料与结构冲击振动四川省重点实验室，四川，绵阳 621999)

对于水下冲击结构响应问题而言，准确地模拟水下冲击波作用在结构上的载荷是影响计算结果合理性的关键之一。在这类流固耦合问题中，水下结构满足连续介质条件，使用有限元方法离散，而水下结构周围的流体域则满足无限声学水域条件，当作无粘无旋的理想流体即声学波动介质处理。通过将有限元方程与模拟无限流域的方程耦合，用于分析无限流域下的结构冲击响应问题。

模拟无限流域常用的方法是通过无限域截断边界，将无限域截断成有限域，在截断边界上施加能准确反映无限水域动力特性的边界条件或单元，无反射边界条件和无限元法就是常用的方法之一，在有限元商用软件如ABAQUS、ANSYS、LS-DYNA 等都能找到其应用方法。采用有限元商用软件中的无反射边界条件或无限元法时，为得到合理准确的计算结果，有限域的离散场要求较大，无限流域的截断边界半径通常要求是分析结构半径的6 倍或以上[1]。这就意味着当结构模型较大时，有限流域的离散场将会占据较多的计算资源，使分析规模增大。

本文提出的水下冲击结构响应的总场公式是基于分离场技术[2]，在不考虑空化作用条件下，将总场冲击波压力分解为散射场压力和自由场压力，自由场压力由经验公式计算，避免了计算冲击波在流体中传播的过程，降低了分析规模。将可用于反映无限水域动力特性的PWA 总场公式和SBFEM 总场公式，分别与流固耦合系统的FEM方程耦合，建立PWA-FEM 总场公式和SBFEMFEM 总场公式。PWA 方程是一种高频端渐近式[3]，可以用于求解早期高频响应，而中后期响应与DAA方法[4]相比精确度有所欠缺。但由于其表达式简单，易于和FEM 方程耦合，所以有一定的工程应用价值[5]。而SBFEM[6]作为一种较新的半解析解方法，在径向方向即离散面法向方向的解是精确解，严格满足无穷远处边界条件，已成功应用于无限水库[7]和无限岩土[8]模拟，也可与有限元商业软件联合使用[9]，能准确的模拟无限域问题[10]。Zhao 等[11]使用基于SBFEM 的修正高阶透射边界来模拟无限域，证明了总场公式的有效性，许贺等[12]提出了一种基于FEM-SBFEM 的坝-库水动力耦合简化分析方法，Yaseri 等[13]使用SBFEM-FEM 模拟土坝-弹性峡谷系统，计算了不同形状的无限大弹性峡谷对土坝-弹性峡谷系统固有周期的影响，SBFEM 还可用于土-结构相互作用系统中无限地基的模拟[14-15]。SBFEM 方程对于减小无限域问题的有限域离散半径有重要意义，降低了分析规模，并且SBFEM 方程模拟无限域问题时，对边界形状要求不高，可适用范围更广。

1 声固耦合系统的FEM 方程

对于图1 所示的含有无限水域的水下结构声固耦合系统，其中无限水域被截断边界S 分成有限水域和无限水域，并且声学水域满足声学波动方程：

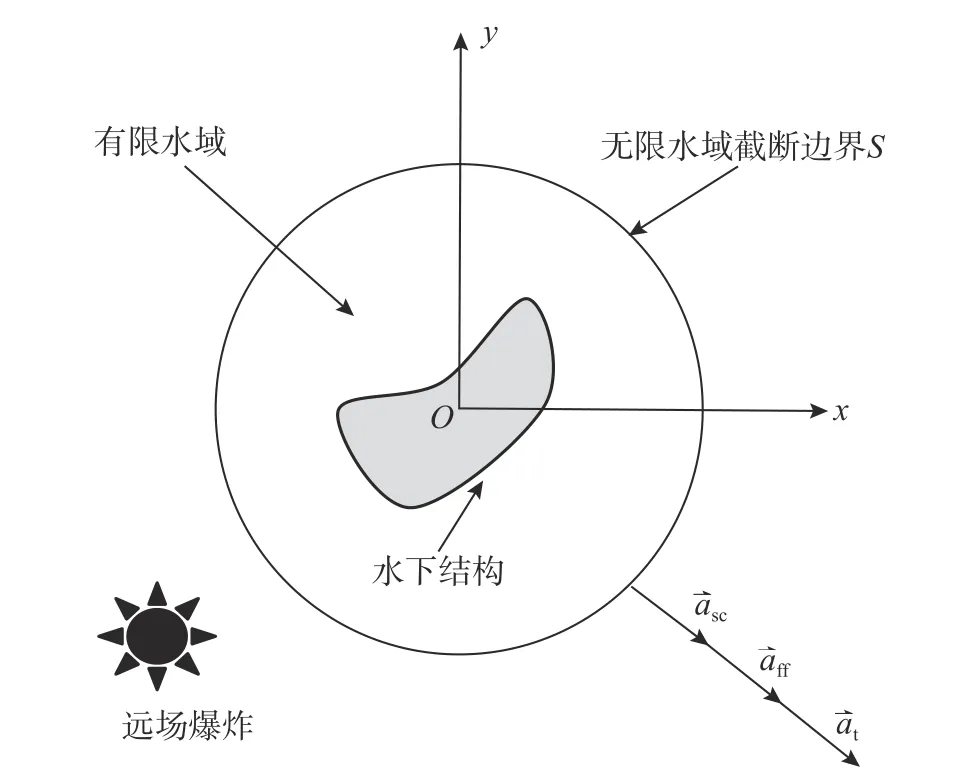
图1 声固耦合系统Fig. 1 Acoustic fluid-structure coupling system

对于无限水域截断边界以内的水下结构与有限水域的声固耦合系统，其有限元耦合方程可写为：

2 无限水域PWA-FEM 总场公式

根据平面波近似理论[3]，压力和流体质点速度的关系如下：

式中：P为流场压力； ρ为流体密度；c为流场中声速；V为流体质点速度。

对于图1 所示的声固耦合系统，流场经由截断边界S分割成有限域和无限域，无限域的动力特性通过截断边界S上的PWA 方程描述。

在无限水域截断边界S上，无限域散射场压力Psc和等效加速度a′sc之间关系由式(8)求导后得出：

式(23)为含冲击波载荷的水下结构声固系统的全耦合方程，该公式可以用Newmark 法进行求解。

3 无限水域SBFEM-FEM 总场公式

采用SBFEM 模拟图1 所示无限水域，根据SBFEM 理论，只需无限水域截断边界S，离散模型见图2，即截断边界上的任意单元i 和j 具有相同的相似中心O，整个无限水域的动力特性通过截断边界上的SBFEM 控制方程描述。

图2 无限水域SBFEM 离散模型Fig. 2 SBFEM discretization of infinite fluid

式(53)即为含冲击波载荷的SBFEM-FEM 总场公式。该公式可采用Newmark 法进行求解分析无限水域下的结构冲击响应问题。

以上两种总场公式的推导，均与冲击波载荷衰减形式无关，在已知自由场冲击波压力和流体加速度的情况下，即可进行求解。

4 算例

分别使用PWA-FEM 总场公式和SBFEM-FEM总场公式，对浸没在无限水域中、受平面波冲击作用的无限长圆筒[17]进行线性瞬态响应分析，来验证总场公式的可行性和合理性，其示意图见图3，而其有限元模型见图4。

图3 平面冲击波与水下圆筒Fig. 3 Plane shock wave and submerged cylindrical shell

图4 水下圆筒与离散水域有限元模型Fig. 4 FE model of submerged cylindrical shell and discretised water domain

图5 给 出 的是 β=0 (冲 击波 不 衰减)、 θ=0°、90°和 180°处，圆 筒平均半径r处 法向速度vn。θ为圆筒外法线与水平轴线的夹角。图中横坐标和纵坐标均为无量纲量，无量纲速度为vn/c，无量纲时间为ct/r，t为时间。

图5 R/r=4 时PWA-FEM 解与Huang 的解析解和数值解的比较Fig. 5 Comparison of PWA-FEM solution with Huang's analytical solution and numerical solution when R/r=4

采用PWA-FEM 总场公式对圆筒算例进行计算分析，无限域圆形截断边界半径取圆筒结构半径的4 倍，见图4，流场环向单元分别取40 个、80 个、120 个，流场径向单元取100 个，圆筒环向单元与流体域相同，径向单元取2。圆筒用四节点平面应变单元离散，有限水域用四节点平面声学单元离散，无限水域用截断边界上的PWA 总场公式模拟。图5给出的是基于PWA-FEM 总场公式的数值解、Huang[19]的级数解析解和采用无反射边界条件计算的数值解。数值解采用的是三维模型，水下圆筒用C3D8R 单元离散，有限流域用A3D8R 单元离散，径向模型网格参数与PWAFEM 总场公式设置相同，轴向单元数设置为1，轴向厚度设为0.01，无限流域通过在无限流域截断边界设置Planar 型无反射边界条件模拟，流固耦合面用Tie 连接，分别采用total wave 公式和scattered wave公式计算。

从图5 可以看到，在有限域取结构半径4 倍的条件下，PWA-FEM 总场公式的计算结果与解析解、总波解和散波解吻合较好，随着流场环向单元数的增加，PWA-FEM 总场公式的计算结果逐渐收敛于解析解、总波解和散波解。PWA-FEM 总场公式在环向单元较少时无法准确模拟无限流域，而随着环向单元的增加，模拟的准确度也随之增加，并逼近于解析解、总波解和散波解。这说明了PWA-FEM 总场公式模拟无限流域有一定的合理性和可信度。

图5 中的PWA-FEM,K=40,R/r=4 计算曲线出现了较大波动，为探究该现象发生的内在机理原因，提取了圆筒算例的流固耦合面上 θ=0处的声学流体总压进行分析，计算结果见图6。

图6 R/r=4 时，流固耦合面上 θ=0处的声学流体总压Fig. 6 Acoustic fluid total pressure of fluid-structure interaction at θ =0 when R/r=4

从图6 可以看出，在无限域截断半径不变的条件下，环向单元数K=40 时，流固耦合面上θ=0处的声学流体总压是振荡变化的，但总体呈稳定变化趋势。图6 的PWA-FEM,K=40,R/r=4 计算曲线出现误差的原因是PWA-FEM 总场公式的环向单元数较少，流体有限元网格过大，随着网格加密，计算结果逐步收敛。

图7 是在环向单元数取120 时，取不同无限流域截断半径条件下的计算结果。从计算结果可看出，在环向单元数不变的条件下，随着有限流域半径的增加，计算结果也逐渐收敛于解析解、总波解和散波解。这说明了使用PWA-FEM 总场公式模拟无限流域时，仍需要较大的有限域才能准确的模拟无限域。

图7 中可以明显看出，PWA-FEM,R/r=2.2,K=120 的计算曲线在无量纲时间ct/r=4～5 范围内出现较大误差，为进一步探究该误差出现的内在机理原因，提取了圆筒算例的流固耦合面上 θ=π处的声学流体总压进行分析，计算结果见图8。

图7 K=120 时PWA-FEM 解与Huang 的解析解和数值解的比较Fig. 7 Comparison of PWA-FEM solution with Huang's analytical solution and numerical solution when K=120

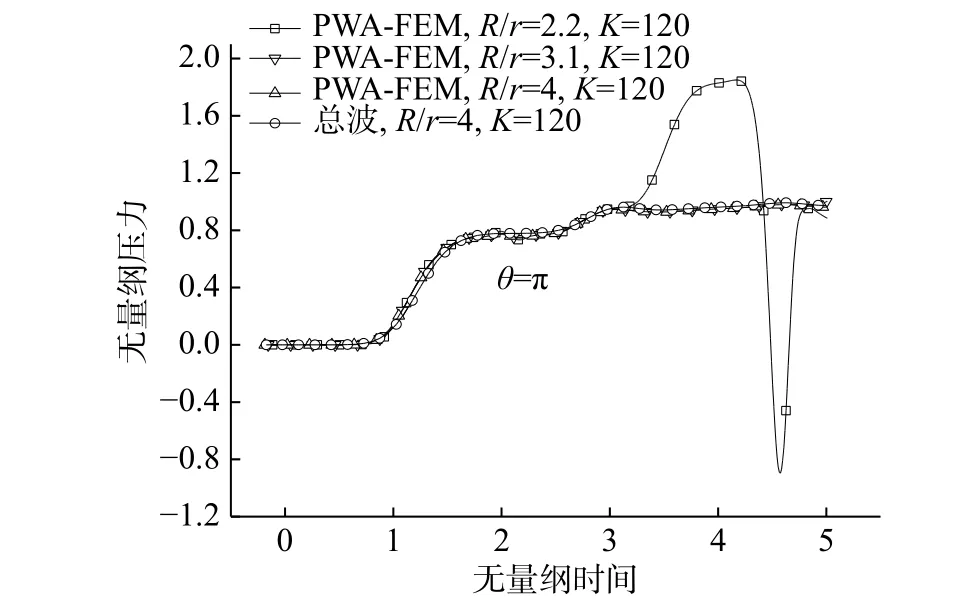
图8 K=120 时，流固耦合面上 θ=π处的声学流体总压Fig. 8 acoustic fluid total pressure of fluid-structure interaction at θ=π when K=120

图8 是在环向单元数等于120，取不同无限流域截断半径条件下，流固耦合面上 θ=π处的声学流体总压。从图中可以看出，在无限流域截断半径较小时，PWA-FEM 求解的压力在后期计算中出现了较大波动，而在无限流域截断半径较大时，PWA-FEM 求解的总压与ABAQUS 总波公式计算的结果非常吻合。出现这种现象的原因是有限流域较小时，PWA-FEM 总场公式对边界的吸收特性未能准确的模拟，导致了部分散射波在边界反射重新进入计算域，进而使流体总压出现较大波动，所以图7 中PWA-FEM,R/r=2.2,K=120 计算曲线在无量纲时间ct/r=4～5 范围内会出现较大误差。

图9 给出了SBFEM-FEM 总场公式对该算例进行模拟计算的结果。与PWA-FEM 总场公式、常规有限元方法相比，用SBFEM 模拟无限水域时，能大大减小无限水域截断边界的半径，减少有限域单元数量和计算规模。

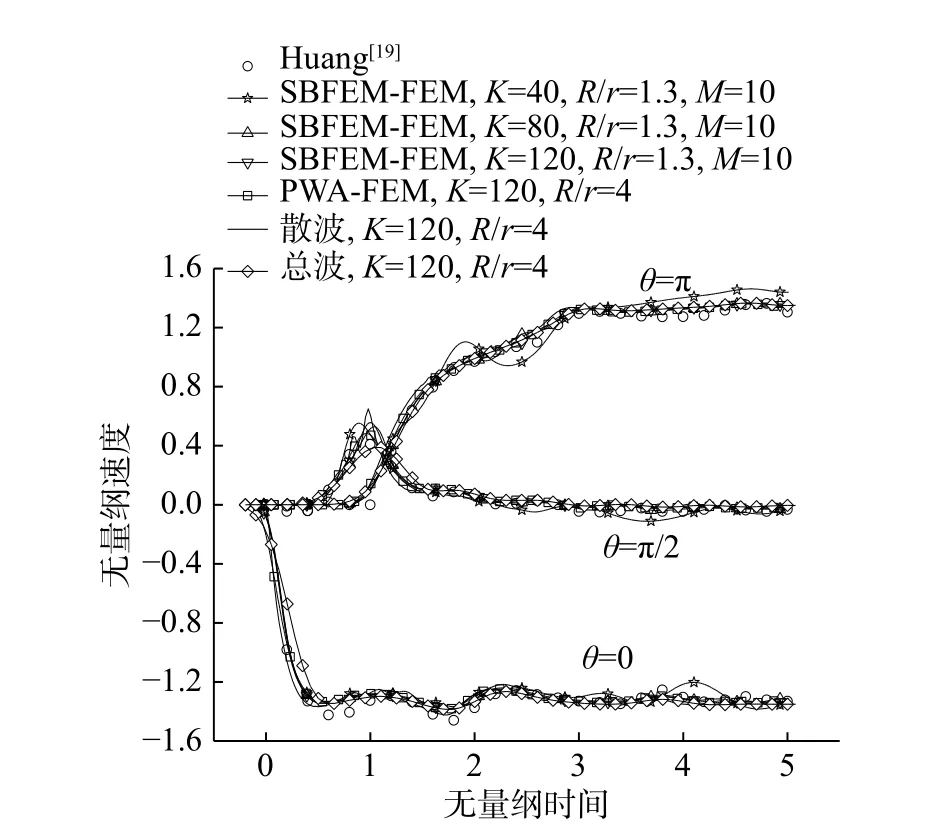
图9 R/r=1.3 时SBFEM-FEM 解与Huang 的解析解、数值解和PWA-FEM 解的比较Fig. 9 Comparison of SBFEM-FEM solution with Huang's analytical solution , numerical solution and PWA-FEM solution when R/r=4

从图9 可以看出，在环向单元数K=40 时，SBFEM-FEM 总场公式的计算结果与解析解相比，出现了部分偏差，而在环向单元数K逐渐增加到80 和120 后，SBFEM-FEM 总场公式的计算结果收敛于解析解和数值解，说明了SBFEM-FEM总场公式模拟无限水域的合理性和可靠性，且收敛速度要快于PWA-FEM 总场公式；此外，在环向单元数K=120 的情况下，SBFEM-FEM 总场公式计算结果与PWA-FEM 总场公式计算结果基本一致时，所需要的无限流域截断边界半径明显小于PWA-FEM 总场公式，说明了SBFEM-FEM 总场公式可有效减小无限流域截断边界半径，减小有限域离散范围和单元网格数量，减小了分析规模。

现将数值算例的圆形截断边界改为矩形截断边界时，系统模型如图10 所示，以便考察PWAFEM 和SBFEM-FEM 总场公式对其他边界形状的适应性。

图10 水下圆筒与矩形边界Fig. 10 Underwater cylinder and rectangular boundary

图11 是矩形截断边界条件下，PWA-FEM 总场公式和SBFEM 总场公式的计算结果。在截断边界为方形、环向单元数K=120 的条件下，SBFEMFEM 总场公式的计算结果一定程度上优于PWAFEM 总场公式，与圆形边界相比结果相差不大。总体看，文中给出的两类总场公式均能适应不同边界形状。

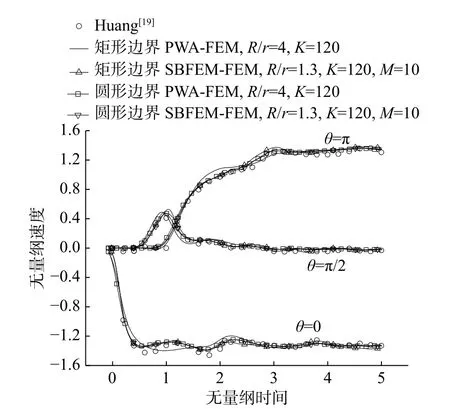
图11 不同边界形状的计算结果对比Fig. 11 Comparison of calculation results of different boundary shapes

5 结论

本文基于分离场技术提出的总场公式理论具有以下特点：

(1) PWA-FEM 和SBFEM-FEM 总场公式均可用来模拟冲击波作用下的含无限水域的结构冲击响应问题，该公式将冲击波载荷等效成截断边界上的等效节点力，简化了冲击波传播的模拟过程；

(2) SBFEM-FEM 总场公式因其继承了SBFEM半解析的特点，即在径向方向(指向无穷远的方向)的解精确满足能量吸收性，故模拟无限流域问题时，可取较小的截断半径；

(3) PWA-FEM 总场公式形式简单，易编程实现，计算效率较高，但其无限水域的离散域相对较大，建议取水下结构长度的3 倍左右；

(4) 当前两类方法均可适用于任意形状边界的无反射特性的模拟；

(5) PWA-FEM 和SBFEM-FEM 总场公式在推导和求解过程中与计算结构规模大小无关，在本文中仅用较为简单的小规模算例进行验证，而对于更大规模的真实结构则暂时未进行验证。