强台风下带挑檐双坡低矮房屋风荷载特性大涡模拟方法适用性研究

闫渤文，马晨燕，赵 乐,2，杨庆山,3

(1. 重庆大学土木工程学院，重庆 400044；2. 中机国际工程设计研究院有限责任公司，湖南，长沙 410000；3. 北京交通大学结构风工程与城市风环境北京市重点实验室，北京 100044)

中国是世界上受台风影响最严重的国家之一，尤其是我国东南沿海地区，台风灾害发生频率和影响程度都远大于其他自然灾害。我国沿海地区每年平均约有7 个台风登陆，其中不乏造成了巨大的经济损失和大量人员伤亡的超强台风，例如：“天鸽(201713)”、“山竹(201822)”以及“利奇马(201909)”等。国家减灾委办等部门对2018 年全国自然灾害情况进行了统计分析，核定2018 年台风灾害共造成直接经济损失697.3 亿元，倒塌房屋上万间[1]。其中，由低矮房屋损毁造成的损失占风灾损失的50%以上[2]。因此，开展台风风场下低矮房屋风荷载特性的研究是十分必要和非常亟需的。

20 世纪末，国外学者对常规大气边界层风场作用下的低矮房屋风荷载特性开展了系统的现场实测研究。Eaton 和Mayne[3]搭建了屋面坡度为5°～45°的双坡屋面低矮房屋—艾尔斯伯里实验房(Aylesbury Building)；Richards 等[4]搭建了长度为6 m 的平屋面西尔斯正方形实验房(Silsoes cube Building)；Levitan 和Mehta[5-6]搭建可旋转的屋面坡度为2° 的低矮房屋得克萨斯理工大学实验房(Texas tech university Building, TTU)。近年来，国内外学者逐步开展强台风/飓风作用下的低矮房屋风荷载特征的研究。Masters 等[7-8]和Pita 等[9]基于佛罗里达州海岸监测计划(The florida coastal monitoring program, FCMP)通过移动测风塔对飓风近地面10 m 高度处的平均风场和湍流特性进行研究，并选取了30 座典型低矮房屋作为研究对象，对飓风下低矮房屋的风压实测研究。国内香港城市大学李秋胜等[10-13]在华南沿海区域搭建了移动平屋顶及双坡屋面的低矮房屋，以探究台风近地风场特性及台风风场下低矮建筑屋面的风荷载分布规律。Masters 等[7-8]和李秋胜等[10-13]通过分析阵风因子、湍流度以及湍流积分尺度的变化规律，研究了近地台风风场特性，并与季候风特性进行对比。结果表明：由于台风自身热浮力作用和风向的剧烈变化的影响，台风顺风向、横风向及竖向脉动风速功率谱密度值大于季风的实测值，湍流强度大于季候风的湍流强度，从而导致屋面极值风压系数大于季候风作用下屋面风压系数[12]。

虽然现场实测是获得低矮房屋真实风荷载特性的重要手段，但其需要高额的设备成本和长期的人力投入，且其受到周边复杂实测环境影响，难以开展定量和系统的参数分析和机理研究。因此，在现场实测的基础上，研究者开展了大量的风洞试验：基于Aylesbury Building 的现场实测，Sill 等[14]开展了缩尺比为1∶100 风洞模型对比试验；Cheung 等[15]在澳大利亚莫纳什大学(Monash University)风洞试验室展开了缩尺比为1∶10 TTU模型风洞试验研究；Ham 等[16]在美国科罗拉多州立大学(Colorado state university)风洞试验室开展了缩尺比为1∶50 TTU 模型风洞试验研究；Surry 等[17]利用西安大略大学(University of western ontario)风洞试验室开展了1∶100 缩尺比的TTU 模型风洞试验研究。通过大量风洞试验与实测结果的对比，验证了风洞实验的有效性，且基于此，可以开展大量的参数分析。国内学者聂少锋等[18]考虑了屋面形式、屋面坡度、来流条件及挑檐长度对屋面风压的分布，对低层双坡屋面和四坡屋面开展了风洞试验研究，加强对低矮房屋破坏机理的了解，为结构设计规范提供参考。近年来，结合现场实测，Wang 等[19-20]也开展了缩尺比为1∶50和1∶100 的低矮房屋模型在台风风场下的风洞试验研究。

随着高性能计算资源的飞速发展和高保真数值仿真技术的不断完善，计算流体力学方法(Computational fluid dynamics, CFD)被越来越多地用于研究低矮房屋风荷载特性。目前，根据所采用的湍流模型不同，CFD 数值模拟主要有雷诺平均方法(Reynolds-averaged navier-stokes，RANS)、分离涡模拟(Detached eddy simulation，DES)及大涡模拟方法(LES)。周绪红等[21]和王相军等[22]采用RANS模型研究了低矮房屋表面平均风压分布及变化规律，数值模拟结果与现场实测及风洞试验的结果吻合较好，验证了RANS 模型在模拟低矮房屋屋面平均风压特性的准确性。然而，RANS 模型主要描述时间平均意义上的涡旋运动，在平均风荷载模拟方面效果较好，但对脉动风荷载模拟效果差。而LES 在时间尺度上对湍流的非定常运动进行直接求解，对大于特征网格尺度的涡旋运动直接求解，而小于特征网格尺度的涡旋运动则采用亚格子模型(Sub-grid scale model，SGS)进行模拟，因而克服了RANS 模型无法直接描述非定常流动特性的主要缺陷，不仅可以给出较好的平均风荷载信息，同时也可以给出脉动荷载信息。Nozawa 等[23]运用LES 研究了湍流强度、地面粗糙度等参数对低矮建筑表面风压特性的影响。周晅毅等[24]基于低矮房屋TTU 的风洞试验结果，验证了LES 方法能够模拟大气边界层风场下低矮房屋平均及脉动风压的分布特性。

目前低矮房屋的数值模拟主要考虑大气边界层风场下无挑檐平屋盖低矮建筑的平均风压、脉动风压和点风压谱等的对比验证，尚缺乏对风荷载特性的高阶统计量(偏度、峰度和风压极值等)的验证，且对台风风场下低矮房屋风荷载特性的数值模拟研究也属于空白。因此，本文基于台风“莎莉嘉”和“彩虹”期间带挑檐低矮双坡房屋的现场实测情况及风洞试验情况，采用大涡模拟方法对带挑檐低矮双坡房屋气动荷载特性进行了对比验证，开展了数值模拟与风洞试验结果的定量分析，结合流动显示技术提供的低矮房屋周边瞬态扰流特性，对低矮房屋屋面风荷载分布规律开展了机理研究。

1 研究方法

本文依据带挑檐双坡低矮实测房[12,19]在台风“莎莉嘉”和“彩虹”登陆期间的现场实测结果和风洞试验研究，开展了LES 数值模拟。本节主要介绍了低矮房屋风荷载特性研究采用的现场实测设备、风洞试验方法及数值模拟。

1.1 现场实测和风洞试验

本文采用的现场实测来源于Wang 等[12]在我国海南省文昌县翁田镇沿海海岸建立的实测房，其建筑结构为带挑檐双坡屋面尺寸为24.5 m(长)×9.5 m(宽)×4.4 m(高)，屋面坡度为9.5°，在房屋单侧伸出长度为1.3 m 的挑檐，且挑檐外侧距离地面高度为3.5 m，如图1 所示。现场实测中屋面测压点布置见图2，将测点布置在主导风向一侧。在实测房附近设立一测风塔，在测风塔高度为4 m、7 m、10 m 处分别安装了一台超声风速计用来测量不同高度处的风速及风向。此外，在该测风塔的7 m和10 m 高度处分别安装了YOUNG 式机械式风速仪，用于对超声风速仪结果进行校核和标定。现场实测的风速采样频率为20 Hz。采用可拆卸的压力测量系统进行风压测量，采样频率同样为20 Hz。

图1 实测房立面尺寸图 /mmFig. 1 Cross-section of the instrumented low-rise building

图2 试验模型测点布置图Fig. 2 Arrangement of the pressure taps on the low-rise building roof

式中：U为实测平均风速；u*为切向速度；κ为von Karman 常数；u′、v′、w′分别为顺风向、横风向及竖向脉动风速分量； σw为竖向风速的标准差；下标 avg 为平均值；下标 ind为相应的单个样本值。根据离地面10 m 高度处超声风速仪记录的数据，按照式(1)获得的表面粗糙度z0如表1 所示。在不同的风向角下，地面粗糙度在0.02 m～0.7 m变化。更详细的实测房屋信息可参考文献[12]。

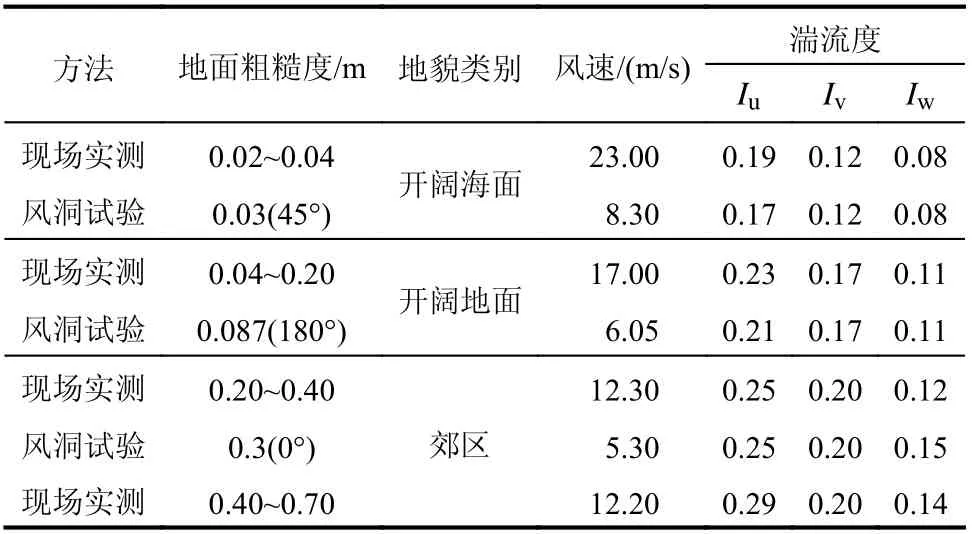
表1 现场实测和风洞试验的风场特性Table 1 Wind field characteristics of full-scale measurement and wind tunnel test

带挑檐双坡屋面低矮房屋刚性模型的风洞试验在湖南大学风洞试验室中进行[19]，模型的几何缩尺比为1∶50，模型的尺寸为490 mm(长)×190 mm(宽)×88 mm(高)，挑檐外伸长度为26 mm，厚度为5 mm，阻塞率小于1%，满足风洞试验要求。根据低矮实测房[12,18]在台风“莎莉嘉”和“彩虹”登陆期间的现场实测风场结果，考虑不同风向角地貌不同，在风洞试验中通过改变尖劈和粗糙元等模拟了三种来流条件，地貌粗糙度分别为0.03 m、0.087 m、0.03 m。平均风速和湍流度剖面根据《建筑结构荷载规范》(GB 50009-2012)[25]如下式所示：

式中：U10和I10分别为离地面10 m 高度处的平均风速和湍流强度；U(z)和I(z) 分别为z高度处的平均风速和湍流强度； α为指数律大小。三种来流条件下的 α值分别为0.15、0.19、0.22，参考高度处(风洞试验中距底面0.2 m 即实测中离地10 m 高度)的平均风速及三个风向的湍流强度见表1，风速采样频率为500 Hz。基于低矮房屋的特征长度及参考高度处平均风速得到风洞试验雷诺数为Re=2.59×105。刚性模型表面共布置了399 个测点，挑檐处上下表面共布置了104 个测点，并在模型角部区域进行加密，如图2 所示。模型表面风压使用PSI 高频同步压力扫描阀系统(Synchronous multi-pressure sensing system, SMPSS)，采样频率为312.5 Hz，采样时长为120 s，相当于实测中3 个10 min 的采样长度。更详细的风洞试验信息可参考文献[19]。

1.2 LES 数值模拟

1.2.1 控制方程

大涡模拟方法基本思想是在数值模拟中利用特征网格尺寸对涡旋进行过滤，直接求解N-S 方程中大于空间过滤网格的涡旋运动，同时通过亚格子模型模拟小于网格尺度的涡旋运动[26]。空间滤波后的不可压缩流动的大涡模拟的控制方程如下所示：

1.2.2 计算域及网格划分

数值模拟计算域为15L(长)×5L(宽)×6H(高)，模型位于参考坐标的中心，模型距入流边界长度为5L，距出流边界长度为10L，其中，L为建筑模型长度，B为建筑模型宽度，H为建筑模型高度，如图3 所示，数值模拟中模型阻塞率约为3.3%<5%，满足计算风工程的要求[27]。

图3 计算域及边界条件Fig. 3 Computational domain and boundary conditions

网格划分采用结构化网格，其中近壁面区域为低雷诺数流动，为了准确地捕捉建筑物绕流流场的复杂湍流特性，对建筑物壁面网格进行加密处理。建筑物近壁区首层网格高度为 1×10-4m，其第一层网格节点位于粘性子层内，对应的y+值小于5。在屋面迎风前缘、屋脊处及建筑结构尾流区等风速梯度较大区域，应使相邻网格尺寸相近，减少数值截断误差，因此，在建筑附近设定网格加密区域，网格增长率设为1.05。加密区域为距模型迎风面1.0H，距建筑两侧面各1.0H，距模型屋面1.0H，距模型背风面2.0H。加密区外侧的网格增长率不超过1.1，如图4 所示，网格总量为 5 .4×106。

图4 数值模拟网格划分策略Fig. 4 Grid meshing scheme in the numerical simulation

为验证数值结果的网格无关性，基于此基础网格(网格总数为 5.4×106)，建立了两套不同尺寸的网格(稀疏网格首层尺度为4 ×10-4m，网格总数为2 .6×106；加密网格首层网格尺寸为0 .5×10-4m，网格总数为 8 .9×106)，采用GCI(Grid Convergence Index)指数法进行网格无关性验证[28]，量化因网格疏密变化所造成的数值误差。由于篇幅原因，仅给出0o风向角下提取的屋面迎风前缘分离处的风压作为参考量fi，结果分析见表2。可以发现，不同网格之间的模拟结果存在差异，且随着网格量的增加，不同网格计算结果之间的误差会逐渐缩小。其中，基础网格计算结果与加密网格计算结果之间的相对误差3% 以内，满足计算精度要求。综合考虑精度和效率的要求，选取基础网格进行后续数值模拟。

表2 网格无关性分析Table 2 Grid-convergence analysis

1.2.3 边界条件

边界条件设定如表3 所示，入流面采用速度入口；计算域两侧及顶部为对称边界(Symmetry)；计算域出口为自由出流(Outflow)；计算域底部及模型表面采用无滑移壁面(No-slip wall)。

表3 边界条件设定Table 3 Setting-ups of boundary conditions

1.2.4 入口湍流生成及其自保持性验证

生成能够准确模拟来流风场特性的入口湍流是基于LES 模型研究结构风效应的关键问题之一。目前大涡模拟中的入口湍流生成方法主要分为两类：预前模拟法和人工合成法。周桐等[29-30]探究了不同大涡模拟入口湍流方法的基本原理，特点及适用性。预前模拟法可以模拟相对真实的流场结构，并且湍流特性在计算域内具有良好保持性，计算容易收敛，但是无法直接定义目标湍流特性，调试过程复杂，而且网格量多，计算效率低。人工合成法基于严格的数理推导，构造入口边界条件满足大气边界层风场特性，且其计算效率高。本文选取CDRFG (Consistent discrete random inflow generation)方法来模拟大涡入口湍流生成[31]。基本思想是将三维能谱表示为一系列离散谱的线性叠加，对于每个离散谱，采用Kraichnan[32]方法生成对应的随机脉动速度场，进而合成满足三维能量谱的脉动速度场。

采用CDRFG 能够生成满足来流风场统计特性的入口湍流边界条件，且满足连续方程无散化的要求，但是其无法完全严格满足N-S 方程，LES自身的亚格子湍流模型无法真实模拟小于过滤网格的小尺度涡旋运动，入口湍流特性可能沿计算域顺流向改变，从而导致目标处与入口处湍流特性无法保持一致。为验证入口处和建筑物处的湍流特性保持一致，并确保数值模拟中来流条件与风洞试验来流的一致性，建立空风场进行CDRFG方法的验证。空风场的计算域尺寸与有建筑物的计算域尺寸一致，求解方法设定如1.2.5 节介绍。地面粗糙为0.03 m 来流条件下的自保持性验证结果如图5 所示，图5(a)表明该方法生成的平均风速和湍流度剖面自保持性较好，且和风洞试验结果基本一致。图5(b)为参考高度处的无量纲风速功率谱，在折减频率大于5 时，风速功率谱密度出现较明显下降趋势，这是由于顺风向网格的亚格子模型过滤效应导致，与网格分辨率有关[33]。低矮房屋的结构特征频率低于来流截断频率，且在折减频率低于5.0 的风速谱和目标Karman 谱及风洞试验风速谱吻合较好，表明CDRFG 方法生成的入口湍流是准确的且满足自保持性。

图5 LES 模拟来流条件对比验证Fig. 5 Upstream wind conditions in the wind tunnel test and numerical simulations

1.2.5 求解算法设定

本文数值模拟工作依托广东超算中心(Intel Xeon E5-2692，内存128 G)，采用72 核并行计算。基于通用流体力学软件ANSYS Fluent 19.0，通过自编并行化UDF(User defined function)子模块将CDRFG方法植入，生成LES 模拟的来流湍流。非线性对流项采用二阶迎风格式(Second order upwind)进行离散，动量方程采用有界中心差分格式(Bounded central differencing)，时间离散为二阶全隐格式。对于速度压力耦合方程采用SIMPLE (Semi-implicit method for pressure-linked equations)法进行求解。为加速LES 模拟中的湍流流场发展以及提高收敛速度，先采用RNGk-ε (Renormalization groupk-ε)湍流模型对流场进行定常模拟，对定常流场结构进行瞬态化处理作为大涡模拟的初始条件[34]。为进一步提高大涡模拟的准确性，设定时间步长Δt=0.0001 s ，对应的库朗数CFL＜1.0。将参考高度的风速从入口流至出口穿过计算域的时间成为一个全流域时间(Flow-through time)，模拟了30个全流域时间，为保证统计结果的稳定性，提取后面24 个全流域时间的结果进行统计分析。

基于现场实测和风洞试验的三种不同来流条件，分别对0°、180°及225°风向角下低矮房屋的风荷载特性进行了数值模拟研究。

2 结果分析与讨论

数值模拟结果用风压系数表示，其定义与现场实测和风洞试验中的数据分析相同。平均风压系数Cp,mean、脉动风压系数Cp,rms及极值风压系数Cp,min如下所示：

式中：pref为参考静压，即在风洞试验中连通外界大气压作为参考静压； ρ为空气密度；Uref为参考高度处的平均风速，选取低矮房屋平均屋面高度处的风速作为参考风速；p¯为采样周期内得到的平均风压； σp为脉动风压均方根值；pˇ测量样本中风压的最小值。其中对于挑檐部分由于上下表面同时存在压力，因此，挑檐部分的净压力为：

2.1 基于现场实测的LES 数值模拟验证

在现场实测中，测量得到0°风向角的数据较充分，故选取0°风向角的结果进行现场实测和LES 数值模拟的对比验证。图6 为0°风向角时数值模拟和现场实测及风洞试验在屋面24 个不同位置测点处的风压系数对比。结果表明：LES 模拟结果和风洞试验及实测结果吻合较好；在分离前缘及屋脊位置处(对应图中测点A 列和F 列)，发生明显的流动分离现象，在该区域产生较大的风压系数(绝对值，下同)，该风压分布特征与低矮房屋屋面通常在屋檐及屋脊区域发生局部破坏的现象相符。图6(a)中平均风压系数在分离(对应测点A 列)和屋脊线前缘位置处(对应测点F 列)，风洞试验和LES 模拟结果相较于现场实测结果偏大；由图6(b)可知，脉动风压系数在分离处(对应测点A 列)LES 模拟和风洞试验相比于实测结果偏小；由图6(c)可知，极值风压系数分布规律与平均分压系数相似，在分离及屋脊线位置处，风洞试验和LES 模拟在一定程度上低估了极值风压系数。

图6 0°风向角下风压系数对比结果Fig. 6 Comparison of the pressure coefficients in the wind direction θ of 0°

挑檐是低矮房屋风致易损区域，在台风作用下其上、下两个表面同时受风荷载作用。选取测点K1 和J2，分析了挑檐位置处的净压力系数(包含平均、脉动及极值净风压系数)随风向角变化情况，如图7 所示。由图7 可知，三种不同研究方法下，测点K1 和J2 净风压系数随风向角变化趋势基本一致。当风向角为240°～300°时，测点K1和J2 位于流动分离区域，数值模拟风压结果和风洞试验基本一致，但两者的净极值风压系数与实测结果存在明显差异。可能原因有两方面：一方面受雷诺数效应的影响(现场实测雷诺数为4.07×107，为LES 数值模拟和风洞试验的125 倍)，根据Cheung 等[15]关于低矮房屋表面风压特性研究发现对其表面风压特性雷诺数效应显著。另一方面，风压谱频率在大于折减频率(f H/U≈0.7)的能量主要是由锥形涡所引起的，即由建筑物引起的特征湍流[35]；Holmes[36]研究发现特征湍流对于流动再附有促进作用，从而影响建筑物表面的极值风压；而在数值模拟和风洞试验中不能完全模拟现场实测中大气湍流在整个频域范围内的能量级串过程，这可能是导致数值模拟和风洞试验与现场实测在测点K1 和测点J2 位置处的极值风压差异。

图7 不同风向角下屋檐测点K1 和J2 的风压系数Fig. 7 Pressure coefficient at the pressure taps K1 and J2 on the roof overhang under different wind directions

2.2 基于风洞试验的LES 数值模拟验证

本节主要基于模拟台风风场的风洞试验结果，对比验证并量化分析了LES 数值模拟在模拟台风高湍流风场下的适用性。受篇幅限制，针对低矮房屋单侧挑檐迎风的典型工况，主要选取正风向180°和斜风向225°两个风向角下的结果。

图8 对比了180°和225°风向角下LES 模拟及风洞试验的低矮房屋的平均风压系数、脉动风压系数及极值风压系数分布。通过对比发现LES 模拟结果与试验分布具有良好一致性。图8(a)为风向角180°的平均风压系数分布图，迎风面挑檐及屋脊附近有较大的流动分离，吸力较大，且挑檐处风压系数为最大值，平均风压系数在屋脊两侧附近呈对称分布；背风面风压系数呈阶梯状分布，其绝对值由屋脊处向屋檐处逐渐减小。在迎风面挑檐到屋脊处范围内LES 结果比试验值偏小，而屋脊线至屋檐处LES 结果比试验偏大。225°斜风向角下的平均风压系数如图8(b)所示，在模型两侧迎风前缘及脊线两边区域出现瓣状强吸力区。屋面在斜风向角下其屋面迎风角两侧及屋脊线位置处发生明显的流动分离形成锥形涡，在屋面迎风面较长一侧受柱形涡影响更加显著，从而导致在该侧LES 模拟的风压值比试验值偏大。180°和225°风向角下的屋面脉动风压系数与平均风压系数分布类似。图8(c)中在180°风向角下，迎风面挑檐位置出现强脉动吸力，在屋脊处的脉动吸力也较大，但背风面区域的脉动风压系数较风洞试验值偏大。图8(d)中225°风向角下，强脉动吸力出现在迎风面角点的两个豆瓣状区域内，与平均风压系数分布相似，在迎风面较长一侧的模拟值比试验值偏大。风向角为180°时，极小值风压系数的分布如图8(e)所示，风洞试验与LES 模拟的极小值风压系数在挑檐处分布基本保持一致，LES 模拟的极值风压系数在屋脊及背风面区域分布比风洞试验结果偏小，从挑檐处沿着顺流向风向逐渐减小，而风洞试验的极值风压系数与平均风压系数类似，在屋脊处有较大值。图8(f)为风向角225°的极小值风压系数分布图，分布形状与平均风压系数分布相同，其绝对值的最大极小值风压系数出现在屋面迎风面角点两侧。LES结果和风洞试验的风压特性差异的可能原因是：风洞试验因尺寸的限制不能真实的模拟低频区大尺度漩涡能量，而LES 数值模拟由于亚格子湍流模型的过滤效应不能有效模拟高频区小尺度涡旋能量。

图8 180 °和225°风向角下屋面风压系数云图对比Fig. 8 Comparison of contour of the mean pressure coefficient in the wind directions θ of 180° and 225°

图9 和表4 为45°风向角和180°风向角下LES模拟与风洞试验风压系数的误差量化分析，主要考虑了 ± 10% 、 ±20% 和 ± 30%三类置信区间。整体来看，LES 数值模拟的屋面风压系数和风洞试验结果基本一致性，包括平均、脉动和极值风压在内的结果置信区间在± 30%以内所占的比例达到85%以上。同时，平均风压系数(一阶统计量)的置信区间模拟精度要大于脉动及极值风压系数(高阶统计量)，且误差范围越小，模拟精度差别越大。

表4 不同风向角下LES 与风洞试验结果误差分析Table 4 Error analysis of pressure coefficients between LES simulation and the wind tunnel test

图9 180°和225°风向角下LES 和试验误差分析Fig. 9 Error analysis of pressure coefficients obtained from LES and wind tunnel tests in the wind direction θ of 180° and 225°

2.3 低矮建筑绕流瞬态流场结构

本节基于Q准则对带挑檐双坡屋面低矮房屋表面的流场结构进行识别。Q准则是速度梯度张量的二次不变量，其定义为[37]：

当Q＞0 时，相比流体的应变率 (SijSi j)，转动速率 (ΩijΩi j)占主导，即流场中涡旋结构占主导地位。图10 给出180°和225°风向角下建筑物表面的Q等值面云图(Q=6.0×105s-2)，并采用压力系数对其进行着色来分析不同风向角下带挑檐双坡屋面低矮房屋模型表面的流场结构及其对风压分布特性的影响机理。

如图10 所示，标准Smagorinsky 亚格子模型能解析流场中小尺度的涡结构，不同风向角作用下，低矮房屋模型前缘由于剪切应力的作用，在模型前缘位置处形成分离旋涡。同时由于逆压梯度的作用，模型屋面及两侧发生分离形成较大的分离旋涡导致该区域出现较大的负压力区。随着剪切层向下游流动，分离区扩大而旋涡强度明显减弱。180°风向角作用下，屋面前缘及两侧前缘部分形成柱形的分离旋涡；而225°斜风向角下作用下，屋面迎风面两侧形成锥形及柱形的分离旋涡。与图8 中的风压系数分布对比，即分离旋涡对应的区域存在较大风压值。180°风向角作用下，外部剪切层流速较大，由于低频脉动旋涡停留较长时间，所以出现极值吸力，即对应平均风压系数绝对值的最大值出现在挑檐位置，与图8(a)相对应；随着来流顺方向发展达到背风面时，由于较大的黏性应力和剪切变形，旋涡脱落分解成大量的小尺度涡，湍流能量耗散较快，脉动风压系数减小，与图8(c)相对应。斜风向角作用下在分离区存在更大的风压值，其可能原因是因为斜风向作用下由于分离区形成锥形和柱形的分离旋涡，其流场结构更加复杂形成更大的逆压力梯度，从而导致斜风向角下分离区的出现更大的负压力，结果和图8(b)一致。图8 中风压系数分布与图10流场结构相结合可以发现，迎风挑檐会造成屋面前缘流动分离提前发生，但对迎风前缘屋面风压分布规律影响较小，挑檐下缘形成的分离泡产生较大脉动吸力，挑檐局部净风压系数未显著增大。

图10 基于 Q准则的不同风向角下涡量等值面云图Fig. 10 The iso-surface of the turbulent flow fields around the low-rise building based on Q criterion in different wind directions

3 结论

本文基于“莎莉嘉”和“彩虹”期间带挑檐低矮双坡房屋的现场实测及风洞试验，对带挑檐低矮双坡房屋的LES 模拟适用性进行了研究。主要结论如下：

(1)通过与现场实测和风洞试验对比，验证了采用CDRFG 湍流人工合成方法能够生成满足台风风场统计特性的入口湍流边界条件；同时也验证了基于LES 方法模拟台风风场下低矮房屋风荷载统计量化和空间分布规律的有效性。

(2)与现场实测和风洞试验结果相比，在不同风向角下，带挑檐双坡屋面低矮房屋的LES 模拟结果得到的平均、脉动和极值风压系数在30%置信区间的模拟精度达85%以上。

(3)在225°斜风向角下，在模型两侧迎风前缘及脊线两边区域出现风压系数最大值；在180°风向角下，迎风面挑檐及屋脊附近有较大的流动分离，吸力较大，且挑檐处风压系数为最大值，背风面风压系数绝对值沿顺流向逐渐减小。

(4)迎风挑檐会造成屋面前缘流动分离提前发生，但对迎风前缘屋面风压分布规律影响较小，挑檐下缘形成的分离泡产生较大脉动吸力，挑檐局部净风压系数未显著增大。